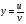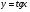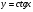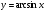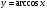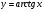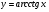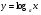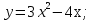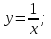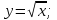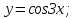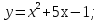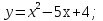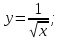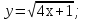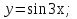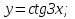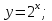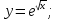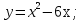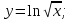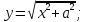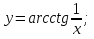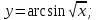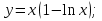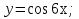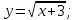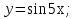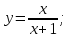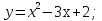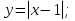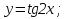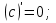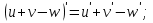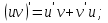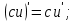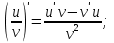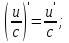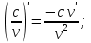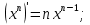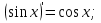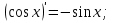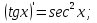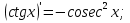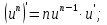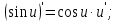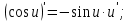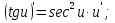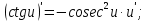Алашы функция жне аныталмаан интеграл
 Скачать 356.63 Kb. Скачать 356.63 Kb.
|
|
Трансценденттік функцияларды интегралдау Трансценденттік рационал функцияларды интегралдау келесі түрдегі интегралдарды есептеуге келеді, мұнда R –рационал функция:
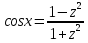 , , 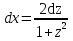 . .
Мысал. 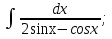 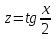 деп алып, жоғарыдағы алмастыруларды енгіземіз. деп алып, жоғарыдағы алмастыруларды енгіземіз. 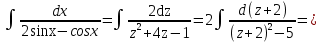 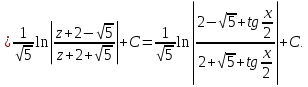 Тапсырмалар:
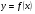 функциясы берілсін. Мұндағы, х – тәуелсіз айнымалы (аргумент), у – тәуелді айнымалы (функция). функциясы берілсін. Мұндағы, х – тәуелсіз айнымалы (аргумент), у – тәуелді айнымалы (функция). 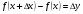 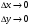 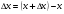 Мысал 1. 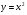 функцияның өсімшесін табыңыз. функцияның өсімшесін табыңыз.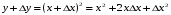 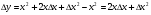 Мысал 2. 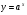 функцияның өсімшесін табыңыз. функцияның өсімшесін табыңыз.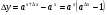 Анықтама. 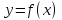 функциясының туындысы деп функциясының туындысы деп 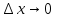 ұмтылған кезде осы функцияның ұмтылған кезде осы функцияның 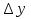 өсімшесі сәйкесінше тәуелсіз айнымалының өсімшесі сәйкесінше тәуелсіз айнымалының 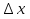 өсімшесіне қатынасының шегін айтамыз: өсімшесіне қатынасының шегін айтамыз: 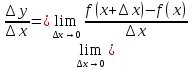 Туынды келесідей белгіленеді: 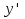 немесе немесе 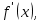 немесе немесе 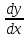 . . Туынды табу амалы дифференциалдау деп аталады. Көптеген жерде туынды табу формулалары беріледі, бұл әдістемелік құралда сол элементар функциялардың туындысын табу жолын келтірейік:
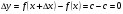 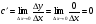
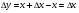  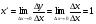
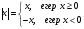 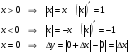 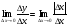 шегі анықталмайды. Демек, шегі анықталмайды. Демек,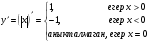
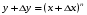 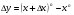 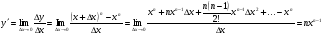
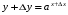 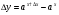 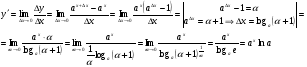
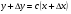 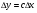 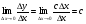 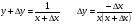 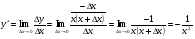
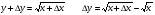 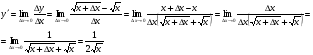
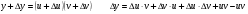 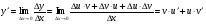 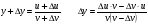 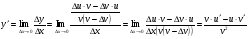
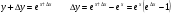 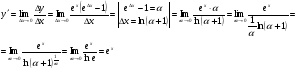
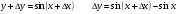 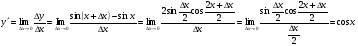 себебі, тамаша шек бойынша себебі, тамаша шек бойынша 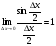 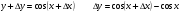 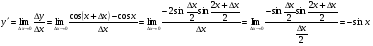 себебі, тамаша шек бойынша 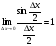 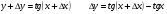 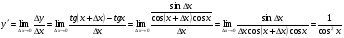 Себебі, тамаша шек бойынша 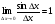 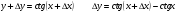 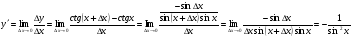 себебі, тамаша шек бойынша себебі, тамаша шек бойынша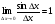 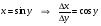 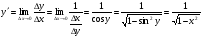 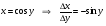 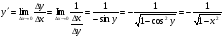 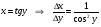 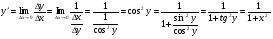  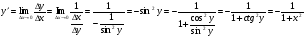 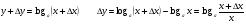 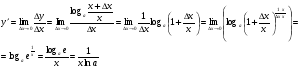 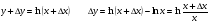 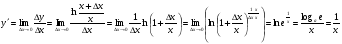 Тапсырмалар:
Анықтама. 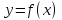 функциясының туындысы деп функциясының туындысы деп 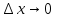 ұмтылған кезде осы функцияның ұмтылған кезде осы функцияның 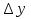 өсімшесі сәйкесінше тәуелсіз айнымалының өсімшесі сәйкесінше тәуелсіз айнымалының 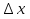 өсімшесіне қатынасының шегін айтамыз: өсімшесіне қатынасының шегін айтамыз: 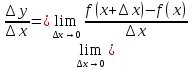 Туынды келесідей белгіленеді: 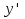 немесе немесе 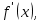 немесе немесе 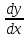 . . Туынды табу амалы дифференциалдау деп аталады. Жоғарыда көрсеткендей функцияның туындысын табу үшін функция өсімшесінің аргумент өсімшесіне қатынасынын шегін таба беру қиындыққа әкеледі. Сондықтан тек келесі кестеге сүйене отырып, таба салуғада болады:
Егер функция күрделі функция болса, онда ол келесідей болады:
Енді n – ретті туынды алу жолдарын көрсетейік. 1)  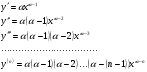 2) 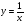 n–ретті туындысын табайық. n–ретті туындысын табайық.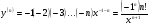 3) 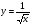 n–ретті туындысын табайық. n–ретті туындысын табайық.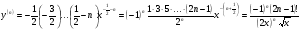 4) 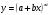 n–ретті туындысын табайық. n–ретті туындысын табайық.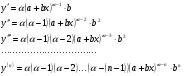 5) 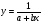 n–ретті туындысын табайық. n–ретті туындысын табайық.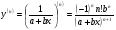 6) 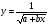 n–ретті туындысын табайық. n–ретті туындысын табайық.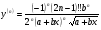 7) 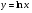 n–ретті туындысын табайық. n–ретті туындысын табайық.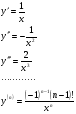 8) 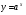 n–ретті туындысын табайық. n–ретті туындысын табайық.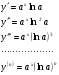 9) 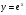 n–ретті туындысын табайық. n–ретті туындысын табайық.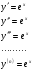 10) 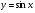 n–ретті туындысын табайық. n–ретті туындысын табайық.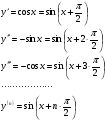 Мысалы: n=50 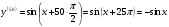 11) 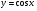 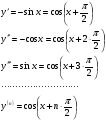 12) 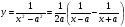 n–ретті туындысын табайық. n–ретті туындысын табайық.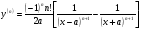 13) 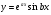 n–ретті туындысын табайық. n–ретті туындысын табайық.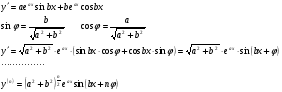 14) 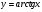 n–ретті туындысын табайық. n–ретті туындысын табайық.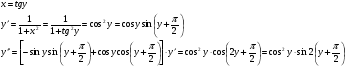 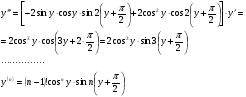 Егер 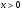 болғанда болғанда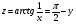 Бұрышын енгізсек, онда бұл формуланы төмендегіше қайталап жазуға болады. 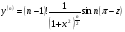 немесе немесе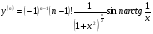 15) 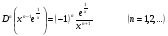 дәлелдеу керек. дәлелдеу керек.N=1 үшін 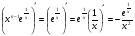 орындалады орындаладыn=2 үшін 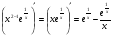 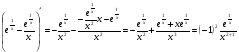 орындалады орындаладыn-үшін дұрыс деп ұйғарып, n+1 үшін дәлелдейік 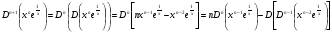 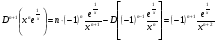 яғни, n+1 үшін орындалады екен. 16) 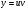 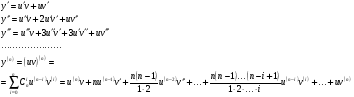 Мысалы: 1) 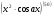 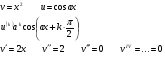 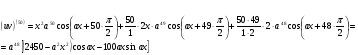 2) 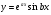 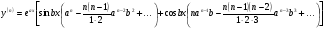 |

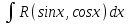 мұндай түрдегі интегралдарды интегралдау үшін
мұндай түрдегі интегралдарды интегралдау үшін 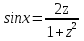 ,
,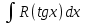 , мұнда
, мұнда 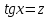 алмастыруын енгіземіз. Сонымен қатар,
алмастыруын енгіземіз. Сонымен қатар, 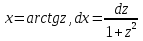 .
.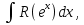 мұнда
мұнда 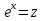 алмастыруын енгіземіз. Сонымен қатар,
алмастыруын енгіземіз. Сонымен қатар, 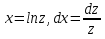 .
.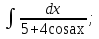
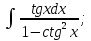
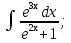
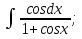
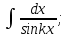
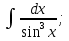
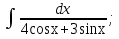
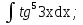
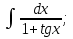
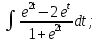
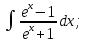
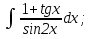
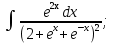
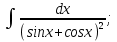
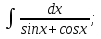
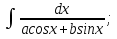
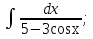
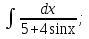
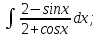
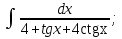
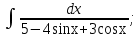
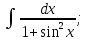
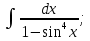
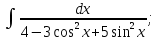
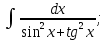
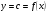 тұрақтының туындысын табу жолы:
тұрақтының туындысын табу жолы: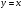 туындысын табу жолы:
туындысын табу жолы: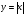 модулді функцияның туындысын табу жолы:
модулді функцияның туындысын табу жолы: 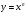 дәрежелік функцияның туындысын табу жолы:
дәрежелік функцияның туындысын табу жолы: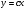 туындысын табу жолы:
туындысын табу жолы: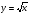 туындысын табу жолы:
туындысын табу жолы: