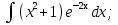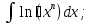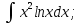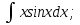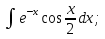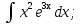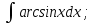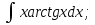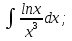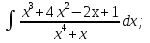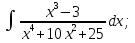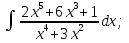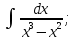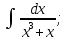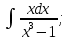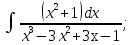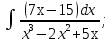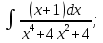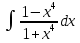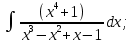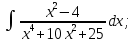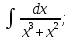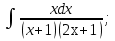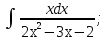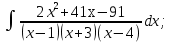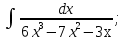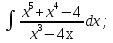Алашы функция жне аныталмаан интеграл
 Скачать 356.63 Kb. Скачать 356.63 Kb.
|
Өзінің дифференциалына қарап 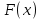 функциясын іздеу, яғни дифференциалдауға кері амалын интегралдау деп атаймыз, ал ізделінді функциясын іздеу, яғни дифференциалдауға кері амалын интегралдау деп атаймыз, ал ізделінді 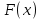 функциясын функциясын 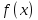 функциясының алғашқы функциясы деп аталынады. функциясының алғашқы функциясы деп аталынады. Кез келген үзіліссіз 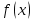 функциясының бір-бірінен тек тұрақты санға ғана ерекшеленетін көптеген әртүрлі алғашқы функциялары бар болады. Егер функциясының бір-бірінен тек тұрақты санға ғана ерекшеленетін көптеген әртүрлі алғашқы функциялары бар болады. Егер 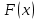 функциясы функциясы 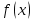 функциясының алғашқы функциясы болса, яғни егер функциясының алғашқы функциясы болса, яғни егер 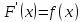 болса, онда болса, онда 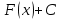 да алғашқы функция болады, мұнда да алғашқы функция болады, мұнда 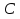 -кез келген тұрақты сан. Немесе -кез келген тұрақты сан. Немесе 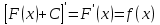 болады. болады. 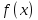 функциясының барлық алғашқы функцияларының жиыны жалпы функциясының барлық алғашқы функцияларының жиыны жалпы 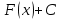 өрнегі осы функцияның анықталмаған интегралы деп аталады және өрнегі осы функцияның анықталмаған интегралы деп аталады және 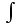 белгісімен белгіленеді: белгісімен белгіленеді: 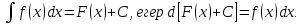 Анықталмаған интегралдардың кейбір қасиеттері.
Интегралдаудың негізгі формулалары: Мысал. 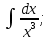 Шешуі: 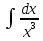 = =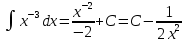 ; ;Тексеру: туындысын алып, функцияның дұрыс интегралданғанын тексереміз. 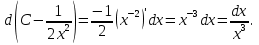 Мысал. 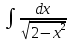 ; ;Шешуі: 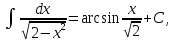 10-ші формуланы қолданып шығардық. Тексеру: 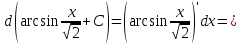 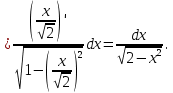 Мысал. 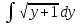 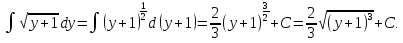 Тексеру: 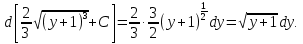 Тапсырмалар:
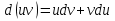 осы көбейтудің дифференциалының формуласын екі жағын интегралдап, келесі бөліктеп интегралдау формуласын аламыз: осы көбейтудің дифференциалының формуласын екі жағын интегралдап, келесі бөліктеп интегралдау формуласын аламыз: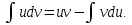 Бұл формулада 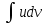 интегралын зерттеуде мына интегралын зерттеуде мына 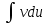 интегралды есептеуге келеді. Мұнда бастапқы интегралды есептеу соңғы интегралды есептеуден қиынырақ болғандықтан осы формуланы пайдаланып шығарамыз. интегралды есептеуге келеді. Мұнда бастапқы интегралды есептеу соңғы интегралды есептеуден қиынырақ болғандықтан осы формуланы пайдаланып шығарамыз. 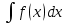 интегралын есептеу үшін интеграл астындағы өрнекті u және dv деп белгілеп алу керек. dv ретінде көбінесе туынды алынбайтын функцияларды аламыз, мысалы үшін интегралын есептеу үшін интеграл астындағы өрнекті u және dv деп белгілеп алу керек. dv ретінде көбінесе туынды алынбайтын функцияларды аламыз, мысалы үшін 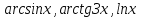 . . Мысал. 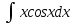 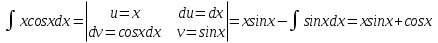 Тапсырмалар:
Рационал функциялар әрқашанда элементар функцияларда интегралданады. 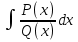 , мұнда , мұнда 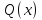 және P(x) көпмүшелер, бөлшекті рационал функцияның интегралын барлық уақытта интегралдауға болатын қосылғыштарға жіктеу арқылы табуға болады. және P(x) көпмүшелер, бөлшекті рационал функцияның интегралын барлық уақытта интегралдауға болатын қосылғыштарға жіктеу арқылы табуға болады. Алымының дәрежесі бөлімінің дәрежесінен үлкен не тең болатын бұрыс рационал бөлшекті алымын бөліміне бөлу арқылы, яғни көпмүшелер мен алымының дәрежесі бөлімінің дәрежесінен кіші болатын дұрыс бөлшектін қосындысы түрінде жазуға болады. Дұрыс рационал бөлшекті әрқашанда келесі екі интегралданатын бөлшектің қосындысы түрінде элементар бөлшектерге жіктеуге болады: 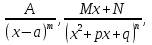 мұнда m және n–бүтін оң сан.
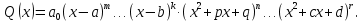 б) Берілген бөлшекті келесідей түрде элементар бөлшектердің қосындысы түрінде жіктей аламыз: 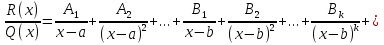 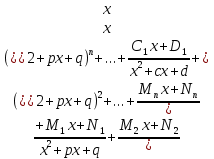 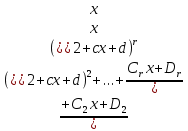 мұнда 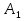 ,…, ,…, 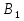 ,…, ,…, 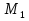 ,…, ,…, 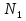 ,…, ,…, 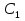 ,…, ,…, 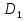 ,..., -кейбір тұрақтылар. Бұл тәсілде бөлшектің бөліміндегі көбейткіштердің дәрежесіне байланысты сонша элементар бөлшектердің қосындысы түрінде жазылады. Ал бөлшектің алымы бөлімінің сызықты не квадратты функция болатындығына сәйкес тұрақты не сызықты функция болады. ,..., -кейбір тұрақтылар. Бұл тәсілде бөлшектің бөліміндегі көбейткіштердің дәрежесіне байланысты сонша элементар бөлшектердің қосындысы түрінде жазылады. Ал бөлшектің алымы бөлімінің сызықты не квадратты функция болатындығына сәйкес тұрақты не сызықты функция болады. в) Теңдіктің екі бетінде 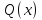 -ке көбейтіп, бөлшек бөлімінен құтыламыз. -ке көбейтіп, бөлшек бөлімінен құтыламыз. г) Енді алымдарының теңдігінен коэффициенттерін теңестіріп, теңдеулер жүйесін аламыз. д) Жүйені шешіп, табылған коэффициенттерді элементар бөлшектердің қосындысына апарып қоямыз. Осы алынған элементар бөлшектерді интегралдаймыз. Яғни кез келген дұрыс рационал бөлшекті интегралдауда элементар бөлшектердің қосындысына жіктеуден кейін келесі түрдегі интегралдарды табу керек болады: 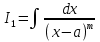 және және 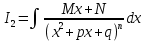 . .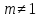 кезде кезде 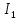 интегралы келесідей шығады: интегралы келесідей шығады: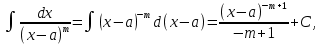 Енді мысал көрсетейік. Мысал. 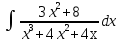 а) Бөлшектің бөлімін қарапайым көбейткіштерге жіктейміз: 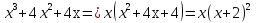 ; ;б) интеграл астындағы бөлшекті элементар бөлшектердің қосындысы түрінде жазайық: 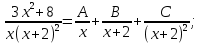 в) теңдіктің екі жағынада 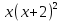 көбейтіп, бөлшектің бөлімінен құтыламыз: көбейтіп, бөлшектің бөлімінен құтыламыз: 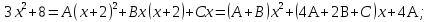 г) теңдіктің коэффициенттерін теңестіріп, теңдеулер жүйесін аламыз: 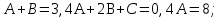 д) осы жүйені шеше отырып, біз коэффициенттерді табамыз: 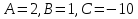 . Бұдан . Бұдан 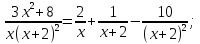 Енді интегралдаймыз: 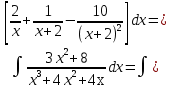 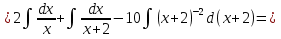 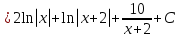 Тапсырмалар:
|

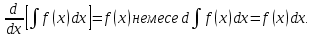
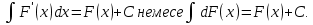
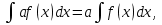 яғни тұрақты көбейткішті интеграл белгісінің алдына шығаруға болады.
яғни тұрақты көбейткішті интеграл белгісінің алдына шығаруға болады.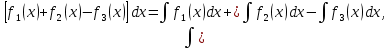 яғни қосындылардың интегралы барлық қосылғыштардың интегралдарының қосындысына тең.
яғни қосындылардың интегралы барлық қосылғыштардың интегралдарының қосындысына тең. 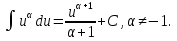
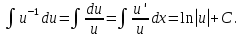
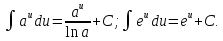
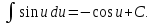
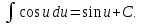
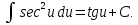
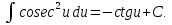
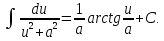
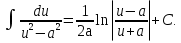
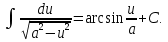
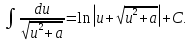
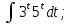
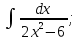
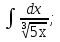
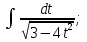
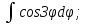
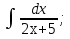
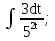
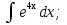
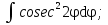
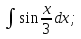
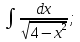
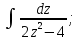
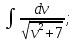
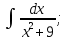
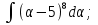
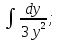
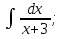
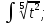
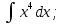
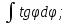
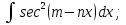
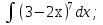
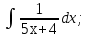
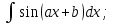
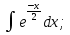
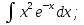
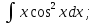
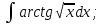
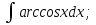
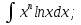
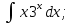
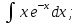
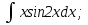
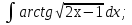
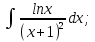
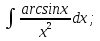
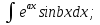
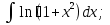
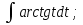
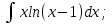
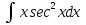 ;
;