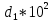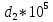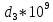Термодинамика. Аналитический аппарат равновесной термодинамики
 Скачать 70.08 Kb. Скачать 70.08 Kb.
|
|
Аналитический аппарат равновесной термодинамики. Объект и методы исследования. Постулаты о равновесии и транзитивности равновесия, следствия этих положений. I-ый и II-ый законы равновесной термодинамики как постулаты существования внутренней энергии и энтропии – функций состояния макросистем. Теорема Нернста. Математические записи этих положений в общей форме для открытых и закрытых систем, их практические следствия. Понятие о превратимой (доступной) и балластной части внутренней энергии. Работа как безэнтропийная форма энергообмена. Термодинамические функции и функционалы. Характеристики функции и их свойства. Структура дифференциальных уравнений для систем с двумя независимыми переменными. Основные задачи, решаемые методом равновесной термодинамики. Семинар №1-2 Расчётное соотношение внутренней энергии неидеального газа и его вывод. U(T,V) = Uид(T) + ΔUттеор [кДж/кмоль] (1.1) где ΔUттеор – изотермическое отклонение, которое учитывает отклонение от идеальногазовой модели (МИГ) Уравнение внутренней энергии идеального газа Uид(T) = U˚(To) + 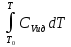 , (1.2) , (1.2)где To – точки отсчета внутренней энергии(стандартное состояние) To = 273,15K Внутренняя энергия идеального газа является функцией только температуры «Т» и не зависит от объёма, занимаемого газом (1.3). 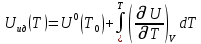 (1.3) (1.3)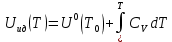 , ,где 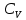 – изохорная теплоёмкость идеального газа. – изохорная теплоёмкость идеального газа.Если газ является калорически совершенным, то теплоёмкость газа не зависит от температуры, а определяется числом степеней свободы газа: 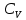 = = 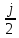 RmT, где j= RmT, где j= Приведём пример: j=3 для одноатомных газов (He, Ar); j=5 для двухатомных одноимённых и разноимённых газов (N2, NO); j=7 для трёх и более атомов, а также для смеси любых, в том числе одноатомных газов (классический пример воздух). Реальные газы и их смеси учитывают зависимость внутренней энергии от объёма, ими занимаемого: 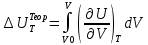 (1.4), где (1.4), гдеΔUттеор – теоритическое изотермическое отклонение, которое учитывает отклонение от идеальногазовой модели (МИГ) На основание объединённого уравнения 1-го и 2-го начала равновесной термодинамики ,а также уравнения Максвелла(в качестве термодинамического потенциала выступает энергия А(V,T) Гиббса-Гельмгольца (1.5). TdS = dU + pdV (1.5) 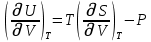 Из уравнения Максвелла для изохорно-изотермического потенциала имеем:  (1.6) (1.6)Подставим данное соотношение и получим (1.7):  (1.7) (1.7)Из уравнения Ван-дер-Ваальса выведем:  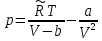 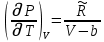 Откуда следует: 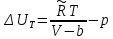 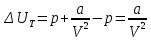 Подставим в уравнение (1.4) 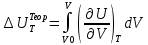 : :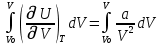 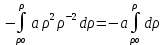 Т.к. 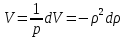 Таким образом уравнение внутренней энергии неидеального газа имеет вид: 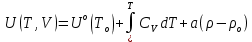 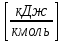 Полученное выражение позволяет сделать вывод о влияние на величину внутренней энергии объёма, занимаемого газом. Полученное выражение позволяет сделать вывод о влияние на величину внутренней энергии объёма, занимаемого газом. Термическое уравнение состояния (виды и способы получения). Уравнение Ван-дер-Ваальса Уравнение Ван-дер-Ваальса уже является уравнением неидеального газа, в будущем будем именовать «реального» газа (МРГ). В неидеальных, т.е. реальных, газах в отличие от идеальных газов существенны силы межмолекулярных взаимодействий, силы притяжения, когда молекулы находятся на значительном расстоянии, и сила отталкивания при достаточном сближении их друг с другом, нельзя пренебречь собственным объемом молекул. Уравнение Ван-дер-Ваальса: (p + 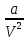 ) * (V-b) = RmT, где (1.1) ) * (V-b) = RmT, где (1.1)Pмол = 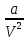 – давление (молекулярное), или внутреннее давление молекул газа, где – давление (молекулярное), или внутреннее давление молекул газа, где а – коэффициент пропорциональности, зависящий от природы газа a = 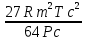 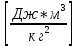 b = b = 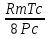 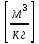 Tc, К – критическая температура, это такое значение температуры, при которой свойства газовой и жидкой фазы тождественны. Это критическая температура; постоянная справочная величина, соответствующая значению температуры и давления, при которых все свойства газовой и жидкой фазы становятся тождественны. Критическая температура Tc соответствует такому значению температуры, выше которой газ невозможно перевести в жидкое состояние, увеличивая давление. Наличие межмолекулярных сил отталкивания приводит к тому, что молекулы могут сближаться между собой только до некоторого минимального расстояния. Поэтому можно считать, что свободный для движения молекул объем будет равен V-b, где b – тот минимальный объем, до которого можно сжать газ, 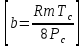 . .Поскольку длина свободного пробега молекул уменьшается, число ударов о стенку в единицу времени увеличивается, а, следовательно, и давление возрастает по сравнению с идеальным газом. Выражаем из уравнения (1.1) давление: p = 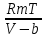 - - 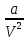 Вывод уравнения состояния Ван-дер-Ваальса в вириальном виде. (P+a/V2)(V-b)=RmT – уравнение Ван-дер-Ваальса Представим коэффициент сжимаемости газов (паров) Z в вириальном виде. Z=1+ 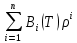 , где (1.2) , где (1.2)1 – коэффициент сжимаемости идеального газа; B1 – второй вириальный коэффициент, учитывает парное столкновение молекул газа, 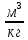 ; ;В2 = С – третий вириальный коэффициент, учитывает тройное столкновение молекул газа, 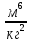 . .Ряд бесконечный, но для газов и паров сходящийся, поэтому применяется в усечённом виде (1.3). Z=1+B*ρ (1.3) Для жидкости ряд расходится и не может быть применим. Коэффициент сжимаемости газов (паров) Z показывает отношение идеальногазовой плотности 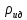 (модели Клапейрона-Менделеева) МИГ к плотности реального газа (модели Клапейрона-Менделеева) МИГ к плотности реального газа  (МРГ). (1.4) (МРГ). (1.4)Z= 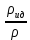 = = = =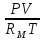 (1.4) (1.4)Представим вывод уравнения Ван-дер-Ваальса в вириальном виде и проанализируем полученный результат: Z=1+B/V+C/V2, где ρ=1/V, т.е. ограничимся тремя вириальными коэффициентами, поскольку ряд сходится. Выразим P из уравнения (1.1): p = 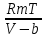 - - 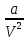 Z 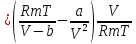 = V/(V-b)-a/VRmT = V/(V-b)-a/VRmTZ=V/(V-b)-a/VRmT Выполним математические преобразования (1.5): V/(V-b)=V*1/(V-b)=1+ 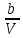 + +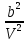 + + +….+=1+ +….+=1+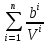 (1.5), ряд сходится (1.5), ряд сходитсяПолучаем выражение в вириальном виде (1.6): Z=1+(b-a/RmT)1/V+ b2/V2+b3/V3+…+= 1 +(b-a/RmT)1/V +  (1.6) (1.6)Из полученного выражения видно, что 1 – первый член ряда соответствует идеальному газу (МИГ), B = (b-a/RmT)1/V – второй вириальный коэффициент, С = b2/V2 – третий вириальный коэффициент. Единица представляет собой идеальногазовое состояние (абсолютную сжимаемость), последующие члены учитывают отклонение от модели идеального газа МИГ. Недостаток уравнения Ван-дер-Ваальса: силы межмолекулярного взаимодействия учитываются только во втором вириальном коэффициенте. Этот факт сразу обнаруживает ограниченность этой модели: силам межмолекулярного взаимодействия априори ставиться второстепенная роль по сравнению с собственным объёмом молекул газа (пара). При больших удельных объёмах и сравнительно невысоких давлениях уравнение Ван-дер-Ваальса практически вырождается в уравнение идеального газа Клапейрона-Менделеева Уравнение Ван-дер-Ваальса с качественной стороны достаточно хорошо описывает свойства неидеальных газов, но результаты численных расчетов не всегда согласуются с экспериментальными данными. В ряде случаев это объясняется склонностью молекул неидеального газа к ассоциации в комплексы, наглядным примером может служить молекулы водяного пара. Пример домашнего задания №1 В баллоне содержится газ известных значений температуры 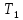 и давления и давления 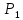 . Термическое уравнение, характеризующее состояние газа, является моделью вириального уравнения неидеального газа Боголюбова-Майера в усеченном виде. . Термическое уравнение, характеризующее состояние газа, является моделью вириального уравнения неидеального газа Боголюбова-Майера в усеченном виде.В задании варьируются параметры изучаемого объекта (газа). Размеры баллона: Диаметр 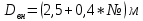 Высота 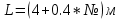 Параметры рабочего тела (газа), содержащегося в газгольдере: 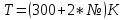 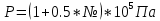 , где № – номер варианта , где № – номер вариантаХарактеристики рабочего тела (газа):
Определить: 1) массу газа, содержащегося в баллоне (m, кг). Для определения плотности газа использовать уравнение Ван-дер-Ваальса, представленное в вириальном виде. Объем баллона считать по уравнению следующему соотношению (1.1): V = 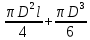 , (1) , (1), где V - объем баллона, [ 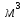 ]; ];D – диаметр цилиндрической части баллона, [ 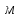 ]; ];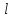 – длина цилиндрической части баллона, [м]; – длина цилиндрической части баллона, [м];Толщиной стенок пренебречь. 2) Определить значения давления газа в баллоне 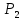 , если все содержимое баллона нагревают до температуры , если все содержимое баллона нагревают до температуры 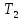 = = 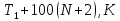 . Процесс считать равновесным. . Процесс считать равновесным.Теплопроводность стенок баллона пренебречь. Объем баллона жёсткий. 3) Рассчитать величину подведённой теплоты к газу. 4) Представить (PV), (TS) диаграммы процесса. Критические параметры и теплофизические характеристики газов представлены в таблице (1) и таблице (2). 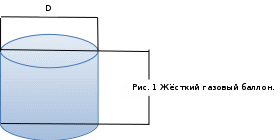 Таблица 1. Критические параметры
Таблица 2. Теплофизические характеристики газов. Константы теплоемкости газов: 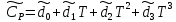 , , 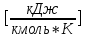 ; ;Константы уравнения Антуана: A, B, C; Теплота парообразования при нормальном барометрической температуре 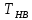 , [K] : , [K] : 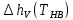 , [ , [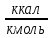 ]; ];
Пример домашнего задания №2 В задании варьируются параметры изучаемого объекта (газа). В цилиндрическом газгольдере постоянного давления содержится газ: 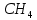 (четные варианты) (четные варианты)  (нечетные варианты) (нечетные варианты)Размеры газгольдера: Диаметр колокола 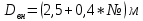 Высота расположения колокола 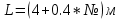 Параметры рабочего тела (газа), содержащегося в газгольдере: 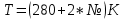 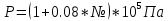 , где № – номер варианта , где № – номер вариантаХарактеристики рабочего тела (газа):
Определить: m, массу газа; кг. Термическое уравнение состояния газа: а) Уравнение Ван-дер-Ваальса, представленное в вириальном виде; б) Термическое уравнение состояния неидеального газа Боголюбова-Майера в усеченном виде (вириальная форма). Сделать вывод о полученных результатах, сравнить их. В дальнейших расчетах использовать только уравнение Боголюбова-Майера в усеченной форме. Т2, К – температуру газа в газгольдере, если положение колокола повышается на Δl12 = 75+0,5N см; L2 = L1+ Δl12 . В конечном состоянии (Т2;Р) газ считать идеальным газом Клапейрона-Менделеева. Количество теплоты Q12р, поглощенной газом при повышении температуры Т1-Т2. Q12р = m 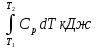 , где Ср=f(T) , где Ср=f(T)Cp = 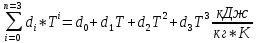 Работу деформации всей массы газа, при повышении Т; кДж Wv12p=p 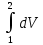 (Па*м3=Дж) (Па*м3=Дж)Представить pv ts диаграммы процесса. Газго́льдер (англ. gas-holder) — резервуар для хранения газообразных веществ, таких, например, как природный газ, биогаз, сжиженный нефтяной газ, воздух и т. д. Существуют газгольдеры переменного и постоянного объёма. Газгольдеры переменного объёма хранят газ при температуре окружающей среды и давлении, близком к атмосферному. Объём контейнера изменяется с изменением количества хранимого газа, для больших газгольдеров он может достигать 50 000 м³ при диаметре цилиндрического хранилища 60 м. Газгольдеры могут изготавливаться из железобетона, стали, резины или прорезиненной материи. Газгольдеры постоянного объёма представляют собой цилиндрические или сферические стальные резервуары и способны хранить газ при давлении до 1,8 МПа (≈ 18 атм). 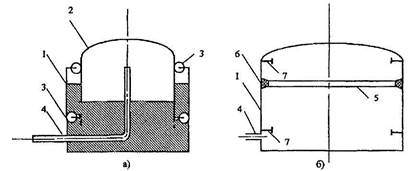 Принципиальная схема газгольдеров низкого давления: а) мокрый; б) сухой;1 - резервуар; 2 - колокол; 3 - ролики; 4 - газопровод; 5 - шайба; 6 - уплотнение; 7 - ограничитель хода. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


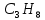
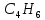
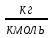
 , K
, K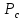 , атм
, атм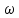

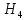
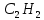
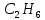

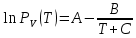 , мм рт. ст.
, мм рт. ст.