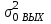АНАЛИЗ ХАРАКТЕРИСТИК ЦИФРОВЫХ ФИЛЬТРОВ ДЛЯ ОБРАБОТКИ ОДНОМЕРНЫХ СИГНАЛОВ по дисциплине «Программирование логических интегральны. лабор_1. Анализ характеристик цифровых фильтров для обработки одномерных сигналов по дисциплине Программирование логических интегральных схем
 Скачать 2.75 Mb. Скачать 2.75 Mb.
|
|
Лабораторная работа №1 АНАЛИЗ ХАРАКТЕРИСТИК ЦИФРОВЫХ ФИЛЬТРОВ ДЛЯ ОБРАБОТКИ ОДНОМЕРНЫХ СИГНАЛОВ по дисциплине «Программирование логических интегральных схем» 1. Цель работы: Изучение основ анализа характеристик цифровых фильтров. Введение Целью настоящей работы является изучение основ анализа характеристик цифровых фильтров. Линейный цифровой фильтр (ЦФ) это устройство, в котором текущий отсчёт выходного сигнала представлен в виде линейной комбинации текущего отсчёта входного сигнала и предыдущих входных и выходных отсчётов. Обработка входных данных линейным ЦФ (без учёта эффектов квантования данных) описывается разностным уравнением 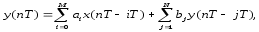 где x(nT) и y(nT) - отсчёты входного и выходного сигналов фильтра соответственно; 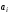 и и 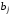 - коэффициенты фильтра; M и N - целые числа, определяющие порядок фильтра; T- период дискретизации входных данных. - коэффициенты фильтра; M и N - целые числа, определяющие порядок фильтра; T- период дискретизации входных данных.К основным характеристикам линейных ЦФ относятся: передаточная (системная) функция в Z - форме; импульсная и переходная характеристики; амплитудно-частотная и фазочастотная характеристики; точностные характеристики. Передаточной функцией H(z) фильтра называют отношение Z - образа выходного сигнала Y(z) к Z - образу входного сигнала фильтра X(z) при нулевых начальных условиях, т.е. при y(-T) = y(-2T) = ... = y(-NT) = 0 и, кроме того, x(nT) = 0 при n < 0: 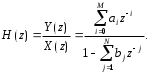 Исследование параметров цифровых фильтров На основе приведенных ниже передаточных функций (таб. 1.1) определим коэффициенты цифровых фильтров и, подставляя их в программные модули, получим ИХ, ПХ, АЧХ и ФЧХ. Структурные схемы исследуемых цифровых звеньев. Таблица 1.1 – Передаточные функции исследуемых цифровых фильтров
1) Цифровой интегратор с ограниченным временем суммирования (М=4) 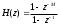 Коэффициенты фильтра: По полученным коэффициентам построим структурную схему фильтра (рис. 1.1). 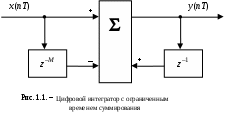 Импульсная характеристика интегратора с ограниченным временем суммирования представлена на рис.1.2. 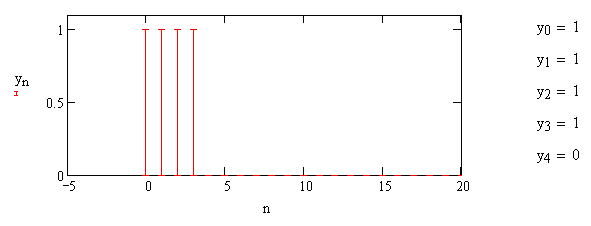 Рис. 1.2 – Импульсная характеристика интегратора с ограниченным временем суммирования Переходная характеристика интегратора с ограниченным временем суммирования представлена на рис.1.3. 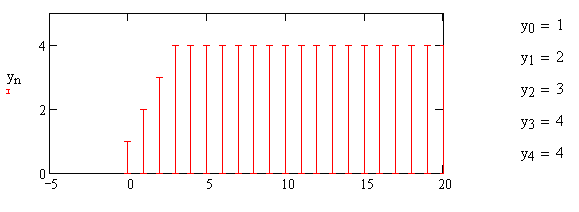 Рис. 1.3 – Переходная характеристика интегратора с ограниченным временем суммирования АЧХ интегратора с ограниченным временем суммирования представлена на рис.1.4. 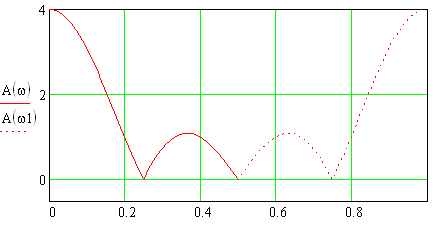 Рис. 1.4 – АЧХ интегратора с ограниченным временем суммирования ФЧХ интегратора с ограниченным временем суммирования представлена на рис.1.5. 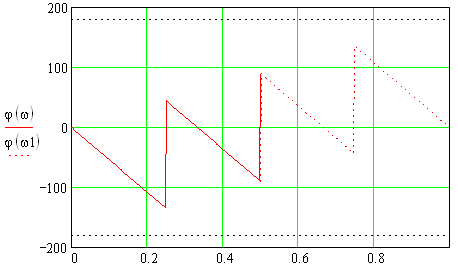 Рис. 1.5 – ФЧХ интегратора с ограниченным временем суммирования 2) Цифровой дифференциатор (В1Р) 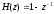 Коэффициенты фильтра: 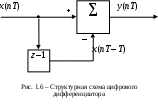 По полученным коэффициентам построим структурную схему фильтра (рис. 1.6). Импульсная характеристика цифрового дифференциатора (В1Р) представлена на рис.1.7. 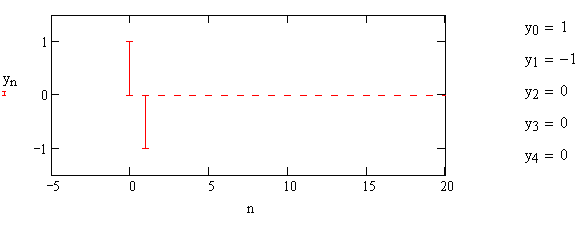 Рис. 1.7 – Импульсная характеристика цифрового дифференциатора (В1Р) Переходная характеристика цифрового дифференциатора (В1Р) представлена на рис.1.8. 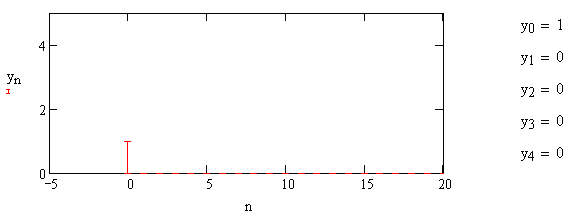 Рис. 1.8 – Переходная характеристика цифрового дифференциатора (В1Р) АЧХ цифрового дифференциатора (В1Р) представлена на рис.1.9. 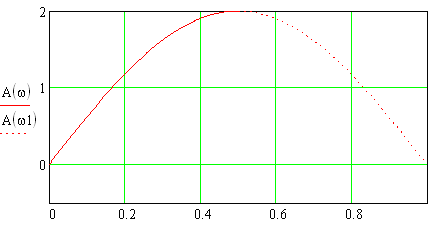 Рис. 1.9 – АЧХ цифрового дифференциатора (В1Р) ФЧХ цифрового дифференциатора (В1Р) представлена на рис.1.10. 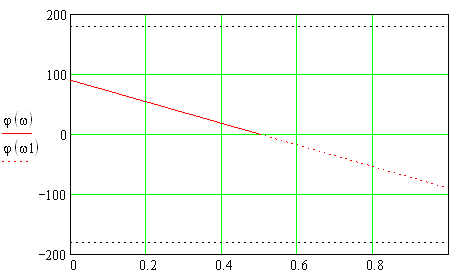 Рис. 1.10 – ФЧХ цифрового дифференциатора (В1Р) 3) Вычислитель второй разности (В2Р) 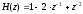 Коэффициенты фильтра: 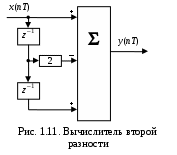 По полученным коэффициентам построим структурную схему фильтра (рис. 1.11). Импульсная характеристика вычислителя второй разности (В2Р) представлена на рис.1.12. 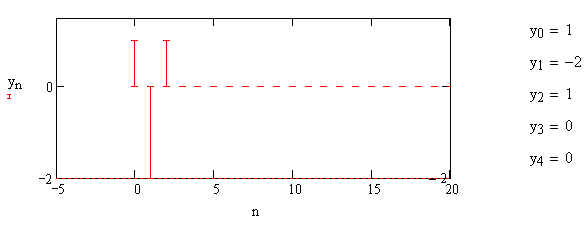 Рис. 1.12 – Импульсная характеристика вычислителя второй разности (В2Р) Переходная характеристика вычислителя второй разности (В2Р) представлена на рис.1.13. 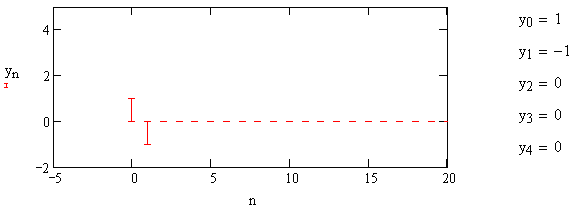 Рис. 1.13 – Переходная характеристика вычислителя второй разности (В2Р) АЧХ вычислителя второй разности (В2Р) представлена на рис.1.14. 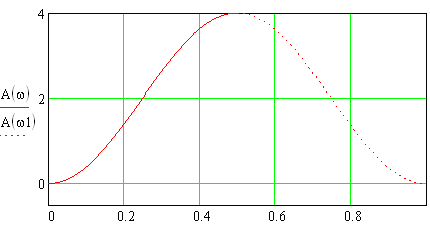 Рис. 1.14 – АЧХ вычислителя второй разности (В2Р) ФЧХ вычислителя второй разности (В2Р) представлена на рис.1.15. 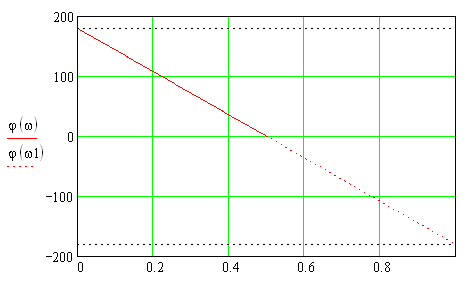 Рис. 1.15 – ФЧХ вычислителя второй разности (В2Р) 4) Всепропускающее звено (K=0.3) 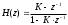 Коэффициенты фильтра: АЧХ всепропускающего звена представлена на рис.1.16. 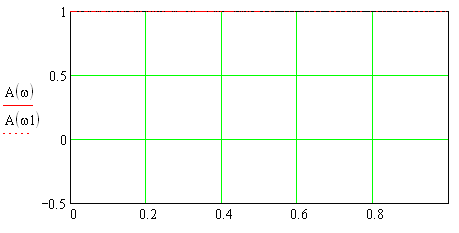 Рис. 1.16 – АЧХ всепропускающего звена Импульсная характеристика всепропускающего звена представлена на рис.1.17. 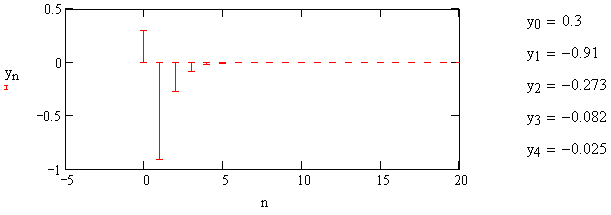 Рис. 1.17 – Импульсная характеристика всепропускающего звена Переходная характеристика всепропускающего звена представлена на рис.1.18. 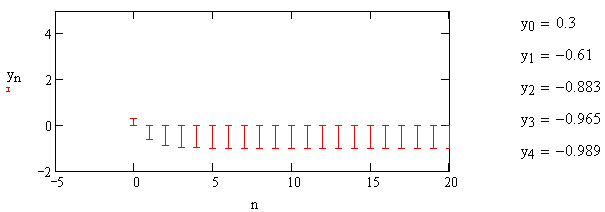 Рис. 1.18 – Переходная характеристика всепропускающего звена ФЧХ всепропускающего звена представлена на рис.1.19. 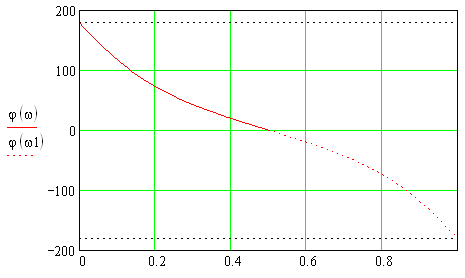 Рис. 1.19 – ФЧХ всепропускающего звена По полученным коэффициентам построим структурную схему фильтра (рис. 1.20). 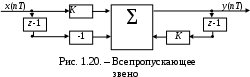 5) Сглаживающее звено (К=0,5) 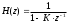 Коэффициенты фильтра: АЧХ сглаживающего звена представлена на рис.1.21. 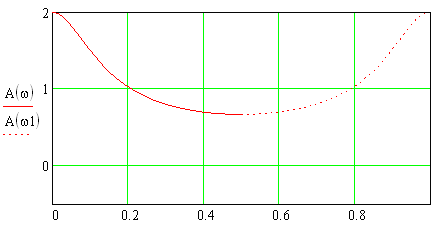 Рис. 1.21 – АЧХ сглаживающего звена Импульсная характеристика сглаживающего звена представлена на рис.1.22. 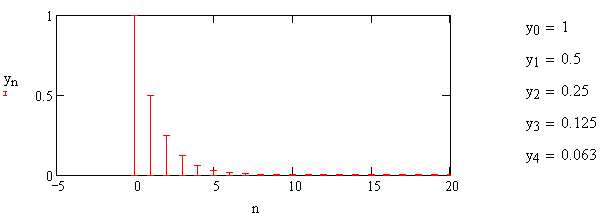 Рис. 1.22 – Импульсная характеристика сглаживающего звена Переходная характеристика сглаживающего звена представлена на рис.1.23. 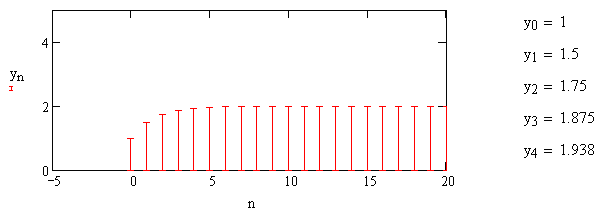 Рис. 1.23 – Переходная характеристика сглаживающего звена ФЧХ сглаживающего звена представлена на рис.1.24. 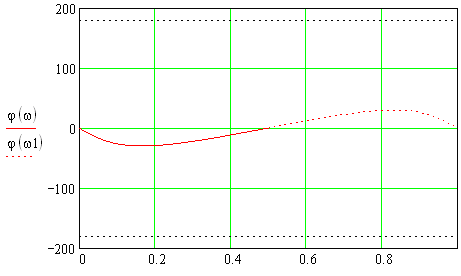 Рис. 1.24 – ФЧХ сглаживающего звена По полученным коэффициентам построим структурную схему фильтра (рис. 1.25). 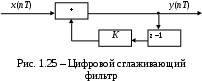 2. На основе варианта №5 получить АЧХ, ФЧХ, ИХ и ПХ. Опишите особенности характеристик исследованного фильтра. Изменяя один из коэффициентов в рекурсивной или нерекурсивной частях ЦФ опишите изменения, произошедшие с характеристиками фильтра. Объясните эти изменения. Приведите структурную схему фильтра.  Режекторный фильтр— фильтр с двумя полосами пропускания (от 0 до ωсн и от ωсв до ∞) и одной полосой подавления. Системная функция режекторного фильтра: 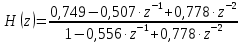 АЧХ и ФЧХ фильтра: Используя программный модуль h(jw) получим следующие АЧХ и ФЧХ фильтра: 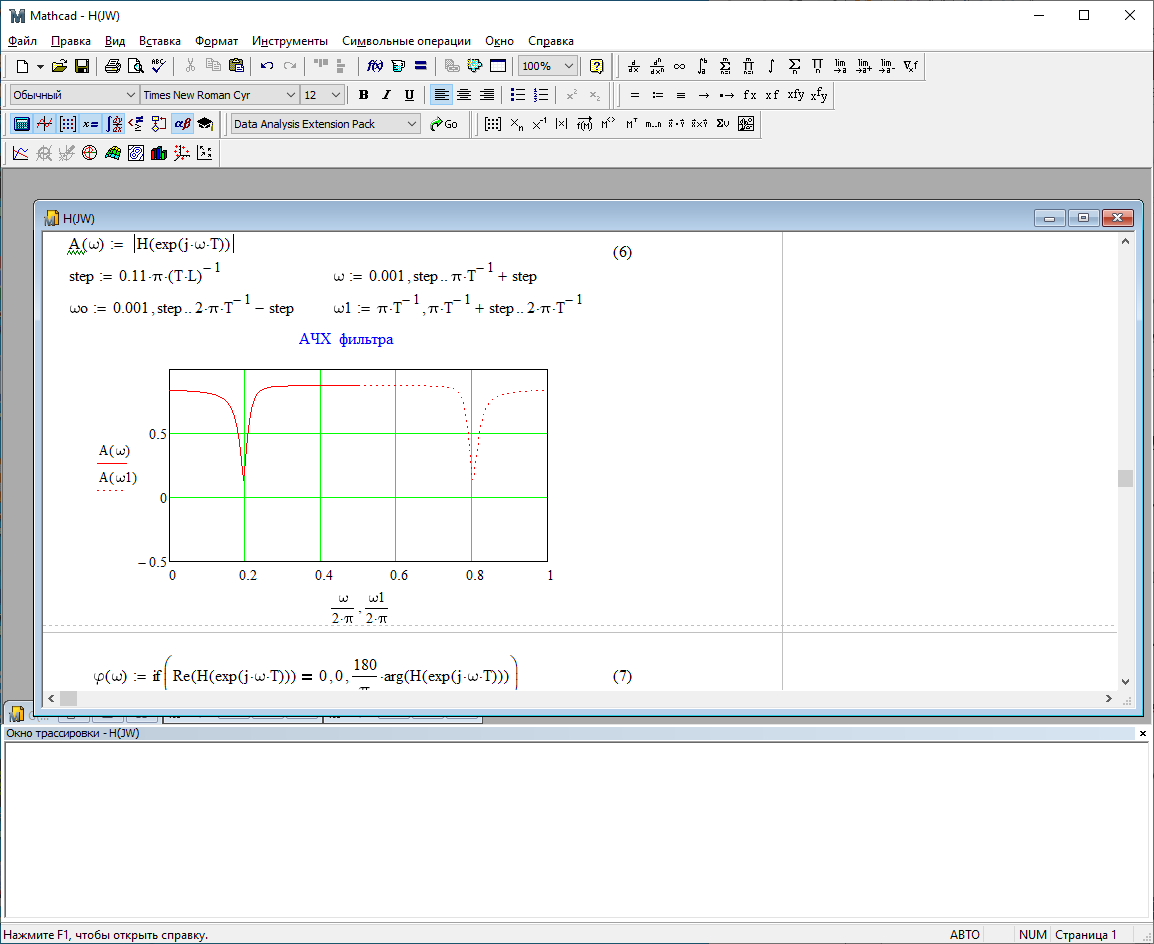 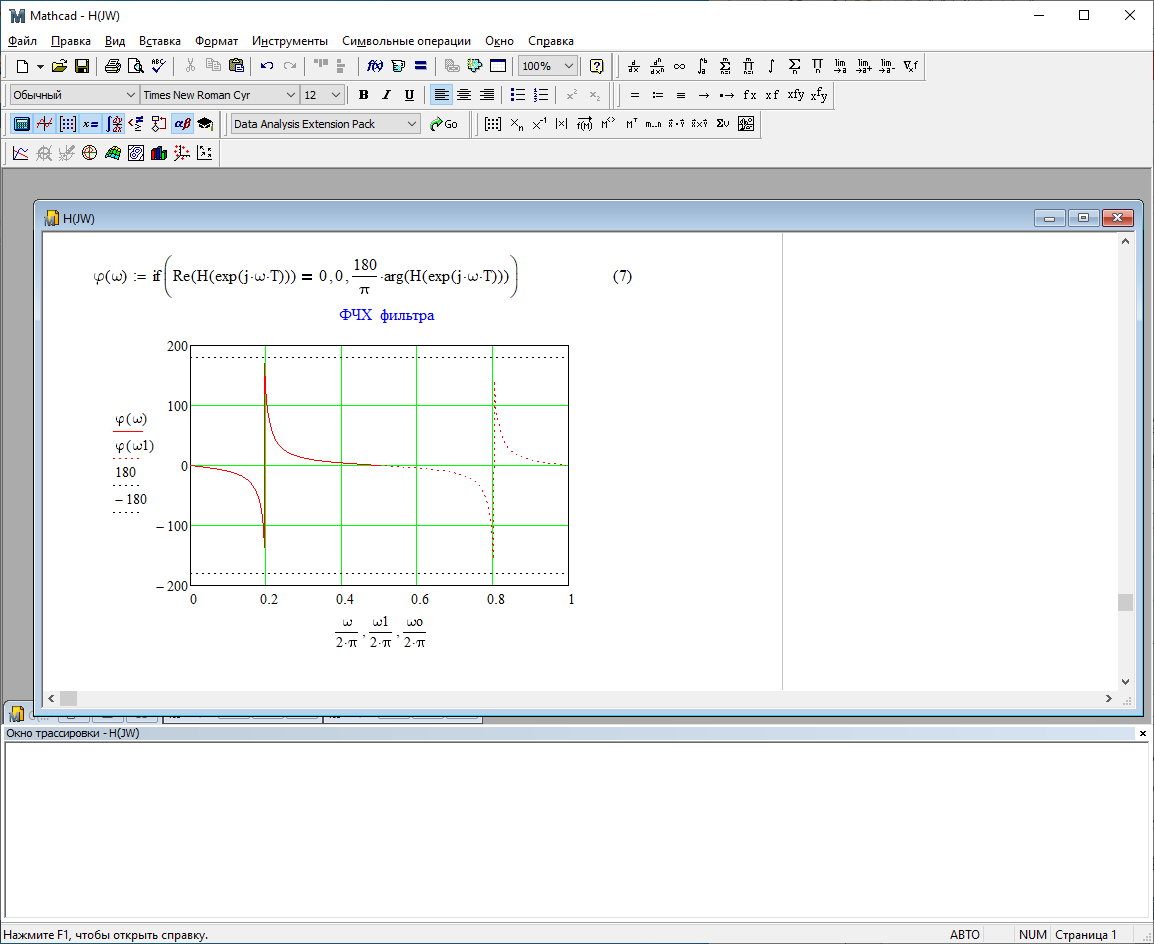 Рис.2.1 – АЧХ фильтра. Рис.2.2 – ФЧХ фильтра. Используя программный модуль h(nT) получим импульсную характеристику: 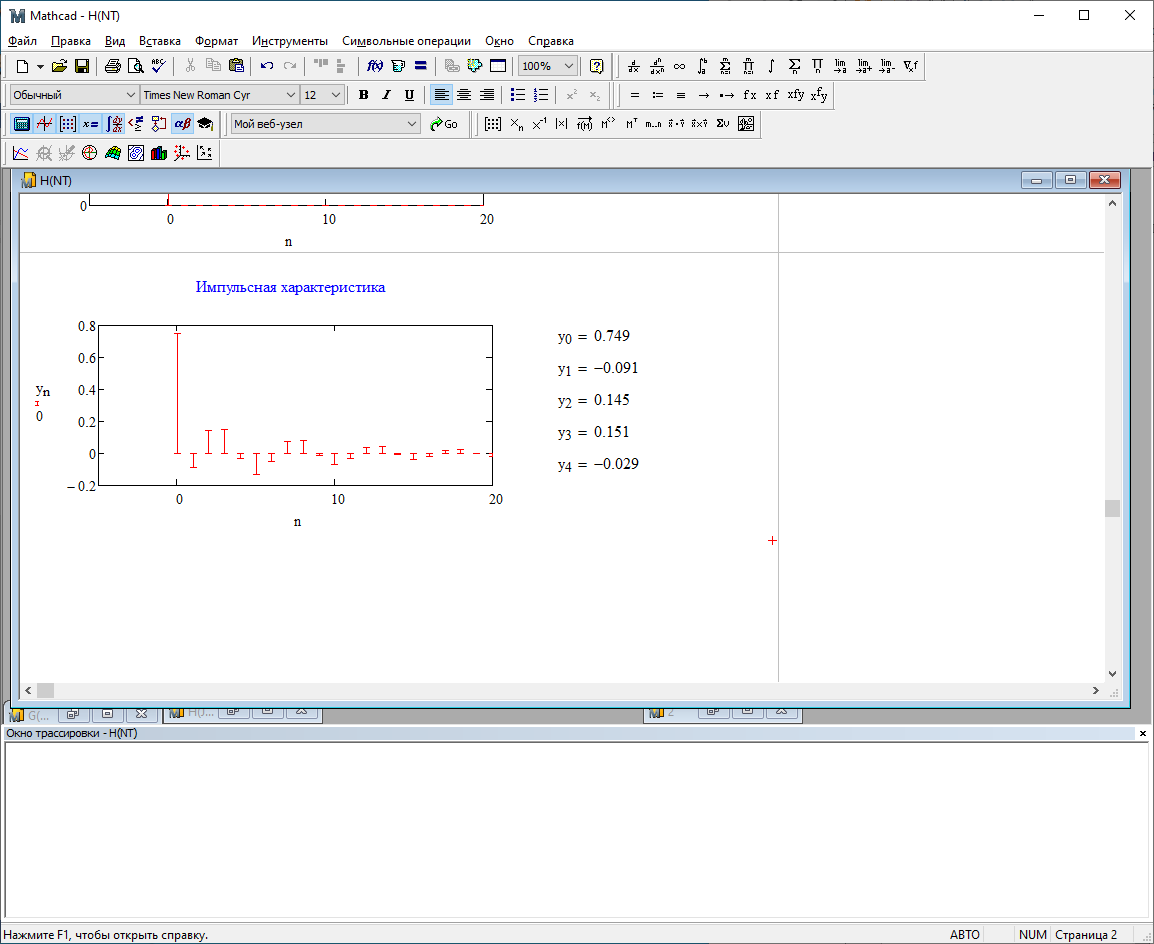 Рис.2.3 – Импульсная характеристика. Переходная характеристика: Используя программный модуль g(nT) получим переходную характеристику: 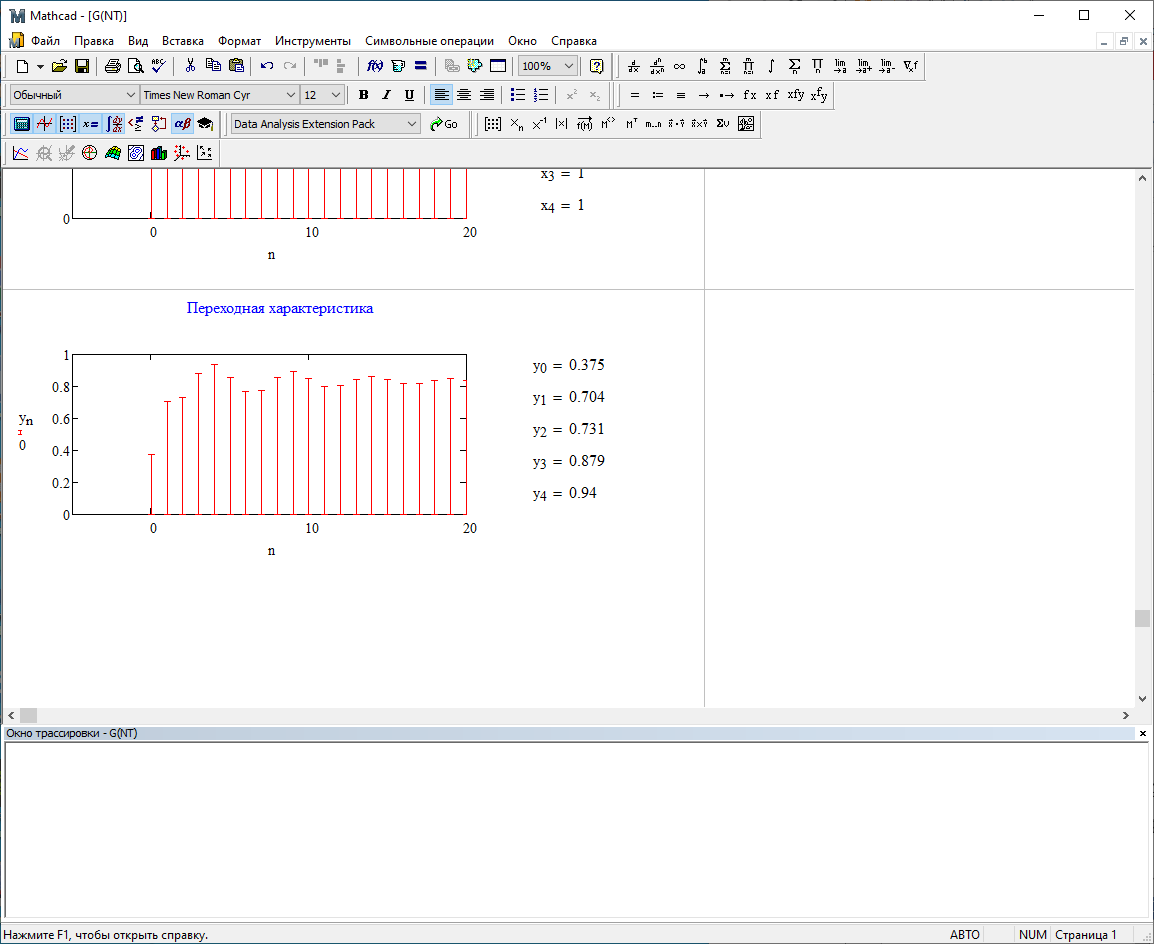 Рис.2.4 – Переходная характеристика. 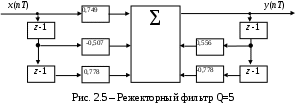 Структурная схема режекторного фильтра приведена на рис.2.5: Изменим коэффициент b1 = 0.177. Рассмотрим произошедшие изменения. Импульсная характеристика: 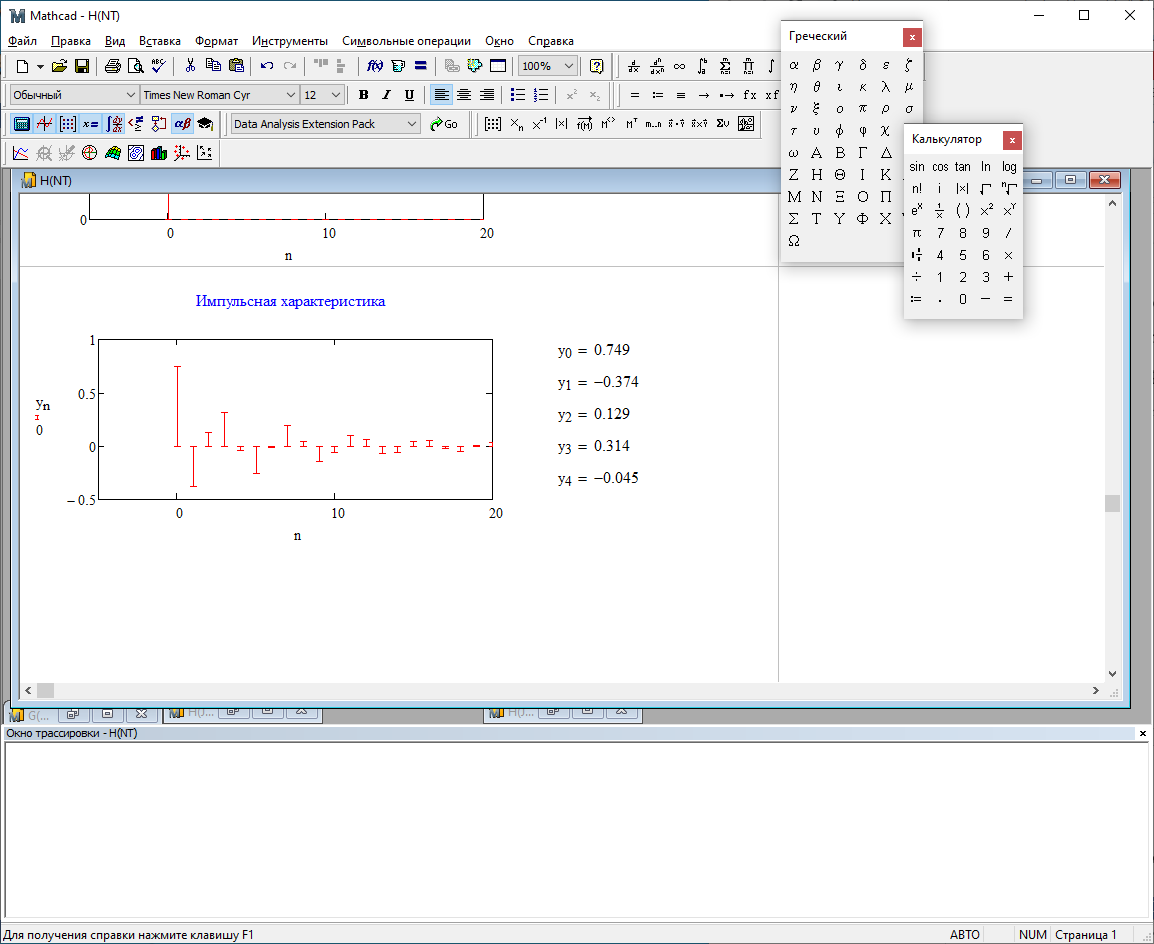 Рис.2.6 – Импульсная характеристика. Переходная характеристика: 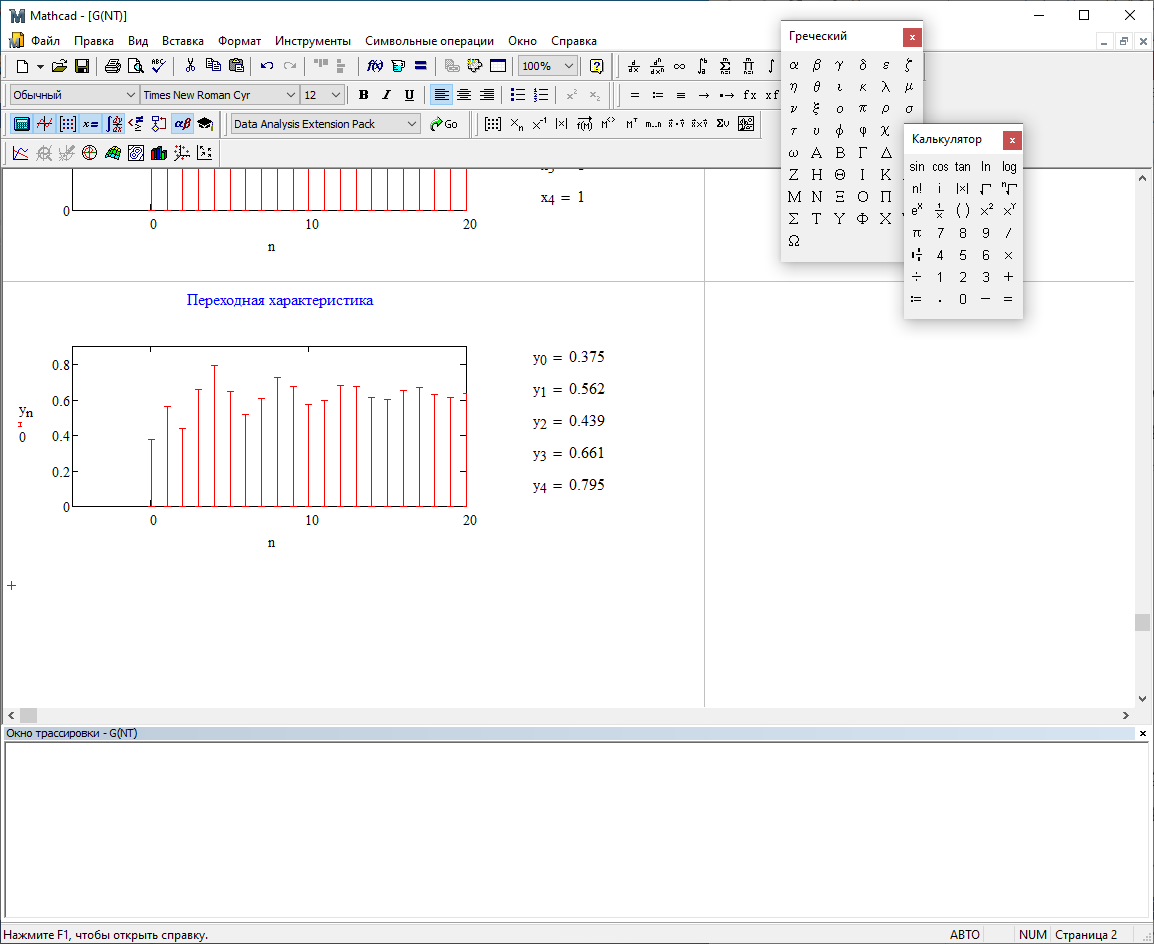 Рис.2.7 – Переходная характеристика. АЧХ и ФЧХ фильтра: 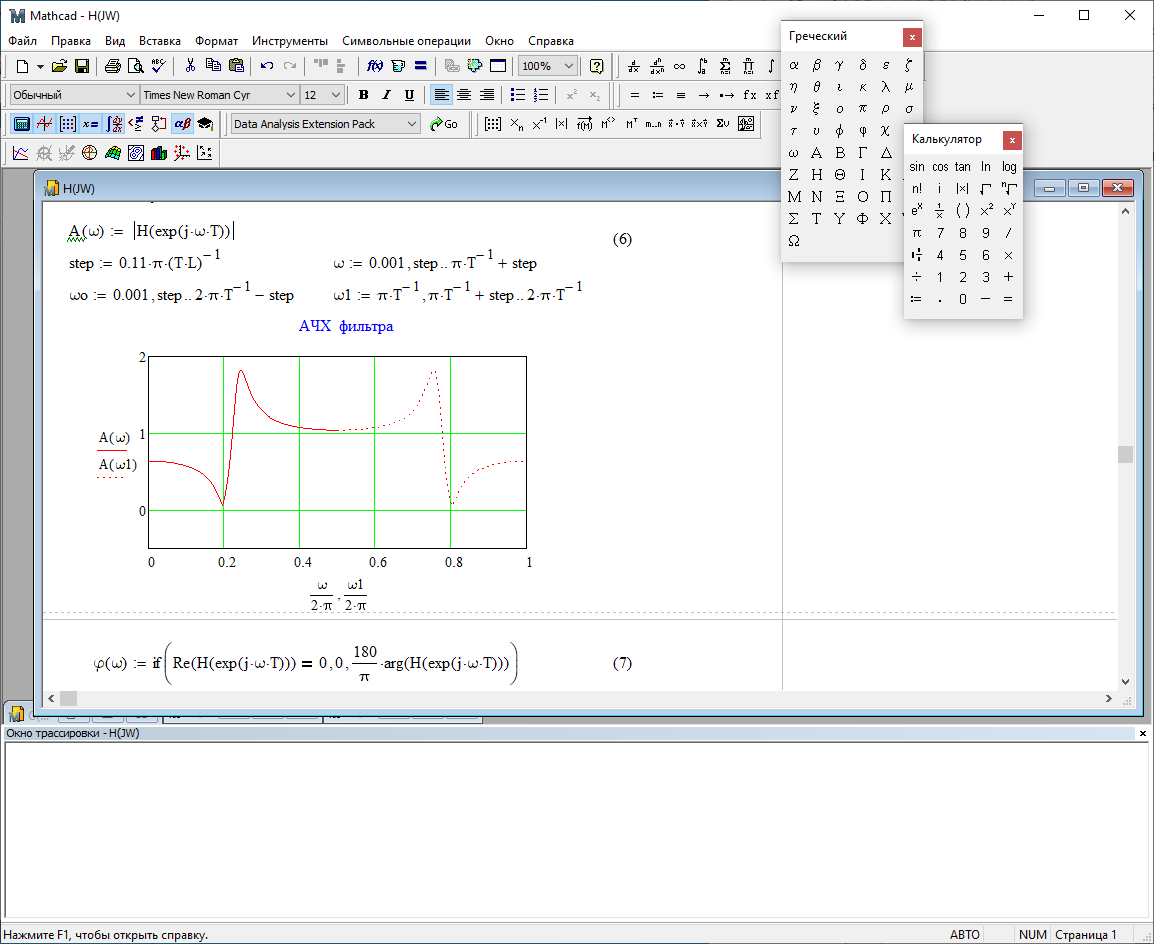 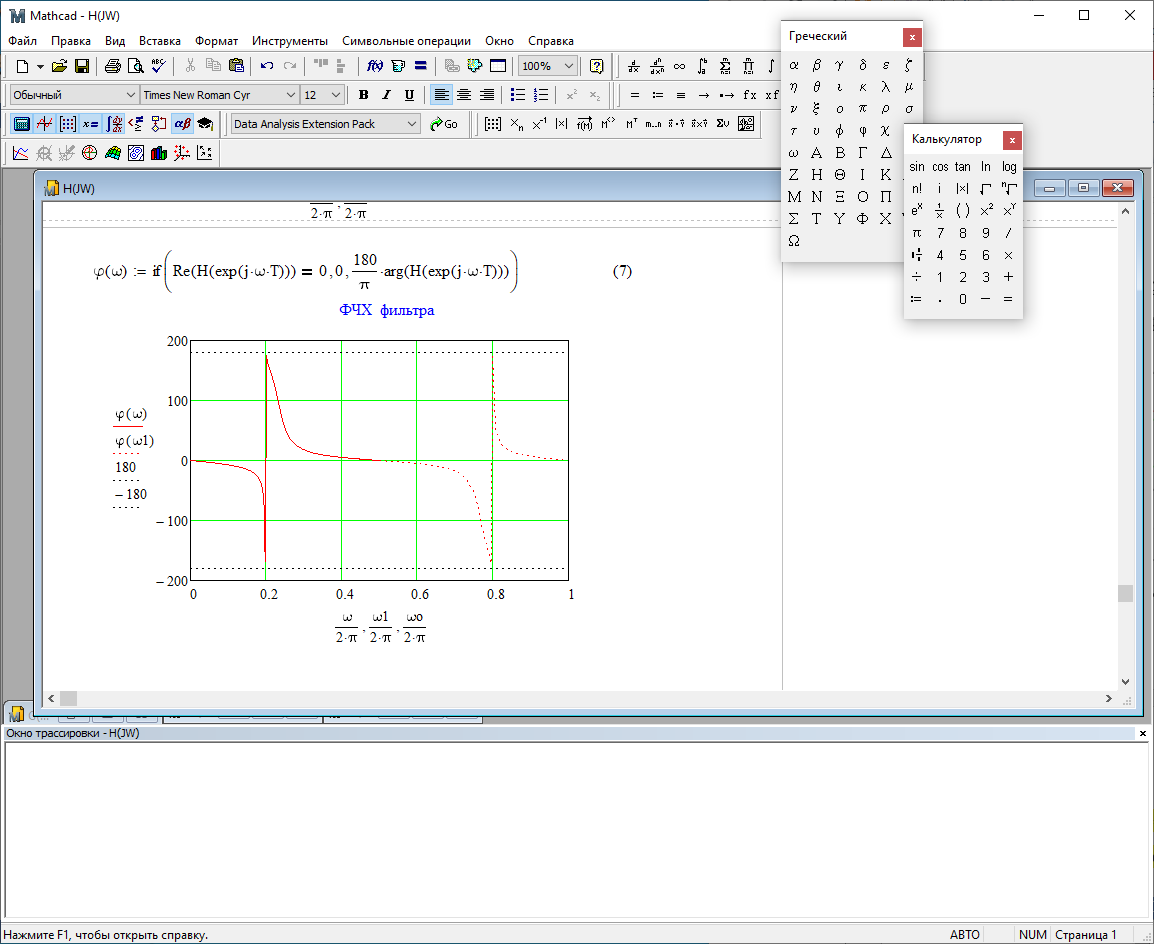 Рис.2.8 – АЧХ фильтра. Рис.2.9 – ФЧХ фильтра. При уменьшении b1 до 0,177 в ИХ и ПХ значительных изменений не наблюдается. изменился только первый отсчет. Стал выше, вследствие того, что мы увеличили а0. АЧХ фильтра стала приближенной к АЧХ полосового фильтра поднялась с 1 до 1.2 на нижних и верхних частотах. ФЧХ фильтра изменилась незначительно. В области средних частот характеристика сильно исказилась. Появился «прогиб» характеристики вверх и вниз. 3. Дискретная свертка сигналов и входного сигнала с импульсной характеристикой ЦФ. Зададим два входных сигнала: 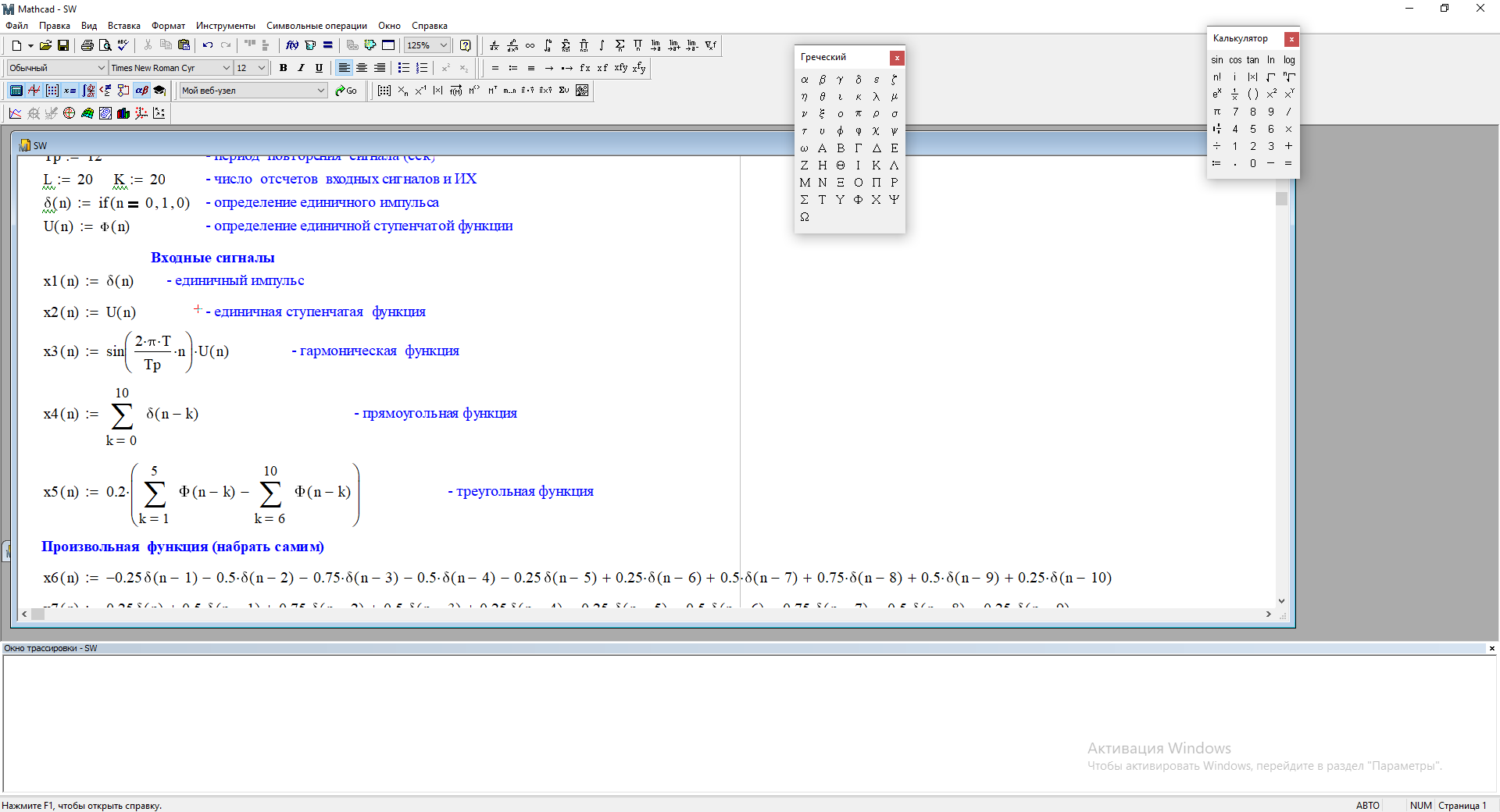   Используя программный модуль sw получим следующую свертку этих сигналов: 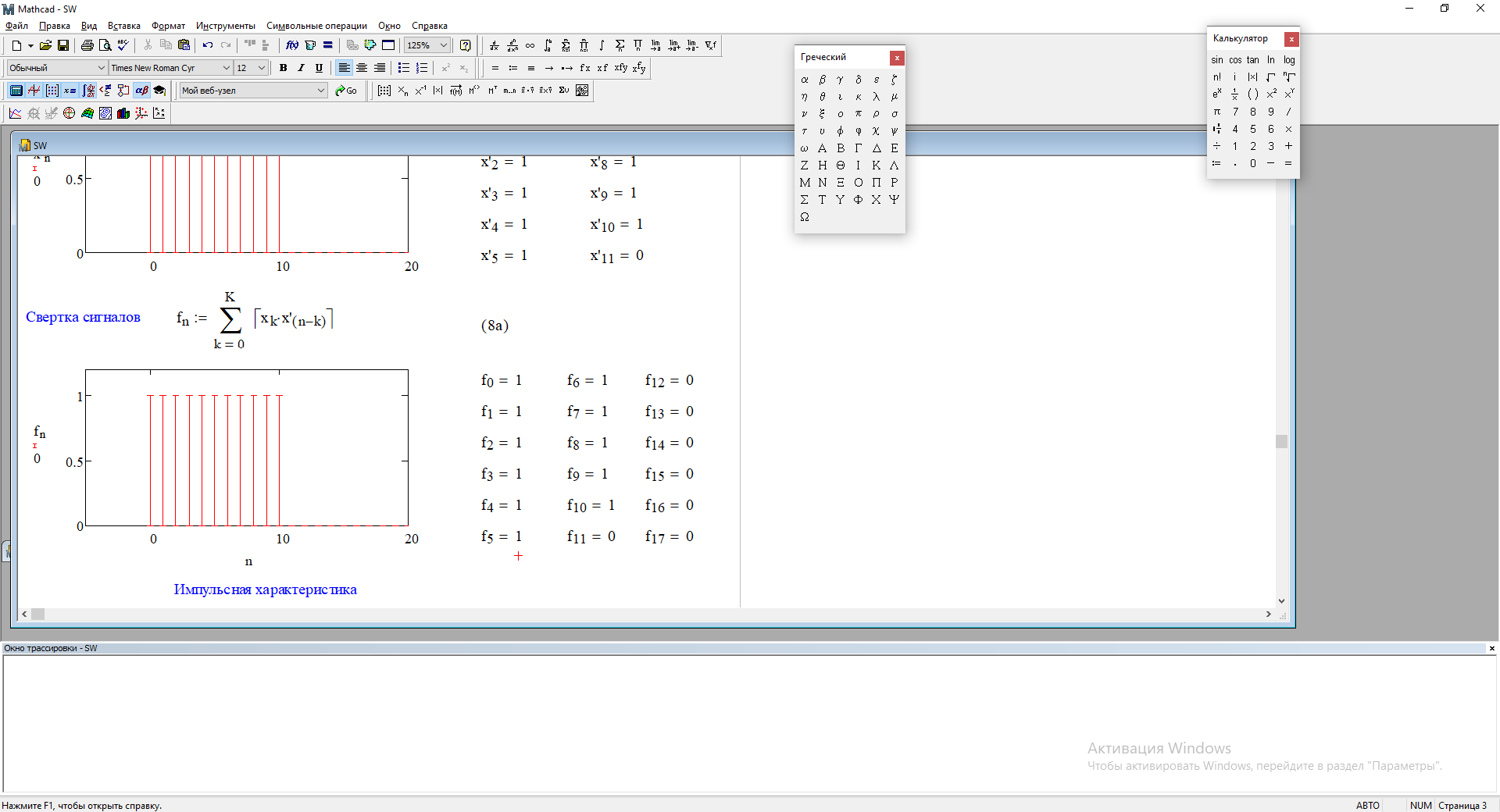 Рис. 3.1 – Свертка двух сигналов. Возьмем, из предложенных в задании, импульсную характеристику: 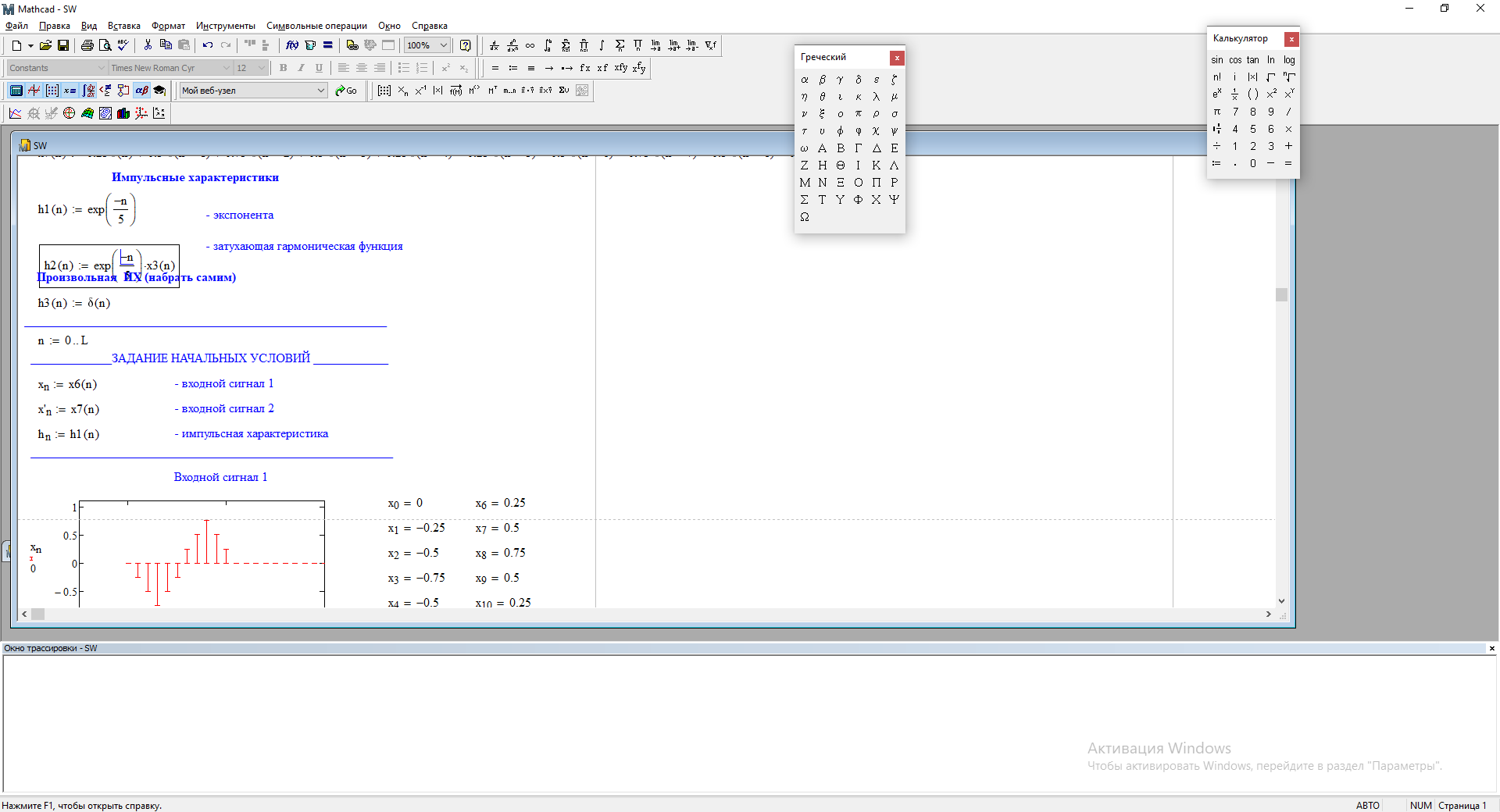  Получим выходной сигнал (свертку с импульсной характеристикой): 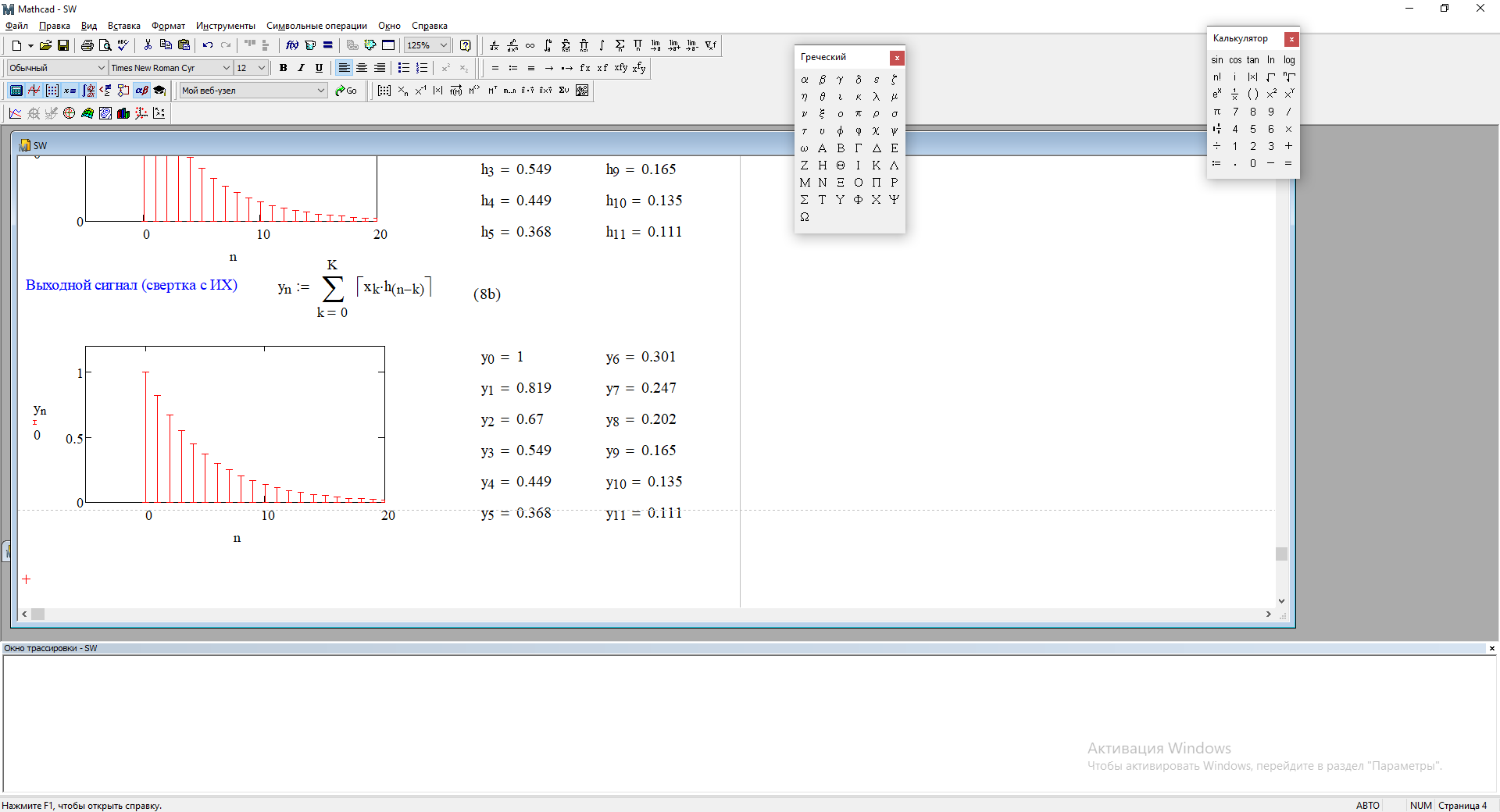 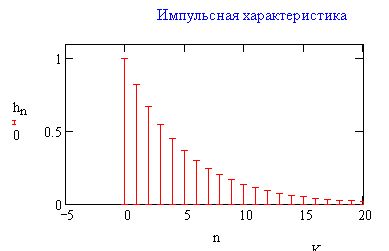 Рис.3.2 – Импульсная характеристика. Рис.3.3 – Свертка с импульсной характеристикой. 4. Дискретная свертка сигналов и входного сигнала с импульсной характеристикой ЦФ (сигналы взяты в соответствии с вариантом №5).  Аналитическое описание x6(n) через единичные импульсы будет иметь вид: 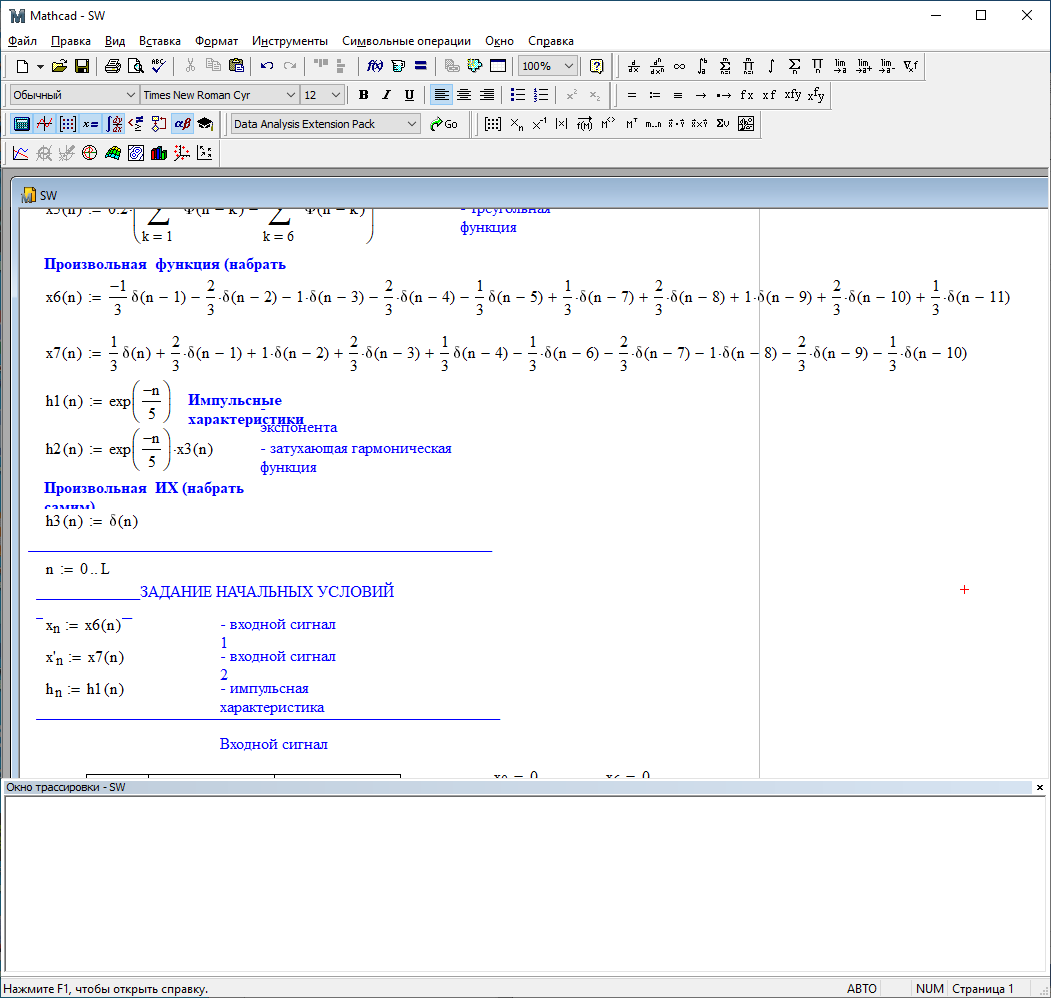 Симметричный ему сигнал x7(n) будет иметь вид:  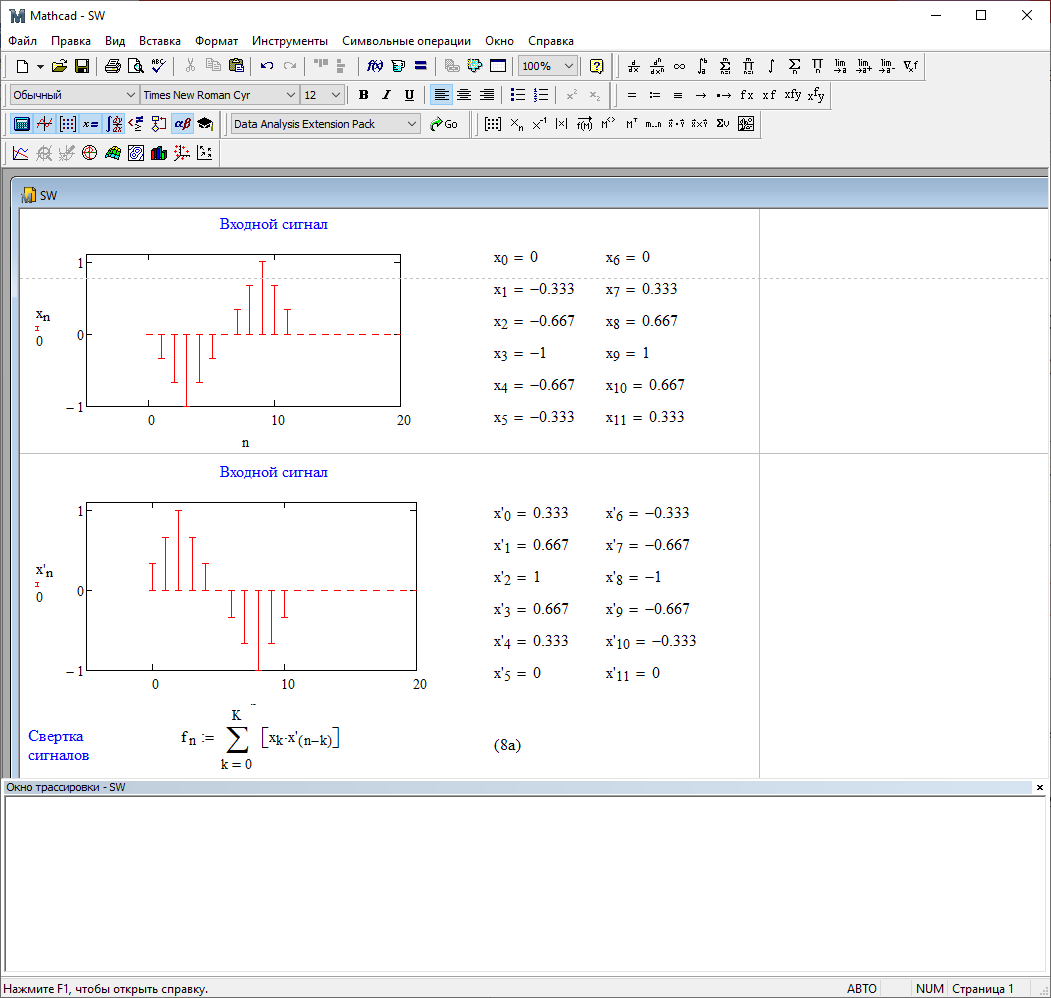 Рис. 4.1 – Сигнал x6(n)  Рис. 4.2 – Сигнал x7(n) Дискретная свёртка данного сигнала с симметричным сигналом x7(n): 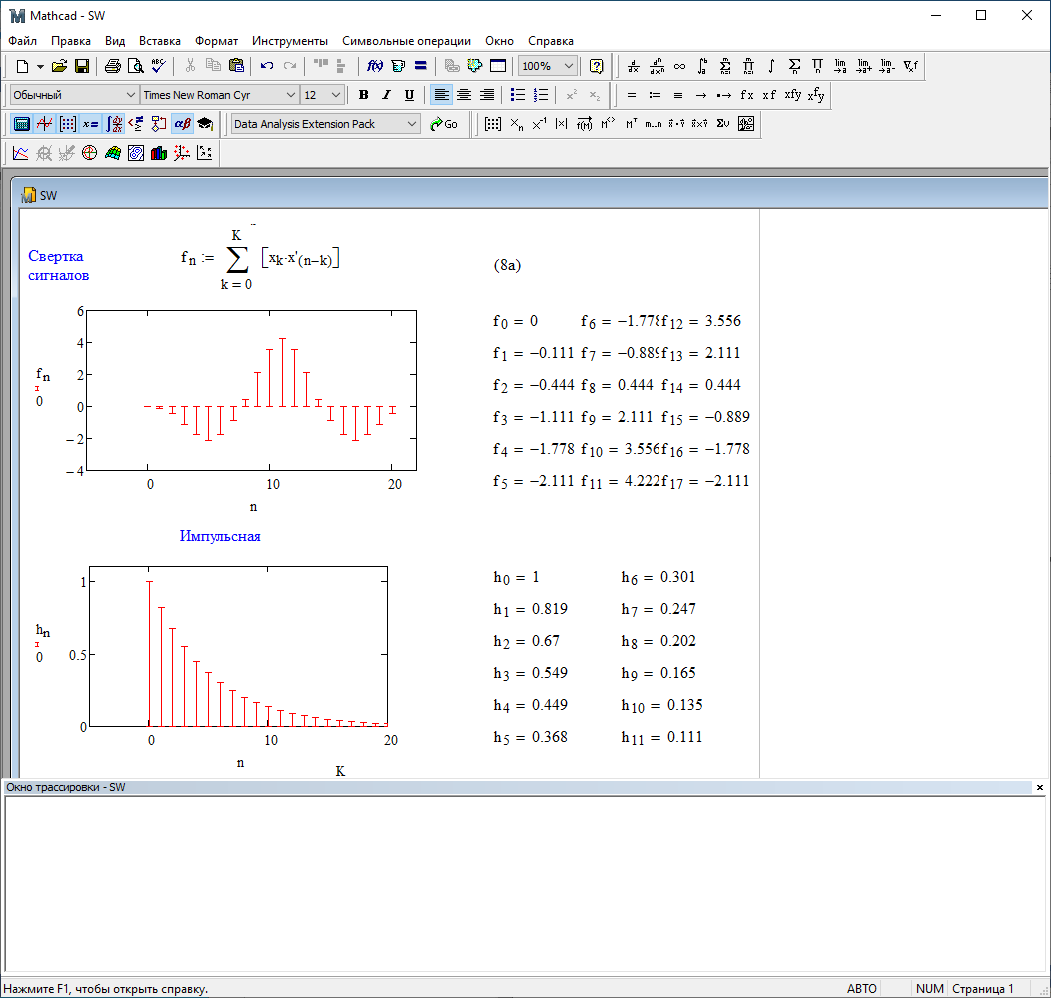 Рис. 4.3 – Свертка двух сигналов. Возьмем, из предложенных в задании, импульсную характеристику   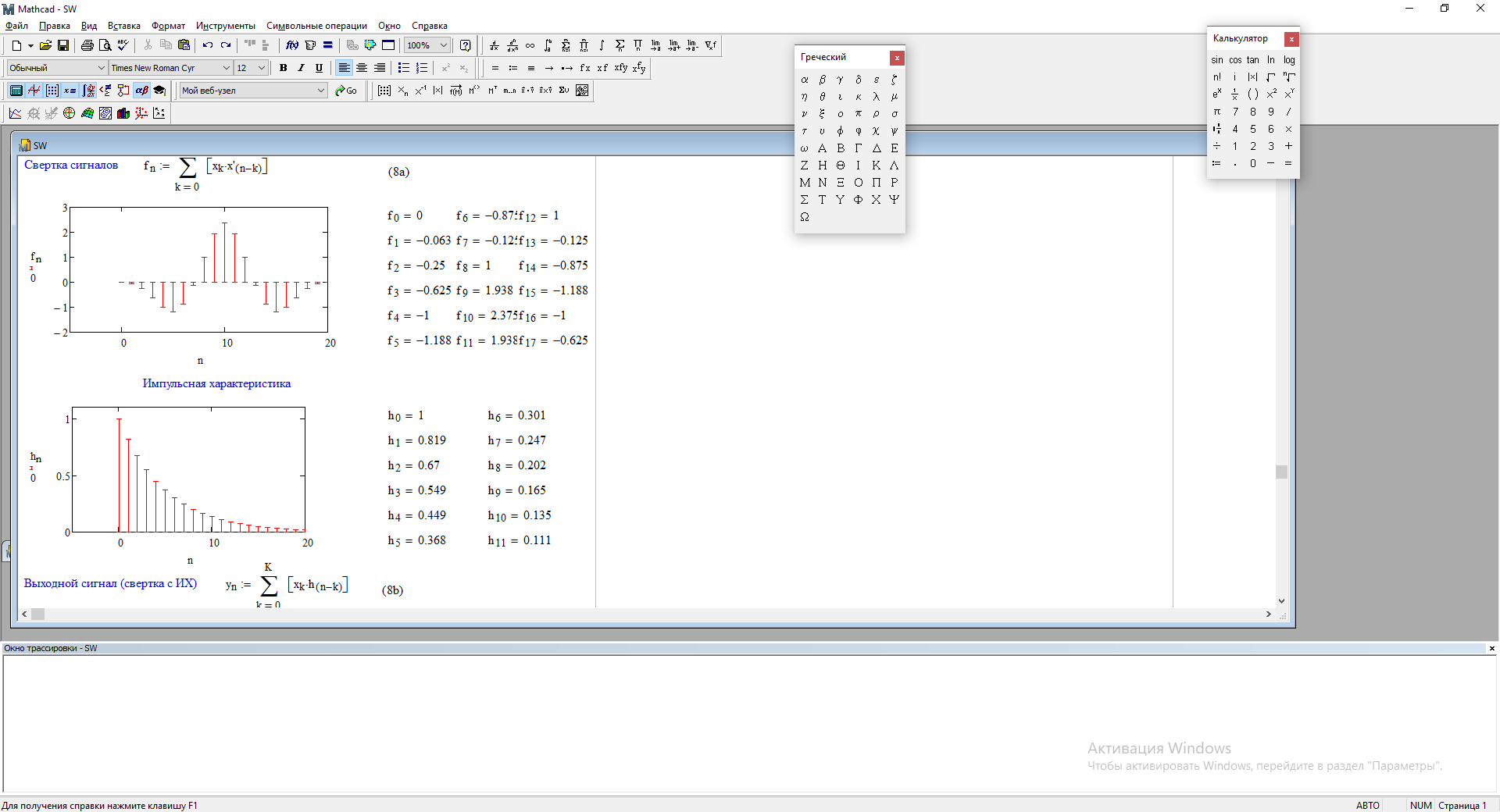 Рис. 4.4 – Импульсная характеристика Дискретная свёртка данного сигнала с импульсной характеристикой 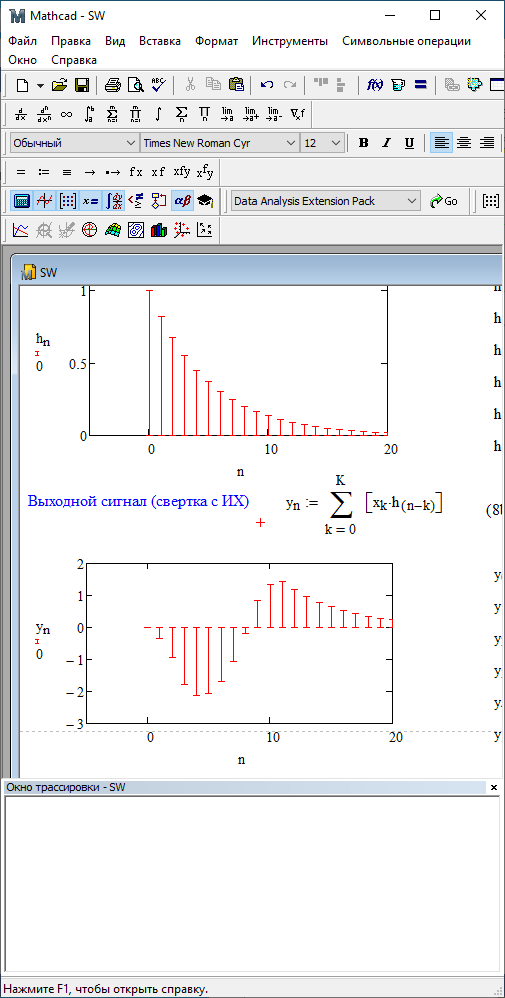 Рис. 4.5 – Дискретная свертка с ИХ. Возьмем другую импульсную характеристику: 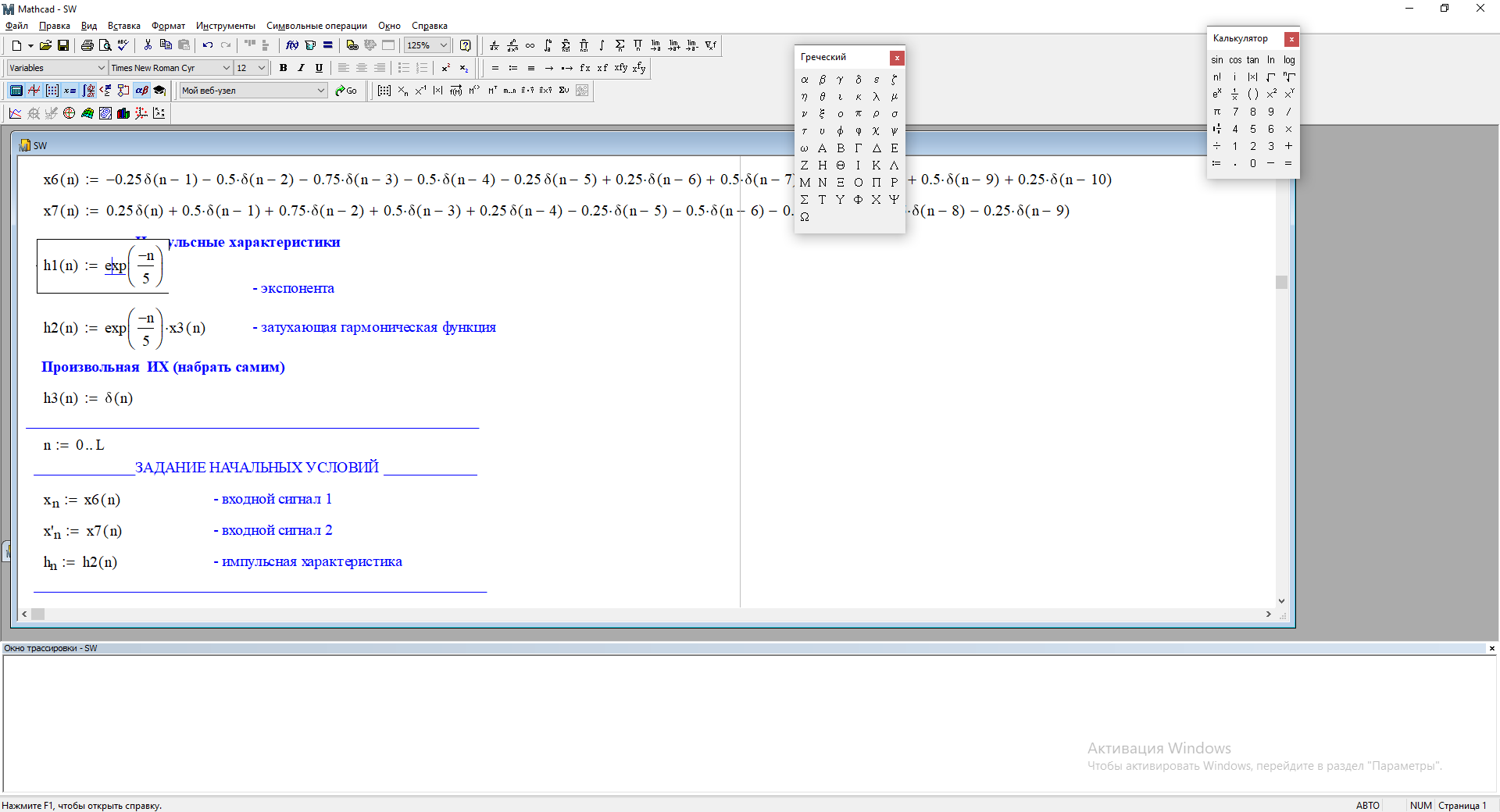 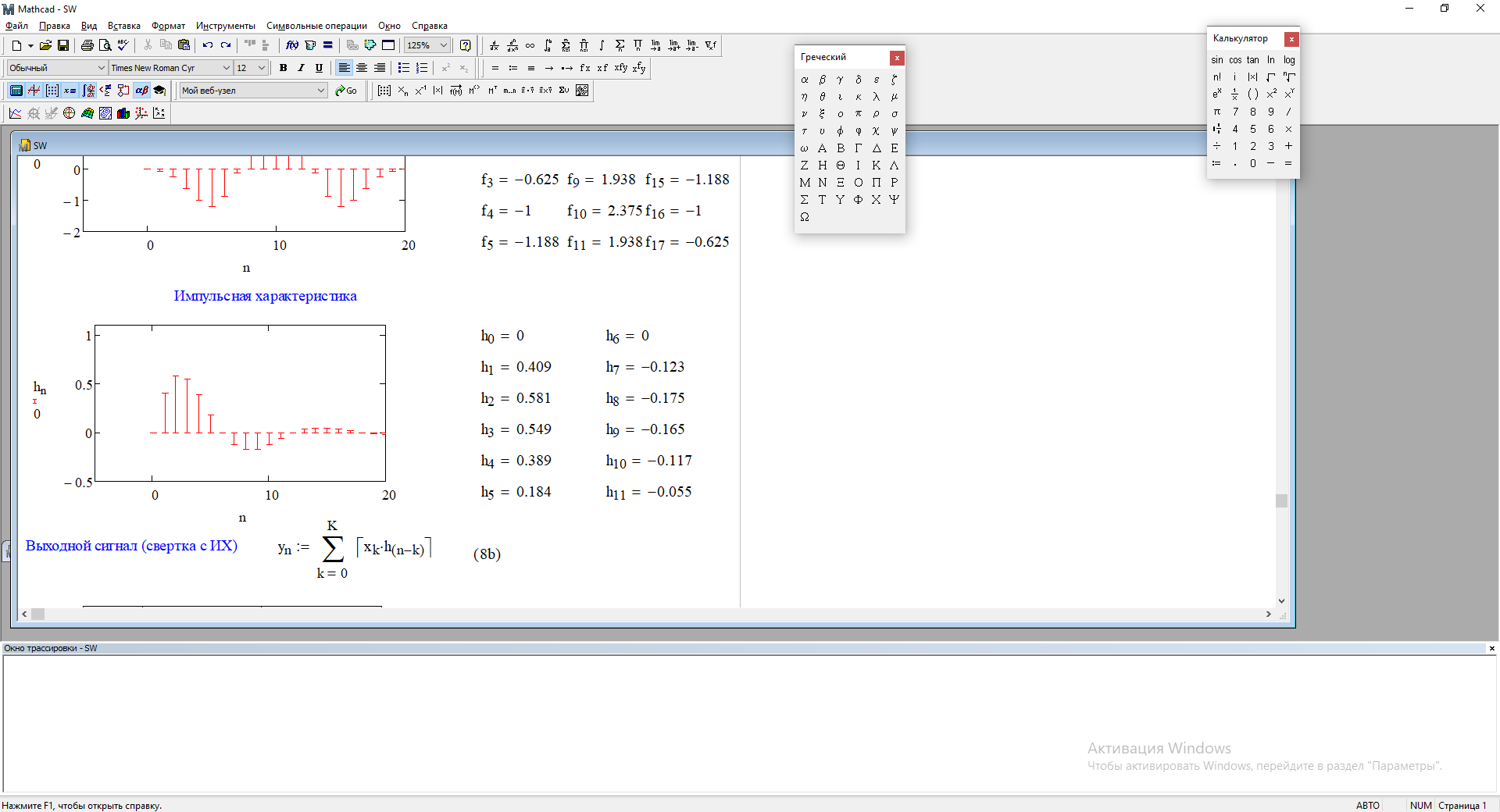 Рис. 4.6 – Импульсная характеристика Дискретная свёртка данного сигнала с импульсной характеристикой: 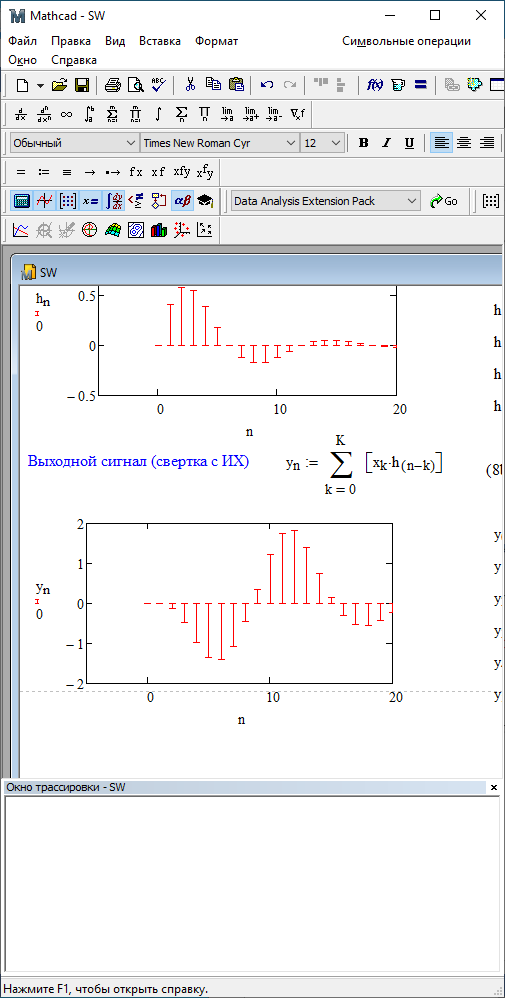 . Рис. 4.7 – Дискретная свертка с ИХ. 5. Зависимость дисперсии шума квантования АЦП на выходе цифрового фильтра от коэффициента сглаживания K. Запишите выражение для системной функции H(z) и зарисуйте структурную схему ЦФ. Рассчитайте теоретически зависимость дисперсии шума квантования АЦП на выходе цифрового фильтра от коэффициента сглаживания K. Сравните расчет с полученными данными. Исследуем зависимость дисперсии шума квантования АЦП сглаживающего звена от коэффициента К. Структурная схема сглаживающего звена приведении на Рис.5.1: 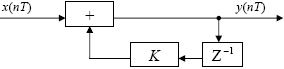 Рис.5.1 – Структурная схема сглаживающего звена. Системная функция сглаживающего звена: 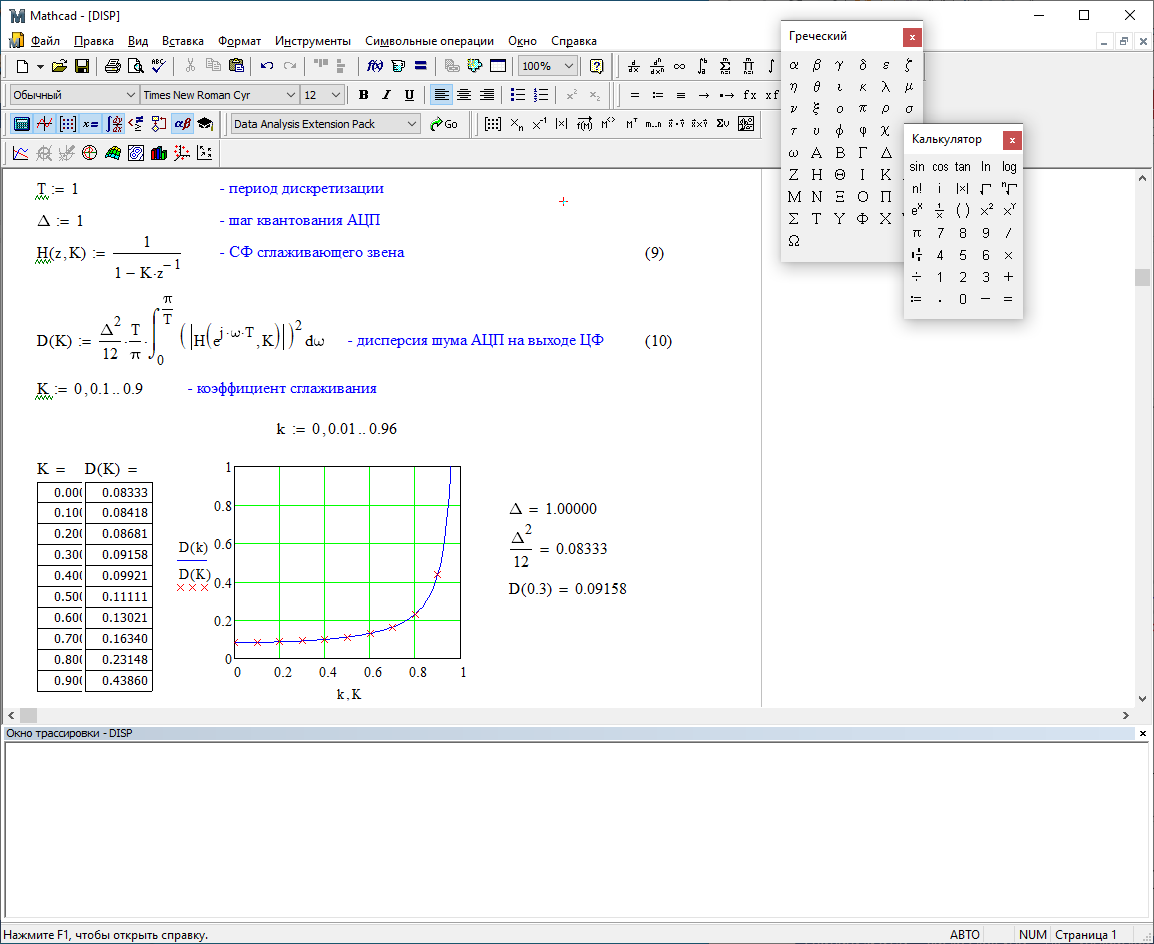 Рис. 5.1 – График зависимости дисперсии от коэффициента сглаживания К. Рассчитаем теоретически зависимость дисперсии шума квантования АЦП на выходе цифрового фильтра от коэффициента сглаживания K: 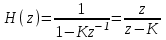 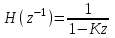 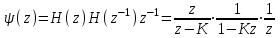 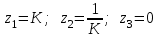 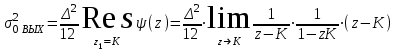 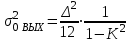 Расчетные и экспериментальные данные сведены в таблицу 5.1. Таблица 5.1
Можно заметить, что эти данные, с большой степенью точности совпадают. 6. Просмотрите поля ошибок, вычисленные программными модулями graf1, graf2, graf3. Зарисуйте эти поля ошибок и объясните функциональные зависимости от значений коэффициентов b1 и b2. Разностное уравнение без сохранения остатков : 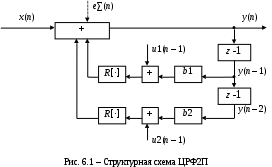 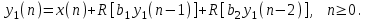 Разностное уравнение с сохранением остатков: 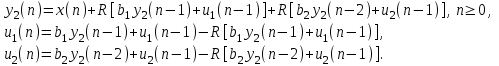 Дисперсия ошибки вычислений на выходе фильтра: 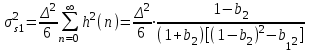 . .Дисперсия ошибки при сохранении остатков: 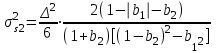 Эффективность метода при сохранении остатков можно определить с помощью отношения дисперсий: 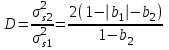 . .Графически дисперсии ошибок 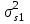 и и 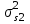 можно представить в виде полей на «треугольнике устойчивости» (рис. 6.2). Плоские части соответствуют усилению ошибок. можно представить в виде полей на «треугольнике устойчивости» (рис. 6.2). Плоские части соответствуют усилению ошибок.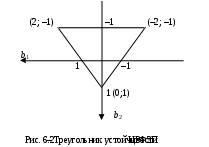 Двумерное поле ошибок округления в ЦФ второго порядка без учета остатков в зависимости от значений коэффициентов фильтрации В1 иВ2: 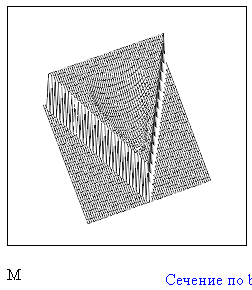 Рис.6.3 – Двумерное поле ошибок округления в ЦФ второго порядка без учета остатков в зависимости от значений коэффициентов фильтрации В1 иВ2. Разрезы двумерного поля ошибок в зависимости от значений коэффициентов  . .b1=0; b2=0 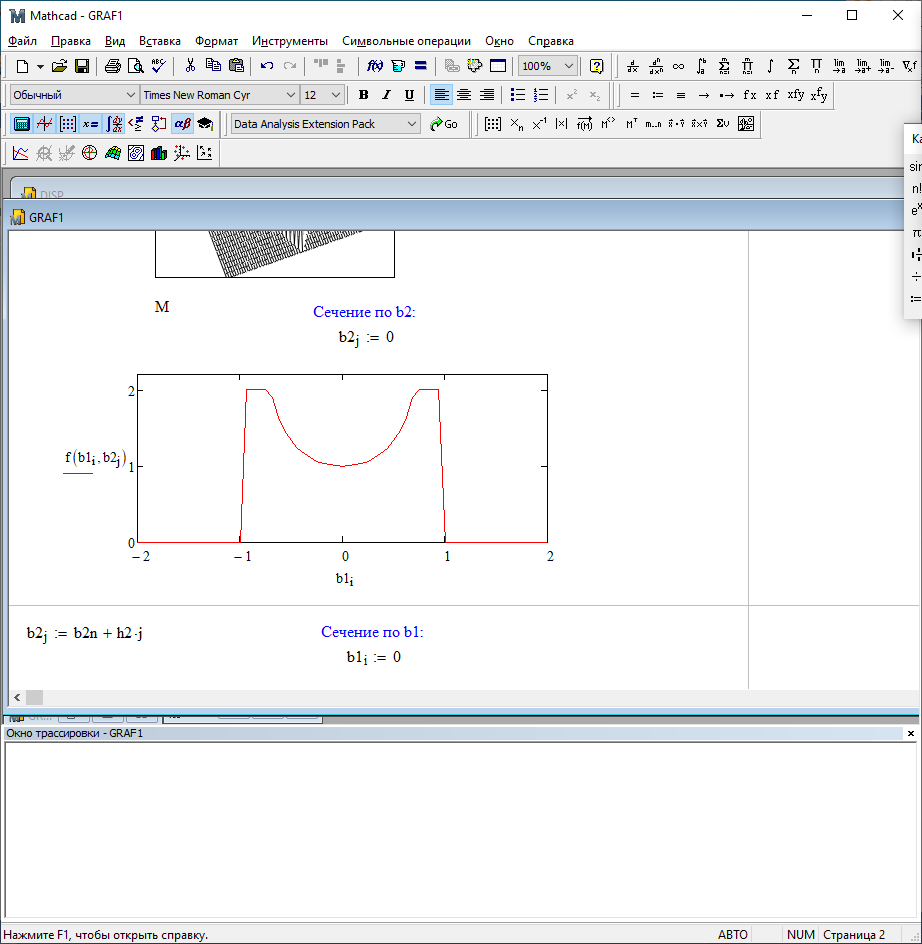 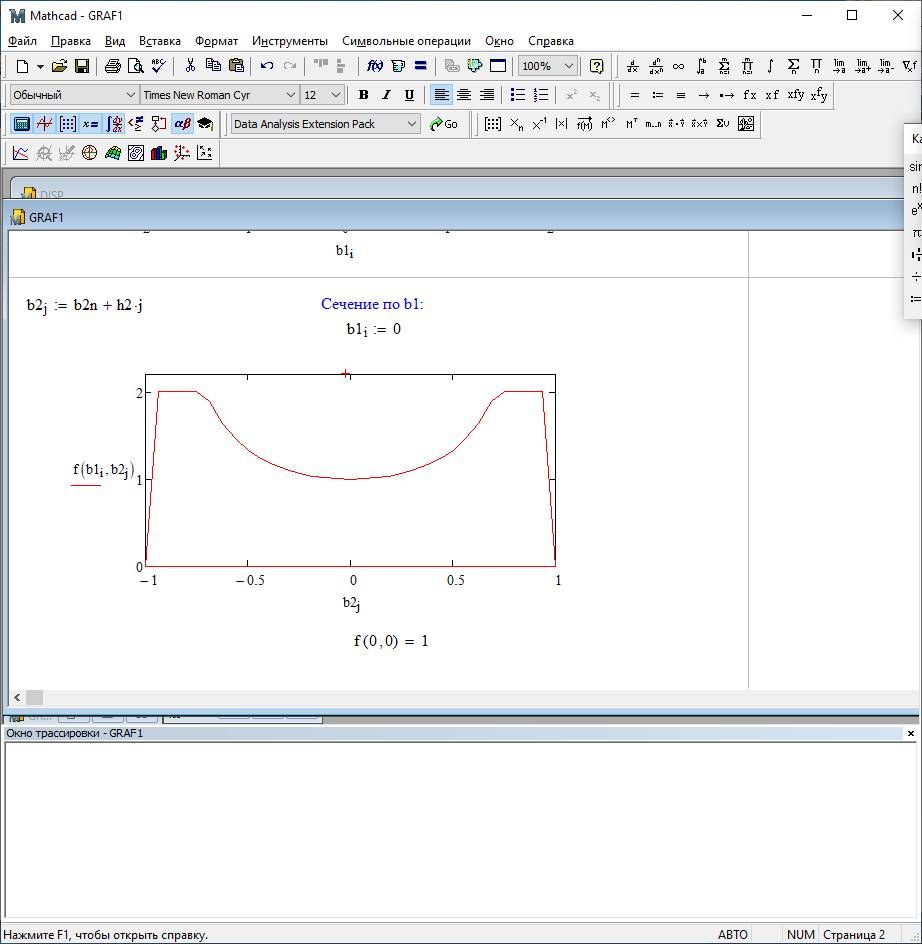 b1=0; b2=0,5 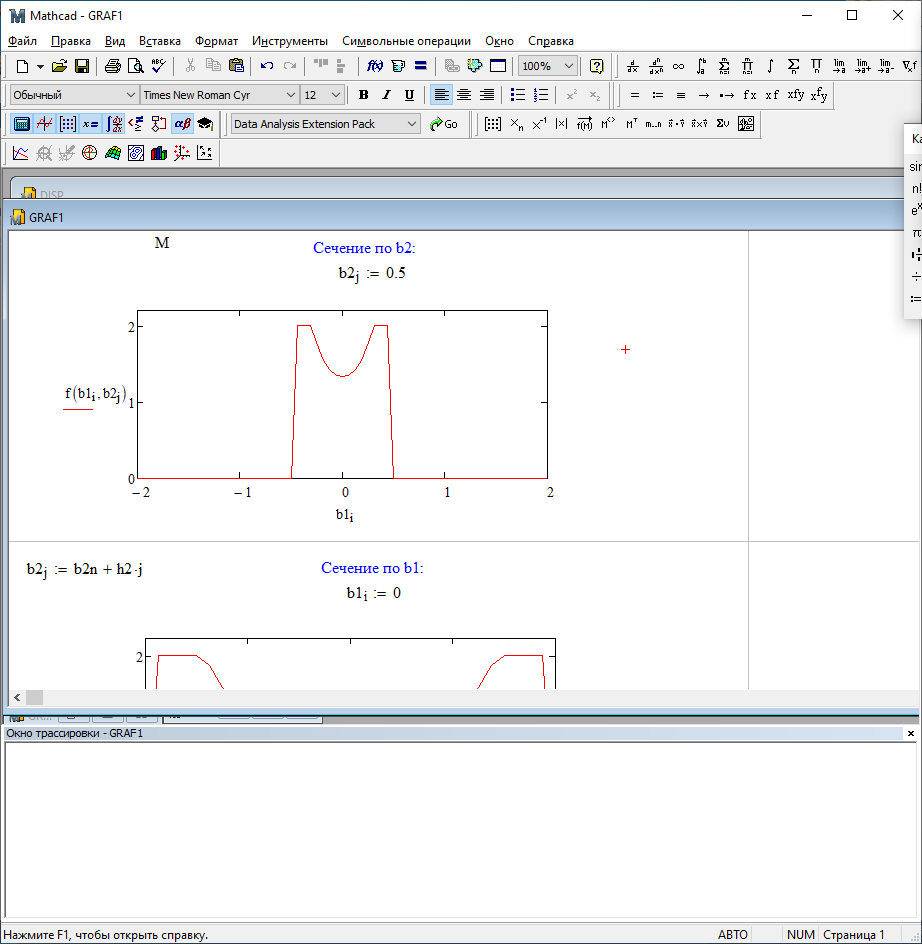 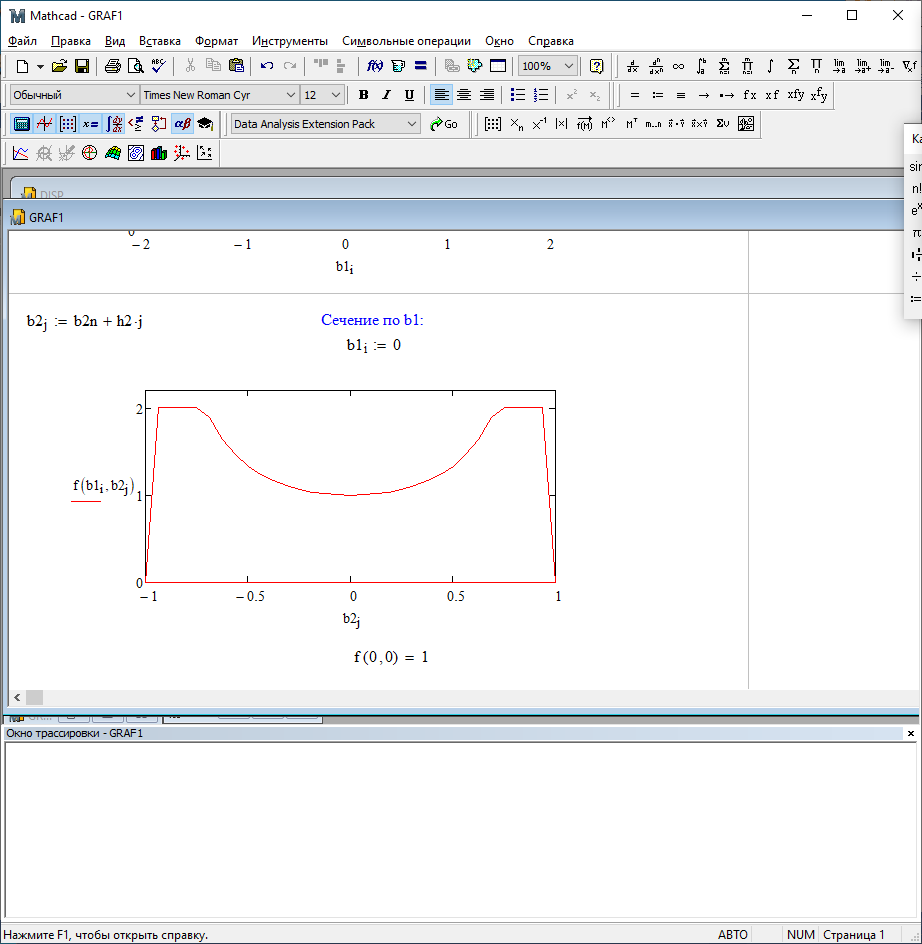 b1=0; b2=-0,5 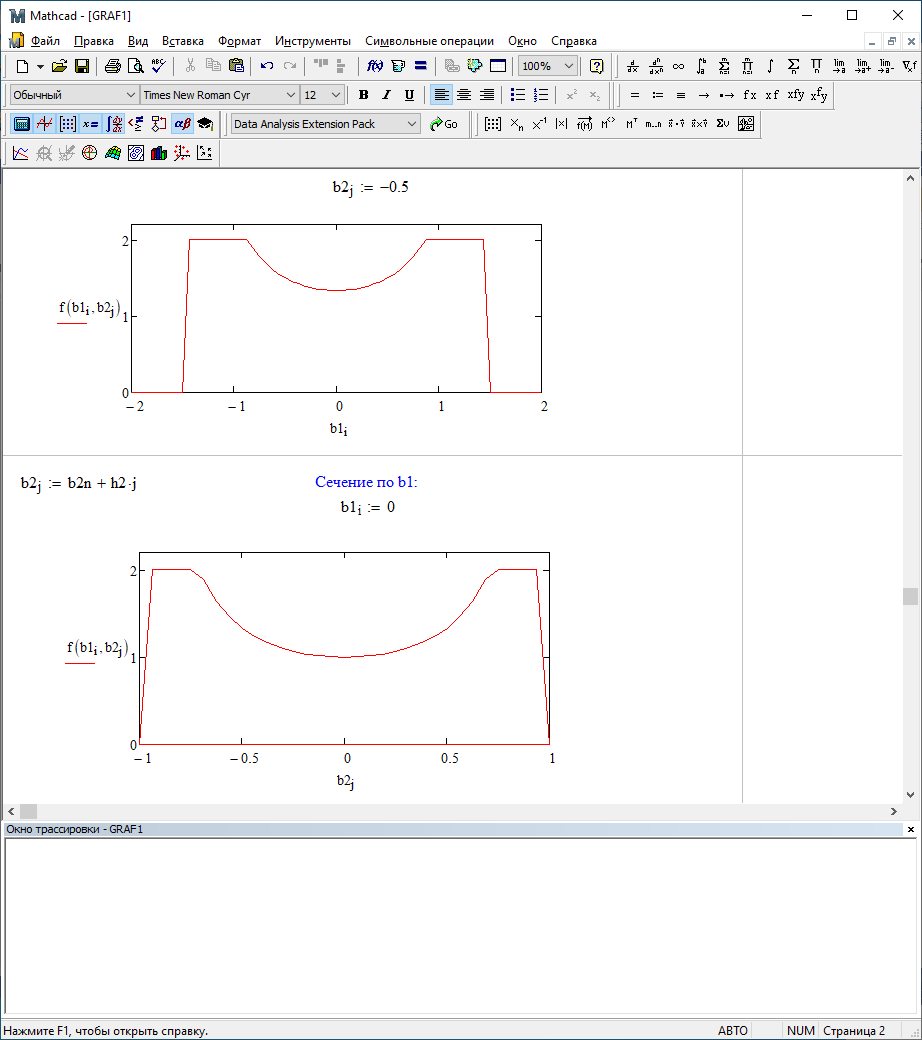  b1=0,5; b2=0 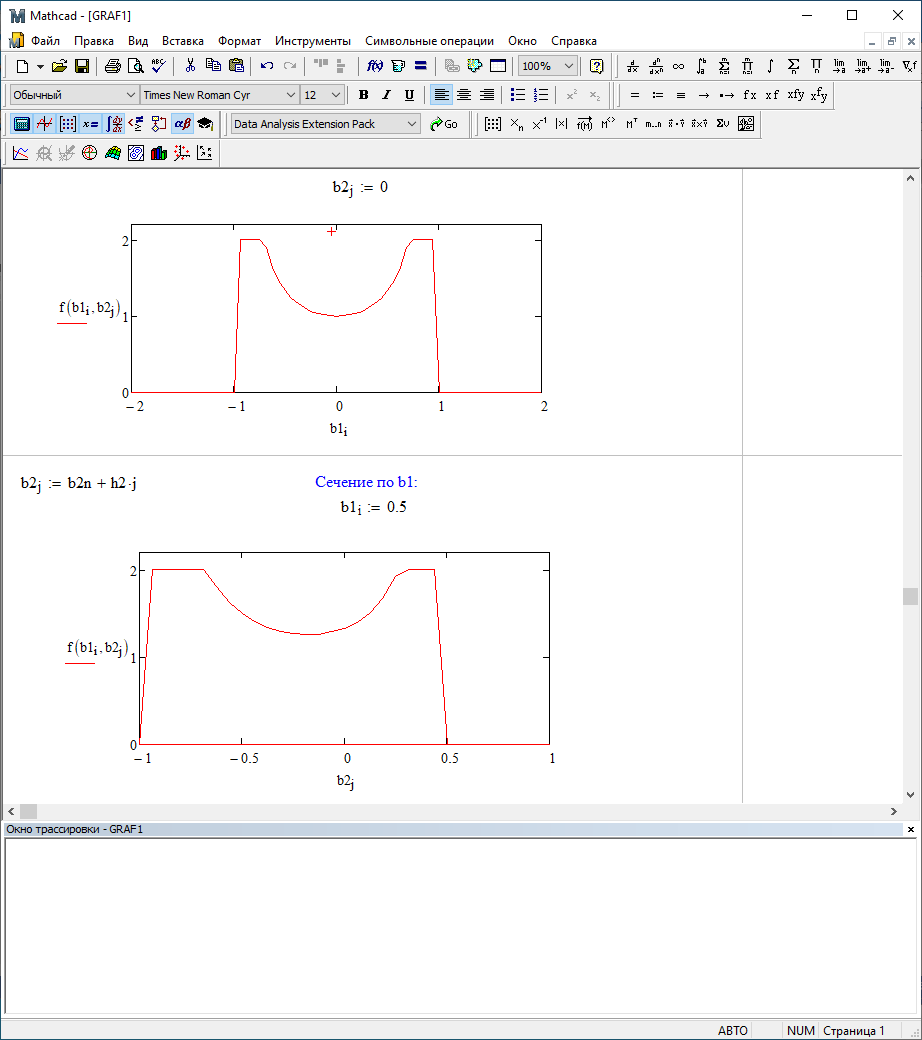  b1=-0,5; b2=0 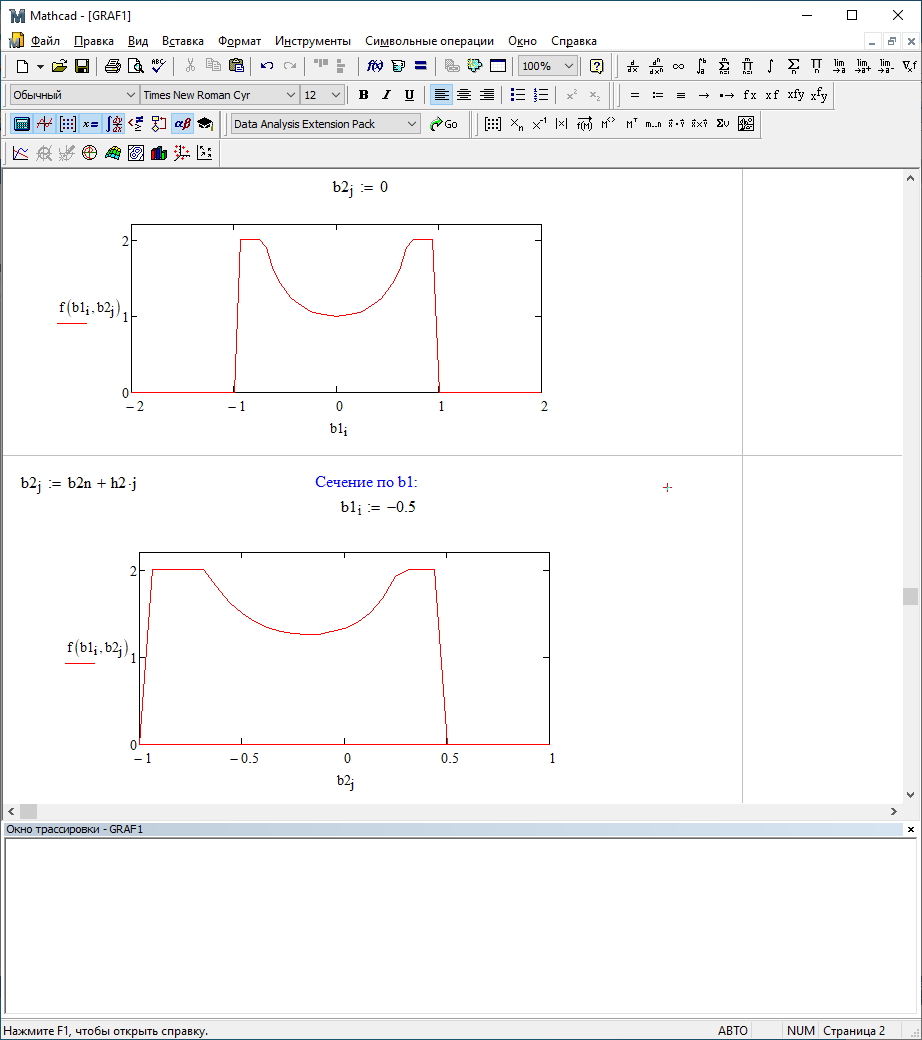  b1=0,9; b2=0,9   Двумерное поле ошибок округления в ЦФ второго порядка с учётом остатков в зависимости от значений коэффициентов фильтрации В1 иВ2:  Рис.6.4 – Двумерное поле ошибок округления в ЦФ второго порядка с учетом остатков в зависимости от значений коэффициентов фильтрации В1 и В2. Разрезы двумерного поля ошибок в зависимости от значений коэффициентов 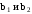 . .b1=0; b2=0 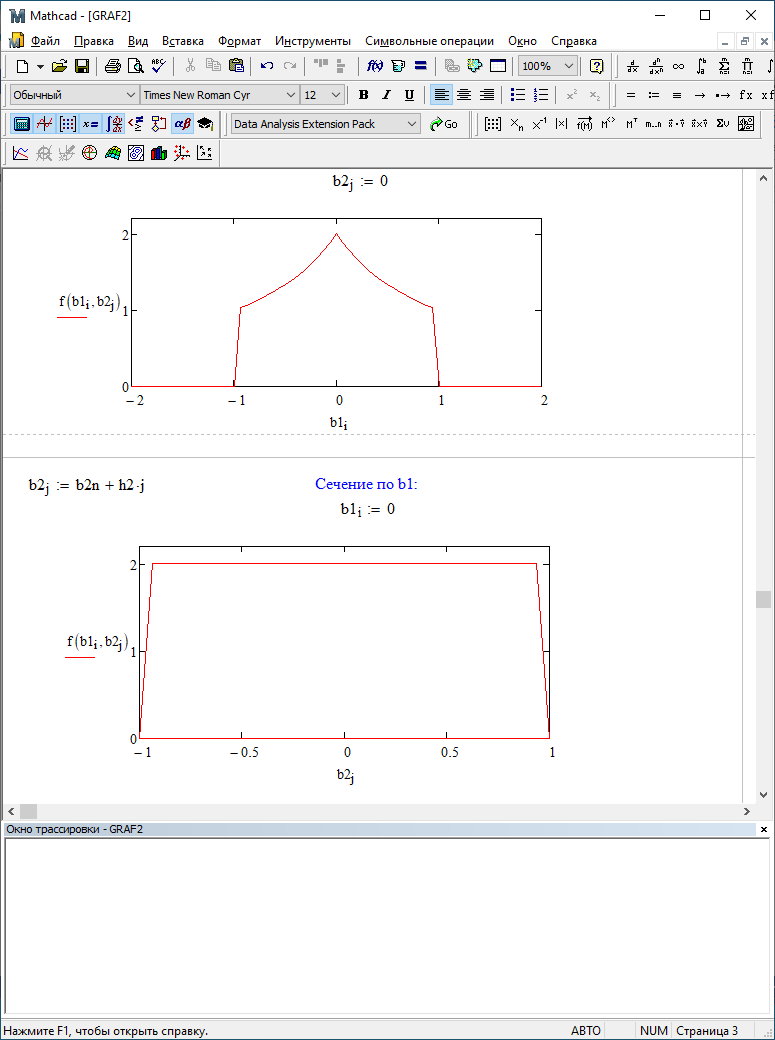  b1=0; b2=0,5 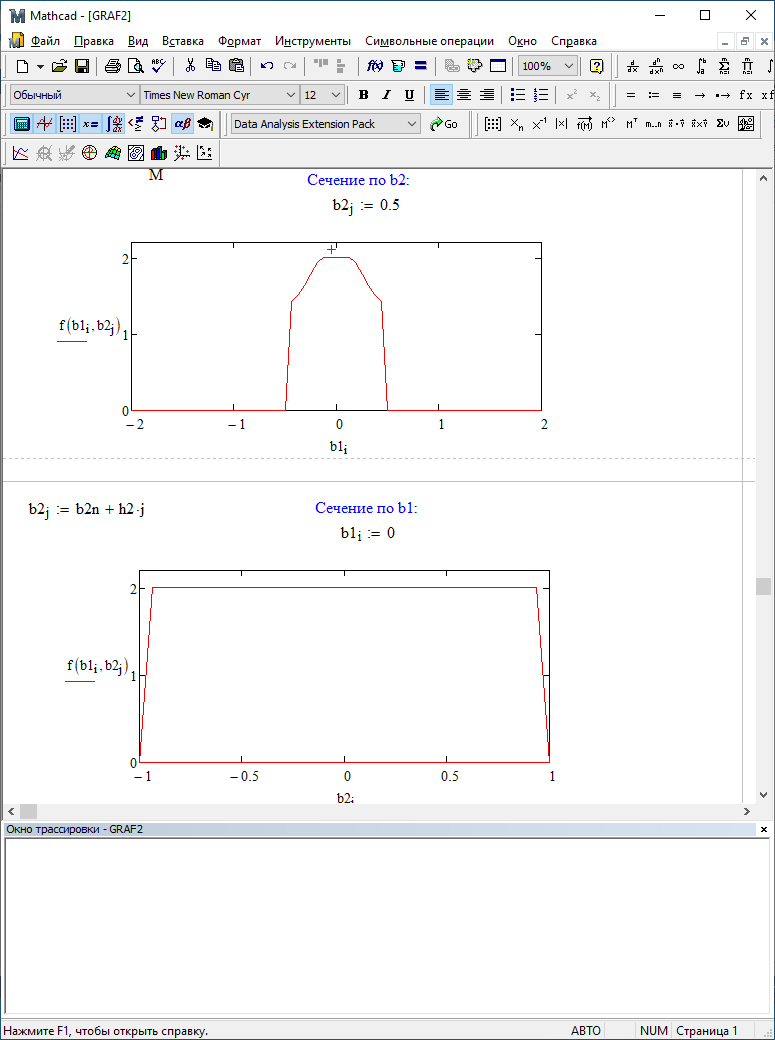  b1=0; b2=-0,5 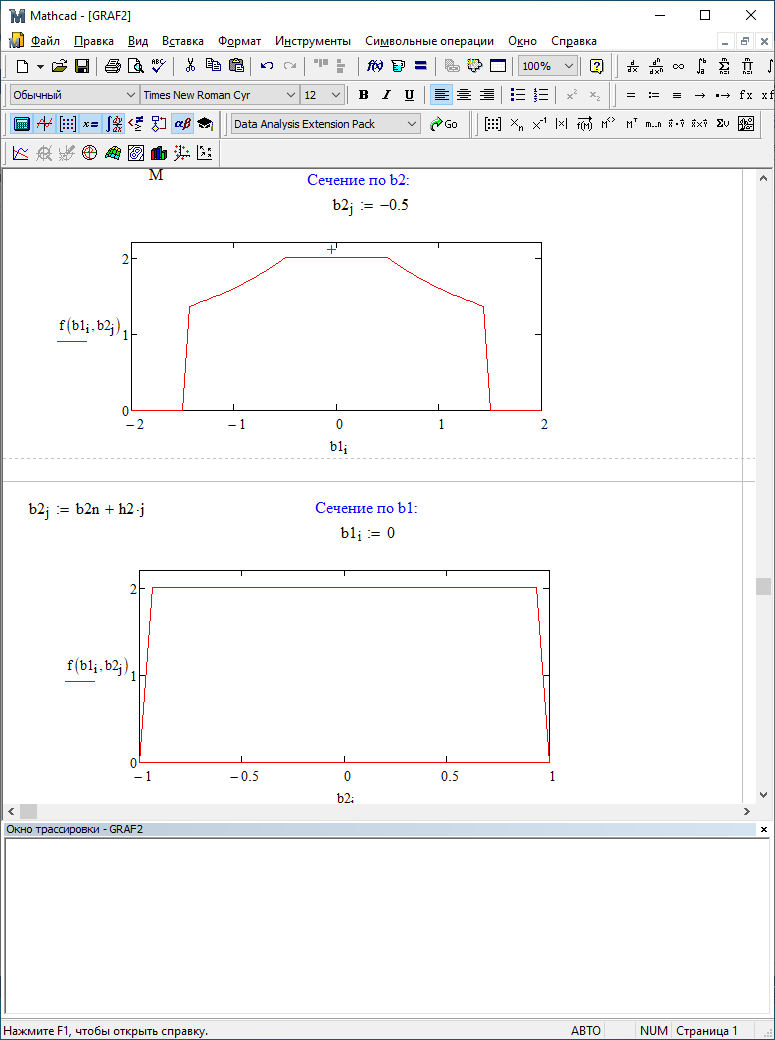  b1=0,5; b2=0 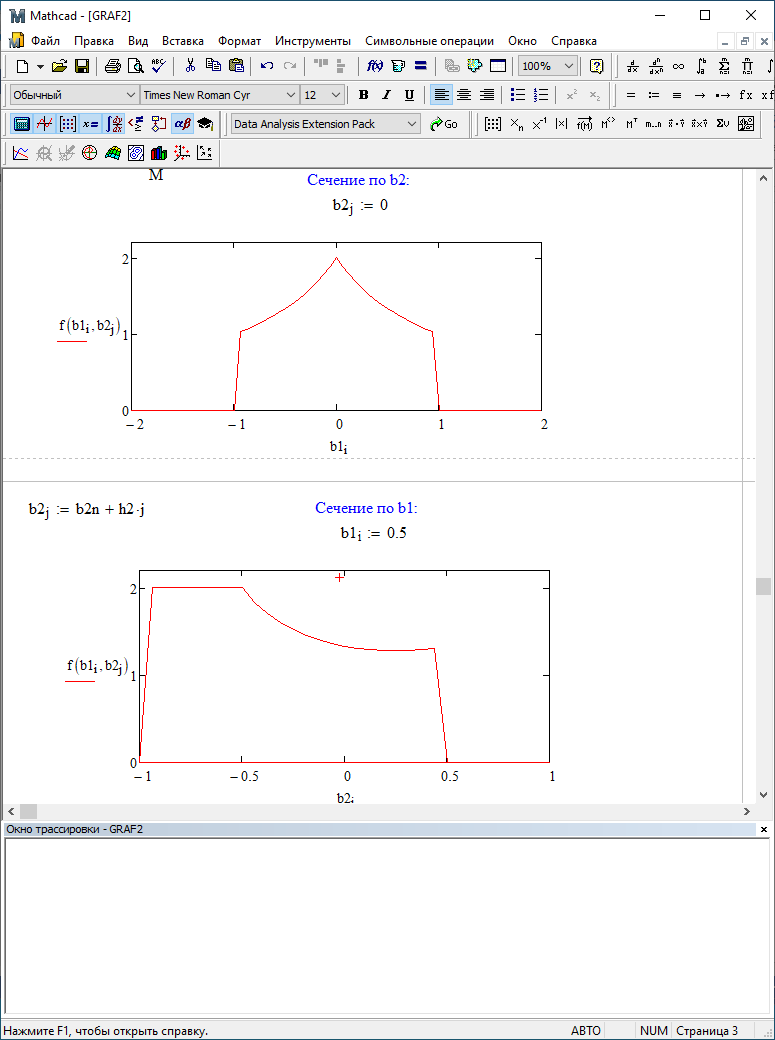  b1=-0,5; b2=0 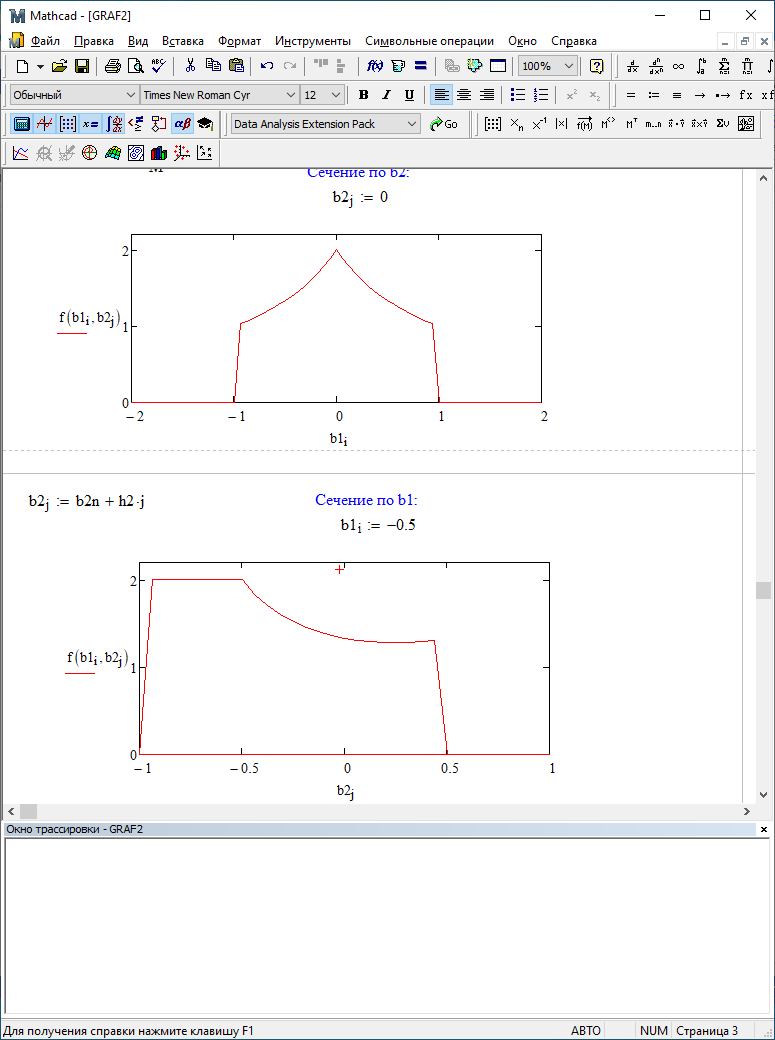  b1=0,9; b2=0,9 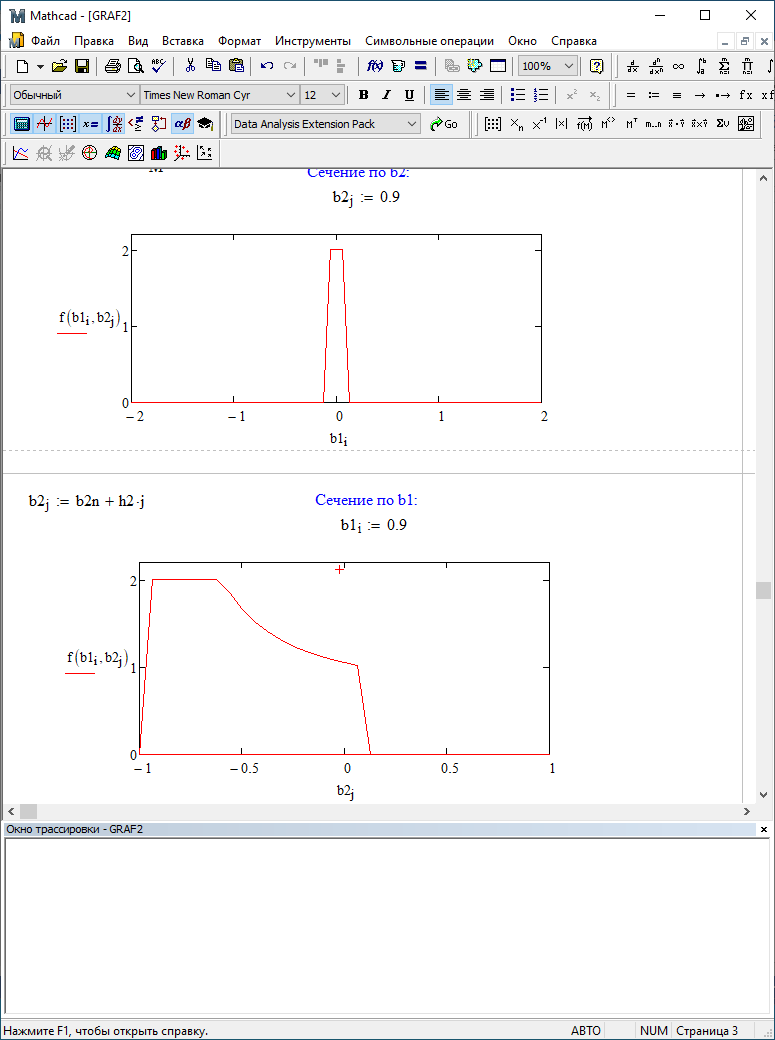  Двумерное поле относительной дисперсии ошибок для двух вариантов построения ЦФ второго порядка:  Рис.6.5 – Двумерное поле относительной дисперсии ошибок для двух вариантов построения ЦФ второго порядка. Разрезы двумерного поля ошибок в зависимости от значений коэффициентов 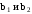 . .b1=0; b2=0 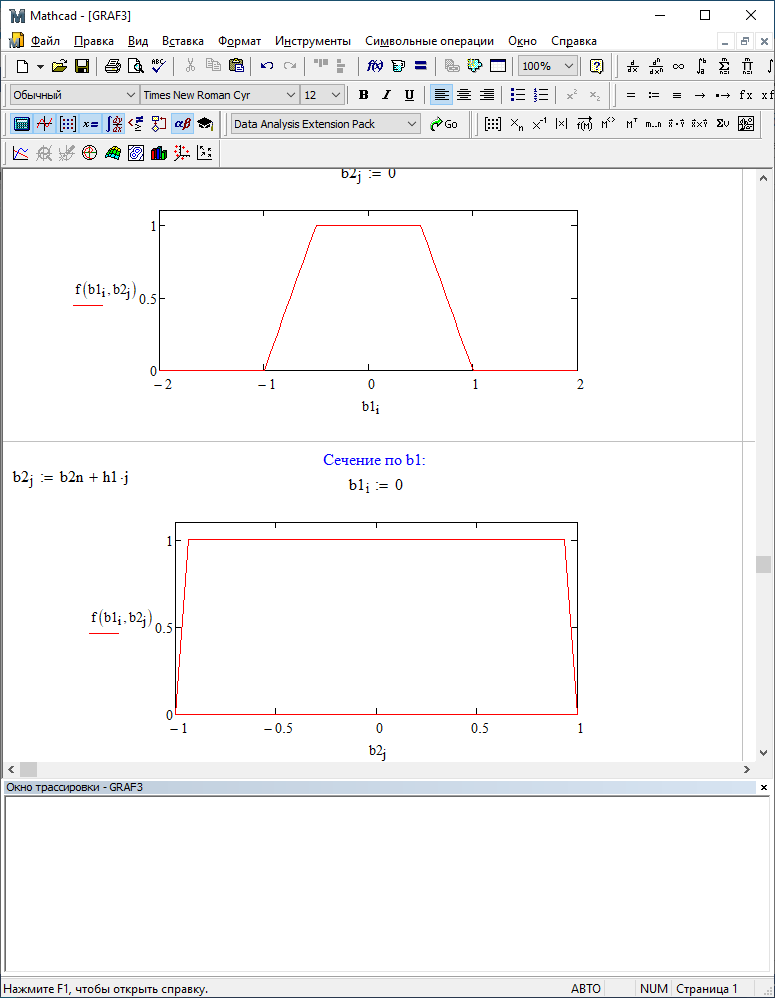  b1=0; b2=0,5 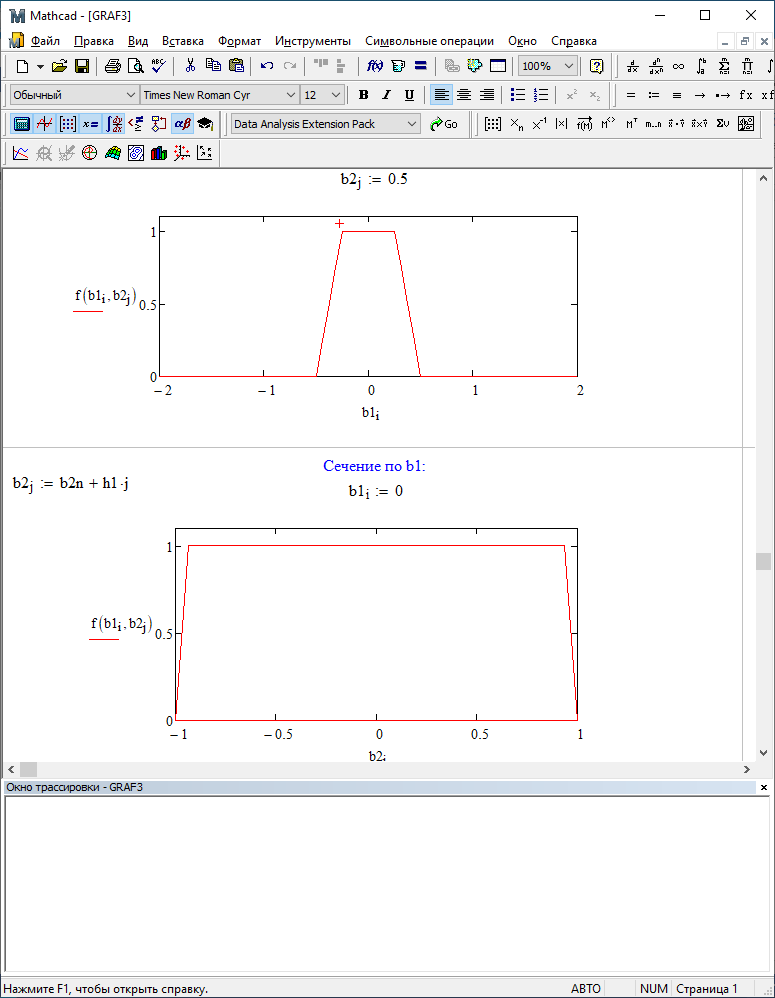  b1=0; b2=-0,5 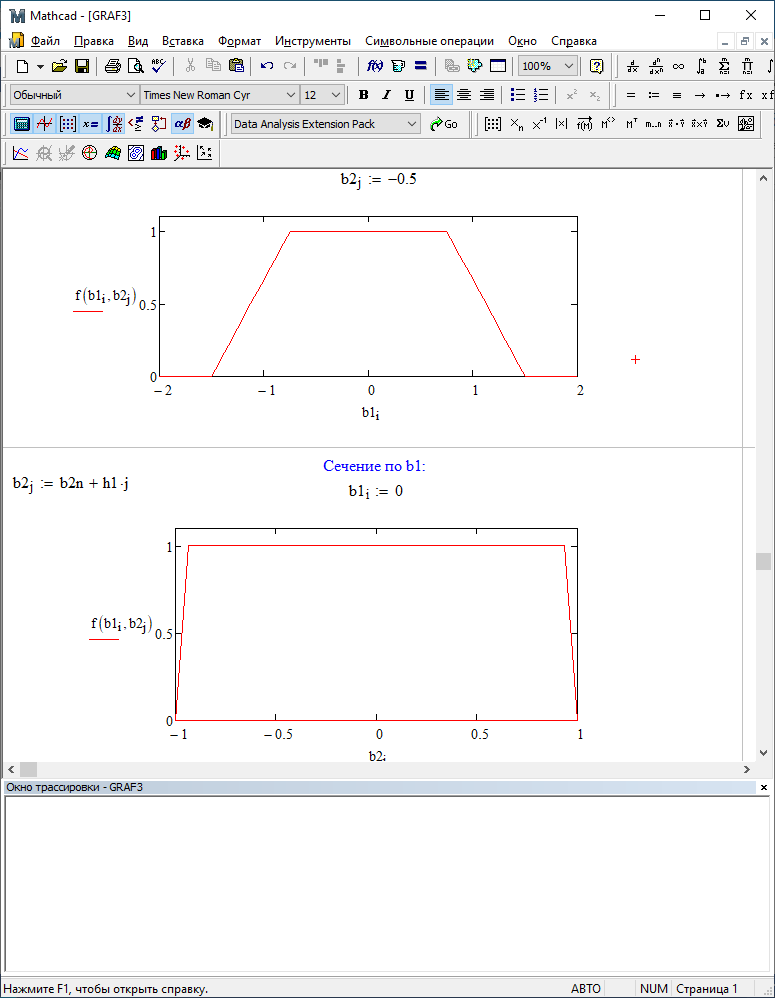  b1=0,5; b2=0 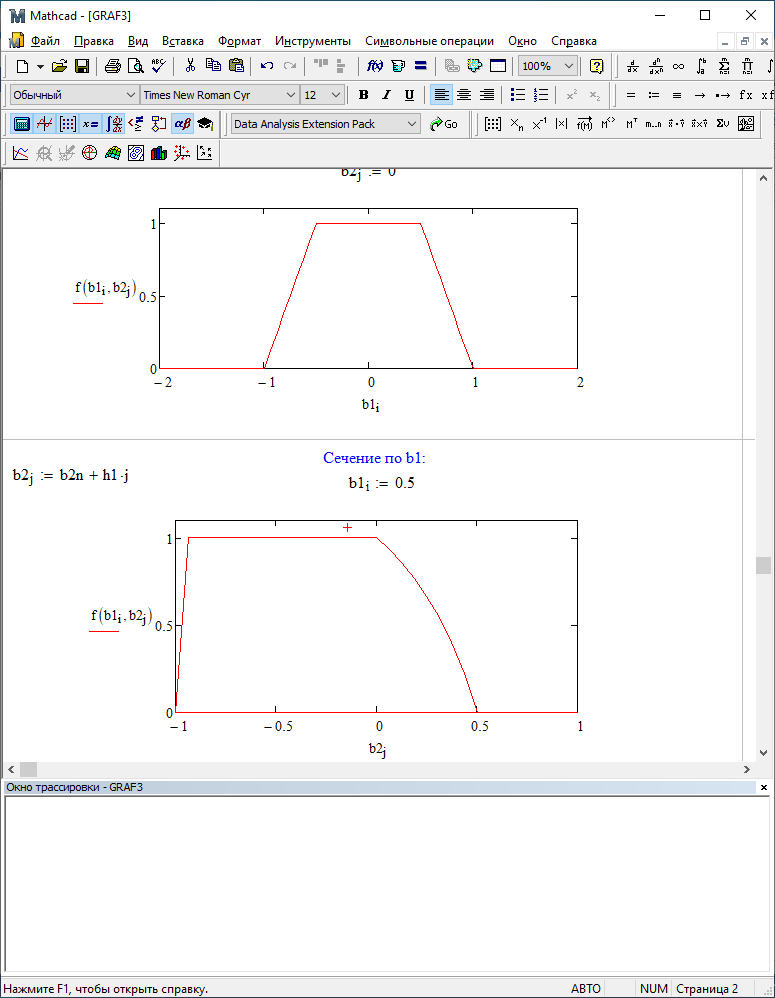  b1=-0,5; b2=0 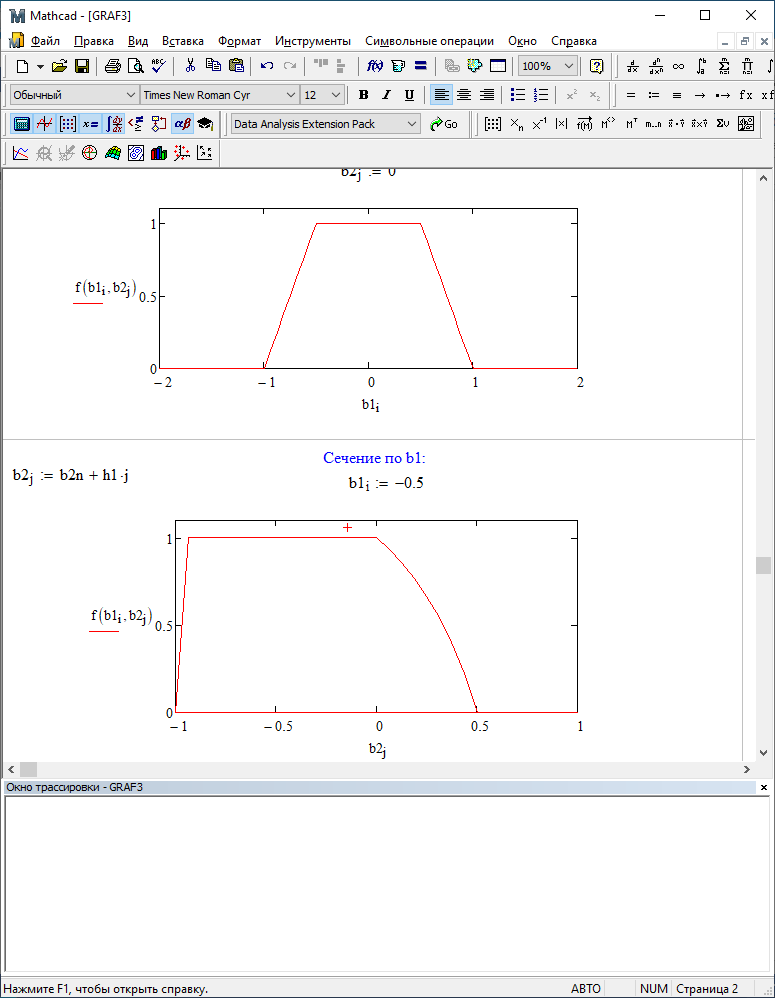  b1=0,9; b2=0,9 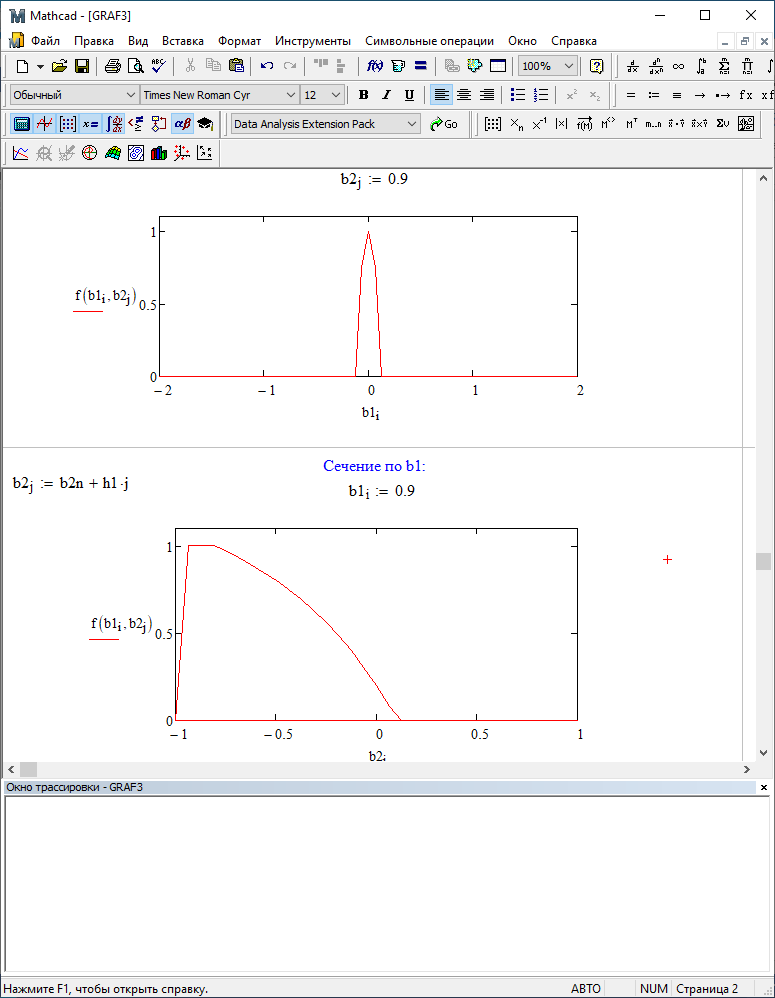  Таким образом, можно заметить, что выигрыш происходит на наклонных участках |b1| > 0,5. В этих областях предпочтительнее фильтр с использованием остатков, а на плоских областях лучше использовать фильтр без учета остатков. 7. Выводы В данной лабораторной работе были построены ИХ и ПХ, АЧХ и ФЧХ для различных цифровых фильтров. Полученные характеристики цифровых фильтров полностью соответствуют характеристикам своих аналоговых фильтров-прототипов, что говорит о возможности применения ЦФ для фильтрации. Также были построены вышеперечисленные характеристики для режекторного фильтра. При уменьшении коэффициента b1 до 0,177 в ИХ и ПХ изменился только первый отсчет. Стал выше, вследствие того, что мы увеличили а0. АЧХ фильтра поднялась с 1 до 1.2 на нижних и верхних частотах (рис. 2.8). ФЧХ фильтра изменилась значительно. В области средних частот характеристика сильно исказилась. Появился «прогиб» характеристики вверх и вниз (рис. 2.9). Было рассчитаны значения дисперсии. Можно сделать вывод о том, что значения, полученные экспериментальным путем, отличаются от теоретических с допустимой погрешностью. Было рассмотрено двумерное поле ошибок округления в ЦФ второго порядка без учета остатков в зависимости от значений коэффициентов фильтрации В1 иВ2 При их увеличении происходит значительное уменьшение площади двумерного поля ошибок. Плоские части соответствуют усилению сшибок. Для двумерного поля ошибок округления в ЦФ второго порядка с учётом остатков в зависимости от значений коэффициентов фильтрации В1 иВ2 видно также явное уменьшение площади поля ошибок, при увеличении b1 и b2. Явно выражено более грубое «урезание» сечения поля ошибок, по сравнению с полем ошибок без учета остатков. Анализируя изменение поля отношения дисперсий от изменения коэффициентов, можно предположить, что выигрыш происходит на наклонных участках |b1| > 0,5. В этих областях предпочтительнее фильтр с использованием остатков, а на плоских областях лучше использовать фильтр без учета остатков. |