АНАЛИЗ И ПРОГНОЗ ДИНАМИКИ ЦЕН НА ТОВАРЫ И УСЛУГИ НА ПРИМЕРЕ СРЕДНЕЙ ЦЕНЫ НА НЕДВИЖИМОСТ. Планирование и прогнозирование курсовая Журавлева. анализ и прогноз динамики цен на товары и услуги на примере средней цены на недвижимость
 Скачать 300.32 Kb. Скачать 300.32 Kb.
|
1 2 Глава 2. Анализ динамики индекса цен на первичном рынке жилья по РФ и ее прогнозирование на период 2021 – 2023 гг.2.1. Анализ динамики индекса цен на квартиры на первичном рынке жилья в РФ за 2008 – 2020 гг.Проанализируем динамику индекса цен на квартиры на первичном рынке жилья в РФ за 2008 – 2020 гг. Исходные данные РОССТАТ представлены в таблице 2.1. Таблица 2.1 – Индексы цен за 1 кв. м на все типы квартир на первичном рынке жилья за период 2008 – 2020 гг.
Произведем расчет абсолютных приростов, темпов роста и прироста по цепной и базисной схемам. Расчет индикаторов динамики индекса цен за 1 кв. м жилья на первичном рынке за 2009-2020 гг. по цепной и базисной схемам сведем в таблицу 2.2. За базис примем значение индекса в 2009 г. (год начала кризиса). Также это значение удобно тем, что период 2010 – 2020 нечетный, что позволяет принять временную шкалу периода с условием Σt = 0. Таблица 2.2 - Индикаторы динамики индекса цен за 1 кв. м жилья на первичном рынке (переменная y) за 2009-2020 гг.
Как видно из таблицы yц не равна const, а ТПц также не постоянен, то для построения уравнения тренда остается использовать лишь полиномы 2 и 3 степеней, причем заведомо ясно, что полином 2 степени также недостаточно точен (ТПц не const), поэтому используем его для сравнения. Итак, в дальнейшем будем использовать 2 модели данного временного ряда, а именно: 1. Полином 2 степени y = a0 + a1y + a2y2, в дальнейшем y для полинома 2 степени будем обозначать, как y2 Параметры модели a вычисляем по формулам: 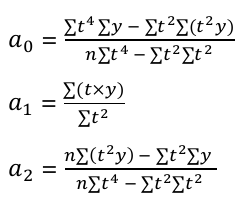 2. Полином 3 степени y = a0 + a1y + a2y2 + a3y3, в дальнейшем y для полинома 3 степени будем обозначать, как y3 Параметры модели a вычисляем по формулам: 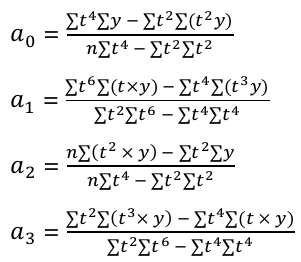 Построим таблицу для упрощения расчетов: Таблица 2.3 – Технические вычисления
С помощью данных, рассчитанных в таблице 2.3, получим параметры a для каждой модели: Полином 2 степени
Полином 3 степени
Следовательно: Таблица 2.4 – Исходные значения y, рассчитанные значения y2 и y3, для полиномов 2 и 3 степеней соответственно
На основании всей рассчитанной информации по обеим моделям построим общий график для y, y2, y3: 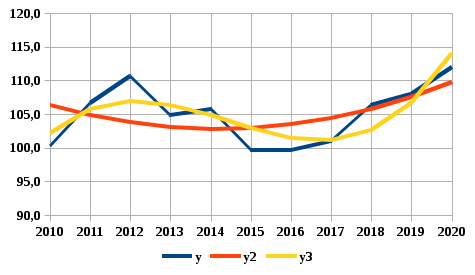 Рисунок 2.1 – Исходные y и рассчитанные y2 (полином 2 ст.) и y3 (полином 3 ст.) значения Визуально видно, что аппроксимация полиномом 3 степени более адекватно описывает исходную переменную у(t), но не будем полагаться на чувства, произведем точный расчет: Таблица 2.5 – Расчет стандартизированной ошибки аппроксимации
Следовательно, поскольку σ3 < σ2 более адекватной моделью является модель, основанная на полиноме 3 степени. 2.2. Прогнозирование индекса цен недвижимости и средней цены 1 кв. метра жилья на 2021 – 2023 гг Прогноз индекса цен на 3 года вперед (t = 6,7,8) осуществим на основе адекватной модели полинома 3 степени. Вводные данные: Достоверность Pдов = 95% n = 11 (количество наблюдений) m = 4 (параметры модели = коэффициентов полинома 3 степени) tα = 2.228 (коэффициент Стьюдента по таблице) Sy - остаточное среднее квадратическое отклонение, которое определяется по формуле: И Sy = 2.8, тогда доверительный интервал Δy = 6.2 Прогнозные значения индекса цен y(t) на 2021 – 2023 гг.: Таблица 2.6 – Прогнозные значения и max, min значения по доверительному интервалу с вероятностью 95%
И видим, что прогнозируемое значение индекса попадает в рассчитанный ранее доверительный интервал. Если же теперь вместо индекса рассмотреть средние цены за 1 м2 на первичном рынке жилья, то исходя из данных РОССТАТ: Таблица 2.7 – Средние цены за 1 кв. м на все типы квартир на первичном рынке жилья за период 2008 – 2020 гг.
можно провести абсолютно идентичные расчеты по данным таблицы 2.7 и получить прогнозные данные по средней цене на 2021 – 2023 гг. Таблица 2.8 – Прогнозные значения средней цены и max, min значения по доверительному интервалу с вероятностью 95%
Снова для аппроксимации полиномом 3 степени прогнозируемые значения с вероятностью 95% попадают в рассчитанный доверительный интервал. Выводы: с помощью стандартной расчетной процедуры было показано, что наиболее адекватной моделью для временных рядов индекса цен на недвижимость и средней цены за м2 является модель полинома 3 степени, дающей хороший прогноз с достаточно высокой степенью точности. ЗаключениеНа основании проведенного в работе исследования можно сделать следующие выводы: 1. За период 2008 – 2020 гг., средняя цена квадратного метра жилья на первичном рынке выросла более чем в полтора раза: с 52,504 до 79,003 тыс. руб. В среднегодовом выражении стоимость квадратного метра жилья в среднем росла на 3,46%, что в абсолютном выражении составило 2,208 тыс. руб. в год. 2. В работе была выдвинута гипотезу о том, что именно рост доходов населения является драйвером роста цен на первичном рынке недвижимости. Полученная в ходе исследования взаимосвязь между динамикой средних цен одного квадратного метра и доходами населения признается статистически адекватной при уровне значимости 0,1%. 3. Согласно трехзвенной скользящей средняя цена 1 квадратного метра жилья по итогам 2021 года составит 71,168 тыс. руб., что на 9,92% ниже уровня 2020 года, но на 11,1% выше цены 2019 года. Согласно уравнению линейного тренда, средняя цена 1 кв.. метра жилья по итогам 2021 года составит 67,849 тыс. руб., что на 14,12% ниже уровня 2020 года. В 2022 году, в сравнении с 2021 годом цена 1 кв. метра вырастет на 2,81% - до 69,754 тыс. руб., а в 2023 году – до 71,658 тыс. руб. А согласно уравнению параболы, средняя цена 1 кв.. метра жилья по итогам 2021 года составит 81,468 тыс. руб., что на 3,12% выше уровня 2020 года. В 2022 году, в сравнении с 2021 годом цена 1 кв. метра вырастет на 9,50% - до 89,208 тыс. руб., а в 2023 году – до 97,726 тыс. руб. (+9,55%). 4. Согласно уравнению линейного тренда, среднедушевой доход населения по итогам 2021 года составит 38,288 тыс. руб., в 2022 году – 39,906 тыс. руб., а в 2023 году – 41,524 тыс. руб. То есть, в 2021 году средняя цена одного квадратного метра жилья на первичном рынке составит 71,387 тыс. руб., в 2022 году – 74,178 тыс. руб., в 2023 году – 76,969 тыс. руб. Библиографический список1. Агапова Т.А. Макроэкономика: учебник / Т.А. Агапова, С.Ф. Серёгина. – М. : Московский финансово-промышленный университет «Синергия», 2018. – 560 c. 2. Статистика: учебное пособие для студентов, обучающихся по специальности «Финансы и кредит» и «Бухгалтерский учет , анализ и аудит» / Ю.С. Ивченко. – М.: РИОР: ИНФРА-М, 2016. – 374 с. 3. Статистика: учебник для бакалавров: учебник для обучающихся по специальности «Финансы и кредит» / И.И.Елисеева [и др.]; ред. И.И.Елисеева; ФИНЭК.- 3-е изд. перераб. и доп. – М.: Юрайт, 2016. – 558с. 4. Статистика: Учебное пособие / Под общ. ред. М.А. Абрамовой и Л.А. Александровой – М.: Кнорус, 2016. – 312 с. 5. Статистика: учебник для бакалавров: учебник для студентов вузов, обучающихся по специальности «Статистика» и др. экономических специальностей/ Л.И. Ниворожкина [и др.], ред. Л.И. Ниворожкина. - М.: Дашков и К, 2016. – 415 с. 6. Тарасевич, Л.С. Макроэкономика: Учебник для бакалавров / Л.С. Тарасевич, П.И. Гребенников, А.И. Леусский. - М.: Юрайт, 2019. – 543 c. 7. Тюрина А.Д. Макроэкономика: учебное пособие / А.Д. Тюрина, С.А. Шилина.– Саратов: Научная книга, 2019. – 259 c. 8. Шерстнева, Г. С. Социальная статистика. Конспект лекций: учеб. пособие / Г. С. Шерстнева. – М. : Эксмо, 2015. – 160 с. 9. Экономическая статистика: учебник для вузов / И.Д. Афанасенко [и др]; Под ред А.И. Добрынина; Л.С. Тарасевича.- Санкт –Петербург:Питер, 2016. –556 с. 10. Экономическая статистика: учебное пособие / коллектив авторов; под ред. В.М. Соколинского. – 6-е изд., перераб. и доп. – М.: КНОРУС, 2017. – 464 с. 11. Экономическая теория: учебник для студентов вузов, обучающихся по экономическим специальностям / [А.И. Балашов и др.]; под ред. Н.Д. Эриашвили. – М.:ЮНИТИ-ДАНА, 2019. – 527 с. 12. Федеральная служба статистики // Официальный сайт [Электронный ресурс]. – URL: http://www.gks.ru/ (дата обращения: 25.05.2021) 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
