Курсовая. Анализ и синтез плоских рычажных механизмов
 Скачать 179.01 Kb. Скачать 179.01 Kb.
|
3. СИЛОВОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМОВПри расчете механизма на прочность, жесткость и устойчивость необходимо знать значения и направления реакций в кинематических парах, их можно определить, построив план сил. В данный механизм входят ведущее звеноO1A и две группы Ассура 2-го класса CDи ABC. Начинаем рассматривать наиболее удаленную группу Ассура CD, вычерчиваем ее в том же положении и масштабе, как на схеме. Нагружаем эту группу Ассура всеми действующими на нее силами веса F4 и F5 (в центрах тяжести) и силами инерции FИ4; FИ5 - против ускорения 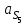 ;моментом пары сил ;моментом пары сил 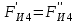 ; силой полезного сопротивления Fпс , которая приложена к звену d(S5) в направлении, противоположном скорости точки приложения (горизонтально влево). В тоску С F24. Представим эту реакцию в виде двух составляющих - ; силой полезного сопротивления Fпс , которая приложена к звену d(S5) в направлении, противоположном скорости точки приложения (горизонтально влево). В тоску С F24. Представим эту реакцию в виде двух составляющих - 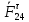 , направленной перпендикулярно к оси звена CD, и , направленной перпендикулярно к оси звена CD, и 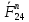 - вдоль звена CD. - вдоль звена CD. Вторую по удаленности группу Ассура AСВ вычерчиваем ее в том же положении и масштабе, как на схеме. Нагружаем эту группу Ассура всеми действующими на нее силами веса F3 и F2 (в центрах тяжести) и силами инерции FИ2 - против ускорения центра тяжести 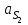 ; FИ3 - против ускорения ; FИ3 - против ускорения 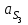 ; моментом пары сил ; моментом пары сил 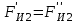 и силой и силой 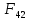 ,приложенной в точку С в противоположном направлении ,приложенной в точку С в противоположном направлении 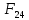 . .3.1 Определение силОпределение сил тяжести тяжести производится с помощью коэффициента q= 0,15 Н/мм, выражающего вес одного миллиметра длины звена в ньютонах (Н): 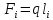 (3.1) (3.1)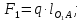 (3.2) (3.2)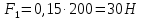 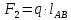 ; (3.3) ; (3.3)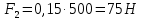 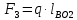 ; (3.4) ; (3.4)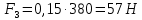 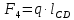 ; (3.5) ; (3.5)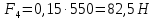 В составе механизма есть ползун, для определения силы тяжести воспользуемся следующей формулой: F5=1000  q (3.6) q (3.6)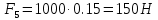 ; ;Определяем массу каждого звена, кг: 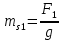 ; (3.7) ; (3.7)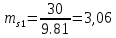 кг; кг;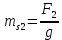 ; (3.8) ; (3.8)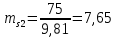 кг; кг;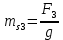 ; (3.9) ; (3.9)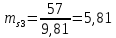 кг; кг;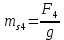 ; (3.10) ; (3.10)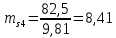 кг; кг;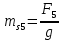 ; (3.11) ; (3.11)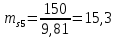 кг; кг;Определяем силу инерции каждого звена, Н: 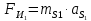 ; (3.12) ; (3.12)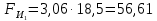 Н; Н;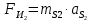 ; (3.13) ; (3.13)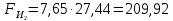 Н; Н;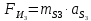 ; (3.14) ; (3.14)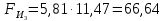 Н; Н;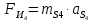 ; (3.15) ; (3.15)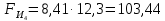 Н; Н;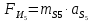 ; (3.16) ; (3.16)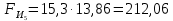 Н; Н;Определяем момент пары сил инерции для звеньев АВ, CD совершающих сложные движения: звено СD – 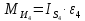 ; (3.17) ; (3.17)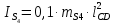 ; (3.18) ; (3.18)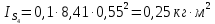 ; ;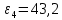 c-2. c-2.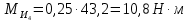 ; ;звено AB – 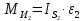 ; (3.19) ; (3.19)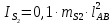 ; (3.20) ; (3.20)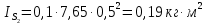 ; ;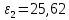 c-2. c-2.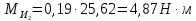 . .Силовой расчет механизма начинаем с наиболее удаленной от ведущего звена группы Ассура 4 – 5 (CD), состоящей из звеньев 4 и 5. Группу CD вычерчиваем отдельно в масштабе схемы механизма и в том же положении. Прикладываем к ней вместо связей две реакции: F34 представляем в виде двух составляющих: тангенциальной 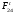 , направленной перпендикулярно к оси звена CD, и нормальной , направленной перпендикулярно к оси звена CD, и нормальной 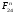 вдоль звена CD.. Кроме этого прикладываем силы веса F4 и F5 в центрах тяжести и силы инерции: вдоль звена CD.. Кроме этого прикладываем силы веса F4 и F5 в центрах тяжести и силы инерции: 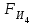 против ускорения тяжести S4 ; против ускорения тяжести S4 ; 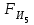 против ускорения против ускорения 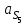 . Момент инерции . Момент инерции 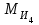 заменяем парой сил: заменяем парой сил: 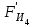 , приложенной в точке С против направления углового ускорения звена 4 (4), и , приложенной в точке С против направления углового ускорения звена 4 (4), и 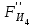 в точке D. в точке D. Для определения реакций в кинематических парах составляем векторное уравнение равновесия сил, действующих на группу 4 – 5 по порядку звеньев: 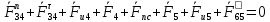 . (3.21) . (3.21)Силы 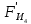 , , 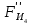 в уравнение не вписаны, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга, но для определения в уравнение не вписаны, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга, но для определения 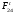 эти силы надо знать, Н: эти силы надо знать, Н: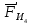 = =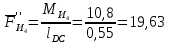 Определяем 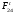 , входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено CD, относительно точки D.Зададимся правилом знака по часовой “+”,против часовой стрелки “-“: , входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено CD, относительно точки D.Зададимся правилом знака по часовой “+”,против часовой стрелки “-“: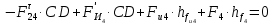 (3.22) (3.22)Отсюда 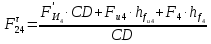 ; (3.23) ; (3.23)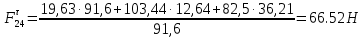 . .задаем масштаб плана сил: 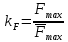 , Н/мм. (3.24) , Н/мм. (3.24)Максимальной силой является сила полезного сопротивления, которую в примере изобразим вектором длиной 200 мм. Получаем масштаб плана сил, Н мм-1: 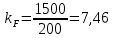 Н мм-1. Н мм-1.Вычисляем длины векторов, мм, изображающих эти силы, поделив их численные значения на масштаб: 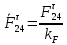 ; (3.25) ; (3.25)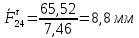 ; ;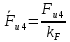 ; (3.26) ; (3.26)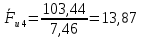 мм; мм; 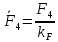 ; (3.27) ; (3.27)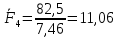 мм; мм;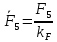 ; (3.28) ; (3.28) 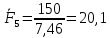 мм; мм; 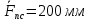 (задаемся) (задаемся)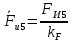 ; (3.29) ; (3.29) 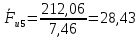 мм; мм;От произвольной точки а – начала плана сил параллельно силе 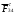 откладываем вектор откладываем вектор 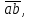 изображающий эту силу от конца вектора изображающий эту силу от конца вектора 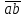 параллельно силе параллельно силе 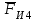 откладываем в том же направлении вектор откладываем в том же направлении вектор 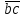 и далее векторы всех сил. Через точку l параллельно силе и далее векторы всех сил. Через точку l параллельно силе 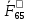 проводим линию действия проводим линию действия 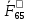 , а через точку a параллельно звену CD – линию действия силы , а через точку a параллельно звену CD – линию действия силы 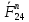 . Точка пересечения m этих линий определяет силы . Точка пересечения m этих линий определяет силы 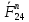 , , 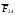 , , , , 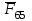 , Н: , Н: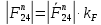 ; (3.30) ; (3.30)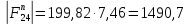 Н; Н;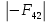 = = 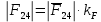 ; (3.31) ; (3.31)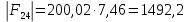 Н; Н;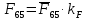 ; (3.32) ; (3.32)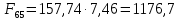 Н; Н;Далее следует отсоединить группу Ассура АВС, состоящую из звеньев 2 и 3, двух вращательных кинематических пар – А и В и одной поступательной (при движении ползуна по направляющей), вычертить ее в масштабе схемы. В соответствующих точках приложить действующие силы: 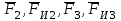 . Реакцию в шарнире А представить в виде двух составляющих – . Реакцию в шарнире А представить в виде двух составляющих – 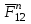 и и 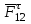 , а в поступательной паре – в виде F63, перпендикулярной линии хода ползуна. Реакцию со стороны звена 4 на звено 2, полученную из плана сил группы Ассура CD, , а в поступательной паре – в виде F63, перпендикулярной линии хода ползуна. Реакцию со стороны звена 4 на звено 2, полученную из плана сил группы Ассура CD, 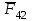 приложить в обратном направлении в точке С звена 2 приложить в обратном направлении в точке С звена 2 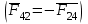 . .Составляем векторное уравнение равновесия сил, действующих на группу Ассура 2 – 3 (АВ), по порядку звеньев: 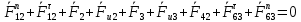 (3.33) (3.33)Силы 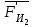 и и 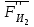 в уравнение не вписываем, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга. Но для определения в уравнение не вписываем, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга. Но для определения 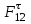 эти силы надо знать, определяем их: эти силы надо знать, определяем их: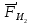 = =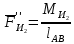 ; (3.34) ; (3.34) 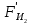 = =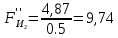 Н. Н.Звено O2B совершает качательное движение относительно оси, не проходящей через центр тяжести, поэтому перенесем силу инерции Fи3 в точку качания звена (точку K), расположенную на расстоянии O2K: O2K= 0,7 ∙ O2B = 0,7 ∙ 63,3 = 44,31 мм (3,35) Из уравнения моментов относительно точки В для звена 2 определяем составляющую 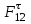 , Н: , Н: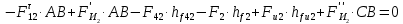 ; (3.36) ; (3.36)отсюда 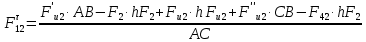 ; (3.37) ; (3.37)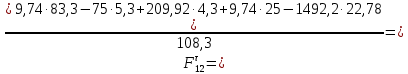 -299,47 Н. -299,47 Н.Размеры плеч 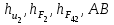 снимаем с чертежа в миллиметрах. Поскольку знак составляющей снимаем с чертежа в миллиметрах. Поскольку знак составляющей 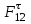 изменился, ее действительное направление не соответствует выбранному, следовательно, меняем его на противоположное изменился, ее действительное направление не соответствует выбранному, следовательно, меняем его на противоположноеИз уравнения моментов относительно точки В для звена 3 определяем составляющую 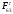 , Н , Н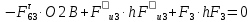 (3,38) (3,38)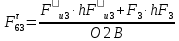 (3,39) (3,39)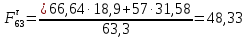 Н Н Выписав значения всех сил, действующих на группу Ассура, по максимальной из них задаемся масштабом: 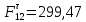 H; H; 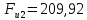 H; H; 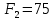 H; H; 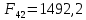 H; H;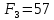 H; H; 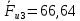 H: H: 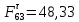 H HМаксимальную силу 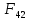 изобразим вектором, длина которого 200 мм (произвольно), тогда: изобразим вектором, длина которого 200 мм (произвольно), тогда: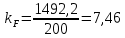 Н/мм. Н/мм.Вычисляем длины векторов, изображающих эти силы, мм:  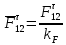 ; (3.40) ; (3.40) мм; мм;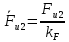 ; (3.41) ; (3.41)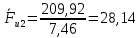 мм; мм;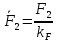 ; (3.42) ; (3.42)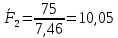 мм; мм;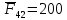 мм (задались); мм (задались);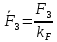 ; (3.43) ; (3.43)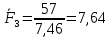 мм; мм;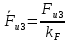 ; (3.44) ; (3.44)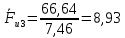 мм. мм.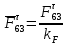 ; (3.45) ; (3.45)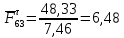 мм; мм;Строим план сил из которого определяем нормальную составляющую и результирующую давления в шарнире А и O2 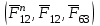 , Н: , Н: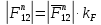 ; (3.46) ; (3.46)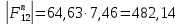 H; H;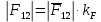 ; (3.47) ; (3.47)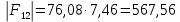 H; H;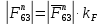 ; (3.48) ; (3.48)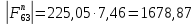 H; H;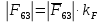 ; (3.49) ; (3.49)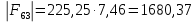 H; H;Расчет ведущего звена производим с учетом всех действующих на него сил: веса 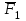 , инерции , инерции 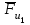 ,сила действующая звена 2 на звено 1 ,сила действующая звена 2 на звено 1 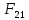 со стороны стойки – реакция со стороны стойки – реакция 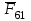 . Кроме этих сил в точку А кривошипа перпендикулярно к оси звена приложим уравновешивающую силу . Кроме этих сил в точку А кривошипа перпендикулярно к оси звена приложим уравновешивающую силу 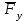 . Силы . Силы 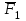 , ,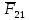 , ,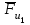 и и 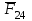 известны по значению и направлению, а силы известны по значению и направлению, а силы 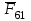 и и 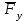 не известны. не известны.Для определения значения 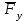 составляем уравнение моментов всех сил, действующих на звено 1, относительно точки О1: составляем уравнение моментов всех сил, действующих на звено 1, относительно точки О1: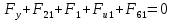 ; (3.50) ; (3.50)Из уравнения моментов относительно точки 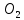 для звена 1 определяем составляющую для звена 1 определяем составляющую 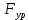 , Н: , Н: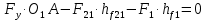 ; (3.51) ; (3.51)отсюда 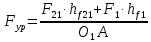 ; (3.52) ; (3.52)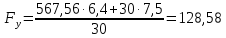 Н. Н. Определяем реакцию 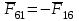 по значению и направлению путем построения плана сил согласно векторному уравнению: по значению и направлению путем построения плана сил согласно векторному уравнению: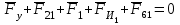 ; (3.53) ; (3.53)Выписав значения всех сил, Н, по максимальной из них задаемся масштабом: 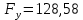 Н; Н; 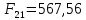 Н; Н; 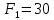 Н; Н; 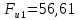 Н. Н.Изобразим F21 = 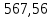 Н вектором длиной 100 мм, тогда: Н вектором длиной 100 мм, тогда: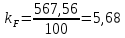 Н/мм. Н/мм.Вычисляем длины векторов всех сил для плана, мм: 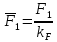 ; (3.54) ; (3.54)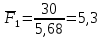 мм; мм;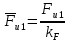 ; (3.55) ; (3.55)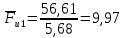 мм; мм;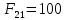 мм (задались); мм (задались);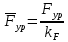 ; (3.56) ; (3.56)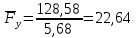 мм. мм.Соединив точки e и a получаем реакцию в шарнире О1 (со стороны звена 6 на звено 1): 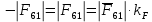 ; (3.57) ; (3.57)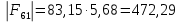 H. H. |
