Курсовая. Анализ и синтез плоских рычажных механизмов
 Скачать 179.01 Kb. Скачать 179.01 Kb.
|
3.2 Определение уравновешивающей силы методом рычага Жуковского.Соотношение между всеми действующими силами (кроме реакций), приложенными к звеньям механизма можно получить с помощью вспомогательного рычага Жуковского, сформулированного в теореме. Если план скоростей механизма, находящегося в равновесии, повернуть на 90, то механизм, рассматриваемый как твердое тело, вращающееся вокруг полюса плана и нагруженное теми же силами, приложенными в соответствующих точках плана, тоже находится в равновесии. Метод Жуковского можно применить для нахождения величины какой-либо силы, если точка приложения и линия действия заданы. Применим этот метод для нахождения уравновешивающей силы. Силы тяжести и инерции, приложенные в центрах масс, а также сила полезного сопротивления и уравновешивающая сила Fyр, приложенная в точке А и действующая перпендикулярно звену O1A. Повернем на 90° по часовой стрелке план скоростей механизма и в точки плана приложим соответствующие силы. Составим уравнение моментов сил относительно полюса РV, предварительно измерив все плечи сил, и найдем уравновешивающую силу, Н:  ; (3.58) ; (3.58)Отсюда  ; (3.59) ; (3.59)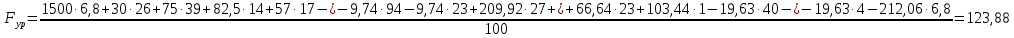 Н НПогрешность между расчетами уравновешивающей силы с помощью рычага Жуковского и постарением планов сил рассчитывается по формуле, %:  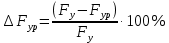 . (3.60) . (3.60) Подставляем числовые значения в формулу(3.44): 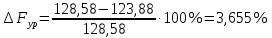 3.3 Кинематическое исследование механизмов методом графиков(кинематических диаграмм)Для того чтобы построить наглядное представление о характере движения какой-либо точки механизма, строят кинематические диаграммы перемещения, скоростей и ускорений точки. Кинематические диаграммы представляют собой графические зависимости перемещения S=f(t), скорости V=f'(t) и ускорения a=f "(t) исследуемой точки от времени поворота τ ведущего звена или S=f(φ1), V= f '(φ1) и a= f "(φ1) от угла поворота φ1 ведущего звена. Их построение после построения совмещенного плана положения механизма. В прямоугольной системе координат XOY откладываем по оси ординат перемещения точки B, по оси абсцисс - время одного цикла движения механизма. Разбиваем отрезок на 12 равных частей, из точек деления восстанавливаем перпендикуляры к оси абсцисс. На оси ординат откладываем отрезки перемещения SB точки. Из точек разметки оси ординат 1, 2, ..., 12 проводим прямые, параллельные оси абсцисс, до пересечения с соответствующим перпендикулярами. Соединив точки пересечения плавной линией, получаем диаграмму перемещений точки B механизма. Графически дифференцируя диаграмму перемещений, строим диаграмму скоростей точки B. Для этого проводим хорды кривой на соответствующих участках разметки и обозначаем их 1, 2, 3, ..., 12. В системе координат XOYпродолжаем ось абсцисс влево и на расстоянии H1=15 мм обозначаем полюс PV. Из полюса PV проводим лучи, параллельные этим хордам, до пересечения с осью ординат Y. Из точек пересечения лучей с осью Y проводим прямые, параллельные оси абсцисс, до середины между вертикалями. Соединив точки плавной кривой, получаем диаграмму скоростей точки B механизма. Графически дифференцируя диаграмму скоростей, получаем диаграмму ускорений точки B. Полюсное расстояние H2=15 мм. По построению диаграммы можно наглядно проследить за характером изменений кинематических параметров за полный цикл работы механизма и получить значения перемещения, скоростей и ускорений точки B через любой промежуток времени. |
