Курсовая. Анализ и синтез плоских рычажных механизмов
 Скачать 179.01 Kb. Скачать 179.01 Kb.
|
2.2. Построение планов положений механизмовПланом положения механизма называется чертеж, изображающий расположение его звеньев в какой-то определенный момент движения. Отсюда следует, что план положения представляет собой кинематическую схему механизма, вычерченную для заданного положения механизма. Планы положений механизмов, включающих в себя “двухповодковые” группы, строятся методом засечек. 2.3. Построение траекторий точекДля построения траектории какой-либо точки необходимо построить несколько планов положений механизма, найти на каждом из планов положение заданной точки и соединить их последовательно плавной пунктирной линией. Траектория кривошипа будет окружность радиуса О1А, траектория точки В будет прямая линия, траектория точки С замкнутая кривая в виде овала, траектория точки D дуга радиуса O2D. 2.4. Определение скоростей точек механизма методом планов скоростейЗная закон движения ведущего звена и длину каждого звена механизма, можно определить скорости его точек по значению и направлению в любом положении механизма путем построения плана скоростей для этого положения. Значения скоростей отдельных точек механизма необходимы при определении производительности и мощности машины, потерь на трение, кинематической энергии механизма; при расчете на прочность и решении других динамических задач. Построение планов скоростей и чтение их упрощаются при использовании свойств этих планов: 1) векторы, проходящие через полюс pV выражают абсолютные скорости точек механизма. Они всегда направлены от полюса. В конце каждого вектора принято ставить малую букву a, b, c, . . . s или другую, которой обозначена точка или шарнир механизма A, B, C, . . . S.Точки плана скоростей, соответствующие неподвижным точкам механизма, находятся в полюсе РV (О1, О2); 2) векторы, соединяющие концы векторов абсолютных скоростей, не проходящие через полюс, изображают относительные скорости. Направлены они всегда к той букве, которая стоит первой в обозначении скорости. 3) каждое подвижное звено механизма изображается на плане скоростей соответствующим одноименным, подобным и сходственно расположенным контуром, повернутым относительно схемы механизма на 90 в сторону мгновенного вращения данного звена. Это свойство плана называется свойством подобия и позволяет легко находить скорость точек механизма. Определяем абсолютные и относительные скорости точек звеньев и угловые скорости звеньев механизма для основного положения. Частота вращения кривошипа n = 130 об/мин; 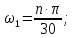 (2.2) (2.2) 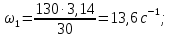 Находим скорость точки А кривошипа 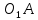 по формуле, м/с: по формуле, м/с: 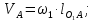 (2.3) (2.3)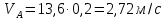 ; ;Вектор 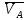 направлен перпендикулярно оси звена направлен перпендикулярно оси звена 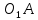 в сторону его вращения. Задаемся длиной отрезка в сторону его вращения. Задаемся длиной отрезка 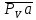 (произвольно), который на плане будет изображать скорость (произвольно), который на плане будет изображать скорость 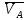 точки А; точки А;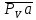 . Тогда масштаб плана скоростей, м/с мм: . Тогда масштаб плана скоростей, м/с мм: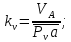 (2.4) (2.4) 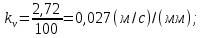 Из произвольной точки pV, в которой помещены и точки опор О1, О2, откладываем перпендикулярно к звену О1А отрезок РVа = 100 мм Для дальнейшего построения плана скоростей и определения скорости точки В составляем уравнение: 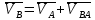 (2.5) (2.5)где 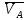 скорость точки А, известна по величине и направлению; скорость точки А, известна по величине и направлению;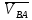 – относительна скорость точки В во вращении вокруг точки А. – относительна скорость точки В во вращении вокруг точки А.Относительная скорость 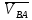 известна по линии действия: перпендикулярна к звену АВ, проводится на плане из точки а (конец вектора известна по линии действия: перпендикулярна к звену АВ, проводится на плане из точки а (конец вектора 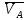 ). Скорость точки В относительно стойки направлена по линии хода ползуна, проводится на плане из полюса РV параллельно ходу ползуна до пересечения с вектором относительной скорости ). Скорость точки В относительно стойки направлена по линии хода ползуна, проводится на плане из полюса РV параллельно ходу ползуна до пересечения с вектором относительной скорости 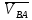 . Точка пересечения будет точкой b, определяющей конец вектора скорости . Точка пересечения будет точкой b, определяющей конец вектора скорости  : :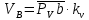 ; (2.6) ; (2.6) 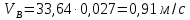 ; ; Вектор ab изображает скорость 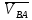 точки В в относительном вращении вокруг точки А: точки В в относительном вращении вокруг точки А: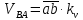 (2.7) (2.7)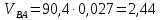 м/с м/сПоложение точки С находим на плане скоростей по свойству подобия (из пропорции): 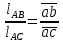 (2.8) (2.8)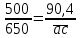 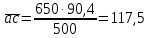 мм (2.9) мм (2.9)Откладываем от конца вектора 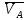 расстояние 117,5 мм вдоль вектора расстояние 117,5 мм вдоль вектора 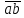 и получаем положение точки С. Соединив полученную точку с полюсом и получаем положение точки С. Соединив полученную точку с полюсом 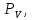 определим скорость точки С: определим скорость точки С: 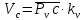 (2.10) (2.10)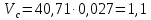 м/с м/сДля определения скорости точки D воспользуемся векторными равенствами: 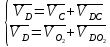 (2.11) (2.11)где 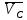 – скорость точки С, известна по значению и направлению; – скорость точки С, известна по значению и направлению;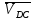 – относительная скорость точки D во вращении вокруг точки С; – относительная скорость точки D во вращении вокруг точки С;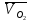 – скорость точки О2 (равна нулю); – скорость точки О2 (равна нулю);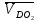 – относительная скорость точки D во вращении вокруг точки О2. – относительная скорость точки D во вращении вокруг точки О2.Относительные скорости 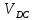 и и 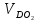 известны по линии их действия: известны по линии их действия: 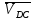 перпендикулярна к звену DC, проводится на плане из точки С (конец вектора перпендикулярна к звену DC, проводится на плане из точки С (конец вектора 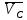 ); ); 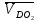 перпендикулярна к звену DO2, проводится на плане из точки О2 (в полюсе pV). На пересечении этих двух линий действия получаем точку D. Конец вектора скорости точки D перпендикулярна к звену DO2, проводится на плане из точки О2 (в полюсе pV). На пересечении этих двух линий действия получаем точку D. Конец вектора скорости точки D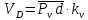 (2.12) (2.12)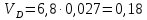 м/с м/сВектор dc изображает скорость vDC точки D в относительном вращении вокруг точки С: 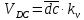 (2.13) (2.13)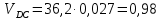 м/с (2.14) м/с (2.14)Исходя из теоремы подобия (третье свойство плана скоростей), находим на плане точки S1 – S5, соответствующие центрам тяжести звеньев. Соединив их с полюсом рV, определяем скорости центров тяжести звеньев механизма, м/с: 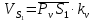 ; (2.15) ; (2.15)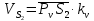 ; (2.16) ; (2.16)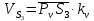 ; (2.17) ; (2.17)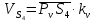 ; (2.18) ; (2.18)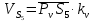 ; (2.19) ; (2.19)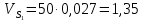 м/с м/с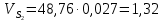 м/с м/с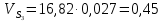 м/с м/с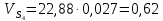 м/с м/с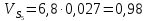 м/с м/сПользуясь планом скоростей, определяем угловые скорости звеньев 2, 4, 5, с-1: 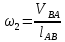 ; (2.20) ; (2.20)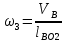 ; (2.21) ; (2.21)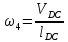 ; (2.22) ; (2.22)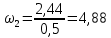 с-1 с-1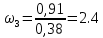 с-1 с-1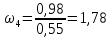 с-1 с-1Угловая скорость ползуна 5 = 0, так как он движется поступательно по неподвижной направляющей. Для выяснения направления угловой скорости звена АВ вектор скорости 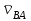 , направленной к точке b плана, мысленно переносим в точку В звена 2 и определяем, что он стремится повернуть это звено вокруг точки А по часовой стрелки. По аналогии определяем направления угловых скоростей звеньев 3 (по часовой стрелки) и 4 (против часовой стрелки). , направленной к точке b плана, мысленно переносим в точку В звена 2 и определяем, что он стремится повернуть это звено вокруг точки А по часовой стрелки. По аналогии определяем направления угловых скоростей звеньев 3 (по часовой стрелки) и 4 (против часовой стрелки). |
