Курсовая. Анализ и синтез плоских рычажных механизмов
 Скачать 179.01 Kb. Скачать 179.01 Kb.
|
2.5 Определение ускорений точек механизма методом планов ускоренийСчитая известным ускорение шарнирной точки ( 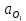 = = 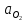 = 0), помещаем ее на плане ускорений в полюсе = 0), помещаем ее на плане ускорений в полюсе 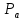 . Звено . Звено 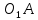 вращается равномерно, поэтому точка А имеет только нормальное ускорение, которое направлено по звену вращается равномерно, поэтому точка А имеет только нормальное ускорение, которое направлено по звену 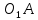 к центру вращения к центру вращения 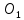 . Определяем его по формуле, м/ . Определяем его по формуле, м/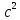 : : 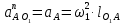 ; (2.23) ; (2.23)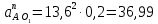 м/с2 м/с2Принимаем (произвольно) длину отрезка 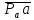 равной 100 мм. Тогда масштаб плана ускорений, (м/с2)/мм-1: равной 100 мм. Тогда масштаб плана ускорений, (м/с2)/мм-1: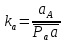 ; (2.24) ; (2.24)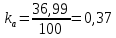 Из полюса плана ра откладываем 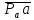 параллельно звену О1А в направлении от А к О1. параллельно звену О1А в направлении от А к О1.Рассматривая движения точки В со звеном АВ, составляем векторное уравнение: 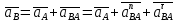 . (2.25) . (2.25)В этом уравнении ускорение точки А известно по величине и по направлению. Определяем нормальное ускорение точки В относительно А: 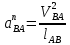 ; (2.26) ; (2.26)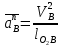 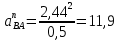 м/с2 м/с2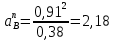 м/с2 м/с2На плане ускорений 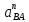 можно выразить отрезком можно выразить отрезком 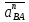 : :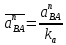 ; (2.27) ; (2.27)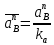 ; ;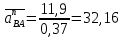 мм мм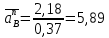 мм ммПроведем линии действия тангенциальных составляющих перпендикулярно нормальным составляющим. На пересечении этих перпендикуляров получим точку b. Соединив точки a и b получим ускорение звена AB, а соединив точку полюса с точкой b, получим ускорение самой точки B. Определяем ускорения точки В и звена AB, м/с2: 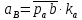 ; (2.28) ; (2.28) 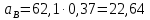 м/с2 м/с2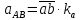 ; (2,29) ; (2,29)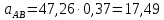 м/с2 м/с2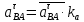 ; (2.30) ; (2.30)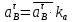 ; ; 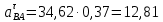 м/с2 м/с2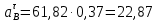 м/с2 м/с2Положение точки С на плане ускорений находим по свойству подобия (из пропорции): 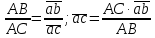 (2.30) (2.30)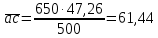 мм ммСоединив ее с полюсом, определяем ускорение точки С, м/с2: 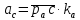 ; (2.31) ; (2.31)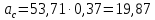 м/с2 м/с2Для дальнейшего построения плана ускорений и определения ускорения точки D составляем уравнение: 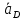 = = 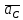 + + 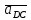 = = 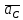 + + 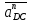 + + 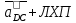 ; (2.32) ; (2.32)Определяем ускорения звена CD, м/ 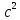 : :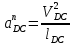 ; (2.33) ; (2.33)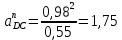 м/с2 м/с2От точки С плана ускорений параллельно звену DC в направлении от точки С к точке D откладываем вектор, изображающий ускорение 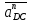 , длина которого: , длина которого: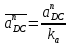 ; (2.34) ; (2.34)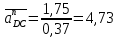 мм ммИз нормальных ускорения звена DC и ЛХП проведем перпендикуляры, пересечение которых даст точку d. Далее проводим ускорения 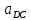 и и 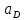 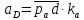 ; (2.35) ; (2.35)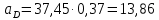 м/с2 м/с2Определяем тангенциальные ускорения и относительные во вращении вокруг точек С и D, м/с2: 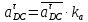 ; (2.36) ; (2.36)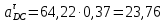 м/с2 м/с2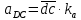 ; (2.37) ; (2.37)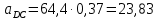 м/с2 м/с2Из третьего свойства планов ускорений (свойства подобия) определяем места положений точек центров тяжести, а затем величины ускорений: 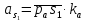 ; (2.38) ; (2.38)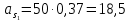 м/с2 м/с2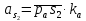 ; (2.39) ; (2.39) м/с2 м/с2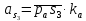 ; (2.40) ; (2.40)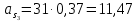 м/с2 м/с2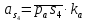 ; (2.41) ; (2.41)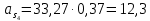 м/с2 м/с2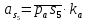 ; (2.42) ; (2.42)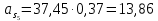 м/с2 м/с2Определяем угловые ускорения звеньев. Угловое ускорение 1 ведущего звена О1А, совершающего равномерное движение, равно нулю. Угловое ускорение звена 2: 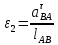 ; (2.43) ; (2.43)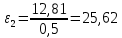 c-2 c-2Для определения направления углового ускорения 2 звена 2 надо мысленно перенести вектор тангенциального ускорения 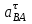 в точку В. В направлении этого вектора точка В вращается относительно точки А против часовой стрелки в точку В. В направлении этого вектора точка В вращается относительно точки А против часовой стрелки По аналогии определяем значения и направления угловых ускорений звеньев 3 и 4, с-2: 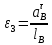 ; (2.44) ; (2.44)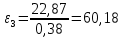 c-2 (по часовой стрелке) c-2 (по часовой стрелке)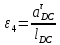 ; (2.45) ; (2.45)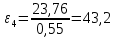 c-2 (против часовой стрелки) c-2 (против часовой стрелки) |
