Курсовая работа по информатике.. Аппроксимация функции методом наименьших квадратов
 Скачать 229.38 Kb. Скачать 229.38 Kb.
|
Расчёт с помощью таблиц, выполненных средствами Microsoft Excel.Для проведения расчётов данные целесообразно расположить в виде таблицы 2, используя средства табличного процессора Microsoft Excel.
Таблица 2. Пояснение к таблице 2. Шаг 1.В ячейки А1:A25 заносим значения xi. Шаг 2.В ячейки B1:B25 заносим значения уi. Шаг 3.В ячейку С1 вводим формулу=А1^2. Шаг 4.В ячейки С1:С25 эта формула копируется. Шаг 5.В ячейку D1 вводим формулу=А1*B1. Шаг 6.В ячейки D1:D25 эта формула копируется. Шаг 7.В ячейку F1 вводим формулу=А1^4. Шаг 8.В ячейки F1:F25 эта формула копируется. Шаг 9.В ячейку G1 вводим формулу=А1^2*B1. Шаг 10.В ячейки G1:G25 эта формула копируется. Шаг 11.В ячейку H1 вводим формулу=LN(B1). Шаг 12.В ячейки H1:H25 эта формула копируется. Шаг 13.В ячейку I1 вводим формулу=А1*LN(B1). Шаг 14.В ячейки I1:I25 эта формула копируется. Последующие шаги делаем с помощью авто суммирования . Шаг 15. В ячейку А26 вводим формулу=СУММ(А1:А25). Шаг 16. В ячейку В26 вводим формулу=СУММ(В1:В25). Шаг 17. В ячейку С26 вводим формулу=СУММ(С1:С25). Шаг 18. В ячейку D26 вводим формулу=СУММ(D1:D25). Шаг 19. В ячейку E26 вводим формулу=СУММ(E1:E25). Шаг 20. В ячейку F26 вводим формулу=СУММ(F1:F25). Шаг 21. В ячейку G26 вводим формулу=СУММ(G1:G25). Шаг 22. В ячейку H26 вводим формулу=СУММ(H1:H25). Шаг 23. В ячейку I26 вводим формулу =СУММ(I1:I25). Аппроксимируем функцию 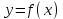 линейной функцией линейной функцией 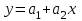 . Для определения коэффициентов . Для определения коэффициентов 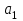 и и 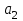 воспользуемся системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде воспользуемся системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде 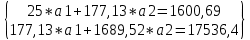 (11) (11)решив которую, получим a1 = -36,9917 и a2 = 14,2578 Систему решали методом Крамера. Суть которого состоит в следующем. Рассмотрим систему n алгебраических линейных уравнений с n неизвестными:  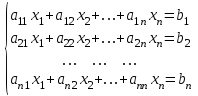 (12) (12)Определителем системы называется определитель матрицы системы: 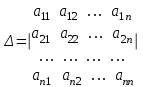 (13) (13)Обозначим 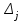 - определитель, который получится из определителя системы Δ заменой j-го столбца на столбец - определитель, который получится из определителя системы Δ заменой j-го столбца на столбец 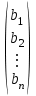 (14) (14)Таким образом, линейная аппроксимация имеет вид y = 14,258x-36,992 (15) Решение системы (11) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 3. Таблица 3.
В таблице 3 в ячейках A32:B33 записана формула {=МОБР(А28:В29)}. В ячейках Е32:Е33 записана формула {=МУМНОЖ(А32:В33),(C28:С29)}. Далее аппроксимируем функцию 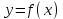 квадратичной функцией квадратичной функцией 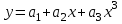 . Для определения коэффициентов a1, a2 и a3 воспользуемся системой (5). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 , D26, E26, F26, G26 запишем систему (5) в виде . Для определения коэффициентов a1, a2 и a3 воспользуемся системой (5). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 , D26, E26, F26, G26 запишем систему (5) в виде 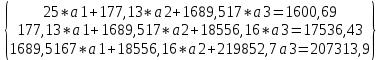 (16) (16)решив которую, получим a1 = -1,39325, a2 = 0,70294 и a3 = 0,894344 Таким образом, квадратичная аппроксимация имеет вид y =0,8943x^2+0,7029x-1,3933 (17) Решение системы (16) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 4. Таблица 4.
В таблице 4 в ячейках А41:С43 записана формула {=МОБР(А35:С37)}. В ячейках F41:F43 записана формула {=МУМНОЖ(А41:C43),(D36:D38)}. Теперь аппроксимируем функцию 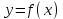 экспоненциальной функцией экспоненциальной функцией 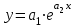 . Для определения коэффициентов . Для определения коэффициентов 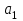 и и 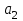 прологарифмируем значения прологарифмируем значения 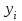 и, используя итоговые суммы таблицы 2, расположенные в ячейках A26, C26, H26 и I26, получим систему и, используя итоговые суммы таблицы 2, расположенные в ячейках A26, C26, H26 и I26, получим систему 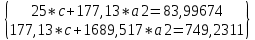 (18) (18)где 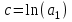 . .Решив систему (18), получим c = 0,847159 и a2 = 0,354642. После потенцирования получим a1 = 2,33301. Таким образом, экспоненциальная аппроксимация имеет вид y = 2,333e0,3546x (19) Решение системы (18) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 5. Таблица 5.
В таблице 5 в ячейках А50:A51 записана формула {=МОБР(А46:B47)}. В ячейках Е49:Е50 записана формула {=МУМНОЖ(A50:B51;C46:C47)} В ячейке Е51 записана формула=EXP(E49). Вычислим среднее арифметическое 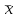 и и 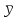 по формулам: по формулам: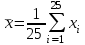 ; ; 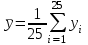 . .Результаты расчета 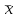 и и 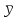 средствами Microsoft Excel представлены в таблице 6. средствами Microsoft Excel представлены в таблице 6.Таблица 6.
В ячейке В54 записана формула=А26/25. В ячейке В55 записана формула=В26/25 Для того, чтобы рассчитать коэффициент корреляции и коэффициент детерминированности данные целесообразно расположить в виде таблицы 7, которая является продолжением таблицы 2.
Таблица 7. Пояснение к таблице 7. Ячейки А1:А26 и В1:В26 уже заполнены . Далее делаем следующие шаги. Шаг 1.В ячейку J1 вводим формулу=(A1-$B$54)*(B1-$B$55). Шаг 2.В ячейки J2:J25 эта формула копируется. Шаг 3.В ячейку K1 вводим формулу=(A1-$B$54)^2. Шаг 4.В ячейки k2:K25 эта формула копируется. Шаг 5.В ячейку L1 вводим формулу=(B1-$B$55)^2. Шаг 6.В ячейки L2:L25 эта формула копируется. Шаг 7.В ячейку M1 вводим формулу=($F$32+$F$33*A1-B1)^2. Шаг 8.В ячейки M2:M25 эта формула копируется. Шаг 9.В ячейку N1 вводим формулу=($F$41+$F$42*A1+$F$43*A1^2-B1)^2. Шаг 10.В ячейки N2:N25 эта формула копируется. Шаг 11.В ячейку O1 вводим формулу=($F$51*EXP($F$50*A1)-B1)^2. Шаг 12.В ячейки O2:O25 эта формула копируется. Последующие шаги делаем с помощью авто суммирования . Шаг 13.В ячейку J26 вводим формулу =CУММ(J1:J25). Шаг 14.В ячейку K26 вводим формулу =CУММ(K1:K25). Шаг 15.В ячейку L26 вводим формулу =CУММ(L1:L25). Шаг 16.В ячейку M26 вводим формулу =CУММ(M1:M25). Шаг 17.В ячейку N26 вводим формулу =CУММ(N1:N25). Шаг 18.В ячейку O26 вводим формулу =CУММ(O1:O25). Теперь проведем расчеты коэффициента корреляции по формуле (8) (только для линейной аппроксимации) и коэффициента детерминированности по формуле (10). Результаты расчетов средствами Microsoft Excel представлены в таблице 8.
Таблица 8. В ячейке B57 записана формула=J26/(K26*L26) ^ (1/2). В ячейке B58 записана формула=1-M26/L26. В ячейке B59 записана формула=1-N26/L26. В ячейке B60 записана формула=1-O26/L26. Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
