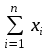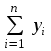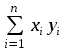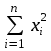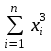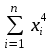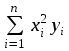капуф. Аппроксимация функций

• Название: Аппроксимация функций
• Анкор: капуф
• Дата: 28.05.2022
• Размер: 1.05 Mb.
• Имя файла: praktika (2).docx
• Тип: Документы; #554382

АППРОКСИМАЦИЯ ФУНКЦИЙ

1. 
   Нахождение параметров линейной функции
   

Предположим, что зависимость между x и y линейная, т.е. приближающую функцию можно записать в виде y=ax+b.

Нужно найти такие значения a и b, для которых функция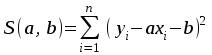

(2)

минимальна.

Условия функции (2) запишутся так: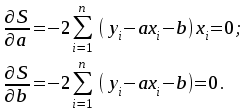



Преобразуя, получим для нахождения неизвестных (a и b) систему двух уравнений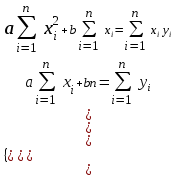

.

Суммы 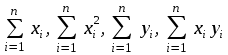вычисляются по табличным данным. Для удобства вычисления можно составить расчетную таблицу:

N	x	Y	xy	x2
1	x1	y1	x1y1	x12
2 … n	x2 ... xn	y2 … yn	x2y2 … xnyn	x22 … xn2
Σ

2. 
   Нахождение параметров квадратичной функции
   

Если известно, что приближающей функцией является квадратичная функция y=ax²+bx+c, то ее коэффициенты a, b, c найдем из условия минимума функции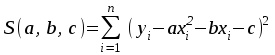

.

Условия минимума: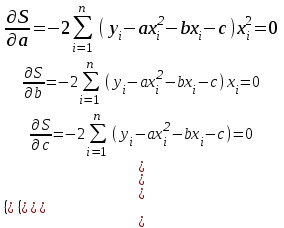



Получаем для нахождения неизвестных a, b, c систему трех уравнений, которую решаем методом Гаусса.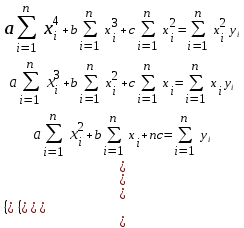



Расчетная таблица

N	x	y	x2	x3	x4	x2y	xy
1	x1	y1	x12	x13	x14	x12y1	x1y1
2 … n	x2 ... xn	y2 … yn	x22 … xn2	x23 … xn3	x24 … xn4	x22y2 … xn2yn	x2y2 … xnyn
Σ

Далее поступаем аналогично для всех уравнений регрессии, заполняем системы и находим коэффициенты aиb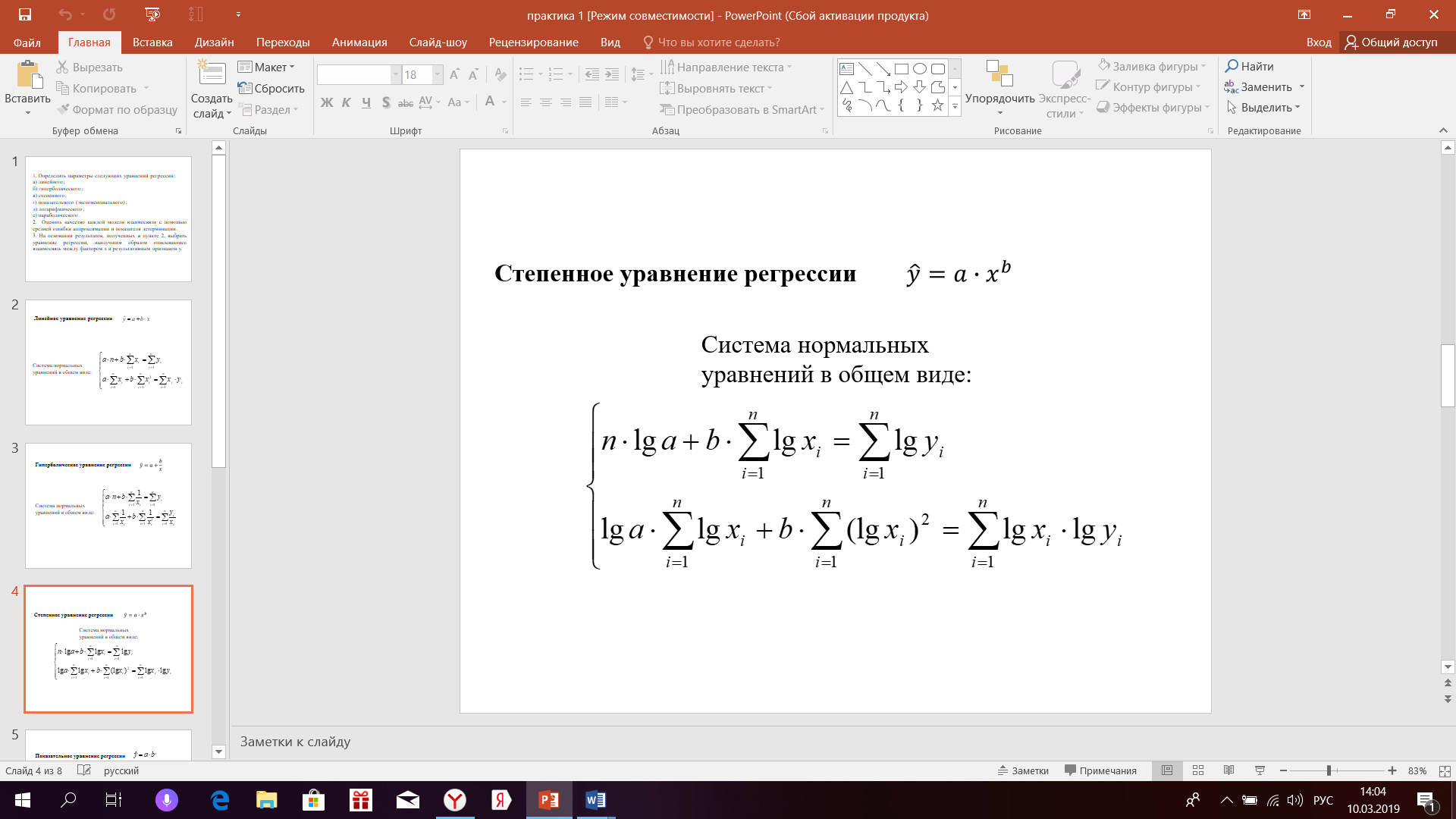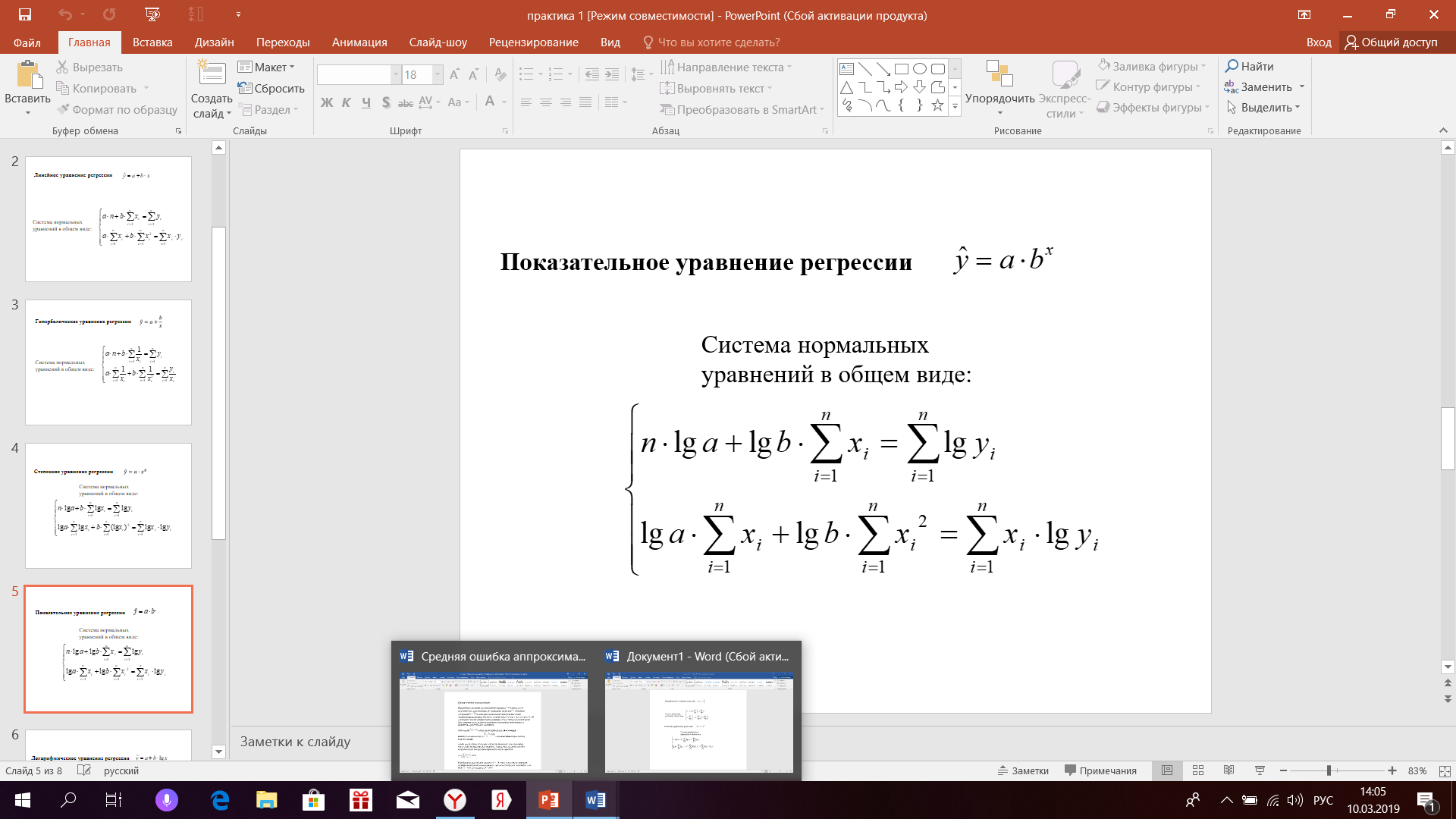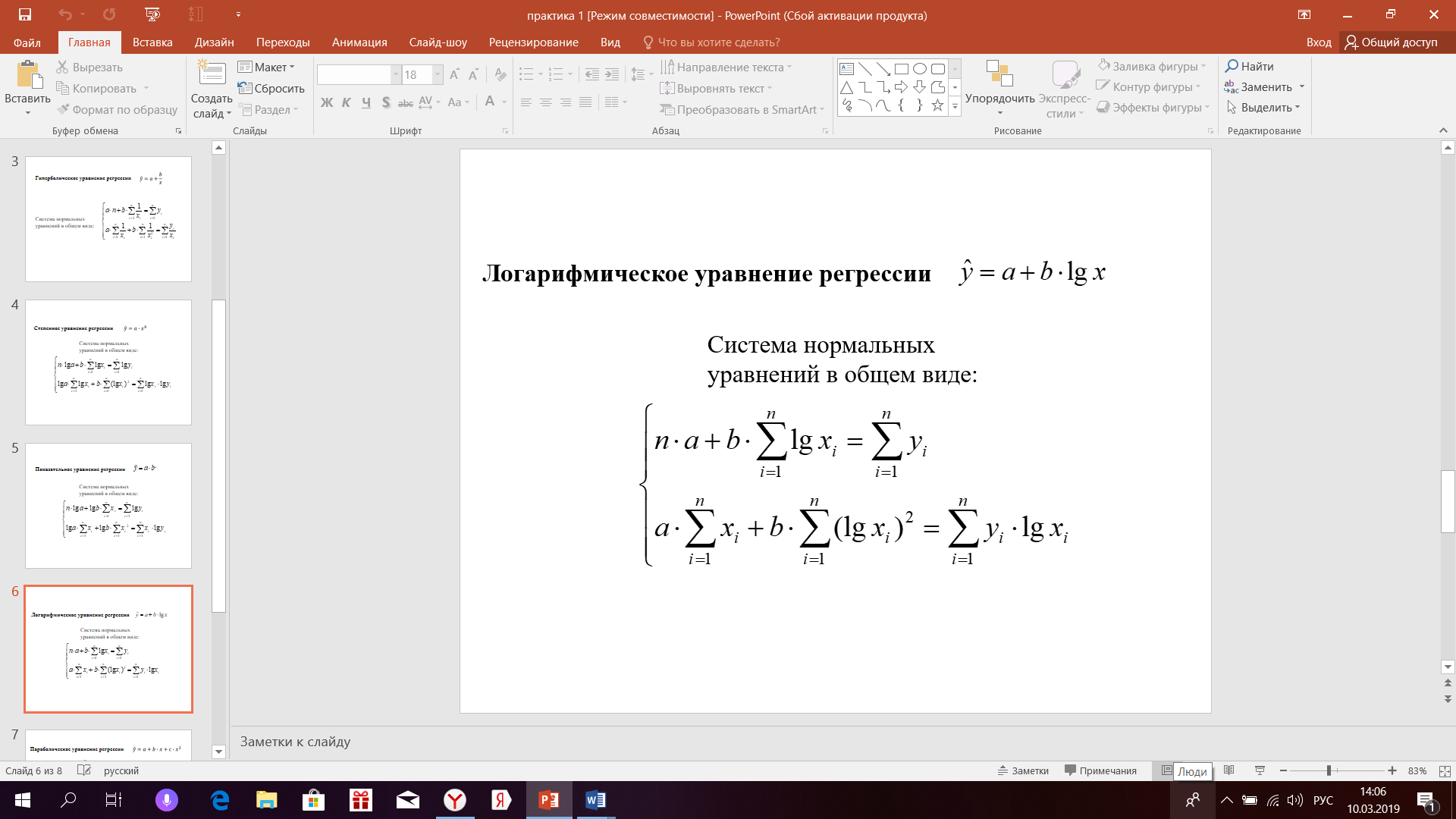











Оценка качества построенных уравнений регрессии

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических: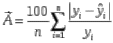



Допустимый предел значений 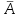- не более 8 – 10%

y_i - i-й элемент выборки; n - объём 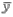выборки;

- среднее арифметическое выборки:

Показатель детерминации:



Задание:

1. Определить параметры следующих уравнений регрессии:

а) линейного;

б) гиперболического;

в) степенного;

г) показательного (экспоненциального);

д) логарифмического;

е) параболического.

2. Оценить качество каждой модели взаимосвязи с помощью средней ошибки аппроксимации и показателя детерминации.

3. На основании результатов, полученных в пункте 2, выбрать уравнение регрессии, наилучшим образом описывающее взаимосвязь между фактором х и результативным признаком у.