шпаргалки для 9 класса к огэ. шпаргалки для 9 класса. Арифметической прогрессией
 Скачать 2.25 Mb. Скачать 2.25 Mb.
|
|
Последовательность, в которой каждый следующий член можно найти, прибавив к предыдущему одно и то же число d, называется арифметической прогрессией. Последовательность (bn), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q, называется геометрической прогрессией.  Угол с вершиной в центре окружности называется центральным углом. 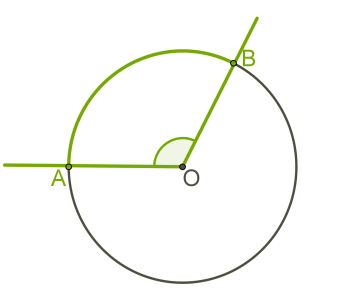 Градусная мера центрального угла равна градусной мере соответствующей дуги окружности: ∡ AOB= ∪AB. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.  Вписанный угол измеряется половиной дуги, на которую он опирается: ∡ACB=12∪AB. 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны. 2. Вписанный угол, опирающийся на полуокружность, равен 90°. 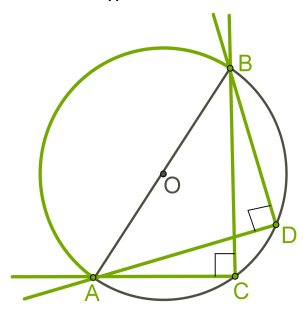 Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков второй хорды. Это свойство легко доказать, дополнив рисунок и рассмотрев подобие ΔCKA∼ΔBKD. Треугольники подобны, потому что имеют равные углы: ∡1 — вписанные углы, которые опираются на одну и ту же дугу, ∡2 — вертикальные углы. Если AKKD=CKKB, то AK⋅KB=CK⋅KD. 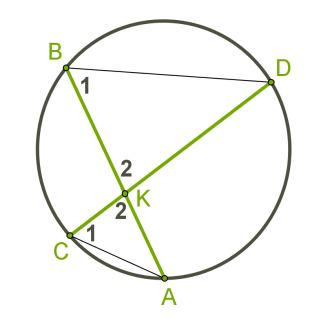 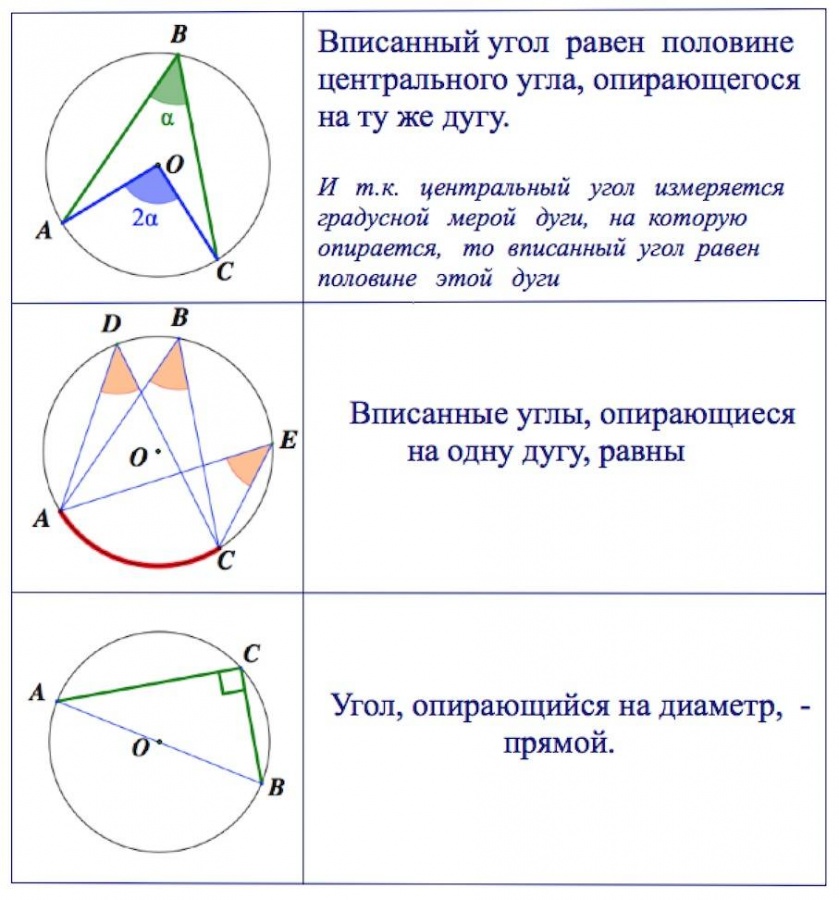 Решение линейных и квадратных неравенств Квадратным неравенством с одной переменной х называют неравенством вида ax2 +bx+c>0, где a,b,c – действительные числа (кроме а=0). При решение неравенств используют следующие правила: 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, при этом знак неравенства не меняется. 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства. 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный. Утверждения: 1. Если квадратный трехчлен ax2 +bx+c не имеет корней (т.е. его дискриминант D - отрицательное число) и если при этом a>0, то при всех значениях х выполняется неравенство ax2 +bx+c>0. 2. Если квадратный трехчлен ax2 +bx+c не имеет корней (т.е. его дискриминант D - отрицательное число) и если при этом a<0, то при всех значениях х выполняется неравенство ax2 +bx+c<0. Иначе говоря, если D<0, a<0 , то неравенство ax2 +bx+c<0 выполняется при всех х; напротив, неравенство ax2 +bx+c> 0 в этом случае не имеет решений. Теорема: Если квадратный трехчлен ax 2 +bx+c имеет отрицательный дискриминант, то при любом х значение трехчлена имеет знак старшего коэффициента а.      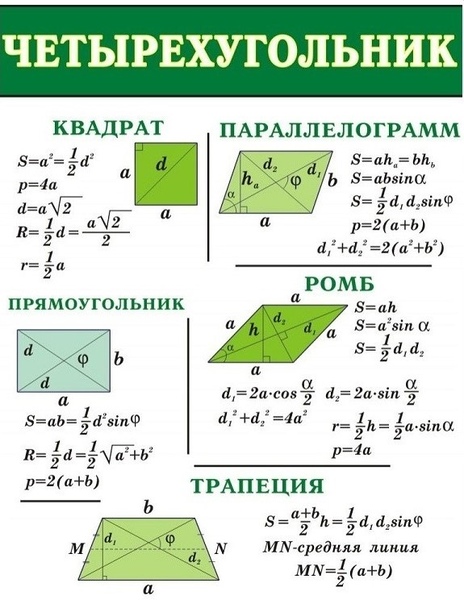 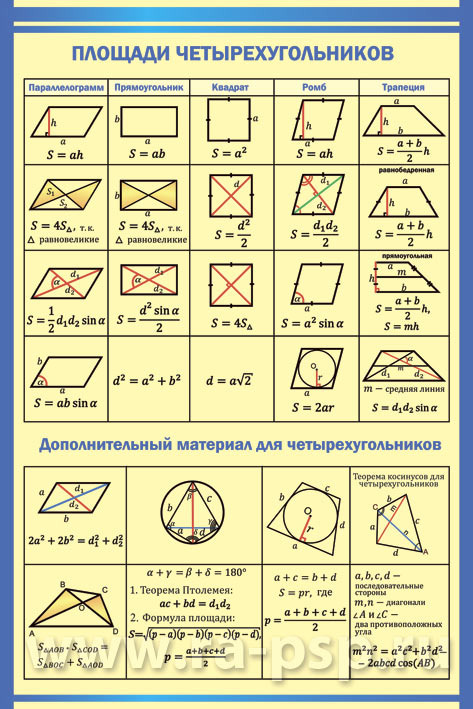 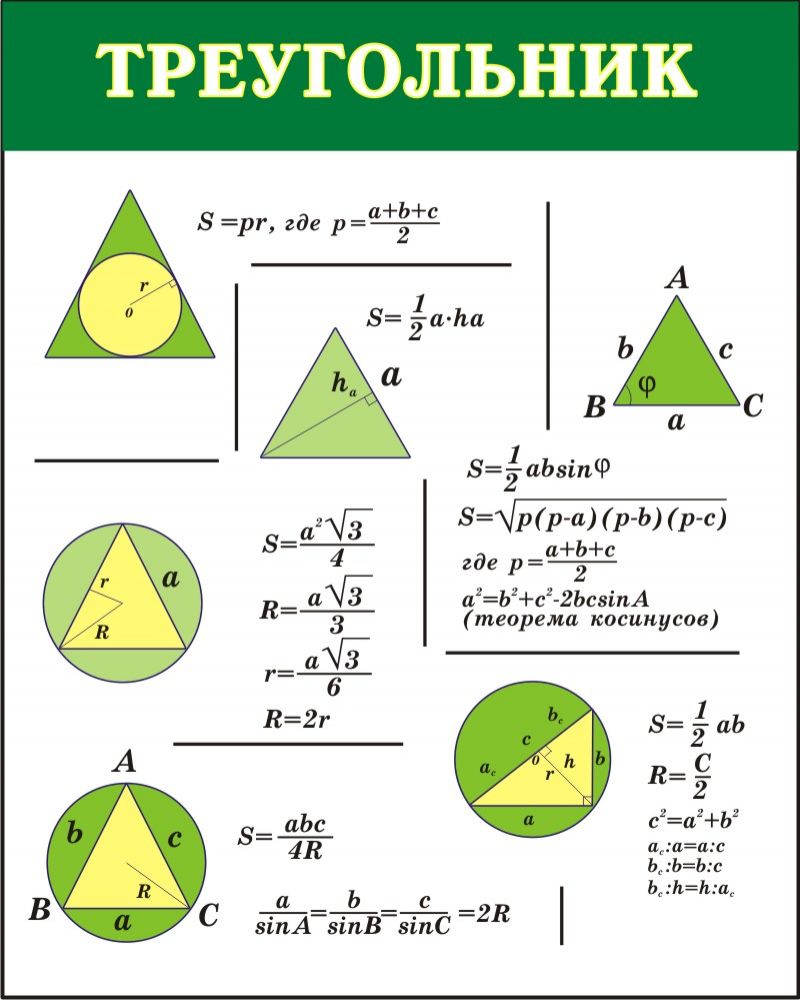 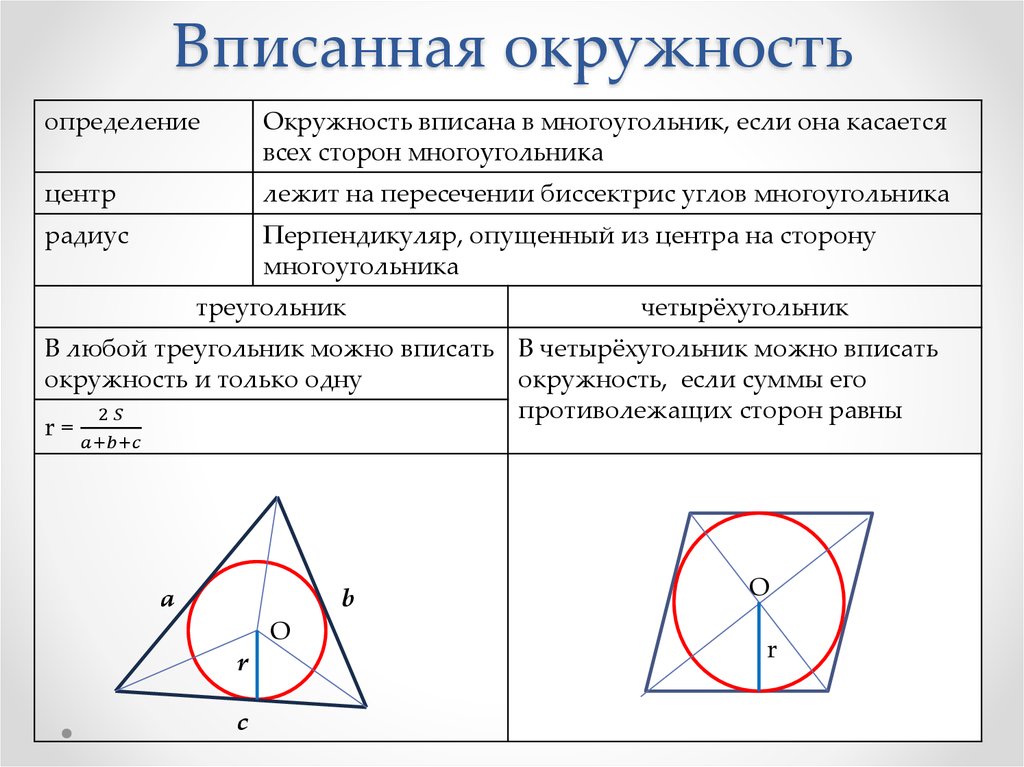  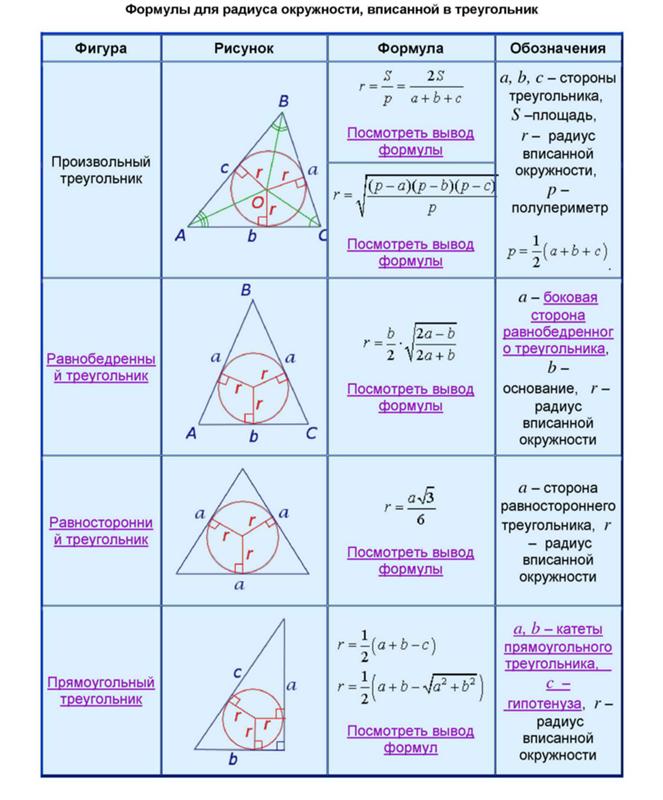   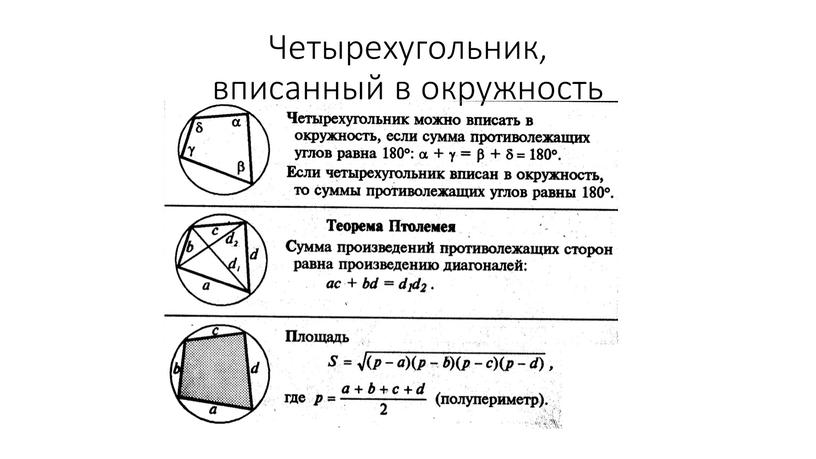 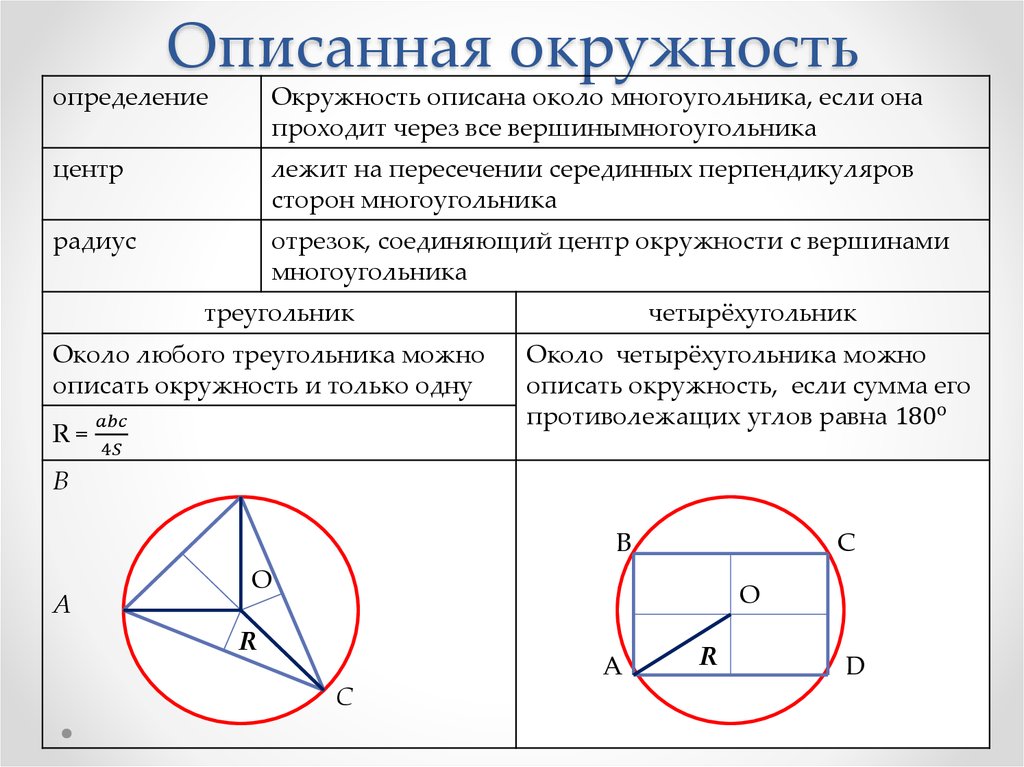  |
