Диссертация Повышение безопасной эксплуатации башенных кранов. диссертация. Асанхан Жаннур Оразханлы повышение безопасности эксплуатации стреловых кранов за счет снижения динамических нагрузок при подъёме груза магистерская диссертация
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
1.2 Характеристика возможных режимов и способов ведения работ на кранах Грузоподъемные машины являются машинами прерывного действия, у которых периоды работы перемежаются с периодами пауз, а механизмы работают разновременно или частично совмещенно. Цикл рабочего процесса характеризуются следующими операциями: захват груза и его подъем, передвижение крана, изменение вылета, вращение поворотной части крана, опускание груза и его отцепка – возврат крюка в его исходное положение. Как показывают исследования, наиболее неблагоприятными режимами работы крановых механизмов подъёма являются режимы подъёма груза, лежащего на полу, и стопорного торможения груза, опускающегося с номинальной скоростью или скоростью, существенно превышающей номинальную. В период разгона и торможения помимо статических нагрузок должны быть приложены дополнительные усилия для преодоления сил инерции вращающихся частей лебёдки и подвешенного груза. Так как грузовой канат и несущие конструкции крана не являются абсолютно жёсткими, приложение усилий приводит к колебаниям [6]. Малые веса конструкций, большие высоты и скорости подъёма, характерные для башенных кранов, являются причинами того, что на практике колебательный характер разгона и торможения явно ощутим. Это приводит к значительному возрастанию динамических нагрузок и в ряде случаев является причиной поломок и аварий [6]. В процессе работы башенного крана часто возникает вероятность его перегрузки из–за человеческого или технологического факторов. Перегрузка кранов – одна из основных причин аварий, поэтому нельзя эксплуатировать краны с отключенным или неисправным ограничителем грузоподъемности (на кранах, снабженных такими приборами), поднимать груз неизвестной массы, засыпанный землей, заложенный другими грузами, укрепленный болтами или залитый бетоном, а также металл и шлак, застывший в печи или приварившийся после слива. Недопустимо с помощью грузоподъемной машины производить освобождение защемленных грузом стропов. Такая операция может привести к перегрузке машины или обрыву стропов. Наиболее тяжелые аварии в результате перегрузки происходят с башенными и стреловыми самоходными кранами. Перегрузка таких кранов может вызвать их падение (опрокидывание) или обрыв стреловых канатов и падение стрелы. Для обеспечения надежной и безопасной работы кран должен обладать устойчивостью против опрокидывания, т.е. способностью противодействовать опрокидывающим кран нагрузкам. Обязательным условием сохранения устойчивости крана является превышение или равенство удерживающего момента сумме опрокидывающих. Колебания груза, приведенные к оголовку стрелы, возникающие при резком подъеме груза, порождают резонансные явления, являющиеся источником резкого повышения амплитуды колебаний и увеличения динамической составляющей нагрузки выше допустимой. В результате возникающий колебательный процесс в системе полиспаста приводит к потере устойчивости крана и дальнейшему его аварийному опрокидыванию. Важным критерием в обеспечении устойчивости крана являются погрешность срабатывания и быстродействие системы. От быстроты реагирования системы зависит ее безопасное осуществление технологического процесса, в особенности, такой параметр как скорость подъема и опускания груза имеет важное значение в определении показателей динамических нагрузок. Ввиду этого, данные скоростных значений кранов представлены в таблице 1.3. Таблица 1.3 Технические характеристики башенного крана
Скорость плавной посадки груза является наименьшей и для разных кранов находится в пределах 2–5 м/мин [7]. Затем с нарастающими показателями идут: скорость передвижения крана 12,5–40 м/мин; скорость подъема груза максимальной массы 6,3–70 м/мин; скорость передвижения грузовой тележки с максимальным грузом 20–50 м/мин. Исходя из представленных скоростных характеристик башенных кранов, можно сделать вывод, что при интенсивной изменчивости влияния динамической нагрузки на металлоконструкции крана, система не в состоянии оперативно на них отреагировать, так как при больших рабочих скоростях, нагрузки могут внезапно как возникнуть, так и сойти на нет. Наиболее опасные динамические нагрузки при работе механизма подъема возникают в начале подъема груза с подхватом, когда груз рывком отрывается от опоры. В момент отрыва груза весом Grp грузозахватное устройство имеет некоторую скорость установившегося движения. Нарастание нагрузки в канатах полиспаста происходит за весьма короткое время с большим ускорением, и значение нагрузки зависит от скорости подъема. При этом перегрузка крана может возникнуть при разных режимах работы: в период до отрыва груза от основания, после его отрыва или при резком обрыве груза, которые приводят к колебательным процессам в металлоконструкциях крана. Ввиду этого предлагается идея усовершенствования крюковой подвески крана, заключающаяся в том что, в конструкции подвески включается упругие и диссипативные элементы. Принцип работы предлагаемого изобретения заключается в том что, при нагружении крюковой подвески крана грузом, в случае резкого снятия нагрузки возникают резонансные частоты колебания всей конструкции крана, которые могут повлечь за собой аварийные ситуации. Ввиду этого в упругой крюковой подвеске крана предусмотрено применение демпфирующих и диссипативных элементов, которые позволят достичь затухания резонансных колебаний в точке их возникновения. Достижение такого результата обусловлено особенностью свойств демпфирующих и диссипативных элементов и конструкции крюковой подвески (рисунок 1.12). 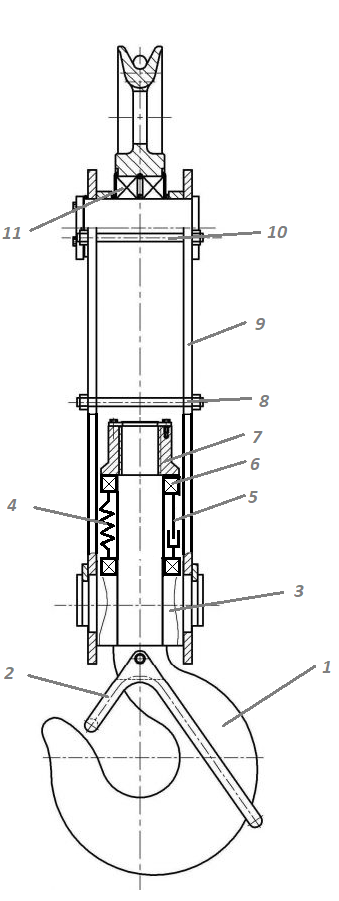 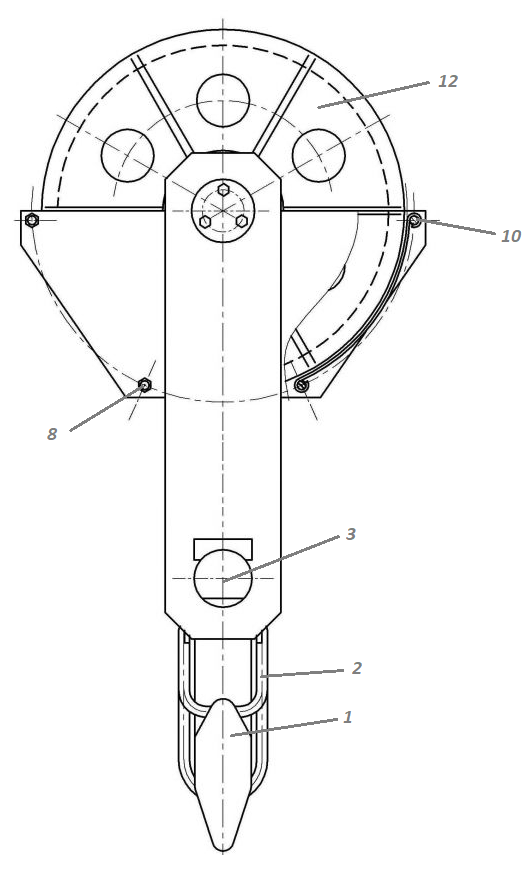 Рисунок 1.12 – Схема упругой крюковой подвески 1 – грузозахватный орган; 2 – предохранительный замок; 3 – траверса; 4 – упругий элемент; 5 – вязкий элемент; 6, 11 – шарикоподшипники; 7 – удерживающая гайка; 8, 10 – втулки; 9 – корпусные щеки; 12 – блок Результатом расположения двух элементов в определенном порядке и количестве является, равномерное распределение динамических усилий, возникающих при эффективном использовании упругой подвески. 2 Математическая модель механизма подъема башенного крана 2.1 Приведенные масса и жесткость Соотношение науки и практики всегда было главной философской проблемой всех исследователей. Вопрос о том, насколько верно те или иные рассуждения, расчеты, действия человека отражают суть реальности, является коренным вопросом любой научной теории [8]. Познанное человечеством по отношению к реальности можно условно иллюстрировать (рисунок 2.1). Реальность всегда бесконечнообразна и бесконечномерна, поэтому границы ее на рисунке обозначены пунктиром. То, что мы знаем, представляет собой лишь тонкий срез, отпечаток реальности, имеющий конечные размеры и свойства [8]. 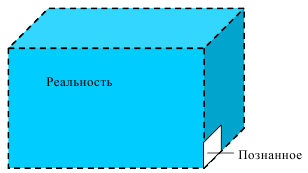 Рисунок 2.1 – Познанное человечеством по отношению к реальности весьма незначительно В силу ограниченности органов чувств и познаний человечеству дано лишь составлять себе то или иное представление о реальности. Для науки существенное значение имеет уверенная оценка близости такого ограниченного представления (субъективной реальности) к объективной реальности. Оценить эту близость практикой, полагая ее истиной, невозможно, так как мы можем исследовать лишь тот ограниченный круг свойств, который нам доступен. Если один человек что–то новое познал о реальности, он стремится объяснить это другим людям. И здесь возникает необходимость использовать терминологию, единообразно понимаемую собеседниками, которая неизбежно содержит какие–то упрощения – абстракции. Абстракции позволяют отсечь, отбросить из рассмотрения малозначительные факторы, ввести однозначные термины и представить себе объект в более простой форме, доступной формальной человеческой логике [8]. Таким образом, познанное одним человеком передается другому в усеченном виде – в виде некоторых моделей. Соотношение познанного и моделей можно иллюстрировать (рисунок. 2.2). На нем подчеркнута возможность существования для одного познанного явления нескольких моделей, отражающих те или иные его свойства в различных условиях. Для одного познанного явления могут существовать множество моделей, отражающих те или иные его свойства в различных условиях. Не существует единой модели, полностью отражающей все свойства познанного (объекта изучения). 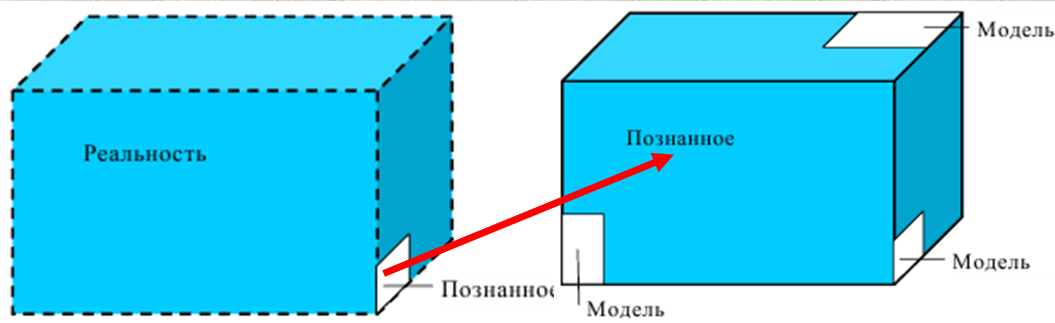 Рисунок 2.2 – Соотношение познанного и моделей В свою очередь различают два уровня научного познания: эмпирический и теоретический, неразрывно связанные друг с другом. Эмпирический уровень научного познания – это непосредственное исследование чувственно воспринимаемых объектов. В основе эмпирического познания лежит непосредственное практическое взаимодействие исследователя и изучаемого им объекта (наблюдение, эксперимент, измерение, описание). Теоретический уровень научного исследования – это раскрытие сущности явлений, выявление законов на рациональной (логической) ступени познания. На теоретическом уровне используются такие методы как анализ и синтез, абстрагирование и конкретизация, дедукция (цепь умозаключений (рассуждений), в результате которых их общих знаний человек получает знание конкретное) и индукция (умозаключение от фактов к общему утверждению), аналогия, историческое и логическое моделирование, математизация, а также такие исследовательские подходы, как системный, структурно–функциональный и другие. Но есть общенаучные методы, которые используются как на эмпирическом уровне, так и на теоретическом. Таким общенаучным методом является моделирование. Моделирование – метод познания окружающего мира путем построения и использования модели. При построении и исследовании модели могут применяться практически все остальные методы познания. Модель – материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект – оригинал, сохраняя некоторые важные для данного исследования типичные его черты [9]. Любая модель нетождественна объекту – оригиналу, поскольку при ее построении исследователь учитывал лишь важнейшие с его точки зрения факторы. В этом отношении любая модель является неполной [10]. «Полная» модель, очевидно, будет полностью тождественна оригиналу (Норберт Винер: «Наилучшей моделью кота является другой кот, а еще лучше – тот же самый кот»). Адекватность модели зависит от целей моделирования и принятых критериев. Идеально адекватная модель принципиально невозможна в силу неполноты модели [11]. Если результаты моделирования удовлетворяют исследователя и могут служить основой для прогнозирования поведения или свойств исследуемого объекта, то говорят, что модель адекватна объекту [12]. Как процесс, моделирование имеет основные стадии, представленные на рисунке 2.3. 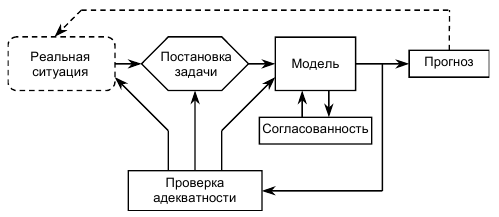 Рисунок 2.3 – Основные стадии моделирования Использование моделирования на эмпирическом и теоретическом уровнях исследования приводит к делению (условному) моделей на материальные и идеальные. Материальное (физическое) моделирование – это моделирование, при котором исследование объекта происходит с использованием его материального аналога воспроизводящего основные физические, геометрические, динамические и функциональные характеристики данного объекта [13]. Основными разновидностями материального (физического) моделирования является натурное и аналоговое. Натурное моделирование – это такое моделирование, при котором реальному объекту ставится в соответствие его увеличенный или уменьшенный материальный аналог, допускающий исследование с помощью последующего перенесения свойств изучаемых процессов и явлений с модели на объект на основе теории подобия [14]. Аналоговое моделирование – это моделирование, основанное на аналогии процессов и явлений, имеющих различную физическую природу, но одинаково описываемых формально (одними и теми же математическими соотношениями, логическими и структурными схемами) [14]. Идеальное моделирование разделяют на два основных типа: интуитивное и научное. Интуитивное моделирование – это моделирование, основанное на интуитивном (не обоснованном с позиций формальной логики) представлении об объекте исследования, не поддающимся формализации или не нуждающимся в ней. В качестве наиболее яркого примера интуитивной модели окружающего мира можно считать жизненный опыт любого человека. Любое эмпирическое знание без объяснения причин и механизмов наблюдаемого явления также следует считать интуитивным [14]. Научное моделирование – это всегда логически обоснованное моделирование, использующее минимальное число предположений, принятых в качестве гипотез на основании наблюдений за объектом моделирования [14]. Существует два уровня математического моделирования технических объектов: микроуровень и макроуровень [15]. На микроуровне технический объект представляется как сплошная среда, состоящая из множества элементов взаимодействующих между собой в трехмерном геометрическом пространстве в соответствии с фундаментальными законами физики (сохранения энергии, массы, импульса) [15]. На макроуровне осуществляют проектирование различных машин и механизмов. Объекты проектирования рассматриваются как сложные технические системы, состоящие из совокупности взаимодействующих элементов [15]. Таким образом, в отличие от микроуровня, где объектами проектирования были детали машин (валы, корпуса, панели и т.п.), на макроуровне объект имеет сложную неоднородную структуру, состоящую из элементов – объектов проектирования микроуровня. Моделирование рабочих процессов транспортной техники с целью ее совершенствования или создания новых машин и механизмов в основном осуществляется на макроуровне, когда объект транспортной техники представляется состоящим из совокупности взаимодействующих элементов (объектов проектирования микроуровня), которые в дальнейшем рассматриваются в виде неделимой единицы (дискретного элемента), имеющей вход и выход. Дискретный (отдельный) элемент в общем случае обладает инерционными, упругими и диссипативными свойствами. Различают простые и сложные элементы. Простой элемент наделен только одним из упомянутых физических свойств, а сложный – более чем одним [15]. Таким образом, объекты проектирования на макроуровне рассматриваются как системы, состоящие из совокупности взаимодействующих дискретных элементов. Задача проектирования таких объектов состоит в определении оптимальных параметров и структуры исходя из заданного описания внешней среды и технических требований к объекту. Математическая модель динамической системы с сосредоточенными параметрами – система обыкновенных дифференциальных уравнений. На макроуровне для выделения дискретных элементов из сплошной среды в основном используют методы: – функционально законченных элементов; – сосредоточенных масс. Метод функционально законченных элементов основан на выделении типовых элементов технического объекта, завершенных в конструктивном отношении и предназначенных для выполнения определенных функций (например, в гидромеханической системе – участок гидромагистрали, золотниковый клапан, дроссель, обратный клапан, насос, гидромотор и др.). Метод сосредоточенных масс применим к техническим объектам, у которых масса распределена в пространстве неравномерно. Этот метод предназначен для моделирования технических объектов, где мерой инертности элементов служит масса. При построении динамической модели методом сосредоточенных масс выделяют: – абстрактные (условные) элементы, массы которых эквивалентны (эквивалентны – значит имеют такую же энергию) массам соответствующих частей технического объекта и сосредоточены в точке; – и элементы, лишенные массы (невесомые), отображающие характер взаимодействия сосредоточенных масс (рычаги, нити, пружины, валы и т.д.) Сосредоточенные массы обладают инерционными свойствами и способностью накапливать кинетическую энергию. Взаимодействие сосредоточенных масс осуществляется посредством упругих, диссипативных, фрикционных и трансформаторных элементов [15]. Упругие элементы отображают упругие свойства динамической системы. Они обладают способностью накапливать потенциальную энергию [15]. Диссипативные элементы отображают свойства диссипации (рассеивания) энергии конструктивными элементами технического объекта, обусловленные силами внутреннего трения, пропорциональными относительной скорости перемещения взаимодействующих сосредоточенных масс [15]. Фрикционные элементы отображают физические свойства фрикционных механизмов технического объекта [15]. Трансформаторные элементы отображают безынерционные преобразования параметров потока энергии, осуществляемые техническими устройствами, называемыми трансформаторами. Положение сосредоточенных масс в многомерном фазовом пространстве (в каждый момент времени может быть указано только одно положение системы) характеризуется геометрическими координатами и скоростью – фазовые координаты типа потока. Взаимодействие сосредоточенных масс отображается переменными типа потенциала – сила, момент, давление, напряжение. Фазовые координаты типа потока выбирают в качестве обобщенных координат (минимальное число независимых координат, определяющих конфигурацию системы). Количество независимых обобщенных координат системы равно числу ее степеней свободы. В общем случае не все введенные фазовые переменные типа потока будут независимыми. Переменные же типа потенциала всегда принадлежат к зависимым и выражаются через переменные типа потока [15]. Ограничения на изменения геометрических координат и скоростей движения сосредоточенных масс динамической системы называют связями. Если в динамической модели выбрать только такие независимые координаты, которые отображают лишь допустимые перемещения сосредоточенных масс, то сложное движение твердого тела раскладывается на простейшие составляющие – поступательное и вращательное. Поступательное движение твердого тела характеризуется линейной скоростью v и силой F, а вращательное – угловой скоростью ω и вращающим моментом М. Они и принимаются в качестве фазовых переменных механической системы: – фазовые переменные типа потока – скорости v, м/с, ω, рад/с; – фазовые переменные типа потенциала – силы F, Н, вращающие моменты М, Н м. Параметры элементов. Параметром инерционного элемента при поступательном движении является масса m, кг, а при вращательном движении – момент инерции I, кг·м2. Параметр диссипативного элемента – коэффициент сопротивления μ, называемый также коэффициентом неупругого сопротивления, коэффициентом вязкого трения, коэффициентом демпфирования. При поступательном движении он измеряется в Н·с/м, а при вращательном – в Н·м·с/рад. Параметр упругого элемента – коэффициент жесткости с. При поступательном движении в качестве единицы измерения с используется Н/м, а при вращательном – Н·м/рад. Математическая модель в общем случае содержит компонентные и топологические уравнения. Компонентные уравнения описывают свойства элементов объекта. В них входят переменные типа потенциала и типа потока. Топологические уравнения отражают связи между фазовыми переменными объекта. В них входят переменные одного типа: либо потенциала, либо потока. Топологические уравнения могут выражать законы сохранения, условия непрерывности, равновесия, баланса и т. п. Компонентные уравнения механической системы. Компонентное уравнение инерционного элемента получают на основе второго закона Ньютона. Для поступательного движения твердого тела уравнение имеет вид: 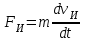 : (2.1) : (2.1)а для вращательного 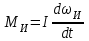 , (2.2) , (2.2)где FИ, МИ– соответственно сила инерции и момент сил инерции (или инерционный момент) элементов; vИ, ωИ– скорости инерционных элементов. Скорости vИ и ωИ представляют собой абсолютные скорости сосредоточенных масс соответственно при поступательном и вращательном движениях. Если твердое тело совершает сложное движение, то его раскладывают на простейшие составляющие, выделяют соответствующие им сосредоточенные массы и для каждой из них составляют свое компонентное уравнение инерционного элемента. Математическое описание диссипативного элемента основано на использовании закона Ньютона для вязкого трения: сила вязкого трения пропорциональна относительной скорости перемещения элементов трения. При поступательном движении компонентное уравнение имеет вид: 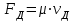 : (2.3) : (2.3)а при вращательном 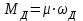 , (2.4) , (2.4)где FД, МД – соответственно сила и момент диссипативных элементов; vДи ωД – скорости диссипативных элементов. Математическое описание упругого элемента. Согласно закону Гука сила упругости деформируемого механического элемента при поступательном движении FУ или момент упругости МУ – при вращательном пропорциональны деформации: 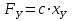 : (2.5) : (2.5)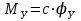 , (2.6) , (2.6)где хУ , φУ — соответственно линейная и угловая деформации. Упругие и диссипативные элементы в динамической модели соединяют между собой сосредоточенные массы. При движении системы под действием приложенных к ней внешних сил и моментов происходит изменение ее кинетической и потенциальной энергий, а часть энергии затрачивается на преодоление сил трения. Инерционные элементы динамической модели отображают свойство системы накапливать кинетическую энергию, упругие элементы – свойство накапливать потенциальную энергию, а диссипативные – рассеивать энергию на трение путем превращения механической энергии в тепловую. Как процесс, математическое моделирование имеет основные этапы. Этап 1. Обследование объекта моделирования. Основная цель – подготовка содержательной постановки задачи моделирования, т.е. формулирование в словесной (содержательной) форме основных вопросов об объекте моделирования, интересующих исследователя. Подготовка списка вопросов, на которые должна ответить модель требует не только хороших знаний в предметной области моделирования, но и знать объект моделирования, нюансы его поведения. Содержательная постановка задачи. Разработать математическую модель механизма подъема груза башенного крана, позволяющую исследовать его динамику с учетом характеристик взаимодействия элементов механизма как между собой, так и с металлоконструкцией крана. Модель должна позволять: – вычислять положение элементов башенного крана; – определять фазовые переменные типа потока и их производные. Исходные данные (результат обследования): – массы элементов механизма и металлоконструкции крана; – геометрические характеристики; – параметры связей между элементами механизма подъема и металлоконструкции крана. Этап 2. Концептуальная постановка задачи моделирования. Концептуальная постановка задачи моделирования – это сформулированный в терминах конкретных дисциплин (например, естественно – научных) перечень основных вопросов, интересующих исследователя, а также совокупность гипотез о поведении объекта, его взаимодействии с окружающей средой, изменении внутренних параметров. Согласно принятым гипотезам определяется множество параметров, описывающих состояние объекта, а также перечень законов, управляющих изменением и взаимосвязью этих параметров между собой (например, канат грузоподъемного крана). Как правило, эти гипотезы правдоподобны в том смысле, что для их обоснования могут быть приведены некоторые теоретические доводы и использованы экспериментальные данные, основанные на собранной ранее информации об объекте. Исследуемая система представляется состоящей из взаимосвязанных сосредоточенных масс, движение которых может быть описано в соответствии с законами классической механики. Принимаются следующие допущения: – взаимодействие сосредоточенных масс осуществляется посредством упругих элементов; – учитываются только массы башни, стрелы, груза и элементов привода; – характеристика двигателя считается абсолютно жесткой, т.е. крутящий момент не зависит от частоты вращения; – учитываются только вертикальные перемещения масс. Этап 3. Математическая постановка задачи моделирования. Определение перемещений, скоростей и ускорений сосредоточенных масс из решения системы дифференциальных уравнений. Движение сосредоточенных масс может быть описано в соответствии с законами классической механики. Приведение вращающихся масс привода (рисунок 2.4) осуществляется из условия равенства кинетической энергии приведенной массы сумме кинетических энергий масс, которые она заменяет. 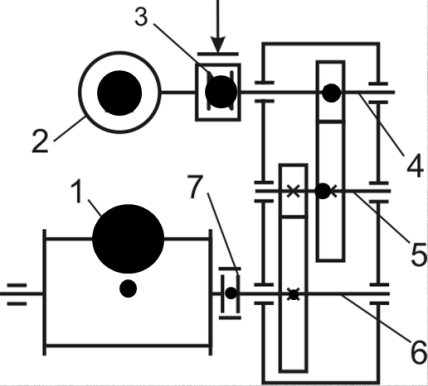 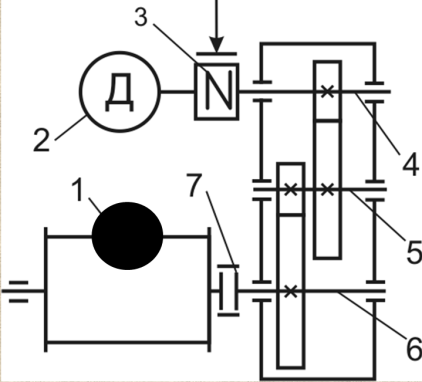 а) б) а) – до применения метода сосредоточенных масс б) – после применения метода сосредоточенных масс 1 – барабан; 2 – двигатель; 3 – быстроходная муфта; 4 – быстроходный вал; 5 – среднеходный вал; 6 – тихоходный вал; 7 – тихоходная муфта Рисунок 2.4 – Схема механизма подъема для определения массы, приведенной к барабану и совершающей вращательное движение Параметром инерционного элемента при вращательном движении является инерционный момент – I, кг·м2, который определяется по формуле 2.7. 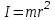 (2.7) (2.7)Приведенная к барабану масса привода, совершающая вращательное движение, определится из выражения (формула 2.8): 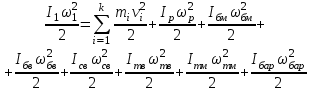 , (2.8) , (2.8)где 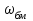 – угловая скорость быстроходной муфты, рад/с; – угловая скорость быстроходной муфты, рад/с;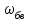 – угловая скорость быстроходного вала, рад/с; – угловая скорость быстроходного вала, рад/с;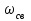 – угловая скорость среднеходного вала, рад/с; – угловая скорость среднеходного вала, рад/с;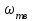 – угловая скорость тихоходного вала, рад/с; – угловая скорость тихоходного вала, рад/с; – угловая скорость тихоходного муфты, рад/с; – угловая скорость тихоходного муфты, рад/с;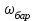 – угловая скорость барабана, рад/с. – угловая скорость барабана, рад/с.По принципу Даламбера: геометрическая сумма всех сил или моментов, приложенных к твердому телу, включая силу инерции, равна нулю, следственно выражение 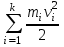 = 0. После преобразования формулы 2.14 получим конечное выражение (формула 2.9) = 0. После преобразования формулы 2.14 получим конечное выражение (формула 2.9)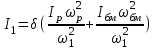 , (2.9) , (2.9)С учетом того, что 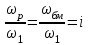 где i– передаточное число механизмов Приведенный в валу барабана момент инерции привода механизма подъема составит: 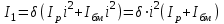 (2.10) Приведение массы металлоконструкции крана к оголовку стрелы крана (рисунок 2.5). 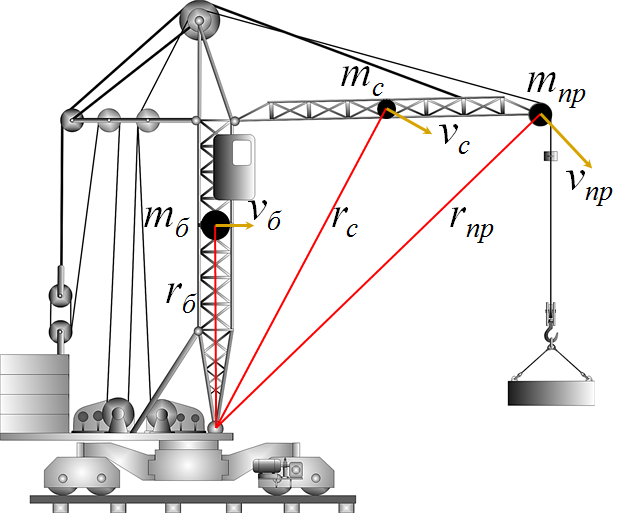 mб – масса башни, mс – масса стрелы, mпр – приведенная масса Рисунок 2.5 – Схема приведения масс металлоконструкции крана Приведение массы башни и стрелы к оголовку стрелы осуществляется из условия равенства кинетической энергии приведенной массы сумме кинетических энергий масс, которые она заменяет (формула 2.11). 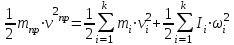 (2.11) (2.11)Отсюда следует что, выражение 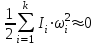 где mпр –приведенная масса; vпр, ωпр– приведенная линейная и угловая скорости звена приведения; mi, Ii– масса и момент инерции i–го звена механизма; vi, ωi– линейная и угловая скорости i–го звена механизма. После алгебраических преобразований приведенная к оголовку стрелы масса определится из выражения (формула 2.12):  (2.12) (2.12)С учетом того, что: 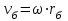 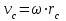 (2.13) (2.13)Тогда формула определения приведенной массы выглядит следующим образом; 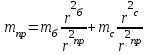 (2.14) (2.14)В соответствии с расчетной схемой математическая модель механизма подъема груза будет содержать компонентные уравнения инерционного элемента и упругого элемента. Взаимосвязь между однотипными переменными будет установлена на основе первого топологического уравнения – уравнения равновесия (принцип Д’Аламбера): геометрическая сумма всех сил или моментов, приложенных к твердому телу, включая силу инерции, равна нулю (формула 2.15 и 2.16): 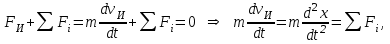 (2.15) (2.15)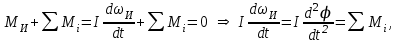 (2.16) (2.16)где 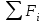 – сумма всех сил, действующих на твердое тело; – сумма всех сил, действующих на твердое тело;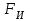 , , 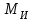 – сила инерции и момент от сил инерции твердого тела; – сила инерции и момент от сил инерции твердого тела;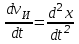 – ускорение твердого тела; – ускорение твердого тела;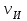 – скорость; – скорость;х – перемещение; φ, ω– угол поворота и угловая скорость барабана. |
