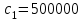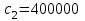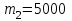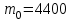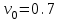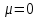Диссертация Повышение безопасной эксплуатации башенных кранов. диссертация. Асанхан Жаннур Оразханлы повышение безопасности эксплуатации стреловых кранов за счет снижения динамических нагрузок при подъёме груза магистерская диссертация

Название	Асанхан Жаннур Оразханлы повышение безопасности эксплуатации стреловых кранов за счет снижения динамических нагрузок при подъёме груза магистерская диссертация
Анкор	Диссертация Повышение безопасной эксплуатации башенных кранов
Дата	27.05.2022
Размер	1.74 Mb.
Формат файла
Имя файла	диссертация.docx
Тип	Диссертация #552335
страница	4 из 4

1 2 3 4

3.2 Исследование поведения крана при подъеме груза в абсолютно-упругой системе
Исследование заданного физического процесса будет выполняться в виде эксперимента в программной среде MathCad.

Сущность эксперимента состоит в том, что в математической модели механизма подъема груза, будет изолирован вязкий элемент.

Эксперимент 1. Процесс подъема груза краном «с подхватом», без применения вязкого элемента.

Шаг 1. Запись исходных данных (таблица 3.2).
Таблица 3.2

Исходные данные

Исходные данные и принятые обозначения
Коэффициент жёсткости канатов, Н/м
Коэффициент жесткости металлоконструкции крана, Н/м
Масса груза, кг
Масса крана приведенная к оголовку стрелы, кг
Скорость наматывания каната на барабан, м/с
Коэффициент демпфирования модели Фойгта, Н/м

Шаг 2. Подставив исходные данные в математическую модель, получим следующие графические изображения результатов эксперимента (рисунок 3.5, 3.6):

1 – перемещение; 2 – скорость перемещения; 3 – ускорение перемещения
Рисунок 3.5 – Графики изменения перемещения, скорости перемещения, ускорения перемещения приведенной массы крана к оголовку стрелы в зависимости от времени (без применения вязкого элемента)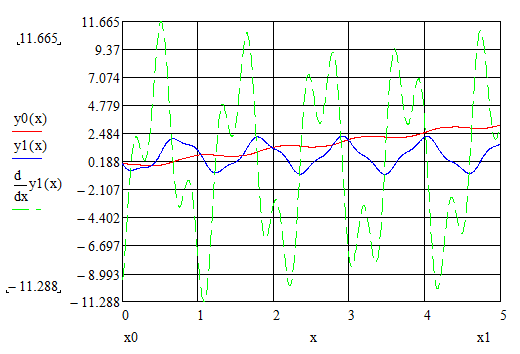

1 – перемещение; 2 – скорость перемещения; 3 – ускорение перемещения
Рисунок 3.6 – Графики изменения перемещения, скорости перемещения, ускорения перемещения массы груза в зависимости от времени (без применения вязкого элемента)

Далее предполагается провести анализ по подобию анализа решения математической модели с вязким элементом, то есть каждый из полученных графиков условно разделяются на составные части:

1. Анализ графика изменения перемещения, скорости перемещения, ускорения перемещения приведенной массы крана к оголовку стрелы в зависимости от времени (без вязкого элемента)

Рисунок 3.7 – Составная часть графиков изменения перемещения, скорости перемещения, ускорения перемещения приведенной массы крана к оголовку стрелы в зависимости от времени
В точке 1 как видно из рисунка 3.7, значение скорости увеличивается, соответственно увеличиваются и ускорение, и перемещение. Стоит отметить, что ускорение обретает изначально максимальное значение приблизительно равное 9.5 м/с², затем резко снижается, в точке 1 обретая значение чуть больше единицы, это обусловлено тем, что скорость достигая определенного значения в какой-то момент имеет постоянную величину.

В промежутке точек 1 и 2, наблюдается уже снижение скорости, достигая минусового значения, затем снова увеличивается и уже в точке 2 обретает значение нуля. Ускорение в данной точке в соответствии законам кинематики так же становится равным нулю. Перемещение оголовка стрелы имеет постоянную величину, ввиду того что скорость и ускорение достигли значения нуля.

Далее от точки 2 к точке 3 скорость и ускорение в этом промежутке достигли минусового значения, соответственно значение перемещения оголовка стрелы снижается до нуля.

В промежутке точек 3 и 4 наблюдается разгон системы соответственно нарастают скорость и ускорение. Перемещение в этом моменте остается практически неизменным.

Таким образом, стоит отметить, что вся система без вязкого элемента имеет резонансный характер колебаний.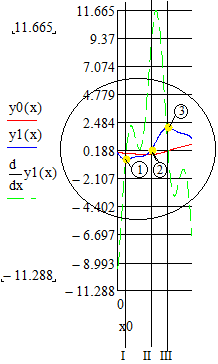

Рисунок 3.8 – Составная часть графиков изменения перемещения, скорости перемещения, ускорения перемещения массы груза в зависимости от времени
В точке 1 отрывная стадия груза, который в этот момент обретает скорость значение которого, исходя из рисунка 3.8 минусовое, с возникновением скорости и возникает ускорение, которое заметно сначала обретает минусовое значение, затем резко достигает значения скорости в точке 1. Что касается перемещения груза, то оно минимальное, так как в данной точке идет отрывная стадия.

В промежутке точек 1 и 2, увеличивается скорость соответственно и ускорение, но стоит отметить, что в определённый момент скорость постоянна следовательно ускорение в этот момент равно нулю. Далее скорость и ускорение перемещения груза, нарастают, возникает небольшое перемещение груза.

Промежуток точек 2 и 3 вся система нарастает идет резкое увеличение скорости, колоссально растет значение ускорение, соответственно и нарастает перемещение.

Анализ составляющей данного графика, сводится к тому, что в отрывной стадии груза, резко снижается скорость подъема груза. В послеотрывной стадии наблюдается колебание груза, перемещение которого очень затруднено ввиду особенности выбора режима работы крана.

Таким образом, анализ результатов эксперимента соответствует физической действительности. Наглядно отражая сущность отсуствия вязкого элемента.

Для более наглядного результата сущности применения вязкого элемента в математической модели механизма подъема груза краном, предлагается расчет коэффициента динамичности системы.

По полученным всем численным данным скорости и ускорения перемещения оголовка стрелы башенного крана и груза вычисляются коэффициенты динамичности (формула 3.1). Для расчетов предлагается выбрать максимальные значения ускорения всех систем.

, (3.1)

К_д1=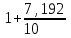

=1,7192
К_д2=

=2,2293
где Р_дин– динамические нагрузки;

Р_ст– статические нагрузки;

Р_а– инерционная нагрузка;

a – максимальное значение ускорения перемещения оголовка стрелы, м/с²;

m – масса поднимаемого груза;

g – ускорение свободного падения (g = 9.8 м/с2

10 м/с²);

К_д1– коэффициент динамичности, при работе крана с применением вязкого элемента;

К_д2– коэффициент динамичности, при работе крана без применения вязкого элемента.
Далее после получения результатов расчета коэффициента динамичности, для наглядного отражения сущности вязкого элемента предлагается расчет отношений данных показателей (формула 3.2):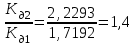

Таким образом, результат отношения показателей, отражает сущность вязкого элемента. То есть, при подъеме груза башенным краном «с подхватом», с применением вязкого – диссипативного элемента позволит снизить динамические нагрузки системы в 1.4 раза, тем самым считается, что цели и задачи исследования достигнуты.

По полученным результатам экспериментов математического моделирования как было упомянуто в главе 1 подпункте 1.2, предлагается выработка рекомендации по усовершенствованию конструкции крана, а именно крюковой подвески, описание которого представлено ниже.

Принцип работы предлагаемого технического решения (рисунок 3.8) заключается в том, что предлагается упругая крюковая подвеска, которая состоит из двух листовых щёк 9, двух осей, на которых на шарикоподшипниках 6, 11 установлен блок 12, траверса 3 и пропущенного через неё крюка 1. Щёки стянуты между собой болтами с распорными трубками. Крюк опирается на траверсу через упорный шарикоподшипник и может вращаться относительно траверсы и щёк подвески. Такое крепление позволяет разворачивать поднятый груз вокруг вертикальной оси подвески. Подшипник крюка закрыт от грязи и влаги крышкой и резиновыми уплотнителями. На крюк установлен предохранительный замок 2, который при работе препятствует произвольному выходу серьги съёмного грузозахватного приспособления из зёва крюка.

Идея предлагаемого изобретения заключается в том что, при нагружении крюковой подвески крана грузом, в случае резкого снятия нагрузки возникают резонансные частоты колебания всей конструкции крана, которые могут повлечь за собой аварийные ситуации. Ввиду этого в упругой крюковой подвеске крана предусмотрено применение демпфирующих и диссипативных элементов, которые позволят достичь затухания резонансных колебаний в точке их возникновения. Достижение такого результата обусловлено особенностью свойств демпфирующих и диссипативных элементов и конструкции крюковой подвески.

Крюковая подвеска так же включает в себя упругий, вязкий элементы и выходящий за пределы корпуса шток с грузозахватным органом 1. Вязкий и упругий элементы закреплены на опорных шайбах опирающиеся на нижнем и верхнем шарикоподшипниках. Вязкий элемент 5 выполнен в виде симметрично расположенных 2-х цилиндров шток, поршень и цилиндрический корпус. Пространство под поршнем заполнено гидравлической жидкостью. Упругий элемент 4 представляет с собой цилиндрически винтовую пружину, расположенный парно-симметрично вязкому элементу. Результатом расположения элементов является, равномерное распределение динамических усилий, возникающих при эффективном использовании упругой подвески.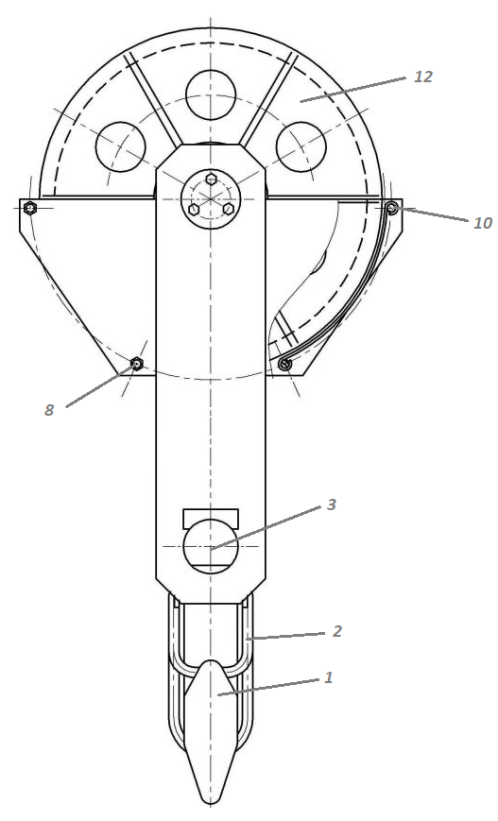

Рисунок 3.8 – Схема упругой крюковой подвески общий вид
1 – грузозахватный орган; 2 – предохранительный замок; 3 – траверса; ; 4 – упругий элемент; 5 – вязкий элемент; 6, 11 – шарикоподшипники; 7 – удерживающая гайка; 9 – корпусные щеки; 8, 10 – втулки; 12 – блок

Заключение
В первой главе магистерской диссертации были тщательно проанализированы статистики по авариям грузоподъемных кранов и причины спровоцировавших эти самые аварий. Так же были описаны характеристика режимов и способов ведения работы на кранах. По итогам первой главы удостоверено, что больше всего аварий по грузоподъемным кранам приходятся на башенные краны, причинам которых по большей мере степени являются динамические колебания, возникающие при подъеме груза.

Во второй главе описано назначение и основы математического моделирование, далее поэтапно описаны процессы математического моделирование механизма подъема груза башенным краном в среде MathCad. Решение дифференциальных уравнении, в среде MathCad, предполагается с использованием функцией odesolve методом Рунге–Кутты. В свою очередь встроенная функция odesolve предназначена для решения дифференциальных уравнений, линейных относительно старшей производной.

В третьей главе представлены описания проведения экспериментов в среде MathCad. В результате экспериментов, получены графики, наглядно отражающие сущность применения модели Фойгта в механизме подъёма груза.

Подробно описана выработка рекомендации по усовершенствованию конструкции крана, крюковой подвески. Идея усовершенствования конструкции крана заключается в том что, при нагружении крюковой подвески крана грузом, в случае резкого снятия нагрузки возникают резонансные частоты колебания всей конструкции крана, которые могут повлечь за собой аварийные ситуации. Ввиду этого в упругой крюковой подвеске крана предусмотрено применение демпфирующих и диссипативных элементов, которые позволят достичь затухания резонансных колебаний в точке их возникновения.

По итогам всей научно-исследовательской работы, считается что задачи и цели исследования достигнуты.

Список используемой литературы
1. Башенные краны [сайт] URL: / © 2000 – 2016, ООО «Олбест». / URL: http://knowledge.allbest.ru/construction/3c0b65635a3ac68b4d43b88521216d27_0.html#text;

2. Устойчивость стационарных башенных кранов в условиях ветрового нагружения [сайт] URL: https://www.dissercat.com/content/ustoichivost–statsionarnykh–bashennykh–kranov–v–usloviyakh–vetrovogo–nagruzheniya;

3. Состояние вопроса динамики башенных кранов с учетом больших перемещений [сайт] URL: https://cyberleninka.ru/article/v/sostoyanie–voprosa–dinamiki–bashennyh–kranov–s–uchetom–bolshih–peremescheniy;

4. Эксплуатация грузоподъёмных кранов [сайт] URL: http://mipk.by/news–fpb/378–jekspluatacija–gruzopodemnyh–kranov.html (дата обращения 18.01.2018);

5. Проблема травматизма и возникновения аварийных ситуаций при эксплуатации автомобильных кранов [сайт] URL: https://botan.cc/prepod/dop_obrazovanie/otss5qgu.htm (дата обращения 18.01.2018);

6. Состояние аварийности и травматизма
при эксплуатации опасных производственных объектов,
на которых используются подъемные сооружения [сайт] URL: https://prominf.ru/article/sostoyanie–avariynosti–i–travmatizma–pri–ekspluatacii–opo–na–kotoryh–ispolzuetsya;

7. Безопасность погрузоразгрузочных работ кранами [сайт] URL: http://www.bestreferat.ru/referat–242426.html;

8. Основные причины аварий башенных кранов и меры для их устранения [сайт] URL: http://www.lobzikov.ru/news/osnovnye–prichiny–avariy–bashennyh–kranov–i–mery–293;

9. Математическая модель подъёма груза башенным краном [сайт] URL: http://docplayer.ru/72272908–Matematicheskaya–model–podyoma–gruza–bashennym–kranom.html;

10. Вайнсон А.А. Подъёмно–транспортные машины: учебник для вузов / А.А. Вайнсон. М.:Машиностроение,1989.–536с.;

11. Математическое моделирование [сайт] URL: http://storage.mstuca.ru/bitstream/123456789/7730/2/%D0%9C.pdf;

12. Моделирование как метод научного познания [сайт] URL: http://www.myshared.ru/slide/1243144/;

13. Введение в математичское моделирование [сайт] URL: http://docplayer.ru/51189286–Vvedenie–v–matematicheskoe–modelirovanie.html;

14. Основы математического моделирования [сайт] URL: http://math.phys.msu.ru/data/27/OMM1.pdf;

15. Моделирование как основной компонент наглядного обучения математике инженеров–бакалавров [сайт] URL: https://www.top–technologies.ru/ru/article/view?id=35573;

16. Моделирование физическое [сайт] URL: http://economy–ru.info/info/3096/;

17. Идеальные и материальные модели [сайт] URL: http://systems–analysis.ru/model_am.html;

18. Тарасик В.П. Математическое моделирование технических систем: Учебник / Тарасик В.П. – М.:НИЦ ИНФРА–М, 2016. – 592 с;

19.Основы планирования эксперимента [сайт]URL: http://window.edu.ru/resource/438/18438/files/Mtdukm8.pdf;

20. Планирование экспериента [сайт] URL: https://ru.wikipedia.org/wiki/%D0%9F%D0%BB%D0%B0%D0%BD%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D1%8D%D0%BA%D1%81%D0%BF%D0%B5%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D1%82%D0%B0;

1 2 3 4