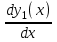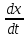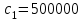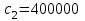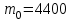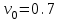Диссертация Повышение безопасной эксплуатации башенных кранов. диссертация. Асанхан Жаннур Оразханлы повышение безопасности эксплуатации стреловых кранов за счет снижения динамических нагрузок при подъёме груза магистерская диссертация
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
2.2 Система дифференциальных уравнений, описывающая подъём груза В соответствии с содержательной постановкой задачи расчетная схема механизма подъёма выглядит следующим образом (рисунок 2.5). Для достижения цели исследования данной работы, было принято решение исследовать механизм подъема груза «с подхватом». При подъеме груза «с подхватом» предполагается, что груз лежит на каком–либо основании, канаты провисают и, следовательно, в этот момент нагрузка на грузозахватный орган и канатный полиспаст равна нулю. Динамическая нагрузка возникает в период, когда к подъемному полиспасту и грузозахватному органу, движущимся с номинальной скоростью подъема груза v0, будет мгновенно приложен вес груза. Тогда номинальная скорость подъема груза v0 является постоянной физической величиной, v0 – const, так же считается, что канаты абсолютно жесткие, следовательно, не упругая система. В соответствии с содержательной постановкой задачи расчетная схема механизма подъёма выглядит следующим образом (рисунок 2.6). 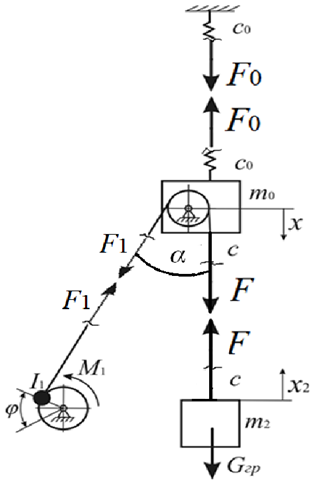 m0 – приведенная к оголовку стрелы масса крана; I1 – приведенный к барабану момент инерции привода; m2 - масса груза; с0 – жесткость металлоконструкции крана; с – жесткость канатов полиспаста; Gгр – вес груза; М1 – момент двигателя Рисунок 2.6 – Расчетная схема механизма подъёма В результате преобразовании всех выражений система дифференциальных уравнений механизма подъема груза выглядит следующим образом (формула 2.17):  (2.17) (2.17)где  – масса груза; – масса груза; – приведенная масса крана; – приведенная масса крана;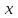 – деформация конструкции крана; – деформация конструкции крана;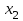 – деформация каната. – деформация каната. В соответствии с целью научно-исследовательской работы предлагается внедреить упругую крюковую подвеску в конструкцию крана, таким образом расчетная схема механизма подъема груза будет выглядить следующим образом (рисунок 2.7). 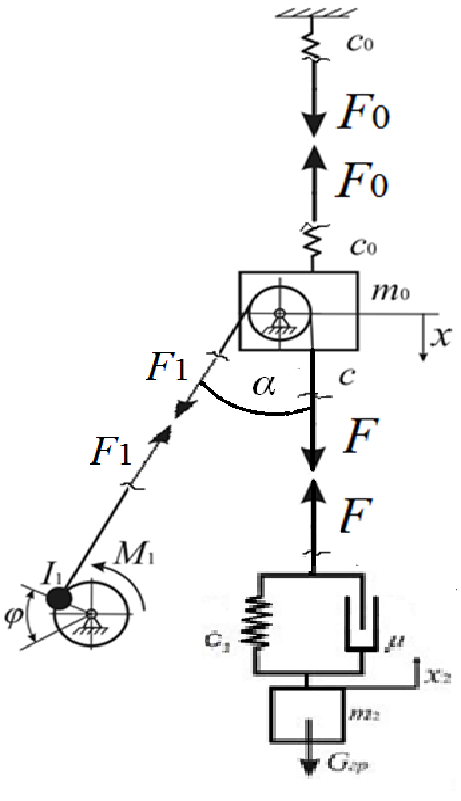 m0 – приведенная к оголовку стрелы масса крана; I1 – приведенный к барабану момент инерции привода; m2 - масса груза; с0 – жесткость металлоконструкции крана; с1 – жесткость канатов полиспаста; с2 – жесткость упругого элемента;  – коэффициент вязкости диссипативного элемента; Gгр – вес груза; М1 – момент двигателя – коэффициент вязкости диссипативного элемента; Gгр – вес груза; М1 – момент двигателяРисунок 2.7 – Модифицированная расчетная схема механизма подъёма Данная схема была получена путем применения модели Фойгта (рисунок 2.8).  Рисунок 2.8 – Модель Фойгта Как видно из схемы модель состоит из параллельно соединненых упругого и диссипативного элементов. При таком соединении деформация элементов будет одна и та же, а общее напряжение состоит из суммы напряжений в правой и левой ветви  , так как напряжение есть сила, приходящаяся на единицу площади, то можно записать, что в данной модели , так как напряжение есть сила, приходящаяся на единицу площади, то можно записать, что в данной модели 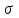 = Fkтогда, усилие Fk возникающее при деформации всей модели бдует выглядит следующим образом формула 2.18: = Fkтогда, усилие Fk возникающее при деформации всей модели бдует выглядит следующим образом формула 2.18: (2.18) (2.18)Компонентные уравнения (формула 2.19, 2.20) системы дифференциальных уравнений (формула 2.17) будут записываться так:  (2.19) (2.19) (2.20) (2.20)В конечном итоге подставив компонентные уравнения в систему дифференциальных уравнений получим (формула 2.21): 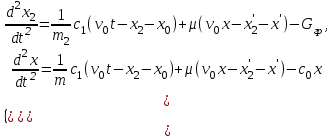 (2.21) (2.21)Полученную систему дифференциальных уравнений – математическую модель механизма подъема груза «с подхватом» предлагается моделировать в среде MathCad. 2.3 Моделирование динамики башенного крана в среде MathCad MathCad – это программное обеспечение для инженерных расчетов позволяет представлять свои расчеты с помощью диаграмм, графиков, текста и изображений в едином документе. Решение дифференциальных уравнении, в среде MathCad, предполагается с функцией odesolve методом Рунге–Кутты. В свою очередь встроенная функция odesolve предназначена для решения дифференциальных уравнений, линейных относительно старшей производной. В отличие от других функций библиотеки Differential Equation Solving, odesolve решает дифференциальные уравнения, записанные в общепринятом в математической литературе виде. Прежде всего для работы в програмной среде необходимо выполнить ряд шагов. Шаг 1. Составление идентификационной таблицы (таблица 2.1). Таблица 2.1 Идентификационная таблица данных уравнений
Далее после того как были записаны данные и их обозначения, вводим в программу вычислительный блок. Шаг 2. Начальные условия. 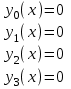 Шаг 3. Вычислительный блок дифференциальных уравнений Подразумевает запись математической модели механизма подъема груза в программную среду в соответствии с идентификационной таблицей (таблицы 2.1). Таким образом, математическая модель будет выглядеть так: Given (Дано): 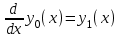 (2.22) (2.22)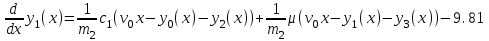 (2.23) (2.23) (2.24) (2.24)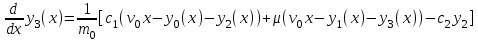 (2.25) (2.25)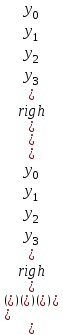 Определение усилия в канате (формула 2.26). 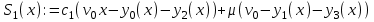 (2.26) (2.26)Таким образом, выстроив, математическую модель механизма подъема груза башенным краном предполагается провести исследования взаимосвязи поведения крана с применением модели Фойгта и без нее, путем постановки экспериментов в программе MathCad. 3. Планирование и постановка научного эксперимента Эксперимент – целенаправленное воздействие на объект исследования с целью получения достоверной информации [19]. Планирование эксперимента (англ. experimental design techniques) – комплекс мероприятий, направленных на эффективную постановку опытов. Основная цель планирования эксперимента – достижение максимальной точности измерений при минимальном количестве проведенных опытов и сохранении статистической достоверности результатов [20]. Большинство научных исследований связано с экспериментом. Он проводится на производстве, в лабораториях, на опытных полях и участках, в клиниках и т.д. Эксперимент может быть физическим, психологическим или модельным. Он может непосредственно проводиться на объекте или на его модели. Модель обычно отличается от объекта масштабом, а иногда природой. Главное требование к модели – достаточно точное описание объекта. В последнее время наряду с физическими моделями все большее распространение получают абстрактные математические модели. К слову, планирование эксперимента напрямую связано с разработкой и исследованием математической модели объекта исследования [19]. 3.1 Результаты математического моделирования Для достижения результатов решения математической модели предполагается применение следующих исходных данных, значение которых были заданы в соответствии с особенностью физических параметров (таблица 3.1). Таблица 3.1 Исходные данные
Таким образом, после подстановки исходных данных в модель, были получены следующие результаты решения (рисунок 3.1,3.2).  1 – перемещение; 2 – скорость перемещения; 3 – ускорение перемещения Рисунок 3.1 – Графики изменения перемещения, скорости перемещения, ускорения перемещения приведенной массы крана к оголовку стрелы в зависимости от времени  1 – перемещение; 2 – скорость перемещения; 3 – ускорение перемещения Рисунок 3.2 – Графики изменения перемещения, скорости перемещения, ускорения перемещения массы груза в зависимости от времени После достижения результатов решения, предполагается провести их анализ на соответствие с физическим смыслом. Для этого каждый из полученных графиков условно разделяются на составные части: 1. Анализ графика изменения перемещения, скорости перемещения, ускорения перемещения приведенной массы крана к оголовку стрелы в зависимости от времени. 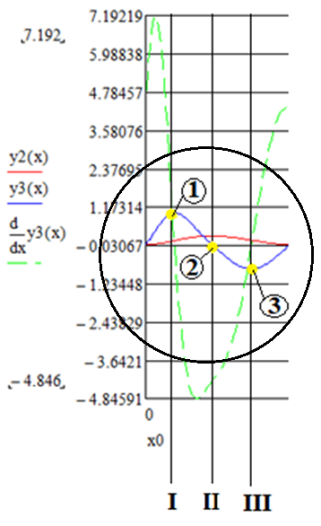   , Рисунок 3.3 – Составная часть графиков изменения перемещения, скорости перемещения, ускорения перемещения приведенной массы крана к оголовку стрелы в зависимости от времени Как видно на рисунке 3.3, отмечены точки 1, 2, 3, каждая из которых имеет определенный характер физического процесса. В точке 1, наблюдается возрастание скорости перемещения, соответственно возрастает и само перемещение оголовка стрелы. Ускорение в данной точке приближено к значению нуля, в связи с тем, что скорость перемещения в какой-то момент имеет постоянную величину. В промежуток между точками 1 и 2 заметно снижается скорость перемещения оголовка стрелы, соответственно ускорение в данный промежуток обретает минусовое значение. В точке 2, скорость перемещения принимает значение нуля, о чем свидетельствует перемещение оголовка стрелы, которое принимает, в этот момент, постоянную величину. В промежутке точек 2 и 3 скорость приобретает минусовое значение, как и ускорения, в то время как значение перемещения с точки 2 в точку 3 уменьшается соответственно. Таким образом, результаты решения математической модели соответствуют с физическим описанием процессов. 2. Анализ графиков изменения перемещения, скорости перемещения, ускорения перемещения массы груза в зависимости от времени.  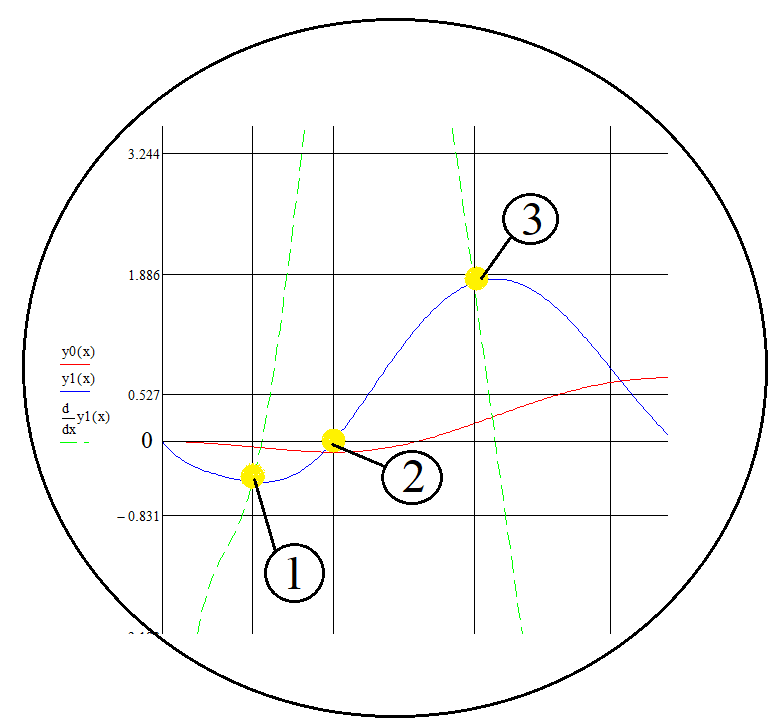  , Рисунок 3.4 – Составная часть графиков изменения перемещения, скорости перемещения, ускорения перемещения массы груза в зависимости от времени Как представлено на рисунке 3.4 так же, отмечены три точки, каждая из которых характеризует определенный момент, физического процесса. В точке 1 скорость перемещения массы груза приобретает минусовое значение, соответственно перемещение груза так же имеет минусовое значение, в этот момент ускорение перемещения пересекается с кривой скорости и имеет приблизительно то же численно значение. В промежутке точек 1 и 2 в определенный момент скорость перемещения обретает постоянную величину, в то время как ускорение согласно второму закону Ньютона, будет равным нулю. Далее скорость перемещения груза постепенно увеличивается, как и само перемещение и в точке 2 обретает значение равное нулю. В промежутке точек 2 и 3 наглядно представлено резкое нарастание скорости и достигает значения 1.8 м/с, ускорение согласно законам физики, так же резко увеличивается, что же касается перемещения соответственно оно тоже увеличивается как и скорость. В точке 3, где скорость достигла максимального значения, ускорение перемещения груза обретает то же значение что и скорость, затем заметно снижается до нуля, так как в определённый момент скорость приобретает снова постоянную величину. Характеризуя поведение графиков физических параметр, можно прийти к выводу, что все показатели соответствуют кинематическим и динамическим законам физики. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||