АДПЭ. АДПЭ с циферками. aвременным рядом
 Скачать 303.21 Kb. Скачать 303.21 Kb.
|
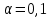 . Начальный параметр S0 принять равным средней арифметической первых трех уровней временного ряда. . Начальный параметр S0 принять равным средней арифметической первых трех уровней временного ряда.[a]258 [a]259 [a]260 [a]261 [a]262 160[q]1:1:При каком параметре сглаживания в методе экспоненциальной средней будет получен более гладкий временной ряд? [a]0,1 [a]0,2 [a]0,3 [a]0,4 [a]0,5 161[q]2:1:По данным выпуска продукции фирмы за восемь лет было получено уравнение линейного тренда 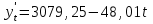 . Найти прогнозное значение выпуска продукции в следующем году. . Найти прогнозное значение выпуска продукции в следующем году.[a]3079,25 [a]3423,12 [a]2647,16 [a]3321,24 [a]3210,37 162[q]3:1:По данным выпуска продукции фирмы за восемь лет было получено уравнение параболического тренда 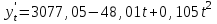 . Найти прогнозное значение выпуска продукции в следующем году. . Найти прогнозное значение выпуска продукции в следующем году.[a]3079,25 [a]3423,12 [a]2647,16 [a]3321,24 [a]2653,47 163[q]2:1:По данным о численности студентов заочной формы обучения ВУЗа за пять лет было получено уравнение линейного тренда 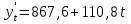 . Найти прогнозное значение численности студентов в следующем году. . Найти прогнозное значение численности студентов в следующем году.[a]1532,4 [a]1643,3 [a]1592,5 [a]1679 [a]1766,1 164[q]2:1:По данным о численности студентов заочной формы обучения ВУЗа за пять лет было получено уравнение линейного тренда 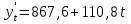 . Какая численность студентов ожидается через два года? . Какая численность студентов ожидается через два года?[a]1532,5 [a]1643,2 [a]1592,5 [a]1679 [a]1766,1 165[q]1:1:В модели экспоненциального сглаживания параметр сглаживания может быть равен: [a]0,3 [a]0 [a]-0,3 [a]-1 [a]1 166[q]1:1:В модели экспоненциального сглаживания параметр сглаживания не может быть равен: [a]0,9 [a]0,3 [a]0,5 [a]0,7 [a]1,0 167[q]3:1:При расчете экспоненциальной средней 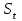 для временного ряда прибыли компании параметр сглаживания для временного ряда прибыли компании параметр сглаживания 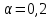 , , 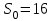 . .
Экспоненциальная средняя 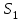 равна: равна:[a]16,5 [a]16,1 [a]15,9 [a]16,7 [a]17,0 168[q]3:1:При расчете экспоненциальной средней 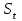 для временного ряда прибыли компании параметр сглаживания для временного ряда прибыли компании параметр сглаживания 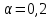 , , 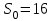 . .
Экспоненциальная средняя 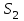 равна: равна:[a]16,08 [a]16,12 [a]15,34 [a]16,75 [a]16,50 169[q]2:1:Факторная дисперсия в однофакторном дисперсионном анализе вычисляется по формуле: [a] 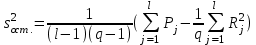 , где , где 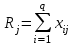 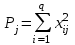 [a] 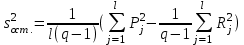 , где , где 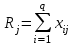 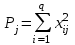 [a] 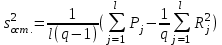 , где , где 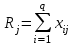 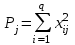 [a] 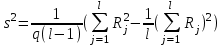 , где , где 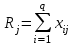 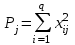 [a] 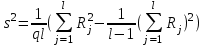 , где , где 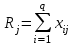 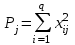 170[q]2:1:Остаточная дисперсия в однофакторном дисперсионном анализе вычисляется по формуле: [a] 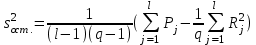 , где , где 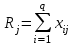 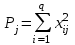 [a] 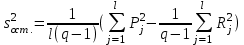 , где , где 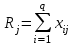 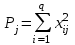 [a] 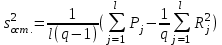 , где , где 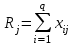 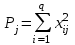 [a] 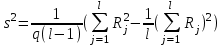 , где , где 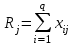 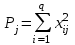 [a] 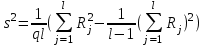 , где , где 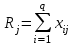 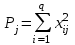 171[q]1:1:При каком условии в однофакторном дисперсионном анализе следует сразу сделать вывод об отсутствии существенного влияния фактора А на величину Х. [a] 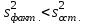 [a] 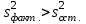 [a] 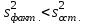 [a] 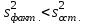 [a] 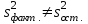 172[q]3:1:Проведены измерения для каждого из трех уровней некоторого фактора А. Найти факторную дисперсию, используя метод однофакторного дисперсионного анализа.
[a]5,6 [a]7,6 [a]4,2 [a]8,1 [a]9,4 173[q]3:1:Проведены измерения для каждого из трех уровней некоторого фактора А. Найти факторную дисперсию, используя метод однофакторного дисперсионного анализа.
[a]5,6 [a]7,6 [a]4,2 [a]8,1 [a]2,7 174[q]3:1:Проведены измерения для каждого из трех уровней некоторого фактора А. Найти факторную дисперсию, используя метод однофакторного дисперсионного анализа.
[a]13,4 [a]18,6 [a]15,7 [a]11,6 [a]12,8 175[q]3:1:Проведены измерения для каждого из трех уровней некоторого фактора А. Найти остаточную дисперсию, используя метод однофакторного дисперсионного анализа.
[a]5,1 [a]3,4 [a]2,2 [a]1,5 [a]4,7 176[q]1:1:Функция расстояний в кластерном анализе, определяемая формулой 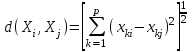 , называется: , называется:[a]метрикой l1 [a]lp - нормой [a]евклидовой метрикой [a]манхэттенским расстоянием [a]расстоянием Чебышева 177[q]1:1:Функция расстояний в кластерном анализе, определяемая формулой 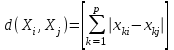 , называется: , называется:[a]метрикой l1 [a]lp - нормой [a]евклидовой метрикой [a]манхэттенским расстоянием [a]расстоянием Чебышева 178[q]1:1:Функция расстояний в кластерном анализе, определяемая формулой 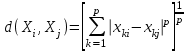 , называется: , называется:[a]метрикой l1 [a]lp - нормой [a]евклидовой метрикой [a]манхэттенским расстоянием [a]расстоянием Чебышева 179[q]2:1:Формула расчета расстояний между кластером r, представляющим результат объединения кластера l и m, с кластером q, методом «ближнего соседа»: [a] 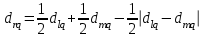 [a] 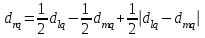 [a] 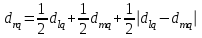 [a] 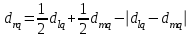 [a] 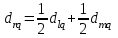 180[q]2:1:Формула расчета расстояний между кластером r, представляющим результат объединения кластера l и m, с кластером q, методом «дальнего соседа»: [a] 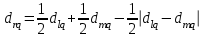 [a] 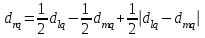 [a] 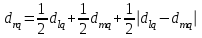 [a] 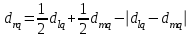 [a] 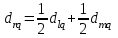 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
