АДПЭ. АДПЭ с циферками. aвременным рядом
 Скачать 303.21 Kb.
|
|
у3: [a]15,4 [a]15,0 [a]13,3 [a]16,7 [a]17,1 140[q]2:1:По данным об урожайности зерновых культур (ц/га) за 10 лет:
Рассчитайте четырехлетнюю скользящую среднюю простую у3: [a]14,75 [a]15,50 [a]15,125 [a]16,50 [a]17,25 141[q]2:1:Основные предпосылки дисперсионного анализа: [a]Зависимость переменной yi есть величина случайная, а объясняющая переменная xi неслучайная; математическое ожидание возмущения равно 0 для любых εij [a]Дисперсия переменной xij постоянна для любых i, j; переменная xij не имеет нормальный закон распределения, переменные yi и yj некоррелированны [a]Математическое ожидание возмущения равно 0 для любых εij; возмущения εIj взаимно независимы; дисперсия переменной xij постоянна для любых i, j; переменная xij имеет нормальный закон распределения [a]Дисперсия зависимой переменной xij постоянна для любых i, j; зависимость переменной yi есть величина случайная, а объясняющая переменная xi неслучайная [a]Зависимость переменной yi есть величина случайная, а объясняющая переменная xi неслучайная; переменная xij не имеет нормальный закон распределения, переменные yi и yj некоррелированны 142[q]1:1:Многомерные методы статистического анализа: [a]Планирование и оценка эффективности финансово-кредитных операций, расчет страховых аннуитетов, планирование погашения долгосрочных задолжностей [a]Корреляционный анализ, спектральный анализ [a]Факторный анализ, метод главных компонентов, спектральный анализ [a]Расчет страховых аннуитетов, Факторный анализ, корреляционный анализ [a]Факторный анализ, метод главных компонентов, дискриминантный анализ, кластерный анализ 143[q]1:1:Основная задача дисперсионного анализа: [a]выявление, идентификация и сравнение однородности групп по общности наблюдаемых объектов [a]разбиение множества исследуемых объектов и признаков на однородные в соответствующем понимании группы [a]переход первоначальной системы большого числа взаимосвязанных факторов относительно малому числу скрытых, латентных факторов [a]изучение влияния одного или нескольких факторов на рассматриваемый признак [a]на основе множества внешних признаков найти небольшое, но значимое число их гибридов 144[q]1:1:Основная задача дискриминантного анализа: [a]выявление, идентификация и сравнение однородности групп по общности наблюдаемых объектов [a]разбиение множества исследуемых объектов и признаков на однородные в соответствующем понимании группы [a]переход первоначальной системы большого числа взаимосвязанных факторов относительно малому числу скрытых, латентных факторов [a]изучение влияния одного или нескольких факторов на рассматриваемый признак [a]на основе множества внешних признаков найти небольшое, но значимое число их гибридов 145[q]1:1:Основная задача кластерного анализа: [a]выявление, идентификация и сравнение однородности групп по общности наблюдаемых объектов [a] разбиение множества исследуемых объектов и признаков на однородные в соответствующем понимании группы [a]переход первоначальной системы большого числа взаимосвязанных факторов относительно малому числу скрытых, латентных факторов [a]изучение влияния одного или нескольких факторов на рассматриваемый признак [a]на основе множества внешних признаков найти небольшое, но значимое число их гибридов 146[q]1:1:Основная задача факторного анализа: [a]выявление, идентификация и сравнение однородности групп по общности наблюдаемых объектов [a]разбиение множества исследуемых объектов и признаков на однородные в соответствующем понимании группы [a] переход первоначальной системы большого числа взаимосвязанных факторов относительно малому числу скрытых, латентных факторов [a]изучение влияния одного или нескольких факторов на рассматриваемый признак [a]на основе множества внешних признаков найти небольшое, но значимое число их гибридов 147[q]1:1:Основная задача компонентного анализа: [a]выявление, идентификация и сравнение однородности групп по общности наблюдаемых объектов [a]разбиение множества исследуемых объектов и признаков на однородные в соответствующем понимании группы [a]переход первоначальной системы большого числа взаимосвязанных факторов относительно малому числу скрытых, латентных факторов [a]изучение влияния одного или нескольких факторов на рассматриваемый признак [a]на основе множества внешних признаков найти небольшое, но значимое число их гибридов 148[q]1:1:Что такое сезонная компонента временных рядов? [a]плавноменяющаяся компонента, описывающая чистое влияние долговременных факторов, т.е. длительную тенденцию изменения признака [a]компонента, отражающая повторяемость экономических процессов в течение не очень длительного периода [a]компонента, отражающая повторяемость экономических процессов в течение длительного периода [a]компонента, отражающая влияние не поддающихся учету и регистрации случайных компонентов [a]показатель, отражающий отставание или опережение во времени одного явления, по сравнению с другим 149[q]1:1:Что такое циклическая компонента временных рядов? [a]плавноменяющаяся компонента, описывающая чистое влияние долговременных факторов, т.е. длительную тенденцию изменения признака [a]компонента, отражающая повторяемость экономических процессов в течение не очень длительного периода [a]компонента, отражающая повторяемость экономических процессов в течение длительного периода [a]компонента, отражающая влияние не поддающихся учету и регистрации случайных компонентов [a]показатель, отражающий отставание или опережение во времени одного явления, по сравнению с другим 150[q]1:1:В каких случаях используется метод сложения сезонных колебаний при прогнозировании временных рядов? [a]Когда сезонные составляющие относительно постоянны по всему анализируемому временному периоду [a]Когда сезонные составляющие не постоянны по всему анализируемому ряду [a]Когда сезонные составляющие изменяются пропорционально значениям тренда по всему анализируемому временному периоду [a]Когда сезонные составляющие не изменяются [a]Незначительная вариация цепных абсолютных приростов 151[q]1:1:В каких случаях используется метод умножения сезонных колебаний при прогнозировании временных рядов? [a]Когда сезонные составляющие относительно постоянны по всему анализируемому временному периоду [a]Когда сезонные составляющие не постоянны по всему анализируемому ряду [a]Когда сезонные составляющие изменяются пропорционально значениям тренда по всему анализируемому временному периоду [a]Когда сезонные составляющие не изменяются [a]Незначительная вариация цепных абсолютных приростов 152[q]1:1:Классификация объекта на основе его различных характеристик, отнесение его к одной из нескольких групп некоторым оптимальным способом, является целью: [a]компонентного анализа [a]корреляционного анализа [a]дискриминантного анализа [a]факторного анализа [a]регрессионного анализа 153[q]1:1:Какой критерий используется для проверки значимости различия двух дисперсий? [a]Критерий Стьюдента [a]Критерий Пирсона [a]Критерий Дарбина-Уотсона [a]Критерий Фишера [a]Критерий Голдфелда-Квандта 154[q]1:1:Какой анализ применяют для изучения влияния факторов, характеризующиеся несколькими уровнями? [a]кластерный анализ [a]однофакторный дисперсионный анализ [a]дисперсионный анализ [a]факторный анализ [a]дискриминантный анализ 155[q]1:1:Модель экспоненциального сглаживания определяется рекуррентной формулой: [a] 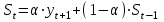 [a] 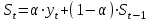 [a] 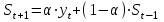 [a] 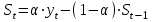 [a] 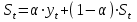 156[q]3:1:Временной ряд квартальной динамики прибыли компании сглаживается с использованием экспоненциальной средней.
Найти сглаженное значение второго уровня, приняв параметр сглаживания 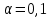 . Начальный параметр S0 принять равным средней арифметической первых трех уровней временного ряда.[a]9,8 [a]10,1 [a]10,2 [a]11,1 [a]11,7 157[q]3:1:Временной ряд квартальной динамики прибыли компании сглаживается с использованием экспоненциальной средней.
Найти сглаженное значение второго уровня, приняв параметр сглаживания 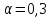 . Начальный параметр S0 принять равным средней арифметической первых трех уровней временного ряда.[a]10,97 [a]8,14 [a]11,43 [a]12,67 [a]10,15 158[q]3:1:Данные об объеме перевозок грузов указаны в таблице:
С помощью экспоненциальной средней найдите сглаженное значение второго уровня, приняв параметр сглаживания 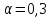. Начальный параметр S0 принять равным средней арифметической первых трех уровней временного ряда.[a]250 [a]260 [a]270 [a]265 [a]255 159[q]3:1:Данные об объеме перевозок грузов указаны в таблице:
С помощью экспоненциальной средней найдите сглаженное значение второго уровня, приняв параметр сглаживания |