АДПЭ. АДПЭ с циферками. aвременным рядом
 Скачать 303.21 Kb.
|
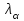 при 5% уровне значимости и количестве измерений временного ряда 10?[a]2 [a]1,8 [a]1,5 [a]1,2 [a]1,0 69[q]1:1:Расчетные значения критерия Ирвина определяются по формуле: [a] 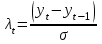 [a]  [a] 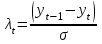 [a] 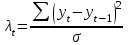 [a] 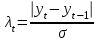 70[q]3:1:Используя критерий Ирвина, найти аномальные уровни временного ряда, заданного таблицей
[a]у2 [a]у4 [a]у5 [a]у7 [a]у1 71[q]1:1:Разность двух сравниваемых уровней, характеризующих величину изменения показателя за определенный промежуток времени, называется [a]абсолютным приростом [a]темпом роста [a]темпом прироста [a]коэффициентом ранговой корреляции [a]среднеквадратическое отклонение 72[q]1:1:При каких условиях правомерно использование среднего абсолютного прироста для получения прогнозной оценки показателя? [a]Близость динамики к развитию по показательной кривой [a]Близость динамики к развитию по экспоненциальной кривой [a]Близость динамики показателя к линейному развитию [a]Значительная вариация цепных абсолютных приростов [a]Незначительная вариация базисных абсолютных приростов 73[q]1:1: При каких условиях правомерно использование среднего темпа роста для получения прогнозной оценки показателя? [a]Близость динамики к развитию по показательной кривой [a]Близость динамики к развитию по гиперболической кривой [a]Близость динамики показателя к линейному развитию [a]Значительная вариация цепных абсолютных приростов [a]Незначительная вариация базисных абсолютных приростов 74[q]1:1:При каких условиях правомерно использование среднего темпа прироста для получения прогнозной оценки показателя? [a]Близость динамики к развитию по гиперболической кривой [a]Близость динамики показателя к линейному развитию [a]Значительная вариация цепных абсолютных приростов [a]Незначительная вариация базисных абсолютных приростов [a]Близость динамики к развитию по показательной кривой 75[q]1:1:В чем заключаются преимущества интуитивных методов прогнозирования? [a]возможность прогнозирования количественных изменений [a]принципиальная невозможность исключить полностью субъективизм в оценках экспертов [a]невозможность обеспечить абсолютно объективную оценку компетентности экспертов [a]возможность анализа и прогноза развития объекта, не имеющего предыстории [a]возможность прогнозирования сезонных изменений 76[q]2:1:Для модели с распределенным лагом 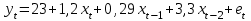 найдите долгосрочный мультипликатор.[a]0,29 [a]1,2 [a]1,49 [a]4,79 [a]3,3 77[q]2:1:Для модели с распределенным лагом 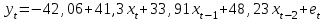 найдите промежуточный мультипликатор.[a]41,3 [a]33,91 [a]48,23 [a]75,21 [a]123,44 78[q]2:1:Для модели с распределенным лагом 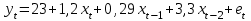найдите промежуточный мультипликатор.[a]0,29 [a]1,2 [a]1,49 [a]4,79 [a]3,3 79[q]2:1:Для модели с распределенным лагом найдите долгосрочный мультипликатор.[a]41,3 [a]33,91 [a]48,23 [a]75,21 [a]123,44 80[q]2:1:Для модели с распределенным лагом  найдите краткосрочный мультипликатор.[a]87,55 [a]120 [a]97,7 [a]207,55 [a]305,25 81[q]3:1:Для модели с распределенным лагом найдите средний лаг модели.[a]0,29 [a]0,39 [a]0,32 [a]1,03 [a]1,31 82[q]3:1:Для модели с распределенным лагом найдите средний лаг модели.[a]1,05 [a]0,27 [a]0,39 [a]0,78 [a]0,33 83[q]2:1:Зависимость объемов ВВП от инвестиций описывается моделью с распределенным лагом  . На сколько в среднем вырастет ВВП в текущем периоде с увеличением инвестиций на 1 усл. ед?[a]на 41,6 усл.ед [a]на 2,32 усл.ед [a]на 0,96 усл.ед [a]на 0,72 усл.ед [a]на 1,6 усл.ед 84[q]2:1:Зависимость объемов ВВП от инвестиций описывается моделью с распределенным лагом . На сколько в среднем вырастет ВВП через год с увеличением инвестиций на 1 усл. ед?[a]на 2,32 усл.ед [a]на 3,28 усл.ед [a]на 4 усл.ед [a]на 5,6 усл.ед [a]на 1,6 усл.ед 85[q]2:1:Зависимость объемов ВВП от инвестиций описывается моделью с распределенным лагом . На сколько в среднем вырастет ВВП через два года с увеличением инвестиций на 1 усл. ед?[a]на 2,32 усл.ед [a]на 3,28 усл.ед [a]на 4 усл.ед [a]на 5,6 усл.ед [a]на 1,6 усл.ед 86[q]2:1:Зависимость объемов ВВП от инвестиций описывается моделью с распределенным лагом . На сколько в среднем вырастет ВВП через три года с увеличением инвестиций на 1 усл. ед?[a]на 2,32 усл.ед [a]на 3,28 усл.ед [a]на 4 усл.ед [a]на 5,6 усл.ед [a]на 1,6 усл.ед 87[q]3:1:Количество студентов заочной формы обучения ВУЗа изменялось с примерно постоянным темпом роста в течении пяти лет. На начало первого года количество студентов составило 950 человек, на начало пятого года – 1436 человек. Требуется рассчитать прогноз количества студентов на начало 7-го года, используя средний темп роста. [a]1532,5 [a]1643,3 [a]1592,5 [a]1679 [a]1765,5 88[q]3:1:Количество студентов заочной формы обучения ВУЗа изменялось с примерно постоянным темпом роста в течении пяти лет. На начало первого года количество студентов составило 950 человек, на начало пятого года – 1436 человек. Требуется рассчитать прогноз количества студентов на начало 6-го года, используя средний темп роста. [a]1532,5 [a]1643,3 [a]1592,5 [a]1679 [a]1766,1 89[q]3:1:Количество студентов заочной формы обучения ВУЗа изменялось с примерно постоянным абсолютным приростом в течении пяти лет. На начало первого года количество студентов составило 950 человек, на начало пятого года – 1436 человек. Требуется рассчитать прогноз количества студентов на начало 7-го года, используя средний абсолютный прирост. [a]1532,5 [a]1643,3 [a]1592,5 [a]1679 [a]1766,1 90[q]2:1:Количество студентов заочной формы обучения ВУЗа изменялось с примерно постоянным абсолютным приростом в течении пяти лет. На начало первого года количество студентов составило 950 человек, на начало пятого года – 1436 человек. Требуется рассчитать прогноз количества студентов на начало 6-го года, используя средний абсолютный прирост. [a]1532,5 [a]1643,3 [a]1557,5 [a]1679 [a]1766,1 91[q]1:1:Представление уровней временного ряда yt (t=1,2,…,n)в виде  , где  - трендовая компонента,  -сезонная компонента,  - случайная компонента, соответствует модели:[a]мультипликативной [a]аддитивной [a]смешанного типа [a]адаптивной [a]параболической 92[q]1:1:Представление уровней временного ряда yt (t=1,2,…,n)в виде  , где - трендовая компонента,  - циклическая компонента, -сезонная компонента, - случайная компонента, соответствует модели:[a]мультипликативной [a]аддитивной [a]смешанного типа [a]адаптивной [a]параболической 93[q]1:1:Последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления, называется: [a]скользящей средней [a]темпами роста [a]темпами прироста [a]временным рядом [a]линией тренда 94[q]1:1:На основе годовых данных об изменении урожайности картофеля в регионе были оценены коэффициенты линейного тренда:  Согласно модели среднегодовой прирост урожайности составил:[a]176,6 ц/га [a]172,2 ц/га [a]167,8 ц/га [a]4,4 ц/га [a]4,8 ц/га 95[q]1:1:Представление уровней временного ряда yt (t=1,2,…,n)в виде  , где - трендовая компонента, - циклическая компонента, -сезонная компонента, - случайная компонента, соответствует модели:[a]мультипликативной [a]аддитивной [a]смешанного типа [a]адаптивной [a]параболической 96[q]1:1:Более гладкий временной ряд будет получен при использовании простой скользящей средней: [a]5-членной [a]7-членной [a]11-членной [a]3-членной [a]19-членной 97[q]1:1:При сглаживании временного ряда 11-членной скользящей средней теряются уровни: [a]первые и последние 5 [a]первые и последние 11 [a]только первые 5 [a]только первые 11 [a]только последние 11 98[q]1:1:Временной ряд урожайности сглаживается с помощью трехлетней скользящей средней.
Сглаженное значение третьего уровня равно: [a]19,5 [a]18,1 [a]20,3 [a]18,6 [a]19,0 99[q]1:1:При использовании скользящей средней были потеряны 2 уровня в начале и 2 уровня в конце временного ряда. Для сглаживания использовалась скользящая средняя: [a]9-членная [a]7-членная [a]11-членная [a]3-членная [a]5-членная 100[q]2:1:Временной ряд квартальной динамики прибыли компании сглаживается 5-членной скользящей средней.
Сглаженное значение третьего уровня равно: [a]15,0 [a]13,4 [a]12,9 [a]14,8 [a]15,5 101[q]1:1:При сглаживании временного ряда скользящей средней при длине интервала сглаживания |