Билеты по информатике. Билет понятие информации. Свойства информации. Информация и данные. 3
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
БИЛЕТ 3.Измерение информации. Единицы измерения количества информации.1.6. Измерение информации В качестве единицы информации Клод Шеннон (американский инженер и математик, основатель теории информации) предложил принять один бит. Бит (англ. binary digit; также игра слов: англ. bit – немного) – один двоичный разряд в двоичной системе счисления, одна из самых известных единиц измерения информации. В теории информации бит – количество информации, необходимое для различения двух равновероятных сообщений. В вычислительной технике битом называют наименьшую "порцию" памяти компьютера, необходимую для хранения одного из двух знаков "0" и "1", используемых для внутримашинного представления данных и команд. На практике чаще применяется более крупная единица – байт. Байт (англ. byte) – единица хранения и обработки цифровой информации, равная восьми битам. Более крупные производные единицы информации: 1 Килобайт (Кбайт), 1 Мегабайт (Мбайт), 1 Гигабайт (Гбайт), 1 Терабайт (Тбайт), 1 Петабайт (Пбайт), и т.д. 1 Кбайт = 2 10 байт =1024 байт, 1 Мбайт = 2 10 Кбайт = 1024 Кбайт, 1 Гбайт = 2 10 Мбайт = 1024 Мбайт. БИЛЕТ 4.Системы счисления. Разновидности систем счисления. Перевод чисел из одной системы счисления в другую.1.7. Системы счисления. Система счисления – совокупность приемов представления, обозначения натуральных чисел: В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Основание позиционной системы счисления – количество символов (цифр), используемых для изображения чисел в данной системе счисления. За основание системы можно принять любое натуральное число. Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами: для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток – нет тока, намагничен – не намагничен и т.п.), а не, например, с десятью, – как в десятичной; представление информации посредством только двух состояний надежно и помехоустойчиво; возможно применение аппарата булевой алгебры для выполнения логических преобразований информации; двоичная арифметика намного проще десятичной. Недостаток двоичной системы счисления: длинная запись числа. Разработаны восьмеричная и шестнадцатеричная системы. Восьмеричная система счисления имеет восемь цифр: 0 1 2 3 4 5 6 7. Шестнадцатеричная – шестнадцать, причем первые 10 цифр совпадают по написанию с цифрами десятичной системы счисления, а для обозначения оставшихся шести цифр применяются большие латинские буквы. 1.7.1.Преобразование чисел из одной системы счисления в другую. Так как десятичная система для нас удобна и привычна, все арифметические действия мы делаем в ней, и преобразование чисел из произвольной недесятичной (q=10) системы в десятичную удобно выполнять на основе разложения по степеням q, например: 111001112) = 1 х 27+ 1 х 26+ 1 х 25+ 0 х 24+ 0 х 23+ 1 х 22 + 1 х 21 + 1 х 20 = 128 + 64 + 32 + 4 + 2 + 1 = 23110, или 3478 = 3 х 82 + 4 х 81 + 7 х 80= 3 х 64 + 4 x 8 + 7 = 23110. Преобразование из десятичной в прочие системы счисления проводится с помощью правил последовательного умножения и деления. При этом целая и дробная части переводятся отдельно. Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q, записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q, и т.д., пока последнее полученное неполное частное не станет равным нулю. Для дробных чисел правило последовательного деления заменяется правилом последовательного умножения. БЫСТРЫЙ ПЕРЕВОД ОНЛАЙН : https://calculatori.ru/perevod-chisel.html или : https://binary2hex.ru/numberconverter.html  БИЛЕТ 5.Системы счисления, использующиеся в вычислительной технике. Перевод двоичных чисел в восьмеричную и шестнадцатеричную системы и обратно.Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами. Разработаны восьмеричная и шестнадцатеричная системы. А люди для удобства используют десятичную систему счисления. 1.7.2.Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему. БЫСТРЫЙ ПЕРЕВОД ОНЛАЙН : https://calculatori.ru/perevod-chisel.html или : https://binary2hex.ru/numberconverter.html Перевод чисел из этих систем счисления (16,8) в двоичную и наоборот, прост и основан на методах триад и тетрад. Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) для восьмеричных чисел или тетрадой (четверкой цифр) для шестнадцатеричных чисел. Перевод из двоичной системы в восьмеричную или шестнадцатеричную: чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. Если крайние триады (тетрады) оказались неполными, они дополняются нулями в целой части числа – слева, в дробной части (после запятой) – справа. 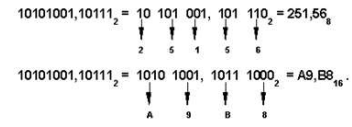 |
