теор вопросы. Ответы на теоретические вопросы. Быстрый переход Определение предела последовательности. Подпоследовательность. Частичный предел
 Скачать 2.1 Mb.
|
1 2 Схема исследования функции на выпуклость, вогнутостьНайти вторую производную функции. Найти точки, в которых вторая производная равна нулю или не существует. Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба. Пример Задание. Найти интервалы выпуклости/вогнутости функции  Решение. Найдем вторую производную заданной функции:  Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение :  Исследуем знак второй производной слева и справа от полученной точки: 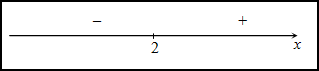 Так как на промежутке вторая производная , то на этом промежутке функция выпукла; в силу того, что на промежутке вторая производная - функция вогнута. Так как при переходе через точку вторая производная сменила знак, то эта точка является точкой перегиба графика функции. Ответ. Точка - точка перегиба графика функции. На промежутке функция выпукла, на промежутке функция вогнута. <Вернуться назад> 25. Асимптоты графика функции. Существование наклонной асимптоты. Виды асимптот:Определение Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений  или  равно или .Замечание. Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке . Поэтому вертикальные асимптоты следует искать в точках разрыва функции. Определение Прямая называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений  или  равно .Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую. Определение Прямая называется наклонной асимптотой графика функции , если  Нахождение наклонной асимптотыТеорема (условиях существования наклонной асимптоты) Если для функции существуют пределы  и  , то функция имеет наклонную асимптоту при .Замечание Горизонтальная асимптота является частным случаем наклонной при . Замечание Если при нахождении горизонтальной асимптоты получается, что  , то функция может иметь наклонную асимптоту.Замечание Кривая может пересекать свою асимптоту, причем неоднократно. Пример Задание. Найти асимптоты графика функции  Решение. Область определения функции:  а) вертикальные асимптоты: прямая - вертикальная асимптота, так как  б) горизонтальные асимптоты: находим предел функции на бесконечности:  то есть, горизонтальных асимптот нет. в) наклонные асимптоты :    Таким образом, наклонная асимптота: . Ответ. Вертикальная асимптота - прямая . Наклонная асимптота - прямая . <Вернуться назад> 26. Частные производные функции нескольких переменных. Теорема о равенстве смешанных производных.   Теорема 1(для функции двух переменных)Пусть функция f(x,y) определенна со своими частными производными fx,fy,fxy,fyx в некоторой окрестности точки (x0,y0), и при этом fxy и fyx непрерывны в этой точке. Тогда эти производные равны ( результат не зависит от порядка дифференцирования). fxy(x0,y0)=fyx(x0,y0) Теорема 2(обобщение)Если у функции n переменных смешанные частные производные m-го порядка непрерывны в некоторой точке, а производные низших порядков непрерывны в окрестности этой точки, то частные производные порядка m не зависят от порядка дифференцирования. <Вернуться назад> 27. Дифференцируемость функции нескольких переменных. Дифференциал. Обозначения: или – частная производная по «икс» или – частная производная по «игрек» Полный дифференциал первого порядка функции двух переменных имеет вид: И по неоднократным просьбам читателей, полный дифференциал второго порядка: Пусть функция дифференцируема в точке , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно и нелинейного членов:  где при . Определение Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается как или . Таким образом:  Замечание Дифференциал функции составляет основную часть ее приращения. Замечание Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента: Замечание Формулу для дифференциала функции можно записать в виде:  Отсюда получаем, что  Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента. Геометрический смысл дифференциалаДифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента . <Вернуться назад> 28. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума. Локальный экстремум функции двух переменных Необходимое условие локального экстремума дифференцируемой функции Если 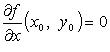 - точка экстремума функции f, то 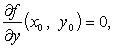и  или  Достаточные условия локального экстремума дважды дифференцируемой функции Обозначим 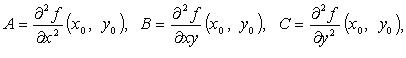 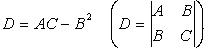 (Также принято обозначать: D-M1,2,3 ; A,B,C – Uxx, Uxy, …) Если D > 0, A > 0, то - точка минимума.Если D > 0, A < 0, то - точка максимума.Если D < 0, экстремума в точке нет.Если D = 0, необходимы дополнительные исследования. Пример от 3х переменных: Решение Найдем стационарные точки заданной функции, то есть точки, в которых выполняется необходимое условие существования экстремума. Для функции трех переменных стационарные точки (координаты точек) находятся из системы Для заданной функции , , и система примет вид Решениями системы являются и Получили две стационарные точки и . Для проверки достаточных условий экстремума в стационарной точке необходимо определить знаки определителей , и 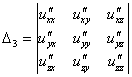 в этой точке.Найдем , , , , , . Для точки , , 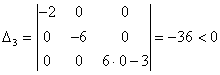 .Так как , , , то в точке функция имеет максимум, при этом . Для точки , , 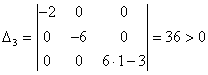 .Так как , , , то в точке функция не имеет экстремума. <Вернуться назад> Справка 1. Q: Как перейти по ссылке на определенный вопрос? A: Нажать на ссылку, потом - на появившуюся ссылку под ней:  Или “ctrl + ЛКМ”. 2. Q: Как добавить закладку? A: Выделить фрагмент текста, на который будет сделана закладка, нажать в верхнем меню “Вставка” -> “Закладка” 3. Q: Как добавить ссылку на закладку? A: Выделить текст будущей ссылки, нажать сочетание “ctrl + K”, кликнуть в появившеся меню “Закладки >” и выбрать нужную закладку. 4. Q: Как вставить разделитель после вопроса, чтобы следующий всегда был на новой странице? A: Нажать ctrl + Enter Спасибо! Всем, кто писал ответы на вопросы: Линар Саитов Арсений Автомонов Хитров Николай <Вернуться назад> By IKBO-08-16 & IKBO-13-17 2016-2018 ©mirea 1 2 |