Capp (ComputerAided Process Planning) Автоматизированное технологическая подготовка производства (планирование технологических процессов)
 Скачать 1.81 Mb.
|
|
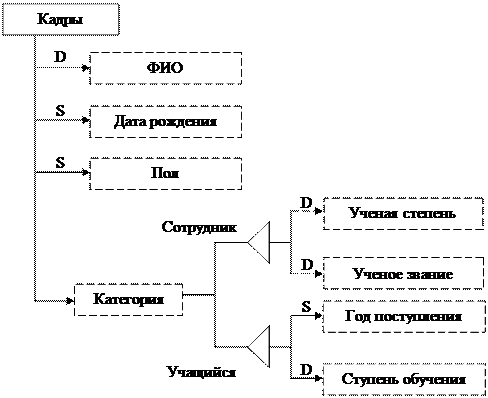
Составной объект соответствует отображению связи «целое - часть». Примеры таких объектов: класс – ученики, группа – студенты и т.п. Для отображения составных объектов в ИЛМ обычно не используются какие-либо специальные условные обозначения, а связь между составным и составляющими его объектами отображается так же, как это было описано выше (например, объекты Группа и Студенты связаны между собой отношением 1:М). Обобщенный объект отражает наличие связи «род - вид» между объектами предметной области. Например, объекты Студент, Школьник, Аспирант образуют обобщенный объект Учащиеся. Объекты, составляющие обобщенный объект, называются его категориями. Как «родовой» объект, так и «видовые» объекты могут обладать определенным набором свойств. Причем «видовые» объекты обладают всеми теми свойствами, которыми обладает «родовой» объект, плюс свойствами, присущими только объектам этого вида. Определение родо-видовых связей означает классификацию объектов предметной области по тем или иным признакам. Подклассы могут выделяться в ИЛМ в явном виде (рис. 3.5).
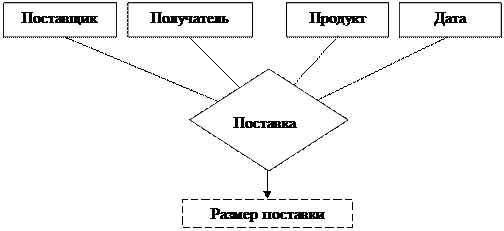
Рис. 3.5. Изображение обобщенного объекта На рис. 3.5 изображен фрагмент ИЛМ, отражающий обобщенный объект Кадры для высшего учебного заведения. Для обобщенного объекта выделено две категории: Сотрудник и Учащийся. Для обозначения подкласса в схеме использован треугольник. Естественно, что классификация может быть многоуровневой. В рассматриваемом примере подкласс Сотрудник, в свою очередь, может быть классифицирован на Преподаватель и Администрация; Учащийся на Студент и Аспирант. Агрегированный объект соответствует обычно какому-либо процессу, в который оказываются «вовлеченными» другие объекты. Например, агрегированный объект Поставка (рис. 3.6) объединяет в себе объекты Поставщик, Получатель, Продукт и Дата. Для отображения агрегированного объекта в схеме использован ромб. Агрегированный объект может так же, как и простой объект, иметь характеризующие его свойства. В рассматриваемом примере таким свойством является Размер поставки.
Рис. 3.6. Изображение агрегированного объекта Проектирование реляционных баз данных <567891011> Для реляционной БД проектирование логической структуры заключается в том, чтобы разбить всю информацию по таблицам, определив состав полей для каждой из этих таблиц. Для перехода от ИЛМ к реляционной можно воспользоваться следующими рекомендациями: 1) Для каждого простого объекта и его единичных свойств строится таблица, атрибутами которой являются идентификатор объекта и реквизиты, соответствующие каждому из единичных свойств:  2) Если у объекта имеются множественные свойства, то каждому из них ставится в соответствие отдельная таблица:  3) Если между объектом и его свойством имеется условная связь, то при отображении в реляционную модель возможны следующие варианты: · если многие из объектов обладают рассматриваемым свойством, то его можно хранить в БД так же, как и обычное свойство; · если только незначительное число объектов обладает указанным свойством, то при использовании предыдущего решения для многих записей в таблице значение соответствующего поля будет пустым. Для устранения этого недостатка выделяют отдельную таблицу, которая будет включать в себя идентификатор объекта и атрибут, соответствующий рассматриваемому свойству. 4) Если у объекта имеется составное свойство, то составляющие составного свойства либо помещаются в отдельные поля реляционной таблицы, либо в одно поле:  5) Если связь между объектами 1:1 и классы принадлежности обоих объектов являются обязательными, то для отображения данных объектов и связи между ними: · можно использовать одну таблицу, первичным ключом которой может быть идентификатор любого из двух объектов; · можно для каждого из этих объектов использовать отдельные таблицы, а связь между ними отразить, включив в одну из таблиц идентификатор связанного объекта из другой таблицы.  6) Если связь между объектами 1:1 и класс принадлежности одного объекта является обязательным, а другого – необязательным, то для каждого из этих объектов используют отдельные таблицы, а идентификатор объекта, для которого класс принадлежности является необязательным, добавляется в таблицу, соответствующую тому объекту, для которого класс принадлежности обязательный:  7) Если связь между объектами 1:1 и класс принадлежности каждого объекта является необязательным, то следует использовать три таблицы: по одной для каждого объекта и одну для отображения связи между ними: 8) Если между объектами предметной области имеется связь 1:М и класс принадлежности n – связного объекта является обязательным, то используют две таблицы: по одной для каждого объекта и в таблицу, соответствующую n – связному объекту, добавляется идентификатор 1 – связного объекта:  9) Если между объектами предметной области имеется связь 1:М и класс принадлежности n - связного объекта является необязательным, то создают три таблицы: по одной для каждого объекта и одну для отображения связи между ними:  10) Если между объектами предметной области имеется связь М:М, то для хранения такой информации потребуется три таблицы: по одной для каждого объекта и одна для отображения связи между ними (классы принадлежности могут быть: оба – обязательными, оба - необязательными, один – обязательный, другой – необязательный):  11) Агрегированному объекту, имеющему место в предметной области, в ДЛМ ставится в соответствие одна таблица, атрибутами которой являются идентификаторы всех объектов, «задействованных» в данном агрегированном объекте, а также реквизиты, соответствующие свойствам этого объекта:  Такое объединение информации в одну таблицу возможно только в том случае, если между объектами имеется связь 1:1. Если же между объектами имеется связь М:1 (или М:М), то выделяют по одной таблице для каждого объекта и одну таблицу для связи: R1 (ИО1, …) R2 (ИО2, …) R3 (ИО3, …) R4 (ИО1, ИО2, ИО3, С1). 12) При отображении обобщенных объектов могут быть приняты разные решения: · всему обобщенному объекту может быть поставлена в соответствие одна таблица:  · каждой из категорий ставится в соответствие отдельная таблица, то есть: R1 (ИО1, С1, С2, С4, С5) R2 (ИО1, С1, С2, С6, С7). Кроме этих двух «крайних» решений, возможны и комбинированные варианты. Выбор конкретного решения будет зависеть от многих факторов, в том числе от того насколько часто информация о разных категориях объекта обрабатывается совместно, как велико различие в «видовых» свойствах и др. 13) При отображении составного объекта также возможны разные решения: · если речь идет о составе изделий, то между «изделием» и «деталью» имеется связь типа М:М (одна деталь может входить в разные изделия и, наоборот, в изделие входят разные детали) – в этом случае для отображения связи «целое – часть» можно использовать три таблицы. В первой двух будет храниться информация о самих объектах, в третьей – информация о связи между ними и характере этой связи (для состава изделия это могут быть следующие поля: «что входит», «куда входит», «количество»); · если речь идет о составе какой-то организации, то между объектами скорее всего будет связь типа 1:М – в этом случае для отображения связи «целое – часть» можно использовать рекомендации пунктов 8 и 9. Реляционная модель БД, получаемая в результате использования предложенных рекомендаций, будет нормализованной и автоматически находиться в 4-й нормальной форме (вопросы нормализации рассматриваются в пятом разделе пособия).  Рис. 3.7. ER – модель предметной области Рассмотрим упрощенный пример предметной области, ER – модель которой изображена на рис. 3.7. Соответствующая ей даталогическая модель базы данных может иметь следующий вид: Факультет (Код_фак, Кр_наим_фак, Полн_наим_фак); Кафедра (Код_каф, Кр_наим_каф, Полн_наим_каф, Код_фак); Сотрудник (Таб_номер, ФИО, Дата_рождения, Пол, Код_каф, Должность, Уч_степень); Студент (Таб_номер, ФИО, Дата_рождения, Пол, Код_фак, Дата_поступления, Ступень_обучения); Ин_яз (Код_языка, наименование_языка); Знание_ин_яз (Таб_номер, Код_языка, Степень_владения); Дети (Таб_номер, Имя, Дата_рождения). Реляционная алгебра <6789101112> В основе реляционной модели лежит математическое понятие теоретико-множественного отношения. Теоретико-множественное отношение представляет собой подмножество декартова произведения доменов. Доменом называется набор значений элементов данных одного типа, отвечающий поставленным условиям (например, домен ФИО определяется на базовом типе строк символов, но в число его значений могут входить только те строки, которые могут изображать имя). Декартовымпроизведениемk доменов (D1, D2,…, Dk), (обозначается D1×D2×…×Dk), называется множество всех кортежей вида (V1, V2, …, Vk) длины k, таких, что V1∈D 1, V2∈D2, …, Vk∈Dk. Например, пусть D1 = {1, 2, 3}; D2 = {a, b, c, d} Тогда
или: D1×D2 = {(1,a), (1,b), (1,c), (1,d), (2,a), (2,b), (2,c), (2,d), (3,a), (3,b), (3,c), (3,d)} Отношением называют некоторое подмножество декартова произведения доменов (предполагаются только конечные отношения). Примеры отношений: 1) {(1,a), (1,c), (1,b)} - подмножество декартова произведения доменов D1×D2; 2) Ø. В реляционных СУБД для выполнения операций над отношениями используют две группы языков, имеющие в качестве своей математической основы теоретические языки запросов, предложенные Э. Коддом: · реляционную алгебру; · реляционное исчисление. Реляционнойалгеброй называют систему операций манипулирования отношениями, каждый оператор которой в качестве операнда имеет одно или более отношений и образует отношение по заранее обусловленному правилу. Вариант реляционной алгебры, предложенный Коддом, включает в себя следующие операции: объединение, разность, пересечение, декартово (прямое) произведение, выборка (селекция), проекция, деление и соединение. Упрощенное графическое представление перечисленных операций показано на рис. 4.1. 1) Объединением двух отношений (r ∪ s) является отношение, содержащее все кортежи, которые принадлежат либо r, либо s, либо им обоим. Данная операция применяется к отношениям с одной и той же схемой. Схемойотношенияr называется конечное множество имен атрибутов {A1, A2, …, An}. Примеры: a) Пусть k и m – отношения со схемой ABC:
Тогда объединение данных отношений:
б) Пусть отношение R1 – множество поставщиков из Москвы, а R2 – множество поставщиков, которые поставляют деталь D1: R1 R2
Тогда объединение данных отношений даст поставщиков из Москвы, либо поставщиков, которые поставляют деталь D1, либо тех и других: R1 ∪ R2
2) Разностью двух отношений (обозначается r - s) является отношение, содержащее все кортежи, которые принадлежат r, но не принадлежат s. Операция применяется к отношениям с одной и той же схемой. Примеры: а)
б) Разность отношений R1 и R2 даст поставщиков из Москвы, не поставляющих деталь D1: R1 – R2
3) Пересечением двух отношений (обозначается r ∩ s) является отношение, содержащее все кортежи, которые принадлежат одновременно r и s. Операция применяется к отношениям с одной и той же схемой. Примеры. а)
б) Пересечение отношений R1 и R2 даст всех поставщиков из Москвы, поставляющих деталь D1: R1 ∩ R2
  Рис. 4.1. Основные операции реляционной алгебры 4) Декартовымпроизведением отношения r степени k1 и отношения s степени k2 (r × s) является отношение степени (k1 + k2), содержащее такие кортежи, первые k1 элементов которых принадлежат r, а последние k2 элементов принадлежат s. Примеры: а) Даны отношения k и m
Тогда
б) Пусть отношение R1 – множество поставщиков, а S1 – множество деталей: R1 S1
Тогда декартово произведение данных отношений: R1 × S1
5) Выборка (применяется к одному отношению). Результатом ее применения к отношению r является другое отношение, представляющее собой подмножество кортежей отношения r с определенным значением в выделенном атрибуте. Пусть r отношение со схемой R, A – атрибут в R и a – элемент из домена А. Тогда  – операция выборки в r кортежей, в которых значение A равно a. В условии выборки можно использовать константы, логические операции и операции сравнения.Примеры: а) 
б) Дано отношение R1 R1
Тогда 
6) Проекция(применяется к одному отношению) - операция выбора подмножества столбцов. Пусть r – отношение со схемой R, Х – подмножество из R. Проекция r на X  есть отношение  , полученное вычеркиванием столбцов, соответствующих атрибутам в R – X, и исключением из оставшихся столбцов повторяющихся строк.Примеры. а) Пусть k - отношение со схемой АВС:
Тогда запись  означает, что из каждого кортежа, принадлежащего k, формируется кортеж длины 2 из третьего и первого его атрибутов в указанном порядке:
Записи эквивалентна запись  .б) Пусть S1 - отношение, содержащее информацию о деталях: S1
Тогда 
7) Деление. Пусть r – отношение со схемой R, s – отношение со схемой S и S ⊆ R. Положим  = R – S. Частное от деления r на s (r ÷ s) – это максимальное подмножество  множества  , такое, что декартово произведение и s содержится в r.Примеры: а) Даны отношения k и m
Тогда
б) Имеется отношение |
D1×D2 =