Цель работы изучение связи между видом свободного процесса в элек трической цепи и расположением ее собственных частот (корней характери стического уравнения) на комплексной плоскости
 Скачать 4.04 Mb. Скачать 4.04 Mb.
|
|
Цель работы: изучение связи между видом свободного процесса в элек- трической цепи и расположением ее собственных частот (корней характери- стического уравнения) на комплексной плоскости; экспериментальное опре- деление собственных частот и добротности RLC-контура по осциллограм- мам. Основные теоретические положения. Поведение линейных цепей описывается линейными дифференциаль- ными уравнениями; при этом вид свободного процесса определяется корнями pkхарактеристического уравнения (собственными частотами цепи). 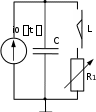 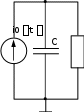 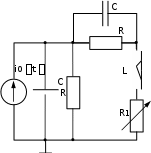 R Rа б в Рис. 3.1 При возбуждении цепи источником тока собственные частоты можно рассчитать как нули входной проводимости цепи нения Y p 0 . Y p, т. е. как корни урав- Для цепи первого порядка, представленной на рис. 3.1, а, 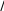 pC1 R, откуда pC1 R, откудаY p 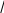 p1 1 RC. (3.1) p1 1 RC. (3.1)Для цепи второго порядка, изображенной на рис. 3.1, б, 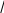 pC1 pL R1 , откуда pC1 pL R1 , откудаY p (3.2) Для цепи третьего порядка, представленной на рис. 3.1, в, откуда Y p pC 1 , 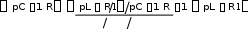 R R2 LC (3.3) Определение добротности Q RLC- контуров по виду свободного процесса. Для последовательного RLC-контура 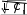  Q L L0 0 , (3.4) Q L L0 0 , (3.4)  R R 2 где 0 1 LC – частота незатухающих колебаний в идеальном контуре 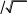 R R1 0. Согласно (3.2) собственные частоты последовательного RLC- контура можно записать следующим образом: R R1 0. Согласно (3.2) собственные частоты последовательного RLC- контура можно записать следующим образом:причем: Q < 0,5 соответствует апериодический режим; Q = 0,5 – критический режим; Q > 0,5 – колебательный режим; Q → ∞ – незатухающий колебательный режим; При Q> 10 с высокой степенью точности можно считать  p1,2 0 p1,2 0 2Q j0 . 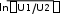 В этом случае формула, позволяющая определить добротность по ос- циллограмме схемы представленной на рис. 3.2, б, В этом случае формула, позволяющая определить добротность по ос- циллограмме схемы представленной на рис. 3.2, б, Q 0 Q 02 2  2T 2T . (3.10) Для повышения точности можно брать отношение напряжений за nпе- риодов колебаний. Тогда 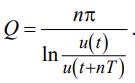 Обработка результатов
C = 0,02 мкФ, R = 5 кОм kр (коэффициент развертки)= 0,1 мс/дел kо (коэффициент отклонения)= 0,2 В/дел 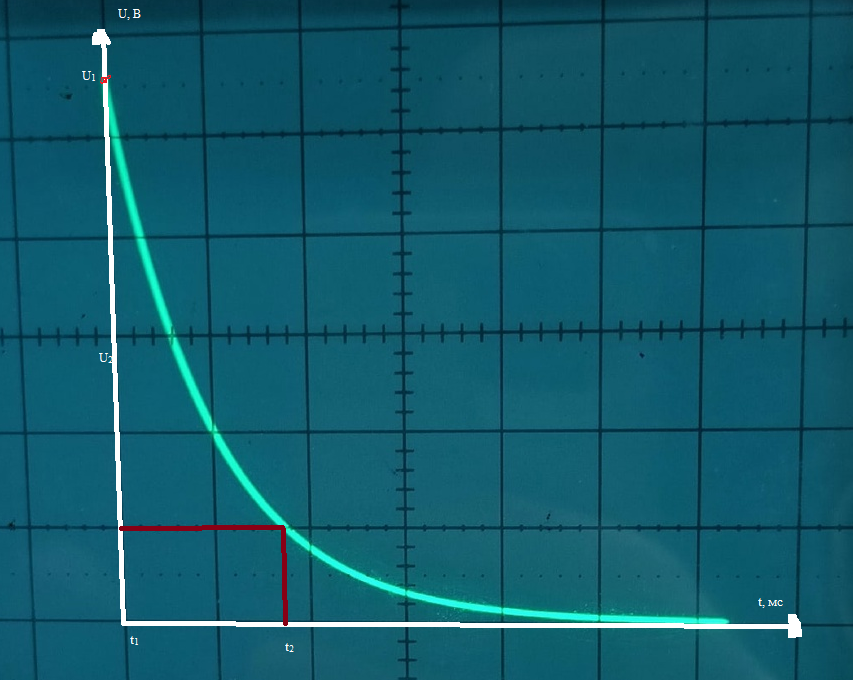 Рисунок 3.2 – Осциллограмма цепи первого порядка Рисунок 3.2 – Осциллограмма цепи первого порядкаРасчеты: Р  исунок 3.3 – Расчет собственной частоты цепи, диаграмма расположения собственной частоты исунок 3.3 – Расчет собственной частоты цепи, диаграмма расположения собственной частоты Вопросы: 1) Каким аналитическим выражением описывается осциллографируемый процесс? 2) Соответствует ли найденная собственная частота теоретическому расчету? Ответы: 1 (В нашем случае u(t)=A*e^(-9*103*t)) 2) Найденная собственная частота цепи не соответствует теоретическому расчету (погрешность измерения порядка 10%)
3.1, б. C = 0,02 мкФ, L = 25 мГн Колебательный режим: 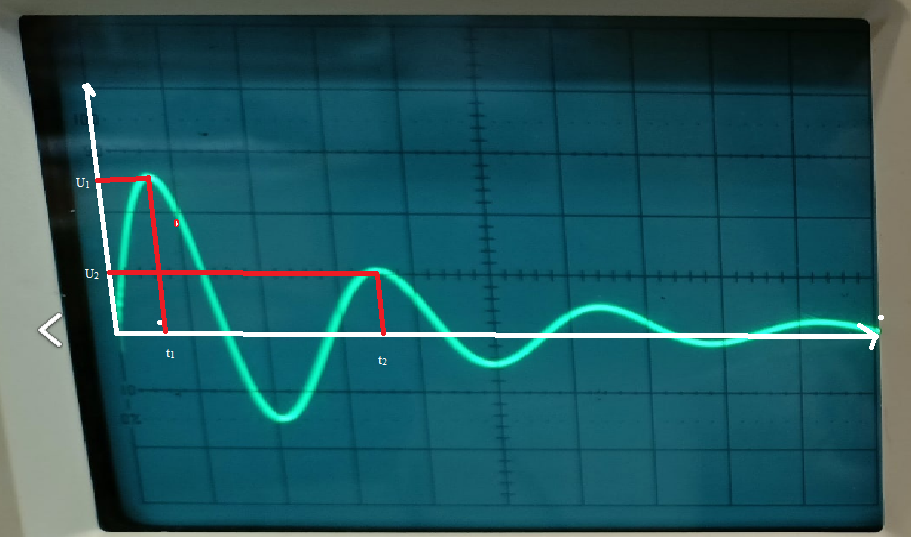 Рисунок 3.4 – Осциллограмма цепи второго порядка (колебательный режим) Расчеты:  Рисунок 3.5 - Расчет добротности и собственной частоты цепи 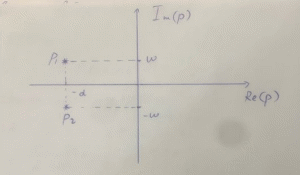 Рисунок 3.6 – Диаграмма расположения собственной частоты для цепи второго порядка в колебательном режиме Апериодический режим: 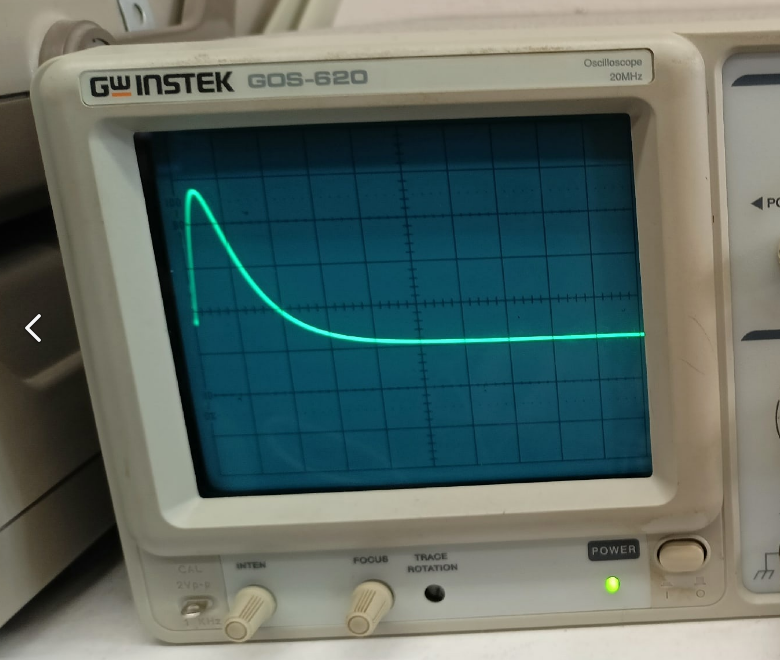 Рисунок 3.7 – Осциллограмма цепи второго порядка (апериодический режим)  Рисунок 3.8 - Расчет собственной частоты цепи, диаграмма расположения собственной частоты для цепи второго порядка в апериодическом режиме Рисунок 3.8 - Расчет собственной частоты цепи, диаграмма расположения собственной частоты для цепи второго порядка в апериодическом режимеКритический режим: R1=1,5 кОм 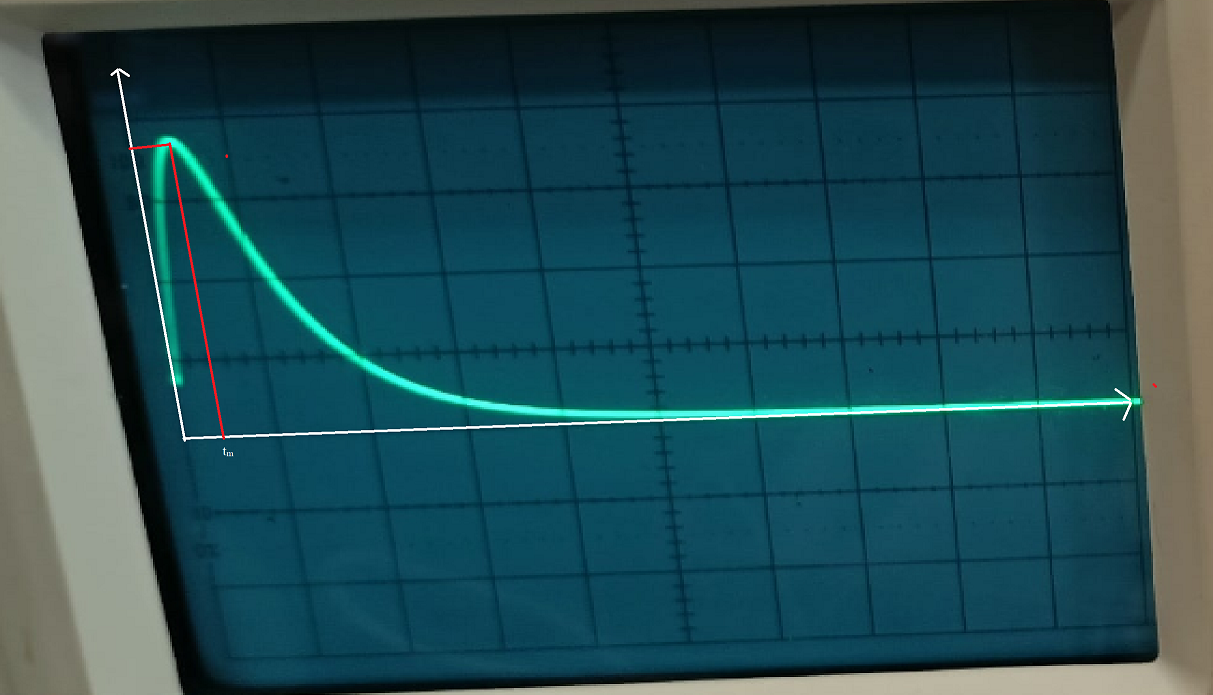 Рисунок 3.9 – Осциллограмма цепи второго порядка (критический режим) Расчеты:  Рисунок 3.10 - Расчет собственной частоты цепи, диаграмма расположения собственной частоты для цепи второго порядка в критическом режиме Незатухающий колебательный режим: R1= 0 Ом 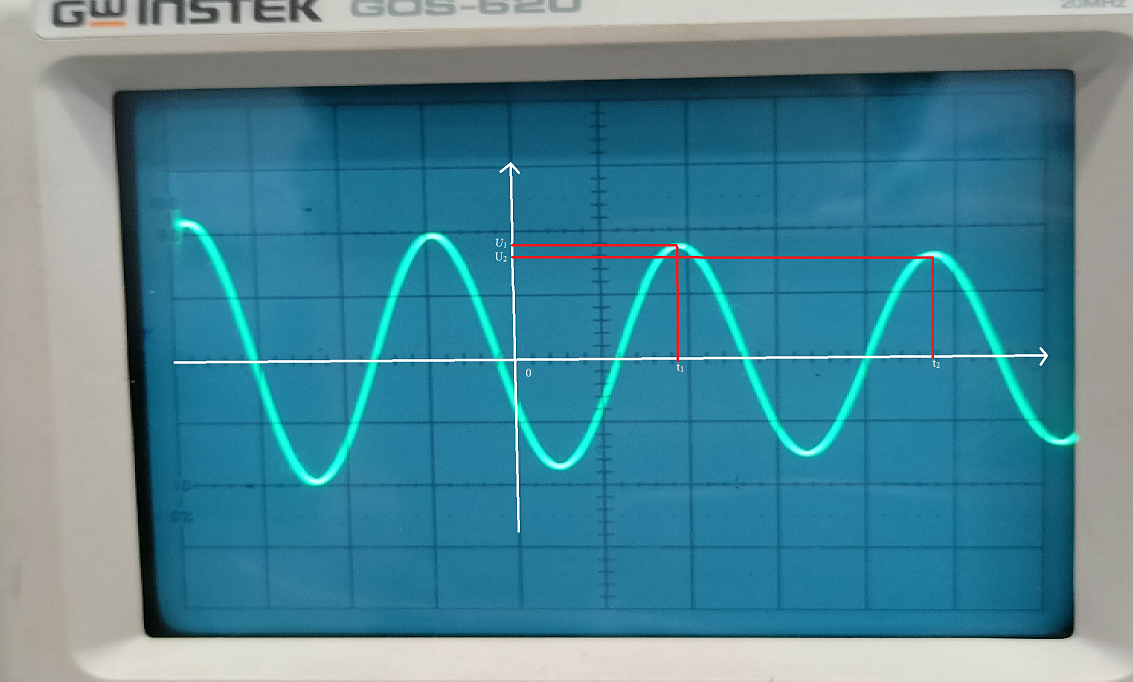 Рисунок 3.11 – Осциллограмма цепи второго порядка (незатухающий колебательный режим) Расчеты:  Рисунок 3.12 - Расчет добротности и собственной частоты цепи, диаграмма расположения собственной частоты для цепи второго порядка в незатухающем колебательном режиме Вопросы: Какими аналитическими выражениями (в общем виде) описываются процессы во всех четырех случаях? 4) Соответствуют ли найденные собственные частоты теоретическому расчету? 5) Каковы теоретические значения собственных частот при R1 3 кОм и соответствует ли этим значениям снятая осциллограмма? 6) Как соотносятся найденные значения добротности с результатами теоретического расчета? Ответы: 3) Процессы описываются следующими аналитическими выражениями: u(t) = A1cos(ω0t) + A2sin(ω0t) для колебательного незатухающего режима; Найденные собственные частоты не соответствуют теоретическому расчету в незатухающем и затухающем колебательных режимах, в критическом режиме вычисленная частота с учетом небольшой погрешности равна теоретическому значению. Теоретические значения собственных частот при R1 3 кОм равны -2*104 с-1 и -105 с-1. Осциллограмма соответствует найденным значениям, т.к. теоретическая зависимость соответствует экспериментальной (см. рис. 3.13 и рис 3.7). Оба графика затухают к 0.3 мс. Максимумы графиков приходятся на одно и тоже значение (примерно 0,02-0,03 мс) 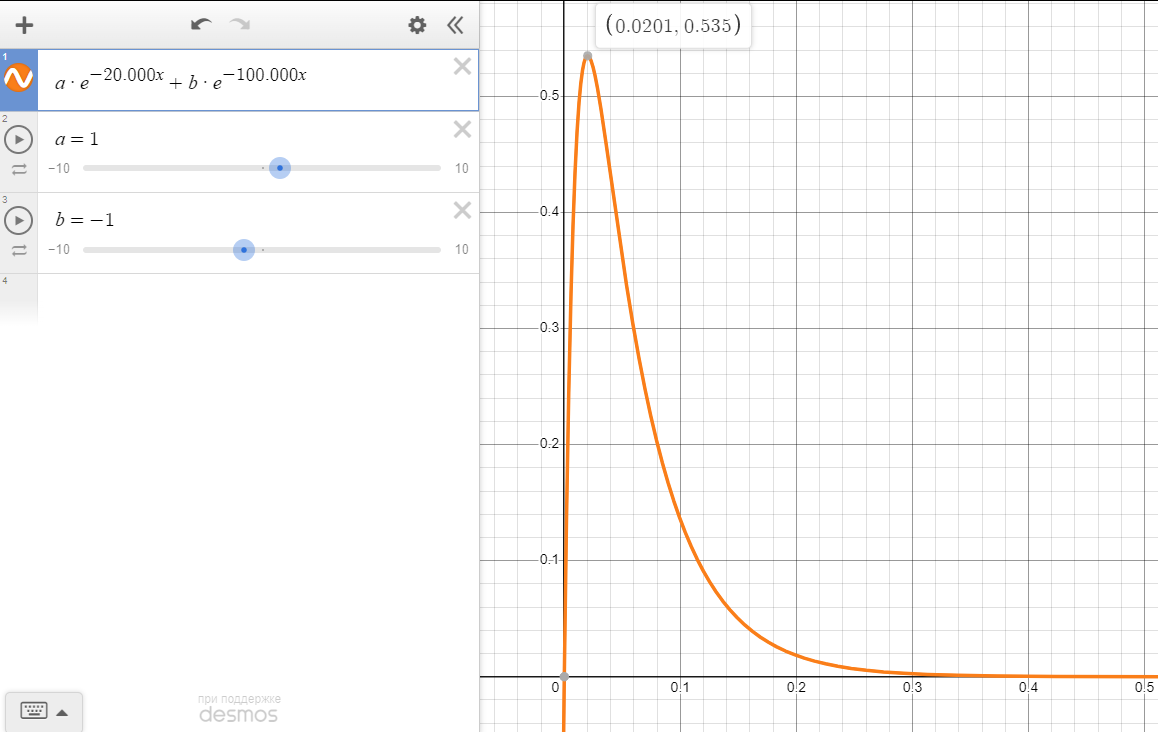 Рисунок 3.13 - График теоретической зависимости напряжения на резисторе от времени Вычисленные значения добротности отличаются от теоретических. Так, в колебательном затухающем режиме результаты отличаются примерно на 1, в незатухающем режиме (где добротность в теории стремится к бесконечности) значение равно 24
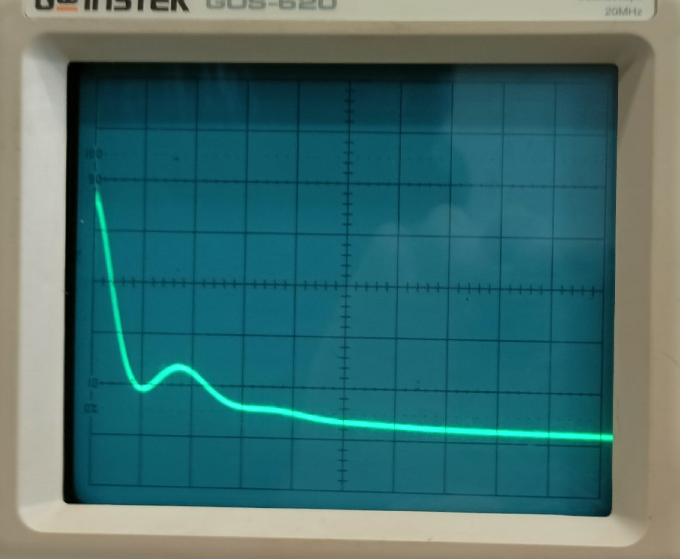 Рисунок 3.13 – Осциллограмма цепи третьего порядка Расчеты:  Рисунок 3.14 - Расчет собственных частот цепи, диаграмма расположения собственных частот для цепи третьего порядка Вопросы: Каким аналитическим выражением описывается осциллографируемый процесс? Каковы значения собственных частот, вычисленные согласно (3.3), и соответствует ли этим значениям снятая осциллограмма? Ответы: 7) Процесс в цепи третьего порядка описывается следующим аналитическим выражением: u(t) = A1e−α1t + A2e−α2tsin(ωt) + A3e−α2tcos(ωt) 8) Значения собственных частот рассчитаны на рис. 3.14. При сравнении двух графиков зависимостей (теоретической и экспериментальной) можно сделать вывод о том, что зависимости примерно одинаковы. 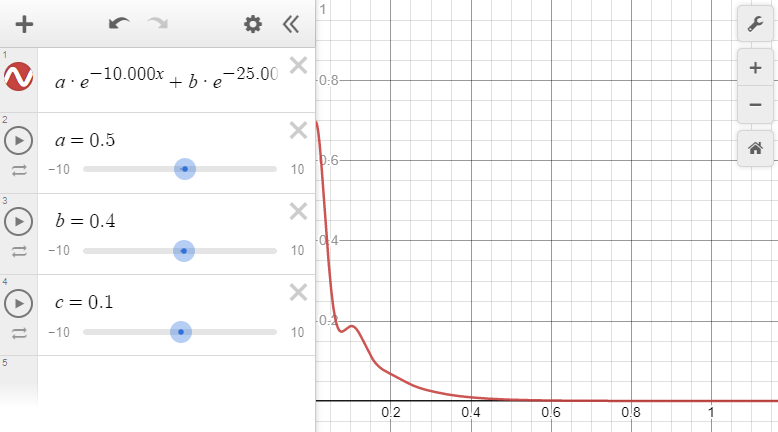 Рисунок 3.15. – Теоретическая зависимость входного напряжения от времени Значения параметров a,b,c (A1, A2, A3 соответственно) заданы произвольно с целью упрощения работы с графиком зависимости Выводы: В ходе лабораторной работы были исследованы и проанализированы различные режимы свободного процесса в цепях первого, второго и третьего порядков. Были получены теоретические и экспериментальные значения собственных частот цепи для режимов. Так, теоретическое значение частоты для цепи первого порядка равно р=10-4 с-1 , что, в свою очередь, с учетом малой погрешности совпадает с экспериментальным значением, полученным с помощью осциллограммы (р=9 * 10-3 с-1 ) Получены значения добротности, также были найдены значения собственных частот, которые, в свою очередь, сравнивались с результатами вычислений полученными с помощью осциллограмм. Различия в полученных данных может быть вызвано неточностью снятия показаний, наличием ненулевого сопротивления проводов и т.п. |
