10классматематика. Целые и рациональные числа
 Скачать 1.27 Mb.
|
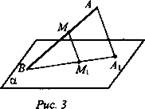
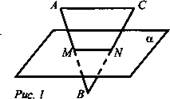
ΔMBN.Цели: 1) повторить аксиомы стереометрии и применение их при решении задач домашнего задания; 2) научить применять следствия из аксиом при решении задач, а также закрепить умение применять аксиомы стереометрии при решении задач; 3) формировать умения работать в группе. Ход урока: I. Организационный момент II. Изучение нового материала Рассмотрим и докажем следствия из аксиом. Два следствия есть в учебнике , их будут изучать первая и вторая группа. А потом докажут у доски. Третье следствие «Через две параллельные прямые можно провести плоскость и притом только одну» будет доказывать третья группа самостоятельно. Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна. Учащиеся записывают формулировку в тетради и, отвечая на вопросы учителя, делают соответствующие записи и рисунки в тетрадь. - Что дано в теореме? (прямая и не лежащая на ней точка) - Что надо доказать? (проходит плоскость; одна) - Что можно использовать для доказательства? (аксиомы стереометрии) - Какая из аксиом позволяет построить плоскость? (А1, через три точки проходит плоскость и притом только одна) - Что есть в данной теореме и чего не хватает для использования А1 (имеем – точку; необходимы – еще две точки) - Где построим еще две точки? (на данной прямой) - Какой вывод можем сделать? ( через три точки строим плоскость) - Принадлежит ли данной плоскости прямая? ( да) - На основании чего можно сделать такой вывод? ( на основании А2: если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости) - Сколько плоскостей можно провести через данные прямую и данную точку? (одну) - Почему? (так как плоскость, проходящая через прямую и плоскость, проходит через данную точку и две точки на прямой, значит по А1 эта плоскость – единственная) Теорема 2. Через две пересекающиеся прямые проходит плоскость и притом только одна. Учащиеся доказывают теорему самостоятельно, затем прослушиваются несколько доказательств и делаются дополнения и уточнения (если они необходимы) Обратить внимание на то, что доказательство опирается не на аксиомы, а на следствие 1. Теорема 3. Доказывает представитель от третьей группы учащихся. III. Закрепление изученного материала Учащиеся решают задачи № 7, 10, 14 из учебного пособия, делая соответствующие рисунки и записи на доске и в тетрадях. IV. Подведение итогов: - Сформулируйте аксиомы стереометрии. - Сформулируйте следствия из аксиом. Домашнее задание : п.3, №7 Математика 10 класс Дата ___________ Тема: Параллельные прямые в пространстве Цели: 1) Формирование знаний учащихся определения параллельных прямых в пространстве, теоремы о единственности прямой, параллельной данной, свойств параллельных прямых; 2) развитие аналитического мышления; формирование умений выделять главное и обобщать 3) развитие познавательного интереса к геометрии в пространстве. Ход урока: I. Организационный момент II. Изучение нового материала 1) Вспомним планиметрию. -Каким может быть взаимное расположение двух прямых на плоскости? (Совпадают, пересекаются, параллельны) -Какие прямые в планиметрии называются параллельными? -Перед вами модель куба -Что вы можете сказать о прямых АВ и CD? (Они лежат в одной плоскости, они не пересекаются, параллельны) - Являются ли параллельными прямые В1С и С1С, а AD1 и A1D? (нет, они лежат в одной плоскости, но пересекаются) -Что вы можете сказать о прямых B1C и A1D? Проблема. - Лежат ли они в одной плоскости? (Они лежат в одной плоскости, они параллельны) -Сделайте вывод, какие прямые в пространстве называются параллельными? -Вернёмся к модели куба -Что вы можете сказать о прямых ВС и АА1? (Они не лежат в одной плоскости, не пересекаются и не параллельны) Такие прямые называются скрещивающимися. Запись в тетрадь: «Две прямые называются скрещивающимися, если они не лежат в одной плоскости». 2) Являются ли параллельными следующие прямые? Ответ пояснить (слайды №10-11). 3) Делаем вывод о взаимном расположении прямых в пространстве (слайд №12). 4) Докажем теорему о параллельных прямых (слайды №13-14). 5) Учащиеся самостоятельно формулируют определение параллельных отрезков и лучей (слайд №15). III. Решение задач Решение у доски с комментариями. Задача № 17 (слайд №16). Дано: М - середина BD; N - середина CD; Q - середина АС; Р - середина АВ; AD = 12 см; ВС = 14 см. Найти: PMNQP - ? Решение: 1. MN || BC (по составу средней линии) ⇒ MN || PQ; PQ || BC. 2. РМ || AD (по составу средней линии) ⇒ PM || QN; NQ || DA. Значит, MNQP - параллелограмм (по определению) . 3. PQ = 7; РМ = 6 ⇒ PMNQP = 2(7 + 6) = 26 (см). Ответ: 26 см. IV. Подведение итогов урока. - Всегда ли две непересекающиеся прямые в пространстве параллельны? - Какие две прямые в пространстве называются параллельными? - Сколько можно провести в пространстве прямых, проходящих через любую точку пространства, параллельных данной прямой? Домашнее задание П. 4, теорема, задачи № 16, 18(а) Математика 10 класс Урок №16 Дата ___________ Тема: Параллельность трех прямых Цели: 1) Рассмотреть взаимное расположение двух прямых в пространстве, теорему о параллельности трех прямых, ввести понятие параллельных прямых в пространстве, сформировать умения применять полученных знания при решении задач. 2) Развивать память, логическое мышление, внимание, умение грамотно излагать собственные мысли, умение применять полученные знания. 3) Воспитывать аккуратность, старательность, ответственность, дисциплинированность, любовь к предмету Ход урока Организационный момент Актуализация опорных знаний учащихся 1. Какие прямые на плоскости называются параллельными? 2. Как называются углы, образованные при пересечении параллельных прямых секущей? Изучение нового материала Определение. Две прямые в пространстве называются параллельными, если они не пересекаются и лежат в одной плоскости. Используя рисунок, назовите параллельные прямые. Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. Задача 1. Вершина Q параллелограмма MNPQ лежит в плоскости α, а точки M, N, и P не лежат в этой плоскости. Докажите, что прямые NM и NP пересекают плоскость α. Доказательство. Прямая PQ пересекаетплоскость α в точке Q, так как Q ϵ α, поэтому, согласно лемме о пересечении плоскости параллельными прямыми, прямая NM, параллельная PQ, также пересекает плоскость α. Прямая MQ пересекает плоскость α в точке Q, поэтому параллельная ей прямая NP также пересекает плоскость α, что и требовалось доказать. Теорема. Если две прямые параллельны третьей прямой, то они параллельны. (рассмотреть доказательство теоремы в учебнике стр. 11) Решение задач Задача 1. Докажите, что если плоскость проходит через прямую, которая параллельна второй плоскости, и пересекает эту плоскость, то прямая пересечения параллельна данной прямой.  К доске вызывается ученик и доказывает задачу с наименьшей помощью со стороны учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение. Задача 2. Докажите, что если две плоскости пересекаются, параллельные одной и той же прямой, то прямая пересечения этих плоскостей параллельна данной прямой. .  Сначала рисунок к задаче и доказательство обсуждается с классом. Затем учащиеся записывают доказательство. После того, как задача решена, учитель показывает, как можно было записать доказательство. Решить № 26 Сторона АС треугольника АВС параллельна плоскости a , а стороны АВ и ВС пересекаются с этой плоскостью в точках М и N. Докажите, что треугольники АВС и МВN подобны. Слайд 11 Перед решением данной задачи необходимо вспомнить признаки подобия треугольников.  Доказательство 1. По утверждению 1° : МN || АC. Тогда угол А = углу ВМN (как односторонние при параллельных прямых). 2. угол В - общий. З. Таким образом, по двум углам треугольник АВС подобен треугольнику МВN. К доске вызывается ученик и доказывает задачу с помощью учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение. Слайд 12. Подведение итогов 1) Сформулируйте признак параллельности прямой и плоскости. 2) Сформулируйте утверждение, обратное признаки параллельности прямой и плоскости. Правильное ли оно? Домашнее задание № 27, № 30, № 31 Математика 10 класс Урок №17 Дата ___________ Тема: Параллельность прямой и плоскости Цели: 1) Ввести понятия параллельности прямой и плоскости; 2) Воспитывать аккуратность, старательность, ответственность, дисциплинированность, любовь к предмету 3) Сформировать представления учащихся об аксиомах стереометрии, взаимном расположении прямой и плоскости, плоскостей в пространстве, способах задания плоскости в пространстве. Ход урока Организационный момент Изучение нового материала Начать с рассмотрения взаимного расположения прямой и плоскости в пространстве В каком случае прямая и плоскость параллельны (рис. 1. а, б, в)? Прямая и плоскость называются параллельными, если они не имеют общих точек. 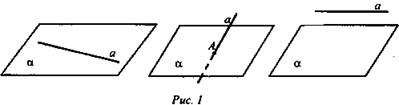 Показать на предметах обстановки классной комнаты прямые, параллельные плоскости пола. На модели куба (рис. 2) укажите плоскости, параллельные прямой DC, прямой DD1. 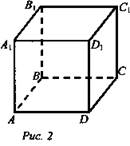 Как установить параллельность прямой и плоскости? Обратите внимание на модель куба. DC || (AA1B1). В плоскости (AA1B1) имеется прямая АВ || DC; DC || (A1B1C1). В плоскости (А1В1С1) имеется прямая D1C1 || DC. Сделайте предположение. Наличие в плоскости α прямой b || а является признаком, по которому можно сделать вывод о параллельности прямой а и плоскости α. Теорема: Дано: а, α; а ∉ α; b ∈ α; а || b (рис. 3). Доказать, что а || α. 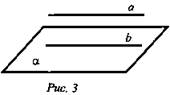 Доказательство: По условию b ∈ α; b || а.Предположим, что а ∩ α, тогда по лемме о пересечении плоскости параллельными прямыми прямая b ∩ α, но это невозможно, так как b ∈ α. Следовательно, а ∩ α, поэтому а || α и теорема доказана. Докажем два утверждения, которыми будем пользоваться при решении задач. 1. Если плоскость проходит через данную прямую, параллельную другой плоскости и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Дано:  (рис. 4)Доказать: а || b. 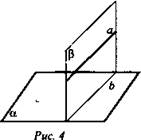 Доказательство: По условию  значит, а || b, так как  2. Если одна из 2-х параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. Дано: а || b; а; а || α (рис. 5). Доказать: 1) b || α. 2) b ∈ α. 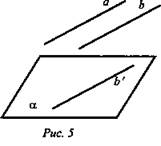 Доказательство: По условию а || b и α || а, следовательно, по лемме о пересечении плоскости параллельными прямыми  то есть b || α или b ∈ α.Решение задач № 18(б), № 20, 22 Подведение итогов Домашнее задание № 18 (a), 19, 21. Математика 10 класс Урок №18 Дата ___________ Тема: Параллельность прямой и плоскости Цели: 1) Закрепить и углубить знания и умения применять теоремы о параллельности прямых, прямой и плоскости при решении задач; подготовить учащихся к контрольной работе и зачету по данной теме. 2) Развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание; 3) Воспитывать у учащихся ответственное отношение к учебному труду, волю; Ход урока Организационный момент Устная работа. 1. Верна ли формулировка признака параллельности прямой и плоскости: «Прямая, параллельная какой-либо прямой на плоскости, параллельна и самой плоскости». (Нет, прямая может лежать в плоскости). 2. Прямые а и b параллельны. Какое положение может занимать прямая а относительно плоскости, проходящей через прямую b? 3. Даны прямая и две пересекающихся плоскости. Охарактеризовать все возможные случаи их взаимного расположения. Решение задач по теме урока. Задача № 22 Дано: A ∈ α, В ∈ α, С ∈ α; AM = МС; BN = NC. Доказать: MN || α. Доказательство: MN || АВ (по свойству средней линии), АВ ∈ α; MN || α по признаку. Перед решением задачи № 26 дать понятие отрезка, параллельного плоскости. «Отрезок параллелен плоскости, если прямая, содержащая этот отрезок, параллельна плоскости». Задача № 26 Дано: АС || α, АВ ∩ α = М; СВ ∩ α = N (рис. 1). Доказать: ΔАВС |
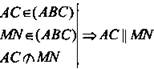(по определению).
АА1 = 5 см, ВВ1 = 7 см (рис. 2).
по лемме АА1 ∩ β. Получили противоречие, значит, С1 ∈ А1В1.
(Ответ: 6 см.)
(рис. 3).
Предположим, М1 ∈ А1В, тогда 
значит, 
что противоречит условию.
(Ответ: 12 см.)