Тема: Параллельные плоскости
Цели:
1) Рассмотреть свойства параллельных плоскостей;
2) Сформировать навык применения изученных свойств параллельных плоскостей при решении задач.
3) Средствами урока воспитывать у учащихся ответственное отношение к учебному труду, волевые качества личности, умение работать в коллективе.
Ход урока
Организационный момент
Актуализация опорных знаний учащихся
Теоретический опрос
а) Один ученик готовит у доски доказательство признака параллельно сти двух плоскостей. б) Д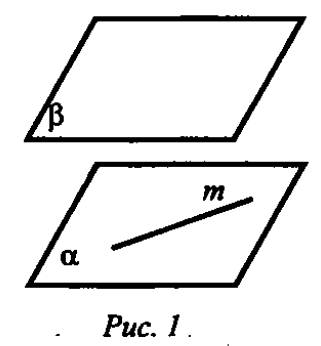 ругой записывает на доске решение до машней задачи № 55. в) Двое учащихся решают по карточкам ин- диивидуального опроса. 1. Плоскости а и р параллельны, прямая т параллельна плоскости р. ругой записывает на доске решение до машней задачи № 55. в) Двое учащихся решают по карточкам ин- диивидуального опроса. 1. Плоскости а и р параллельны, прямая т параллельна плоскости р.
Дано\ а || р, т с: а (рис. 1).
Доказать', что т || р.
Решение’.
1) Пусть т не параллельна р. т п р = К, К € р.
. к^р
2) £ е а Получили противоречие условию а || р. Сле- => а п р . дО вательнО 5 т у р цт о и требовалось доказать. т.к. т е а
2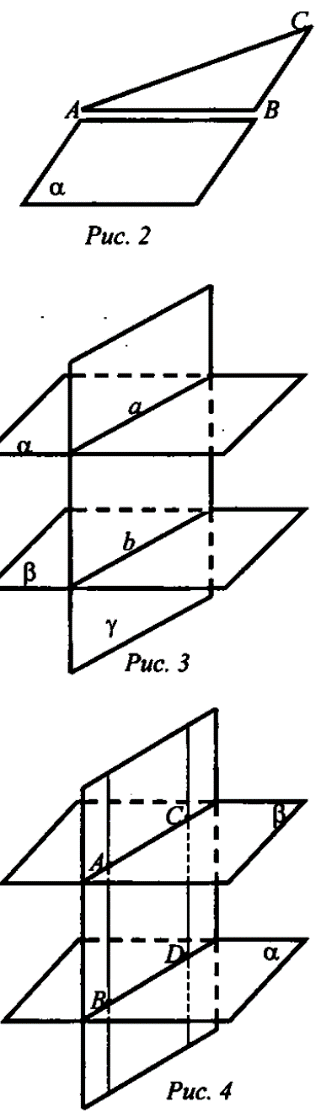 . Две стороны треугольника параллельны плоскости а. Докажите, что и третья сторона параллельна плоскости а. . Две стороны треугольника параллельны плоскости а. Докажите, что и третья сторона параллельна плоскости а.
Дано’. &АВС, АВ || а, ВС || а. (рис. 2).
Доказать’. АС || а.
Решение'. Если две пересекающиеся прямые плоскости АВС параллельны плоскости а, то (АВС) || а. Так как AC cz (АВС), а (АВС) || а, то АС || а. Что и требовалось доказать.
г) Фронтальный теоретический опрос
- сформулируйте определение параллельных плоскостей; - укажите модели параллельных плоскостей на предметах классной обстановки; - сформулируйте признак параллельности плоскостей.
Выслушивается доказательство теоремы и решение задачи № 55.
Изучение нового материала
1. Рассмотреть свойства параллельных плос костей. 1. Дано: а || р, у п а = а, у п р = b (рис. 3).
Доказать: а || Ь.
Доказательство: Предположим, что а п Ь.
Тогда а и р имели бы общую точку, что невоз можно, так как а || р по условию. Итак, а и b лежат в одной плоскости у и не пересекаются.
Значит, а || Ь. Свойство доказано.
2. Дано'. АВ || CD, а || р (рис. 4).
Доказать'. АВ = CD.
Доказательство:
71
у п а .у п р а|1Р => по свойству 1° АС || BD.
2) В четырехугольнике ABCD
AC\\BD
AB\\CD
=> ABCD- параллелограмм
В параллелограмме противоположные сто роны равны. Значит, АВ = CD. Что и требова лось доказать.
Закрепление изученного материала
1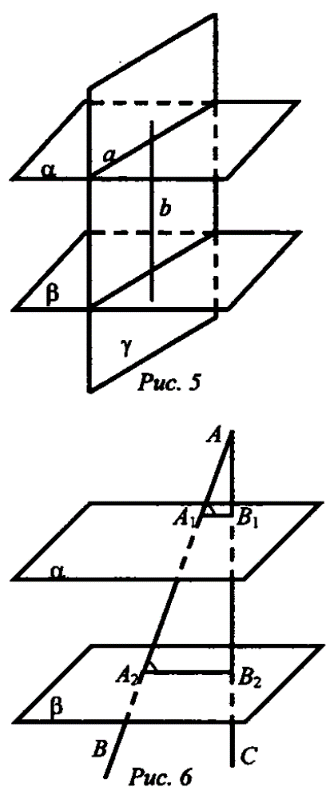 . Решение задачи 58 . Решение задачи 58
Дано: а || р, а пересекается с у (рис. 5).
Доказать, что р пересекается с у.
Решение: Пусть у пересекает а по прямой а.
Проведем в плоскости у прямую Ь, пересекаю щую а. Прямая b пересекает а, поэтому она пересекает параллельную ей плоскость р (зада ча № 55). Следовательно, и плоскость у, в кото рой лежит прямая Ь, пересекает плоскость р.
2. Задача 636 Дано: а ||р , /ВАС. ar>AB=Alt рг^А В А 2,
а п АС=Вь р n АС=В2, А\В\ = 18 см, ААi = 24 см, 3
АА2 - — А\А2 (рис. 6).
Найти: А2В2, АА2.
Решение: 1. (ВАС)су<1=А\В\, (ВАС) п р = А2В2. Так
как а || р, по свойству 1° параллельных плоскостей А \В\ || А2В2. 2. В (ВАС) ДА1АВ
4А2АВ2 (по двум углам: /А — общий, = /А А 2В2 как соот- ветственные при параллельных прямых AjBi и А2В2 и секущей АВ). Из подобия треугольников следует, что
=
АА2=АА1+А,А2 = 24 + А}А2,24+А1А2= 1 а ,А2, — А,А2 = АА, А,В, 2 2
A D
= 24, А ,А2 = 24 • 2 = 48 (см); АА2 = 48 + 24 = 72 (см); , „ 7218 с л , х
А2В2 =
24
= 54 СМ '
(Ответ: 54 см = А2В2, АА2 = 72 см.)
Самостоятельная работа
(см. приложение)
Подведение итогов
Домашнее задание
П. 11 № 59, 63а, 64.
Математика 10 класс Урок №25 Дата ___________
Тема: Тетраэдр
Цели:
1) Повторит понятие многоугольника в планиметрии
2) Ввести понятие тетраэдра;
3) Рассмотреть задачи, связанные с тетраэдром.
Ход урока
Организационный момент
Актуализация опорных знаний учащихся
I) Один ученик записывает на доске решение домашней задачи № 63 а.
Д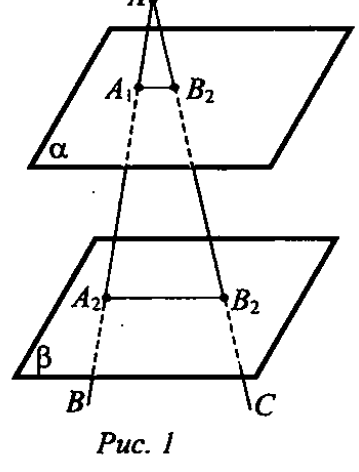 ано', а || р, ЛАВС,А} = а n АВ, А2 = р п АВ, Bi = а п АС, В2 ано', а || р, ЛАВС,А} = а n АВ, А2 = р п АВ, Bi = а п АС, В2
Р п АС;
AjA2 = 2AiAt AjA2 = 12 см, ABi = 5 см. (рис. 1).
Найти: АА2, АВ2.
Решение:
1. AiBi ЦА2В2 (по свойству 1° параллельных плоскостей).
2. ЛА2АВ2 ооЛА7АВу, = АА2 АВ2
3. Так как А/А2 = 2 AjA и А {А2 = 12 см, то А}А = 1 2 :2 = 6 см. 4. АА2 = 12 + 6 = 18 см. 5.
АХА АВХ 6 _ 5
АА2 АВ2 18 АВ2
АВ2 =15 см.
(Ответ: АА2 = 18см, АВ2 = 15 см.) 2) Двое решают по карточкам индивидуального опроса.
I. Отрезки АВ, АС и AD не лежат в одной плоскости. Точки К, M a N - соответственно их середины. а) Докажите, что плоскости BCD и KMN параллельны. б) Найдите площадь &ВСД, если = 36 м2.
(Ответ: SBcd = 144 м2.)
II. Три прямые, проходящие через точку М и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках А }, В и С, а вторую - в точках Л/, В} и Ch
а) Докажите, что ABC
&A}B]Ci.
б) Найти , если МС = СС/.
4В,
(Ответ: -j.)
3) Остальные отвечают на вопросы (устно).
1) Каково взаимное расположение двух плоскостей, если третья плоскость пересекает их по прямым: а) имеющим общую точ ку; б) не имеющим общих точек?
2) Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть ее боковыми сторонами?
3) Каким может быть взаимное расположение двух прямых, если эти прямые пересекают две параллельные плоскости, и их от резки, заключенные между плоскостями, не равны?
4) Две плоскости пересечены двумя параллельными прямыми. Выясните взаимное расположение этих плоскостей, если отрезки данных прямых, заключенные между этими плоскостями, не равны.
5) Прямая а пересекает параллельные плоскости а и р в точках А и В. Прямая Ь, параллельная прямой а, пересекает плоскости в точках D и С. Найдите периметр четырехугольника ABCD, если АВ = 3 см, ВС = 4 см.
6) Плоскости а и р параллельны, прямая т лежит в плоскости а.
Докажите, что прямая т параллельна плоскости р.
Изучение нового материала
И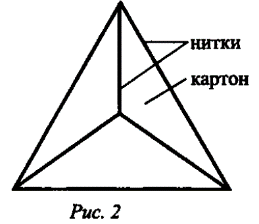 спользовать модели нескольких тетраэдров, а также гибкую модель из картона и ниток (рис. 2). спользовать модели нескольких тетраэдров, а также гибкую модель из картона и ниток (рис. 2).
1) Одна из глав нашего курса будет посвящена многогранникам - поверхностям геометрических тел, составленных из многоугольников. Познакомимся с одним из них сегодня на уроке - тетраэдром. Это даст нам возмож ность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоско стей на примере геометрических тел.
Вспомним, прежде всего, что мы понимали под многоугольником в планиметрии. (Ответы).
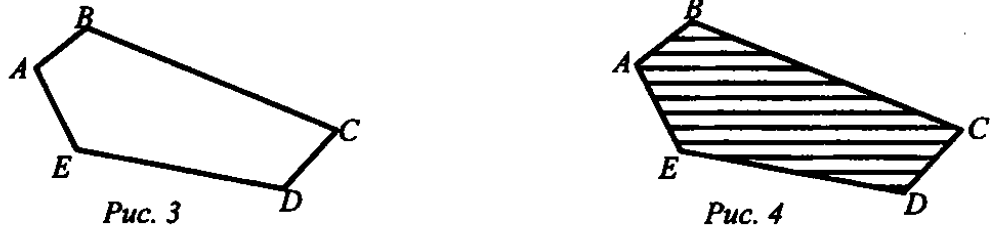
Учитель обобщает ответы учащихся: многоугольник мы рассматривали
либо как замкнутую линию без самопересечений, составленную из отрез
ков (рис. 3), либо как часть плоскости, ограниченную этой линией, вклю чая ее саму (рис. 4).
При рассмотрении поверхностей и тел в пространстве будем пользоваться вторым толкованием многоугольника.
При таком толковании любой много угольник в пространстве представляет собой плоскую поверхность.
2) Определение тетраэдра. Построим ДЛВС; точка D, не лежащая в плоскости этого треугольника. Соединив точку D отрезками с вершинами АЛ ВС, получим ADAB, &DBC, &DCA, получим тетраэдр.
И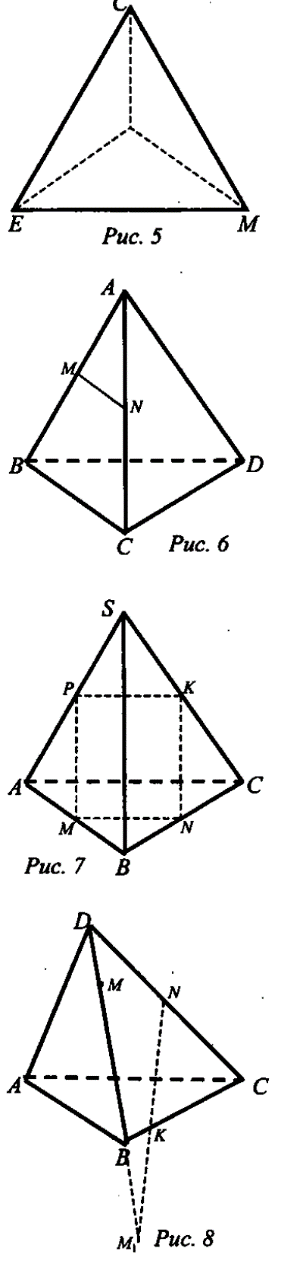 так, поверхность, составленная из четырех треугольников ДАВС, ДРАВ, &DBC и ДЛСА, на зывается тетраэдром и обозначается: DABC. так, поверхность, составленная из четырех треугольников ДАВС, ДРАВ, &DBC и ДЛСА, на зывается тетраэдром и обозначается: DABC.
Тетраэдр, то есть четырехгранник («тетра» - че тыре, «эдр» - грань). (Показ моделей тетраэдров.) 3) Треугольники, из которых состоит тетраэдр, называются гранями, их стороны - ребрами, а вер
шины - вершинами тетраэдра. Тетраэдр имеет
четыре грани, шесть ребер и четыре вершины.
Два ребра тетраэдра, не имеющие общих вер шин, называются противоположными.
На рис. 34
учебника AD и ВС, BD и AC, CD и АВ.
Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие - боковы
ми гранями. 4) Изображение тетраэдра на плоскости
(рис. 5).
Закрепление изученного материала
1) №68 (устно) по готовому чертежу (рис. 6).
2) №69. Дано'. SABC - тетраэдр, МА = МВ, BN=NC, М е а, N е а, ВС || а, а n (ABS) = РМ, ar\(BC S) = KN(pиc. 7).
Доказать'. РМЦ KN.
BS а (BCS)
В5|| а, (B C S n a = O f ) свойству 1°).
BS cz (ABS) ВВЦ а, (A B Sna = PM)
свойству 1°).
BS || KN, BS || РМ, KN || РМ (по теореме о
параллельности трех прямых).
3) № 716. Дано'. DABC - тетраэдр, М е DB, N<= DC, К е ВС (рис. 8).
Построить’, точку М\.
Условие’.
MX=KN r\{FBD).
1. =>BS\\KM (по
Решение:
1. NK^(DBC),DB<^(DBC).
2. NK не может быть параллельна прямой DB. Так как NK || (ADB) (по признаку) - это противоречит условию NK n DB.
3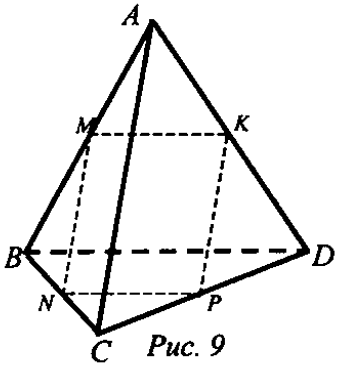 . DB cz (ADB), то NK n (ADB) = Mi. . DB cz (ADB), то NK n (ADB) = Mi.
4) Ns 73. Дано\ DABC - тетраэдр, М^АВ, N&BC, Л \ Ре CD, K eA D ; МА=МВ, NB=NC, PC = PD,
/ \ AC = 10 см, BD = 12 см, АК = KD (рис. 9).
Доказать*. К е. (MNPНайти'. Pmnpk-
Решение'.
(MNP) n (ABC) = MN, MN - средняя линия
M BC => MN || AC.
Q Puc. 9 '
2. MN\\(ACD) (по признаку параллельности прямой и плоскости), MN проходит через (MNP), (MNP) || (ACD).
Значит, линия пересечения (MNP) и (A CD) параллельна MN. 3. Пусть эта линия пересекается с ребром AD в точке К. Так как РК || MN и MN || АС, то РК || АС, а так как Р - середина AD, то РК - средняя линия ДЛС£>, то есть К - середина AD.
4. MN= КР=^АС = 5 см; NP= M K=^BD = 6 cm; Р = 2- (5 + 6) = 22см.
(Ответ: 22 см.)
Подведение итогов
Домашнее задание
П. 12,1 уровень: № 67(a), 70; II уровень: № 67, 71(a).
Математика 10 класс Урок №25 Дата ___________
Тема: Тетраэдр
Цели:
1) Cформировать представление о геометрическом теле – тетраэдре;
2) Gознакомить учащихся с основными элементами и способами заданий тетраэдра, а также его использование при решении задач;
3)
Ход урока
Организационный момент
Актуализация опорных знаний учащихся
Изучение нового материала
Использовать модели нескольких тетраэдров, а также гибкую модель из картона и ниток (рис.
1) Одна из глав нашего курса будет посвящена многогранникам - поверхностям геометрических тел, составленных из многоугольников. Познакомимся с одним из них сегодня на уроке - тетраэдром. Это даст нам возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей на примере геометрических тел.
Вспомним, прежде всего, что мы понимали под многоугольником в планиметрии. (Ответы).
Учитель обобщает ответы учащихся: многоугольник мы рассматривали либо как замкнутую линию без самопересечений, составленную из отрезков (рис. 3), либо как часть плоскости, ограниченную этой линией, включая ее саму (рис. 4).
При рассмотрении поверхностей и тел в пространстве будем пользоваться вторым толкованием многоугольника. При. таком толковании любой многоугольник в пространстве представляет собой плоскую поверхность.
2) Определение тетраэдра. Построим ΔАВС; точка D, не лежащая в плоскости этого треугольника. Соединив точку D отрезками с вершинами ΔABC, получим ΔDAB, ΔDBC, ΔDCA, получим тетраэдр.
Итак, поверхность, составленная из четырех треугольников ΔABC, ΔDAB, ΔDBC и ΔDCA, называется тетраэдром и обозначается: DABC.
Тетраэдр, то есть четырехгранник («тетра» - четыре, «эдр» - грань). (Показ моделей тетраэдров.)
3) Треугольники, из которых состоит тетраэдр, называются гранями, их стороны - ребрами, а вершины - вершинами тетраэдра. Тетраэдр имеет четыре грани, шесть ребер и четыре вершины.
Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. На рис. 34 учебника AD и ВС, BD и АС, CD и АВ.
Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие - боковыми гранями.
4) Изображение тетраэдра на плоскости (рис. 5).
Закрепление изученного материала
1) № 68 (устно) по готовому чертежу (рис. 6).
2) № 69. Дано: SABC - тетраэдр, МА = MB, BN = NC, 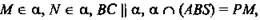 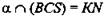 (рис. 7). (рис. 7).
Доказать: PM|| KN.
1. 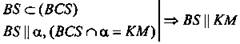 (по свойству 1°). (по свойству 1°).
2. 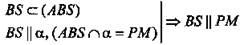 (по свойству 1°). (по свойству 1°).
3. BS || KN, BS || PM, KN || РМ (по теореме о параллельности трех прямых).
3) № 716. Дано: DABC - тетраэдр, M ∈ DB, N ∈ DC, К ∈ ВС (рис. 8).
Построить: точку М1.
Условие: M1 = KN ∩ (FBD).
Решение:
1. NK ⊂ (DBC), DB ⊂ (DBC).
2. NK не может быть параллельна прямой DB. Так как NK || (ADB) (по признаку) - это противоречит условию ⇒ NK ∩ DB.
3. DB ⊂ (ADB), то NK ⊂ (ADB) = М1.
4) № 73. Дано: DABC — тетраэдр, М ∈ АВ, N ∈ BC, Р ∈ CD, K ∈ AD; МА = MB, NB = NC, PC = PD, AC = 10 см, BD = 12 см, AK = KD (рис. 9).
Доказать: К ∈ (MNP).
Найти: PMNPK.
Решение:
1. (MNP) ∩ (ABC) = MN, MN - средняя линия ΔABC ⇒ MN || AC.
2. MN || (ACD) (по признаку параллельности прямой и плоскости), MN проходит через (MNP), (MNP) || (ACD). Значит, линия пересечения (MNP) и (ACD) параллельна MN.
3. Пусть эта линия пересекается с ребром AD в точке К. Так как РК || MN и MN || АС, то РК || АС, а так как Р - середина AD, то РК - средняя линия ΔACD, то есть К - середина AD.
4. 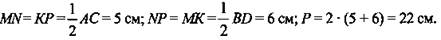 (Ответ: 22 см.) (Ответ: 22 см.)
Подведение итогов
Домашнее задание
П. 12, I уровень: № 67 (a), 70; II уровень: № 67, 71 (a).
|
 Скачать 1.27 Mb.
Скачать 1.27 Mb. ругой записывает на доске решение до машней задачи № 55. в) Двое учащихся решают по карточкам ин- диивидуального опроса. 1. Плоскости а и р параллельны, прямая т параллельна плоскости р.
ругой записывает на доске решение до машней задачи № 55. в) Двое учащихся решают по карточкам ин- диивидуального опроса. 1. Плоскости а и р параллельны, прямая т параллельна плоскости р. . Две стороны треугольника параллельны плоскости а. Докажите, что и третья сторона параллельна плоскости а.
. Две стороны треугольника параллельны плоскости а. Докажите, что и третья сторона параллельна плоскости а. . Решение задачи 58
. Решение задачи 58  ано', а || р, ЛАВС,А} = а n АВ, А2 = р п АВ, Bi = а п АС, В2
ано', а || р, ЛАВС,А} = а n АВ, А2 = р п АВ, Bi = а п АС, В2 
 спользовать модели нескольких тетраэдров, а также гибкую модель из картона и ниток (рис. 2).
спользовать модели нескольких тетраэдров, а также гибкую модель из картона и ниток (рис. 2). 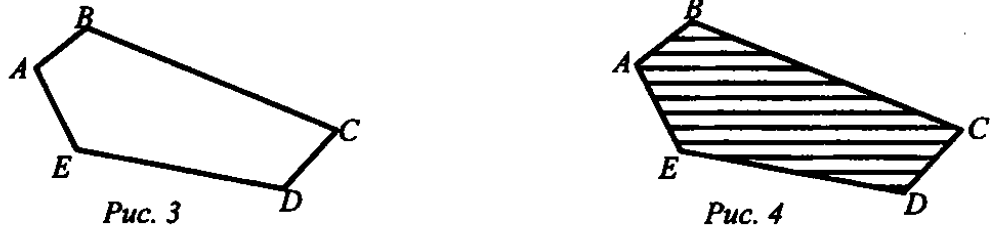
 так, поверхность, составленная из четырех треугольников ДАВС, ДРАВ, &DBC и ДЛСА, на зывается тетраэдром и обозначается: DABC.
так, поверхность, составленная из четырех треугольников ДАВС, ДРАВ, &DBC и ДЛСА, на зывается тетраэдром и обозначается: DABC. . DB cz (ADB), то NK n (ADB) = Mi.
. DB cz (ADB), то NK n (ADB) = Mi. 