10классматематика. Целые и рациональные числа
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
AADC по двум углам. = ----- (поЦели: 1) ввести понятие скрещивающихся прямых; сформулировать и доказать признак скрещивающихся прямых; рассмотреть возможные случаи взаимного расположения прямых в пространстве; 2) развивать логическое и пространственное мышление, развивать владение математической речью; умения делать выводы, обобщать и конкретизировать. 3) воспитывать умение работать в коллективе; воспитывать познавательную активность, самостоятельность, стремление расширять свой кругозор; Ход урока Организационный момент Актуализация опорных знаний учащихся 1. Две прямые в пространстве называются параллельными, если они не пересекаются. 2. Прямая а пересекает плоскость α и а║b.Тогда прямая b не пересекает плоскость α. 3. Прямая и плоскость называются параллельными, если они не имеют общих точек. 4. Прямая а║b, а b ║с. Тогда а ∩с. Изучение нового материала. Б 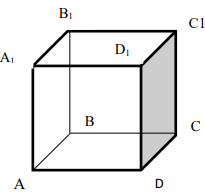 еседа учителя и учащихся по еседа учителя и учащихся попараллелепипеду, по взаимному расположению прямых. -Являются ли параллельными прямые АА1 и DD1; AA1 и CC1? Почему? -Являются ли АА1 и DC параллельными? Они пересекаются? -Прямые АА1 и DC являются скрещивающимися. Сформулируйте определение скрещивающихся прямых. -Какую вы можете поставить цель сегодняшнего урока? Учитель еще раз проговаривает тему, конкретизирует цель и задачи урока. Работа с учебником страница 15. - Работаем самостоятельно с учебником. Списать определение скрещивающихся прямых. Нарисовать рис.20. - Приведите примеры скрещивающихся прямых с помощью модели многогранников (параллелепипед, тетраэдр), на примере классной комнаты. - Приведите примеры скрещивающихся прямых из жизни. - Самостоятельно оформите в тетради доказательство признака скрещивающихся прямых. - Докажите сами теорему о скрещивающихся прямых. Оформите ее в тетрадях. - Давайте еще раз повторим 3 возможных случая взаимного расположения двух прямых в пространстве: 1) прямые пересекаются, т.е. имеют только одну общую точку; 2) прямые параллельны, т.е. лежат в одной плоскости и не пересекаются; 3) прямые скрещиваются, т.е. не лежат в одной плоскости и не пересекаются. Закрепление. Работа с учебником Решить самостоятельно: I вариант – выполнение № 34(а,б), №35 II вариант – выполнение № 34(в,г), №36 Проверка самостоятельной работы упражнения № 34. Подведение итогов - Давайте вспомним с вами, какую цель мы ставили в начале нашего урока. - Достигнута ли нами цель урока? - Какие знания нам пригодились при выполнении заданий на уроке? Домашняя задание № 35,36; выучить доказательство теоремы. Математика 10 класс Урок №20 Дата ___________ Тема: Углы с сонаправленными сторонами Цели: 1) Ввести формулировку и доказательство теоремы о равенстве углов с сонаправленными сторонами; проверить знания по теме «изображение объектов в пространстве». 2) 3) Ход урока Организационный момент Актуализация опорных знаний учащихся 1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны? 2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) Пересекаться? б) Быть скрещивающимися? 3. Могут ли скрещивающиеся прямые и быть параллельными прямой ? 4. Даны две скрещивающиеся прямые и. Точки и лежат на прямой, точки и лежат на прямой. Как будут расположены прямые и? 5. Прямая скрещивается с прямой, а прямая скрещивается с прямой. Следует ли из этого, что прямые и - скрещиваются? 6. Каково должно быть взаимное расположение трех прямых, чтобы можно провести плоскость, содержащую все прямые? И 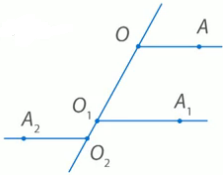 зучение нового материала. зучение нового материала.Любая прямая, например ОО1 (Рис.), рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными. Лучи О2А2 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. Теорема. Если стороны двух углов сонаправленны, то такие углы равны. (доказательство на доске и в тетрадях) Работа по теме урока №34, 35, 38, 41, 42, 43 Подведение итогов урока Домашнее задание № 45, 47, 90 Математика 10 класс Урок №21 Дата ___________ Тема: Угол между прямыми Цели: 1) Ввести понятие угла между прямыми, учить находить углы между скрещивающимися прямыми. Рассмотреть задачи в которых используются эти понятия 2) Средствами урока воспитывать у учащихся ответственное отношение к учебному труду, волевые качества личности, умение работать в коллективе. 3) способствовать развитию пространственного воображения учащихся, умений обосновывать или опровергать выдвигаемые предположения при решении геометрических задач, создать условия для формирования ключевых компетенций учащихся. Ход урока Организационный момент Актуализация опорных знаний учащихся - Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны? - Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться? б) быть скрещивающимися? - Могут ли скрещивающиеся прямые a и b быть параллельными прямой с? - Даны две скрещивающиеся прямые а и b. Точки А и А1 лежат на прямой а, точки В и В1 лежат на прямой b. Как будут расположены прямые АВ и А1В1? - Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с - скрещиваются? Изучение нового материала. Расположение прямых в пространстве и угол между ними. 1. Пересекающиеся прямые. 2. Параллельные прямые. 3. Скрещивающиеся прямые. Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.  Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения. 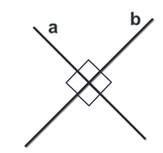 Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°. Угол между двумя параллельными прямыми равен 0°. 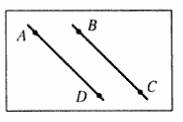 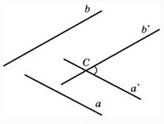 Проговорить метод параллельного переноса при нахождении угла между скрещивающимися прямыми. Закрепление нового материала Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b. 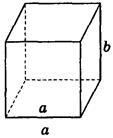 а) 90°; а) 90°; 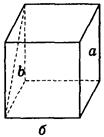 б) 45°; б) 45°;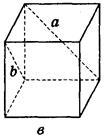 в) 60°; в) 60°; 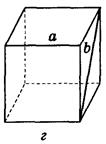 г) 90°; г) 90°;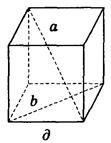 д) 90°; д) 90°; 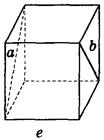 е) 90°. е) 90°.1. Устно. Дан куб ABCDA1B1C1D1 (рис. 4). Найдите угол между прямыми. 1) ВС и СС1 (90°); 2) АС и ВС(45°); 3) D1C1 и ВС(90°). 4) А1В1 и АС(45°). 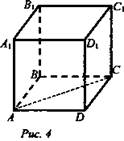 2. Задача № 44 (на доске и в тетрадях). Дано: OB || CD; OA и CD скрещиваются; a) ∠AOB = 40°; б) ∠AOB = 135°; в) ∠AOB = 90° (рис. 5). Найти: угол между ОА и CD. 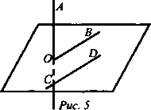 № 40. Дано: а скрещиваются b; Определить: 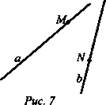 а) а ⊂ α, так как а скрещиваются b, то b ⊄ α. б) 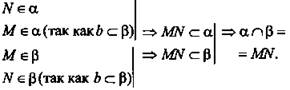 Подведение итогов. Домашнее задание П. 8; 9 № 40; 42. Математика 10 класс Урок №22 Дата ___________ Тема: Контрольная работа по теме: «Взаимное расположение прямых в пространстве» Цели: 1) Повторить основные определения и понятия стереометрии, связанные с взаимным расположение прямых в пространстве; 2) Развивать у учащихся умения анализировать задачу перед выбором способа ее решения; развивать навыки исследовательской деятельности, синтеза, обобщения; 3) Предоставить учащимся возможность осознать значимость себя, почувствовать уверенность в своих силах; Ход урока Организационный момент Контрольная работа Вариант 1 Даны параллельные плоскости α и β. Через точки А и В плоскости проведены параллельные прямые, пересекающие плоскость β в точках А1 и В1. Найдите А1В1, если АВ = 5 см. Верно, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости? Две плоскости параллельны между собой. Из точки М, не лежащей ни в одной из этих плоскостей, ни между плоскостями, проведены две прямые, пересекающие эти плоскости соответственно в точках А1 и A2, В1 и В2. Известно, что МА1 = 4 см, В1В2 = 9 см, A1A2 = МВ1. Найдите МА2 и MB2. Вариант 2 Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями. Найдите АВ, если CD = 3 см. Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости? Из точки О, лежащей вне двух параллельных плоскостей α и β, проведены три луча, пересекающие плоскости α и β соответственно в точках А, В, С и А1, В1, С1 (ОА < ОА1). Найдите периметр А1В1С1, если ОА = m, АА1 = n, АВ = b, ВС = а. Подведение итогов Домашнее задание: решить задачи, с которыми ученик не справился. Математика 10 класс Урок №23 Дата ___________ Тема: Параллельные плоскости Цели: 1) Ввести понятие параллельных плоскостей; 2) Доказать признак параллельности двух плоскостей; 3) Сформировать у учащихся навыки применения этого признака при решении задач. Ход урока Организационный момент Актуализация знаний учащихся Анализ контрольной работы. 1. Подвести итоги контрольной работы. 2. Анализ ошибок, допущенных в работах. Подготовка учащихся к восприятию нового материал. - Сформулировать Аз. - Сформулировать утверждение 1° п. 6. - Признаки подобия треугольников. - Теорема об отношениях площадей подобных треугольников. - Свойство средней линии треугольника. 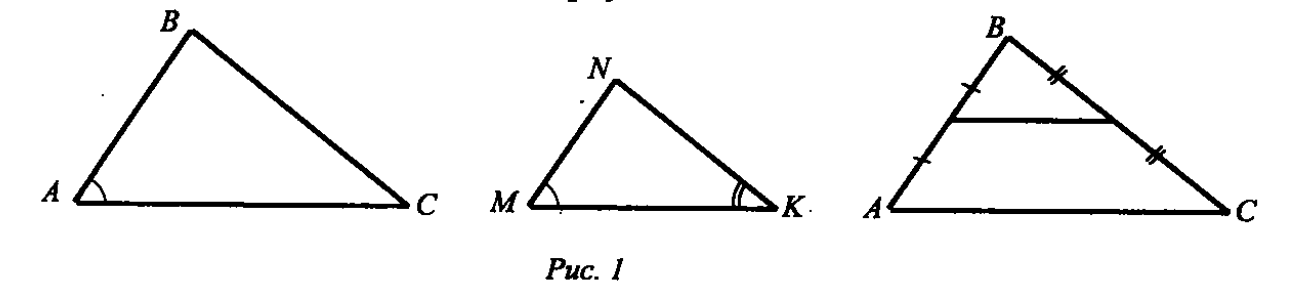 Изучение нового материала 1. Определение параллельных плоскостей. 2. По аксиоме 3 плоскости пересекаются по прямой. Но возможен еще один случай взаимного расположения двух плоскостей, если они не имеют общей точки. На доске схема  В тетрадях учащихся и на доске рисунки и записи.  3 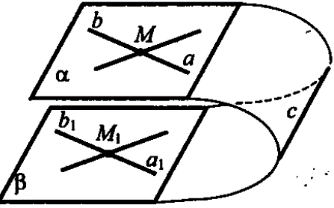 . Признак параллельности плоскостей. . Признак параллельности плоскостей.Дано', a n р = М, а е а, b е а. ai n bl9 а\ g р, bi е р. а || b || (рис. 3). Доказать: а || р. Доказательство: От противного. Пусть а п р = с, 1) Тогда а || р, а а а, а п р = с, значит, а || с (по утверждению 1° п. 6). 2) b || р, b с: а, а п р = с, значит, b || с. 3) Имеем а || Ь, то есть через точку М а ||р проходят две прямые а и Ь, параллельные прямой с. Получили про тиворечие. Значит, а || р. Закрепление изученного материала Ле 51. (еще один признак параллельности плоскостей). Дано: т с\ п = X, т е а, п е а, т || р, п || р (рис. 4). Доказать: а || р. Д 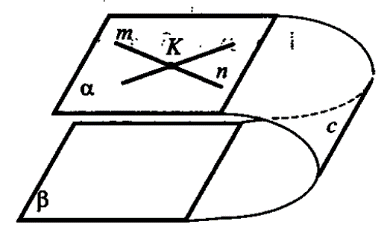 оказательство: Допустим, что а и р не параллельны. Тогда они пересекаются по некоторой прямой с. Так как т || р, п || р, то по утверждению 1° т || с, п || с. Получаем, что через точку К проходят две прямые, параллельные прямой с, что невозможно по. теореме о параллельных прямых. Получили противоречие. Значит, а || р. оказательство: Допустим, что а и р не параллельны. Тогда они пересекаются по некоторой прямой с. Так как т || р, п || р, то по утверждению 1° т || с, п || с. Получаем, что через точку К проходят две прямые, параллельные прямой с, что невозможно по. теореме о параллельных прямых. Получили противоречие. Значит, а || р. №53, Дано\ отрезки А\А2, В Д 2, С[С2 лежат в одной плоскости и имеет об- ю середину - точку О (рис. 5). 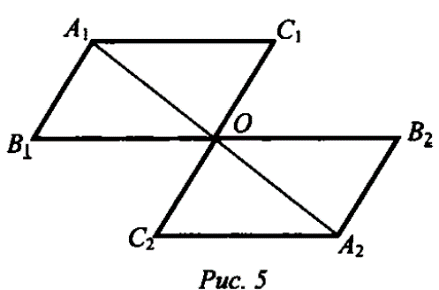 Доказать: АД\С\ ЦА2В2С2. Доказательство: 1) А\А2 и В Д 2 лежат в одной плоско сти по следствию из А\ (через две пересекающиеся прямые проходит плоскость, и притом только одна). А Д \А 2В2 - параллелограмм (диагонали четырехугольника пересекаются и в точке пересечения делятся пополам). Следовательно, А Д } ЦА2В2. 2) Аналогично Л1Л2 и С]С2 лежат в одной плоскости. А\С\А2С2 |

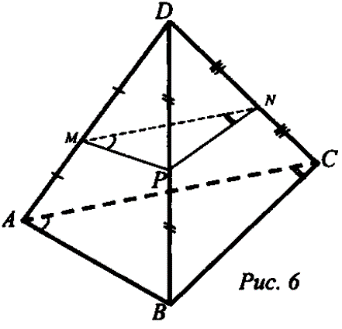 о признаку параллельности плоскостей АД\С\ || А2В2С2.
о признаку параллельности плоскостей АД\С\ || А2В2С2.