10классматематика. Целые и рациональные числа
 Скачать 1.27 Mb.
|
|
Тема: АРИФМЕТИЧЕСКИЙ КОРЕНЬ НАТУРАЛЬНОЙ СТЕПЕНИ Цели: 1) Знать определение арифметического корня натуральной степени, свойства корня п-й степени. 2) Развивать практические умения и навыки учащихся. 3) Воспитывать чувство коллективизма, умение работать в парах Ход урока Организационный момент. Проверка домашнего задания Теоретическая часть. Решим уравнение:  Итак, уравнение имеет два действительных корня ( корни 4-ой степени из числа 81). Положительный корень из числа 81 называют арифметическим корнем четвертой степени из числа 81. Т.о.  .ОПР. Арифметическим корнем натуральной степени n  из неотрицательного числа а называется неотрицательное число, n-ая степень которго равна а.a  :  .Арифметический корень 2-ой степени- квадратный корень, 3-ей степени- кубический. Рассотрим свойства арифметического корня натуральной степени:  4)   5)   6) если n-нечет n=2k+1  n-четное n=2k  Практическая часть. №27 №28, 29 № 32 (1; 3; 5)- № 33-36 (1,3) №33 1)3,5; 3)20; №34 1)35; 3) 1,6; № 35 1) 10; 3) 6; №36 1)72; 3) 3. № 42, № 43 (1, 3 №42(1): V. Домашнее задание: № 32 (2,4,6), № 42 (2,4 VI. Итог урока. Вопросы по теории: Что такое арифметический корень натуральной степени? Какие свойства корня вы знаете? . Математика 10 класс Дата ___________ Тема: АРИФМЕТИЧЕСКИЙ КОРЕНЬ НАТУРАЛЬНОЙ СТЕПЕНИ Цели: 1) уметь применять свойства арифметического корня при решении задач 2) Развивать практические умения и навыки учащихся. 3) Воспитывать положительную мотивацию к изучаемому предмету Ход урока I. Организационный момент Проверка домашнего задания II. Практическая часть №34 № 35 №36 № 42, № 43 (1, 3) №42(1): III. Домашнее задание: ), № 43 (2,4), № 50. Математика 10 класс Дата ___________ Тема: СТЕПЕНЬ С РАЦИОНАЛЬНЫМ И ДЕЙСТВИТЕЛЬНЫМ ПОКАЗАТЕЛЕМ Цели: 1) Знать определение степени с рациональным показателем, свойства этой степени; 2)Развивать практические умения и навыки учащихся. 3) Воспитывать положительную мотивацию к изучаемому предмету   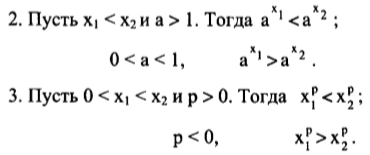 III. Практическая часть. №55, №56 № 55 (1) №56 (1) № 60 (1) IV. Домашнее задание: № 69 (2), № 70 (2, 4), № 85 (2,4). V. Итог урока. Что нового узнали на уроке? (В виде беседы с классом.) Математика 10 класс Дата ___________ Тема: СТЕПЕНЬ С РАЦИОНАЛЬНЫМ И ДЕЙСТВИТЕЛЬНЫМ ПОКАЗАТЕЛЕМ Цели: 1) определение степени с действительным показателем, теорему и три следствия из нее 2) воспитание коммуникативной и информационной культуры обучающихся; 3) эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание на доске и в тетради. Ход урока I. Организационный момент Проверка домашнего задания II. Практическая часть вычислим  Мы можем представить  , тогда Таким образом, мы можем записать  или  На основании данного примера можно сделать вывод: Если n- натуральное число,  , m- целое число и частное  является целым числом, то при  0 справедливо равенство: .Напомним, что r-рациональное число вида , где m- целое число , n- натуральное число. Тогда по нашей формуле получим: Таким образом, степень определена для любого рационального показателя r и любого положительного основания а. Если  , то выражение  имеет смысл не только при 0, но и при а=0, причем,  Поэтому считают, что при r 0 выполняется равенство  Пользуясь формулой степень с рациональным показателем можно представить в виде корня и наоборот.№ 70 (3) №71 (1-3) №72, № 73 №76 III. . Домашнее задание: № 71 (2, 4), № 79 Математика 10 класс Дата ___________ Тема: СТЕПЕНЬ С РАЦИОНАЛЬНЫМ И ДЕЙСТВИТЕЛЬНЫМ ПОКАЗАТЕЛЕМ Цели: 1) уметь выполнять преобразование выражений, используя свойства степени, сравнивать выражения, содержащие степени с рациональным показателем 2) развитие навыка само- и взаимоконтроля; развитие интеллектуальных способностей, мыслительных умений, 3) воспитание познавательного интереса к предмету, воспитание ответственности за выполняемую работу, способствовать созданию атмосферы активного творческого труда. Ход урока I. Организационный момент Проверка домашнего задания II. Практическая часть Учащиеся у доски - разбор упражнений из учебника №70. № 80, №82, №83 III. Домашнее задание №96(2,6), №103(2,4), №110 Математика 10 класс Дата ___________ Тема: Решение задач по теме действительные числа Цели: 1) что такое натуральное, целое, рациональное число, иррациональное число действительные числа, периодическая дробь; вспомнить правила записи бесконечной десятичной дроби в виде обыкновенной, повторить особенности бесконечно убывающей геометрической прогрессии, обобщить правила работы со степенями. 2) Развивать навыки и умения, в выполнении заданий по теме, умение работать в группе и самостоятельно. 3) Воспитывать интерес к математике путём введения разных видов закрепления материала Ход урока: 1. Организационный момент Проверка домашнего задания II. Практическая часть 1) Множества чисел Какова взаимосвязь множества чисел? СМА ВЫБОР Соотнести число с множеством - работа в группах СМА ПРОТИВОРЕЧИЕ Определить допущенную ошибку 2) периодические десятичные дроби Какая дробь называется бесконечной периодической? Работа у доски - №93(1,3) Работа в группах - №93(2,4) 3) Бесконечно убывающая геометрическая прогрессия Какая прогрессия называется бесконечно убывающей? Какова формула суммы такой прогрессии? №22(1) – у доски №22(2) – работа в группах 4)Работа со степенями Какие свойства мы применяем при работе со степенями? – работа в группах (продолжить формулу) №77(2) – у доски №78(2) – у доски №77(1) – в группах №78(1) – в группах №84(1,3,) - у доски №84(2,4) – в группах Контроль усвоения (по ситуации) (5мин) III. Подведение итогов Домашнее задание №94, №95 Математика 10 класс Дата ___________ Тема: Контрольная работа по теме Действительные числа Цели: 1) уметь выполнять преобразование выражений, используя свойства степени, сравнивать выражения, содержащие степени с рациональным показателем 2) развитие навыка само- и взаимоконтроля; развитие интеллектуальных способностей, мыслительных умений, 3) воспитание познавательного интереса к предмету, воспитание ответственности за выполняемую работу, способствовать созданию атмосферы активного творческого труда. Ход урока: 1. Организационный момент Проверка домашнего задания II. Выполнение письменной контрольной работы   III. Подведение итогов Домашнее задание №99, №100 Математика 10 класс Дата ___________ Тема: Предмет стереометрия Цели: 1) ознакомить учащихся с курсом стереометрии, ввести понятие стереометрии, основных фигур стереометрии, рассмотреть аксиомы стереометрии. 2) умение выстраивать аргументацию, приводить примеры и контрпримеры 3) умение организовывать и планировать учебное сотрудничество с учителем и сверстниками, умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем Ход урока: I. Организационный момент II Изучение нового материала Стереометрия – это раздел геометрии, который изучает свойства фигур в пространстве. Основные фигуры стереометрии: точка, прямая, плоскость. Аксиома – это утверждение, которое принимается без доказательства. А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна. А2. Если две точки прямой лежат в плоскости, то и вся эта прямая лежит в плоскости. А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. III. Закрепление с. 7 № 1 а, б, № 2 а, № 3 (устно) № 1 а) PE ϵ (ADB), MK ϵ (BDC), BD ϵ (ADB), (ABC), AB ϵ (ADB), (ABC), CE ϵ (ABC), (DEC) № 1 б) DK ∩ (ABC) в тоске С; CE ∩ (ADB) в точке Е. № 2 а) в плоскости (DCC1); D, D1, C, C1, K, M, R. в плоскости (BQC); B, B1, C, C1, P, M, Q. № 3 а) да, аксиома 1 б) неверно, в) неверно г) неверно IV. Подведение итогов Домашнее задание с. 3-7, решить № 1 в, г, № 2 б Математика 10 класс Дата ___________ Тема: Основные понятия и аксиомы стереометрии Цели: 1) повторить аксиомы планиметрии; изучить аксиомы стереометрии; ознакомить учащихся с содержанием курса стереометрии. 2) сформировать у учащихся представление о стереометрии как о разделе геометрии, изучающем свойства фигур в пространстве, сформулировать основные аксиомы стереометрии; 3) Сформировать представления учащихся об аксиомах стереометрии, взаимном расположении прямой и плоскости, плоскостей в пространстве, способах задания плоскости в пространстве. Ход урока: I. Организационный момент II. Изучение нового материала Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять. Простейшие фигуры в пространстве: точка, прямая, плоскость. Плоскость.  Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны. На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко 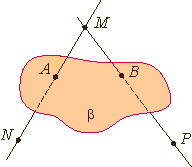 это записывают так: А ∈ β, B ∈ β, Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.  Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую). 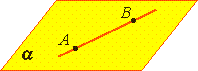 Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются. 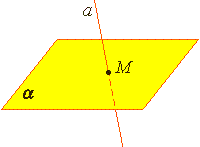 Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты  . Теорема 1. Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.  Теорема 2. Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.  III. Закрепление изученного материала 1. Прочитать формулировки аксиом А1—А3. 2. Решаем задачи: Учащиеся читают условие задачи по учебнику стр. 7—8 и дают ответ с объяснениями. Задача 1 (а, б) с. 7. Ответ: а) Точки Р и Е лежат в плоскости (АDВ), а значит и прямая РЕ лежит в плоскости (АDВ) (по А2). Аналогично МК лежит в плоскости (ВDС). Точки В и D лежат одновременно в плоскостях (АDВ) и (ВDС), а значит прямая ВD лежит в плоскостях (АDВ) и (АВС). Аналогично АВ лежит в плоскостях (АDВ) и (АВС). Точки С и Е лежат одновременно в плоскостях (АВС) и (DЕС), а значит прямая СЕ лежит в этих же плоскостях. б) Заметим, что точка С лежит на прямой (DК) и в плоскости АВС, а следовательно, DК∩(АВС) в точке С, так как точек пересечения более одной (прямая не лежит в плоскости), то это единственная точка. Аналогично СЕ пересекается с плоскостью (АDВ) в точке Е. Задача 2(а) с. 7. Ответ: а) В плоскости DСС1: D, С, С1, D1, К, M, R (см. №1). В плоскости ВQС: В1, В, Р, Q, С1, М, С. Повторить аксиомы планиметрии. Выучить аксиомы А1—А3. Прочитать пункт 1—2. Задача 1(в, г) Ответы: в) в плоскости АDВ лежат точки: А, D, В, Е, Р, М, так как точка Е лежит на прямой АВ, а значит, и в плоскости АВD. В плоскости DВС лежат точки: D, В, С, M, К г) плоскости АВС и DСВ пересекаются прямой ВС, так как обе точки В и С лежат в обеих плоскостях. Аналогично: АВD пересекается с СDА по прямой АD. Так как точка Е принадлежит РD, значит, Е принадлежит РDС и так как точка С принадлежит РDС, то прямая СЕ принадлежит РDС, а так как СЕ принадлежит АВС, то плоскости АВС и РDС пересекаются по прямой СЕ. Задача 2 (б, д) Ответы: б) АА1В1; АА1D1. д) МК∩DС = R; В1С1∩ВР =Q; С1М∩DС = С. IV. Подведение итогов Мы познакомились с новым разделом геометрии — стереометрией, узнали новые аксиомы и использовали их при решении задач. Что нового вы узнали на сегодняшнем уроке? Домашнее задание Повторить аксиомы планиметрии. Выучить аксиомы А1—А3. Прочитать пункт 1—2. Математика 10 класс Дата ___________ |