10классматематика. Целые и рациональные числа
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
|
Математика 10 класс Дата ___________ Тема: ЦЕЛЫЕ И РАЦИОНАЛЬНЫЕ ЧИСЛА Цели: 1) уметь записывать бесконечную десятичную дробь в виде обыкновенной, уметь выполнять действия с десятичными и обыкновенными дробями. 2) Развивать мышление, умение анализировать и делать выводы. 3) Воспитывать чувство коллективизма, умение работать в парах. Ход урока Организационный момент. Проверка домашнего задания Теоретическая часть. Первоначально под числом понимали лишь натуральные числа, которых достаточно для счета отдельных предметов. Множество N = {1; 2; 3; ...} натуральных чисел замкнуто относительно операций сложения и умножения. Это значит, что сумма и произведение натуральных чисел являются числами натуральными. Однако разность двух натуральных чисел уже не всегда является натуральным числом. Приведите примеры. (5- 5 = 0; 5-7 = -2, числа 0 и -2 не являются натуральными.) Так, результат вычитания двух одинаковых натуральных чисел приводит к понятию нуля и введению множества целых неотрицательных чисел Хо = {0; 1; 2;...}, Чтобы сделать выполнимой операцию вычитания, вводят отрицательные целые числа, то есть числа, противоположные натуральным. Таким образом получают множество целых чисел. X = {...-3; -2; -1; 0; 1; 2; ...}. Чтобы сделать выполнимой операцию деления на любое число, не равное нулю, необходимо к множеству всех целых чисел присоединить множество всех положительных и отрицательных дробей. В результате получается множество рациональных чисел. 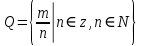 При выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа. Каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби. Вспомним, что такое периодическая дробь. Это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр - период дроби. Например, 0,3333... = 0,(3) 1,057373... = 1,05(73). Читаются эти дроби так: «0 целых и 3 в периоде», «1 целая, 5 сотых и 73 в периоде». Запишем рациональные числа в виде бесконечной периодической десятичной дроби: натуральное число 25 = 25,00... = 25,(0); целое число -7 = -7,00... = -7,(0); обыкновенная дробь = -2,300... = -2,3(0); & = 1,533... = 1,5(3). Воспользуемся алгоритмом деления уголком: Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом, так как может быть представлена в виде дроби —, где ш - целое п  Нужно умножить дробь на 10п, где п - количество десятичных знаков, содержащихся в записи этой дроби до периода: х-10п. Умножаем на 10к, где к - количество цифр в периоде. х-10п 10к = х-10п+к. Отнимем от равенства (2) равенство (1), решим полученное уравнение. число, п - натуральное число. Рассмотрим в качестве примера задачу 2 из параграфа учебника и составим алгоритм.Пусть х = 0,2(18). Умножая на 10, получаем 10х = 2,1818... Умножая обе части последнего равенства на 100, находим 1000х = 218,1818... Вычитая из равенства (2) равенство (1), получаем 990х = 216. Ш. Практическая часть. № 1(1)-на доске. №1(3)-под диктовку. (Все учащиеся выполняют задание в тетрадях, один ученик проговаривает вслух решение.) № 1(5)-самостоятельно. (Учащиеся выполняют задание в тетрадях. Выполнив задание, ученик поднимает руку. Дождавшись, когда весь класс или его большая часть справится с заданием, проверяем решение. Либо учитель опрашивает нескольких учеников, либо один ученик сообщает ответ и выясняем, нет ли другого ответа, либо учитель сам сообщает верный ответ. Желательно использовать сигнальные карточки - карточки с одной стороны зеленого цвета, с другой - красного. Каждый ученик имеет такую карточку, если он согласен с прозвучавшим ответом, то показывает учителю зеленую сторону карточки, если не согласен - красную.) № 2(1) № 2(3) № 2(5) № 3(6) №4 № 5(1) Домашнее задание: № 1 (2, 4, 6), № 2 (2, 4, 6), № 3 (2, 4), № 5 (2). Итог урока: по вопросам. Множества каких чисел вы знаете? {Натуральные, целые, рациональные). Приведите примеры. Что такое периодическая дробь? Как записать ее в виде обыкновенной? Математика 10 класс Дата ___________ Тема: ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА Цели: 1) уметь выполнять вычисления с иррациональными выражениями, сравнивать числовые значения иррациональных выражений. 2) Развивать практические умения и навыки учащихся. 3) Воспитывать положительную мотивацию к изучаемому предмету Ход урока Организационный момент. Проверка домашнего задания Теоретическая часть. Необходимость дальнейшего расширения множества чисел связана в основном с двумя причинами. Во-первых, рациональных чисел недостаточно для выражения результатов измерений (например, нельзя выразить рациональным числом длину диагонали квадрата со стороной 1). Во-вторых, такие числовые выражения, как 73 , 1/5,8Ш 1°ит. д., не являются рациональными числами. Объединение множества рациональных чисел и множества иррациональных чисел (бесконечных десятичных непериодических дробей) дает множество К действительных чисел. Действительным числом называется бесконечная десятичная дробь, то есть дробь вида +ао,а]а2а3 ... или-ао^агаз..., где ао - целое неотрицательное число, а каждая из букв а1,а2,а3 ... - это одна из десяти цифр: 0, 1,2, 3, 4, 5, 6, 7, 8, 9. Арифметические операции над действительными числами обычно заменяются операциями над их приближениями. Например, 72 = 1,4142135... 7з= 1,7320508.... Вычислим сумму с точностью до единицы: 72+73= 1,4+ 1, 7 = 3,1 = 3; с точностью до десятой: 72+7з = 1,41 + 1,73 = 3,14 = 3,1; с точностью до сотой: 72 + 73 = 1,414+ 1,732 = 3,146 = 3,15 и т.д. Числа 3; 3,1; 3,15 и т. д. являются последовательными приближениями значения суммы 72 + 7з. Пусть X], Хг, ..., хп, ... - последовательные приближения действительного числа х с точностью до 1, до 0,1, до 0,01 и т. д. Тогда погрешность приближения | х - хп | как угодно близко приближается к нулю. | х - хп | —> 0 при п —> 00 или Нт | х - хп I =0 (Читается: «| х - хп I стремится к нулю при и, стремящемся к бесконечности» или «предел | х - хп I при п, стремящемся к бесконечности, равен нулю».) То есть, хп —> х при п —> со или Нт хп = х Все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т. д.). Модуль действительного числа х обозначается | х | и определяется так же, как и модуль рационального числа: 'х, если х > 0, .-х, если х < 0. Практическая часть. №6. № 8 №9(1,3,5) №10(1) № 10 (2) №10(3) №10 (4) № 11(1) №12 IV Домашнее задание: № 9 (2, 4, 6), № 11 (2), № 93. V Итог урока. Провести самоанализ (Чему я научился на этом уроке: Что нового узнал?) Математика 10 класс Дата ___________ Тема: БЕСКОНЕЧНО УБЫВАЮЩАЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ Цели: 1) Знать, какая прогрессия называется геометрической, что такое бесконечно убывающая геометрическая прогрессия, 2) Развивать практические умения и навыки учащихся. 3) Воспитывать чувство коллективизма, умение работать в парах Ход урока I. Организационный момент Проверка домашнего задания II. Теоретическая часть. 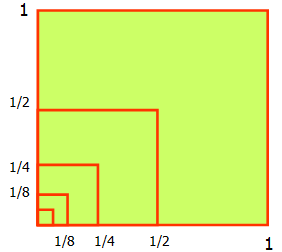 Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего. В результате, мы получили последовательность сторон квадратов И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например, 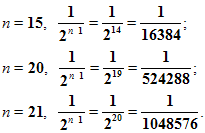 Т.е. с возрастанием номера n члены прогрессии приближаются к нулю. С помощью этого рисунка можно рассмотреть и ещё одну последовательность.  Например, последовательность площадей квадратов: 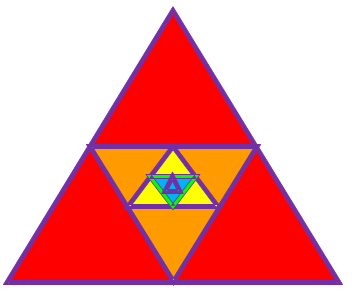 И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю. И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников. Если рассмотреть геометрическую прогрессию с отрицательным знаменателем. То, опять, с возрастанием номера n члены прогрессии приближаются к нулю. Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю. Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1. Определение: Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы. С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет. Задача Является ли последовательность бесконечно убывающей геометрической прогрессией, если она заданна формулой: Решение: данная геометрическая прогрессия является бесконечно убывающей. б) данная последовательность не является бесконечно убывающей геометрической прогрессией. Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию: Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1. Но в левой части этого равенства – сумма бесконечного числа слагаемых. Рассмотрим сумму n первых слагаемых. По формуле суммы n первых членов геометрической прогрессии, она равна 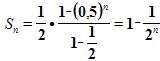 . .Если n неограниченно возрастает, то или Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S1, S2, S3, …, Sn, … . Например, для прогрессии имеем 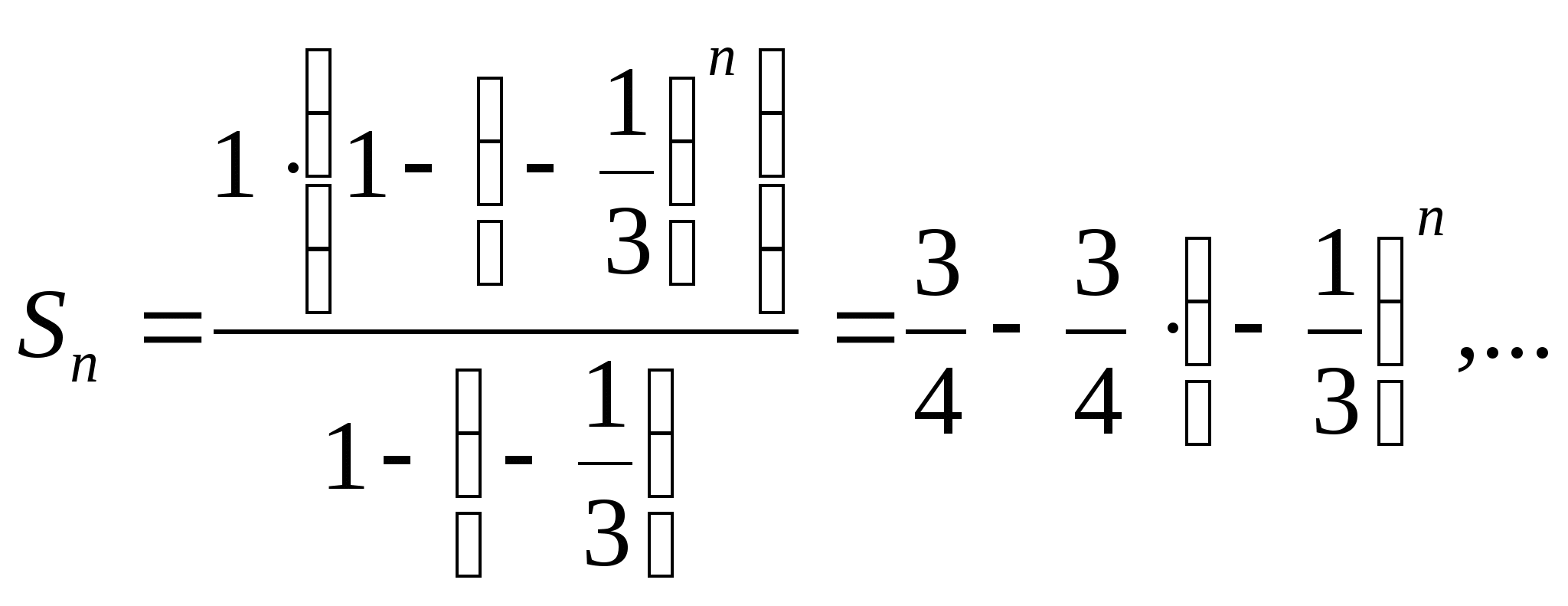 Так как Так как Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле III. Практическая часть. № 16 № 16 (3)-устно. №16(4) № 17 (1, 3, 4) № 20 (3) №21 (1) №21 (3) №22(1) IV. Подведение итогов. С какой последовательностью сегодня познакомились? Дайте определение бесконечно убывающей геометрической прогрессии. Как доказать, что геометрическая прогрессия является бесконечно убывающей? Назовите формулу суммы бесконечно убывающей геометрической прогрессии. Домашнее задание: № 16 (2), № 17 (2), № 21 (2,), № 22 (2), № 23 (2). Математика 10 класс Дата ___________ Тема: БЕСКОНЕЧНО УБЫВАЮЩАЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ Цели: 1) знать формулу суммы бесконечно убывающей геометрической прогрессии, уметь применять эту формулу при решении задач, в частности при записи бесконечной периодической десятичной дроби в виде обыкновенной. 2) Развивать мышление, умение анализировать и делать выводы 3) Воспитывать чувство коллективизма, умение работать в парах Ход урока I. Организационный момент. Проверка домашнего задания II. Практическая часть. Работа организована индивидуально у доски и в тетрадях с дифференцированной степенью самостоятельности. Критерием достижения положительного результата этапа является знание всеми учащимися алгоритма нахождения суммы БУГП. Коррекция осуществляется с помощью взаимопроверки. Используются упражнения 18(1,2) Найти сумму БУГП: 1. 2. а также упражнения из дидактических материалов по алгебре и началам анализа Б.Г.Зива и В.А. Гольдича, с/р №2, упражнения 1 из вариантов 1 и 2. Найти сумму БУГП: 1. 2. Желающим, справившимся с общим заданием раньше других, предлагается обратная задача: Известна сумма БУГП и второй член прогрессии. Нужно найти первый член прогрессии и знаменатель: дано: найти q и За самостоятельное решение этой задачи выставляется отдельная оценка. 5 этап. Первичное обобщение и включение нового знания в систему субъектного опыта учащихся. Установление содержательных взаимосвязей БУГП с линиями уравнений и действительных чисел. Фронтально решается задача распознавания БГУП. С помощью этой задачи, с одной стороны, осуществляется диагностика достижения положительного результата предыдущих этапов урока, с другой стороны, полученные результаты позволяют осуществить содержательные взаимосвязи по выше указанным линиям. Из предложенных последовательностей выбрать БУГП: 1) 2) 3) 4;2;1; и т.д.; 4) 5) 6) 7) 8) Таковыми являются 2); 3); 5); 6); 7) и 8). Сначала найдём сумму БУГП из задания 8). Для этого запишем сумму членов прогрессии и воспользуемся формулой суммы БУГП. Получим: 1+ Установление содержательных взаимосвязей БУГП с линией уравнений Сравните полученный результат с уравнением и воспользуйтесь при его решении полученным результатом: Уравнение 1) Заметим, что если к обеим частям равенства прибавить 1, то можно воспользоваться полученным выше результатом: Итак, мы получили дробное рациональное уравнение, алгоритм решения которого известен школьникам. Уравнение 2) 2 ¦x¦<1. Решение уравнения 1) проводится учеником на доске, уравнение 2 предлагается для самостоятельной работы дома. Делается весьма неожиданный вывод о том, что сумма БГУП даёт возможность решения некоторых уравнений, имеющих бесконечное число членов. Таким образом, удаётся установить содержательную связь БУГП с линией уравнений. Установление содержательных взаимосвязей БУГП с линией действительных чисел. К доске приглашаются 3 ученика для решения задач 1-3. 1) Сначала находим сумму БУГП по формуле S= Затем попытаемся осмыслить, что представляет собой сумма членов этой прогрессии, если её члены записать в виде десятичных дробей: 0,3+0,03+0,003+….=0,3333…=0,(3). Таким образом, видим, что с помощью формулы суммы БУГП можно осуществлять переход от записи действительного числа в виде бесконечной периодической дроби к записи в виде обыкновенной дроби. 2) Эта задача носит дублирующий характер и используется для создания условий лучшего осмысления сформулированного вывода. 3) III. Подведение итогов. Домашнее задание: № 21 ( 4), № 22 (2), № 23 (2). Математика 10 класс Дата ___________ |
