Цифровые устройства. Что такое цифровые микросхемы. Виды цифровых микросхем

• Название: Что такое цифровые микросхемы. Виды цифровых микросхем
• Анкор: Цифровые устройства.doc
• Дата: 22.09.2017
• Размер: 2.25 Mb.
• Имя файла: Цифровые устройства.doc
• Тип: Документы; #8922
• страница: 22 из 38

Глава 10

Универсальные регистры

Регистры сдвига выполняют обычно как универсальные последовательно-параллельные микросхемы. Это связано с необходимостью записи в регистр параллельного двоичного кода при преобразовании параллельного кода в последовательный.

Переключение регистра из параллельного режима работы в последовательный и наоборот осуществляется при помощи мультиплексора (коммутатора). Использование коммутатора позволяет входы D триггеровуниверсального регистра либо подключать к внешним выводам микросхемы, либо подключать к выходу предыдущего триггера.

Напомню, что двухвходовый мультиплексор можно реализовать при помощи логических элементов “2И-2ИЛИ”. Элементы “И” при этом работают в качестве электронных ключей, а элементы “ИЛИ” объединяют их выходы.

Схема универсального регистра с использованием коммутаторов на логических элементах “2И-2ИЛИ” приведена на рисунке 10.1.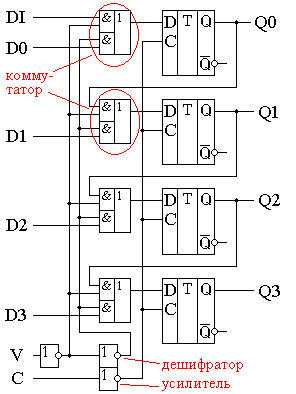

 
Рисунок 10.1. Принципиальная схема универсального регистра

В этой схеме для переключения регистра из последовательного режима работы в параллельный используется вывод V. Подача на этот вход единичного потенциала превращает схему в параллельный регистр. При этом на входы ключей, подключенных к информационным входам D, подаётся единичный потенциал. Это приводит к тому, что сигналы с входов параллельной записи данных поступают на входы логических элементов “ИЛИ”, а на входы ключей, подключенных к выходам предыдущих триггеров, подаются нулевые потенциалы. То есть на выходах этих ключей будут присутствовать нулевые потенциалы, и они не будут мешать работе.

Подача на вход V нулевого потенциала приводит к отключению входов параллельных данных от входов триггеров. Сигналы же с выхода предыдущего триггера свободно проходит через верхние логические элементы “И” на вход последующего триггера, так как на его второй вход подаётся единичный потенциал.

Инверторы на входах V и C использованы для усиления входного сигнала по току. В результате входной ток микросхемы будет равен не суммарному току четырёх логических элементов “И”, а входному току инвертора.

Условно-графическое изображение универсального регистра приведено на рисунке 10.2. Вход последовательного ввода данных на этом рисунке обозначен как DI и отделён от других групп входов чертой. Точно так же выделены в отдельные группы и входы управления V и синхронизации C.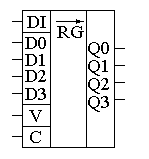


Рисунок 10.2. Обозначение универсального регистра на принципиальных схемах

Глава 11

Счётчики

Счётчики используются для построения таймеров или для выборки инструкций из ПЗУ в микропроцессорах. Они могут использоваться как делители частоты в управляемых генераторах частоты (синтезаторах). При использовании в цепи ФАП счётчики могут быть использованы для умножения частоты как в синтезаторах, так и в микропроцессорах.

Двоичные асинхронные счётчики

Простейший вид счётчика — двоичный может быть построен на основе T-триггера. T-триггер изменяет своё состояние на прямо противоположное при поступлении на его вход синхронизации импульсов. Для реализации T-триггера воспользуемся универсальным D-триггером с обратной связью, как это показано на рисунке 11.1.

 
Рисунок 11.1. Реализация счетного T-триггера на универсальном D-триггере

Так как эта схема, как мы уже рассматривали ранее, при поступлении на вход импульсов меняет свое состояние на противоположное, то её можно рассматривать как счётчик, считающий до двух. Временные диаграммы сигналов на входе и выходах T-триггера приведены на рисунке 11.2.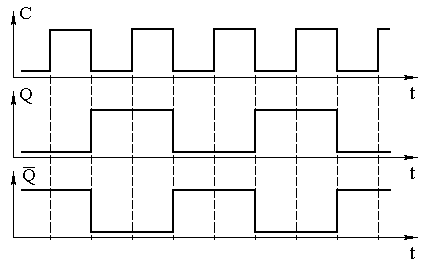



Рисунок 11.2 Временные диаграммы сигналов на входе и выходах T-триггера.

Обычно требуется посчитать большее количество импульсов. В этом случае можно использовать выходной сигнал первого счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два.

Схема счётчика, позволяющего посчитать любое количество импульсов, меньшее шестнадцати, приведена на рисунке 11.3. Количество поступивших на вход импульсов можно узнать, подключившись к выходам счётчикаQ0 … Q3. Это число будет представлено в двоичном коде.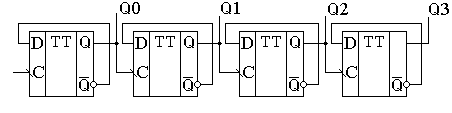

 
Рисунок 11.3. Схема четырёхразрядного счётчика, построенного на универсальных D-триггерах

Для того чтобы разобраться, как работает схема двоичного счётчика, воспользуемся временными диаграммами сигналов на входе и выходах этой схемы, приведёнными на рисунке 11.4.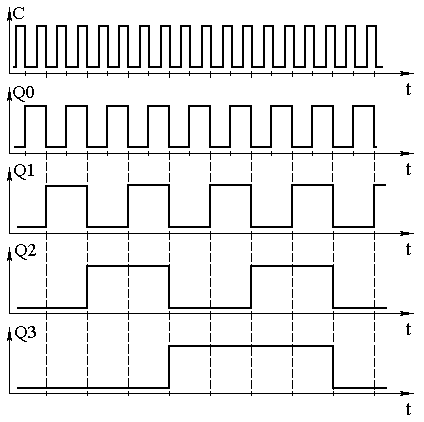

 
Рисунок 11.4 Временная диаграмма четырёхразрядного счётчика

Пусть первоначальное состояние всех триггеров счётчика будет нулевым. Это состояние мы видим на временных диаграммах. Запишем его в таблицу 11.1. После поступления на вход счётчика тактового импульса (который воспринимается по заднему фронту) первый триггер изменяет своё состояние на противоположное, то есть единицу.

Запишем новое состояние выходов счётчика в ту же самую таблицу. Так как по приходу первого импульса изменилось состояние первого триггера, то этот триггер содержит младший разряд двоичного числа (единицы). В таблице поместим его значение на самом правом месте, как это принято при записи любых многоразрядных чисел. Здесь мы впервые сталкиваемся с противоречием правил записи чисел и правил распространения сигналов на принципиальных схемах.

Подадим на вход счётчика ещё один тактовый импульс. Значение первого триггера снова изменится на прямо противоположное. На этот раз на выходе первого триггера, а значит и на входе второго триггера сформируется задний фронт. Это означает, что второй триггер тоже изменит своё состояние на противоположное. Это отчётливо видно на временных диаграммах, приведённых на рисунке 11.4. Запишем новое состояние выходов счётчика в таблицу 11.1. В этой строке таблицы образовалось двоичное число 11.2. Оно совпадает с номером входного импульса.

Продолжая анализировать временную диаграмму, можно определить, что на выходах приведённой схемы счётчика последовательно появляются цифры от 0 до 15. Эти цифры записаны в двоичном виде. При поступлении на счётный вход счётчика очередного импульса, содержимое его триггеров увеличивается на 1. Поэтому такие счётчики получили название суммирующих двоичных счётчиков.

Таблица 11.1. Изменение уровней на выходе суммирующего счётчика при поступлении на его вход импульсов.

номер входного импульса	Q3	Q2	Q1	Q0
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1
10	1	0	1	0
11	1	0	1	1
12	1	1	0	0
13	1	1	0	1
14	1	1	1	0
15	1	1	1	1

Условно-графическое обозначение суммирующего двоичного счетчика на принципиальных схемах приведено на рисунке 11.5. В двоичных счётчиках обычно предусматривают вход обнуления микросхемы R, который позволяет записать во все триггеры счётчика нулевое значение. Это состояние иногда называют исходным состоянием счётчика.

Рисунок 11.5. Четырёхразрядный двоичный счётчик.

Существуют готовые микросхемы асинхронных двоичных счётчиков. Классическим примером такого счётчика является микросхема 555ИЕ5. Подобные схемы существуют и внутри САПР программируемых логических интегральных схем.

Двоичные вычитающие асинхронные счётчики

Счётчики могут не только увеличивать своё значение на единицу при поступлении на счётный вход импульсов, но и уменьшать его. Такие счётчики получили название вычитающих счётчиков. Для реализации вычитающего счётчика достаточно чтобы T-триггер изменял своё состояние по переднему фронту входного сигнала.

Изменить рабочий фронт входного сигнала можно инвертированием этого сигнала. В схеме, приведенной на рисунке 11.6, для реализации вычитающего счётчика сигнал на входы последующих триггеров подаются с инверсных выходов предыдущих триггеров.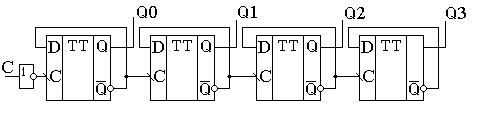



Рисунок 11.6 Схема четырёхразрядного двоичного вычитающего счётчика, построенного на универсальных D-триггерах.

Временная диаграмма этого счётчика приведена на рисунке 11.7. По этой диаграмме видно, что при поступлении на вход счётчика первого же импульса на выходах появляется максимально возможное для четырёхразрядного счётчика число 15₁₀. При поступлении следующих импульсов содержимое счётчика уменьшается на единицу.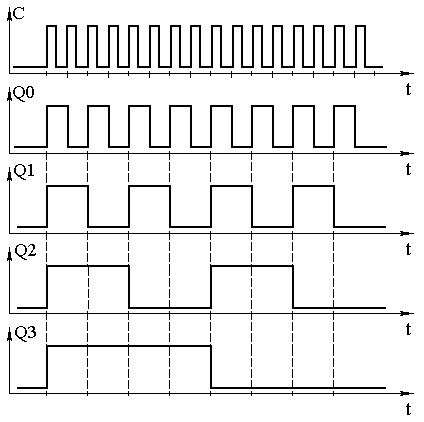



Рисунок 11.7. Временная диаграмма четырёхразрядного вычитающего счётчика.

Это вызвано тем, что при поступлении переднего фронта тактового импульса первый триггер переходит в единичное состояние. В результате на его выходе тоже формируется передний фронт. Он поступает на вход второго триггера, что приводит к записи единицы и в этот триггер. Точно такая же ситуация складывается со всеми триггерами счётчика, то есть все триггеры перейдут в единичное состояние. Для четырёхразрядного счётчика это и будет число 15₁₀. Запишем новое состояние вычитающего счётчика в таблицу 11.2.

Следующий тактовый импульс приведёт к изменению состояния только первого триггера, так как при этом на его выходе сформируется задний фронт сигнала. Запишем и это состояние в таблицу 11.2. Обратите внимание, что при поступлении каждого последующего импульса содержимое счётчика, построенного по анализируемой схеме, уменьшается на единицу. Этот процесс продолжается до тех пор, пока состояние счётчика не станет вновь равно 0. При поступлении новых тактовых импульсов процесс повторяется снова.

Все возможные состояния логических сигналов на выходах вычитающего счётчика, при поступлении на счётный вход схемы тактовых импульсов приведены в таблице 11.2. Таблица 11.2 фактически повторяет временные диаграммы, приведённые на рисунке 11.7, однако она более наглядно представляет физику работы счётчика. Просто мы при работе с числами привыкли иметь дело с цифрами, а не с напряжениями, тем более в зависимости от времени.

Таблица 11.2. Изменение уровней на выходе вычитающего счётчика при поступлении на его вход импульсов.

номер входного импульса	Q3	Q2	Q1	Q0
0	0	0	0	0
1	1	1	1	1
2	1	1	1	0
3	1	1	0	1
4	1	1	0	0
5	1	0	1	1
6	1	0	1	0
7	1	0	0	1
8	1	0	0	0
9	0	1	1	1
10	0	1	1	0
11	0	1	0	1
12	0	1	0	0
13	0	0	1	1
14	0	0	1	0
15	0	0	0	1

Для тех, кто привык работать с реально выпускаемыми микросхемами средней интеграции, следует обратить внимание, что для примера были использованы D-триггеры, работающие по заднему фронту. Микросхемы, выпускаемые промышленностью, например, 1533ТМ2 (два D-триггера в одном корпусе) или SN74LVC1G79 (микросхемы малой логики) срабатывают по переднему фронту, поэтому схемы для суммирующего и вычитающего счётчика поменяются местами.

Следует отметить, что при применении для реализации двоичных счетчиков современных схем большой интеграции, таких как программируемые пользователем вентильные матрицы FPGA, мы можем применять D-триггеры срабатывающие как по переднему (нарастающему), так и по заднему (спадающему фронту).

Глава 12

Недвоичные счётчики с обратной связью

Если посмотреть на временную диаграмму сигналов на выходах двоичного счётчика, приведённую на рисунке 12.1, то можно увидеть, что частота сигналов на его выходах будет уменьшаться в два раза по отношению к предыдущему выходу. Это позволяет использовать счетчики в качестве делителей частоты входного сигнала. Эти делители частоты могут быть использованы в устройствах формирования высокостабильных генераторов частоты (синтезаторов частот).



Рисунок 12.1. Временная диаграмма четырёхразрядного счётчика.

Сформированные частоты могут быть использованы либо для синхронизации различных цифровых устройств (в том числе и микропроцессоров) либо в качестве высокостабильных генераторов опорных частот в радиоприёмных и радиопередающих устройствах.

При использовании цифровых счётчиков в качестве устройств формирования опорных частот часто требуется обеспечить коэффициент деления частоты, отличающийся от степени числа 2. В этом случае требуется счётчик с недвоичным коэффициентом счёта.

Ещё одна ситуация, когда необходимо применять недвоичные счётчики возникает при отображении информации, записанной в счётчике. Человек, который работает с электронной техникой, привык работать с десятичной системой счисления, поэтому возникает необходимость отображать хранящееся в счётчике число в непосредственно десятичном виде. Это намного проще сделать, если и счет вести сразу в двоично-десятичном коде. Иначе для индикации потребуется перекодировать информацию из двоичного кода вдвоично-десятичный код.

Построить недвоичный счётчик можно из двоичного за счёт выбрасывания лишних комбинаций единиц и нулей. Это может быть осуществлено при помощи обратной связи. Для этого при помощи дешифратораопределяется число, соответствующее коэффициенту счёта, и сигнал с выхода этого дешифратора обнуляет содержимое двоичного счётчика. В качестве примера на рисунке 12.2 приведена схема двоично-десятичного счётчика.

 
Рисунок 12.2 Схема десятичного счётчика, построенного на основе двоичного счётчика

В этой схеме дешифратор построен на двухвходовой схеме "2И", входящей в состав микросхемы двоичного счётчика. Дешифратор декодирует число 10 (1010 в двоичной системе счисления). В соответствии с принципами построения схем по произвольной таблице истинности для построения дешифратора требуется ещё два инвертора, подключённых к выходам 1 и 4. Однако после сброса счётчика числа, большие 10 никогда не смогут появиться на выходах микросхемы. Поэтому схема дешифратора упрощается и вместо четырёхвходовой схемы "4И" можно обойтись двухвходовой схемой. Инверторы тоже оказываются лишними.

При использовании счётчиков в качестве делителей частоты тоже можно воспользоваться обратной связью. Приведём в качестве примера схему делителя частоты на 1000. При разработке делителя прежде всего определим сколько потребуется микросхем двоичных счётчиков. Для этого определим степень числа 2, при которой число M=2ⁿ будет больше требуемого числа 1000. Это будет число 10. При возведении основания системы счисления 2 в 10 степень получится число 1024. То есть, при использовании для построения делителя частоты непосредственно триггеров, достаточно будет десяти триггеров. Однако обычно для построения делителей частоты используют готовые двоичные счётчики, поэтому определим необходимое количество микросхем двоичных счётчиков. При использовании четырёхразрядных двоичных счётчиков достаточно будет трёх микросхем, так как в трёх микросхемах будет 3*4=12 триггеров, что заведомо больше минимального числа триггеров.

Следующим этапом построения делителя частоты будет перевод коэффициента деления 1000 в двоичное представление. Десятичное число 1000 в двоичном виде будет выглядеть как 0011 1110 1000. В этом числе шесть единиц, поэтому для построения делителя будет достаточно шестивходовой схемы "И". Однако такие  схемы не выпускаются, поэтому воспользуемся микросхемой "8И-НЕ". Неиспользуемые входы этой микросхемы подключим к питанию. Ненужную нам инверсию сигнала скомпенсируем дополнительным инвертором. Получившаяся принципиальная схема делителя на 1000 приведена на рисунке 12.3.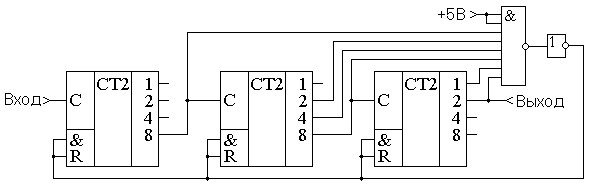

 
Рисунок 12.3 Принципиальная схема делителя на 1000, построенного на основе трёх двоичных счётчиков

При использовании счётчиков в составе синтезаторов частот может потребоваться формирование целого диапазона частот. В этом случае делитель, построенный на недвоичном счётчике, должен обладать возможностью изменения коэффициента деления.

Такие делители частоты получили название делителей с переменным коэффициентом деления (ДПКД). При использовании обратной связи для реализации ДПКД потребуется полный дешифратор и переключатели его выходов на вход сброса счётчика. Схема делителя частоты при этом получается сложной, а управление таким делителем неудобным.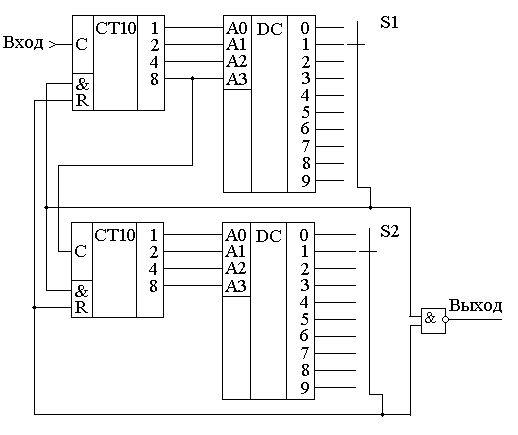

 
Рисунок 12.4. Схема делителя с переменным коэффициентом деления с максимальным коэффициентом деления 100, построенного на основе двух десятичных счётчиков

Пример двухразрядного делителя с переменным коэффициентом деления (ДПКД), построенного на десятичных счётчиках приведён на рисунке 4. Обратите внимание, что для удобного управления таким синтезатором частоты использованы десятичные счётчики. Использование десятичных счетчиков позволяет выставлять необходимую частоту непосредственно в десятичном виде. Значение частоты можно нанести на корпусе прибора под клювиками переключателей или отображать набираемую частоту на десятичных индикаторах.

В качестве ещё одного недостатка такого делителя частоты можно отметить очень маленькую длительность выходных импульсов. Если требуется сформировать строго симметричное колебание, то на выходе такого делителя можно поставить одноразрядный двоичный делитель частоты на T триггере. На выходе двоичного делителя всегда формируется меандр с очень высокой точностью.

Глава 13

Недвоичные счётчики с предварительной записью

В счётчиках с обратной связью исключаются последние состояния двоичного счётчика. Можно поступить по-другому. Начать с последнего состояния счётчика и, воспользовавшись вычитающим счётчиком, определять нулевое состояние счётчика. Это состояние очень просто можно определить при помощи логического элемента "И". В данной схеме начинать счёт необходимо с числа, которое будет определять коэффициент деления делителя, построенного на таком счётчике.

При построении счётчика по таким принципам необходимо иметь возможность предварительной записи в счётчик. То есть счётчик при предварительной записи должен вести себя как параллельный регистр. Опять нам требуется, как и при построении универсального регистра, коммутатор логических сигналов.

Напомню, что в качестве коммутатора вполне успешно используется логический элемент “2И-2ИЛИ”. Главное обеспечить подачу на элементы “И” противофазных сигналов. Это условие нам обеспечит инвертор.

Одна из схем счётчика, с возможностью параллельной записи двоичных кодов во внутренние триггеры счётчика, приведена на рисунке 13.1. В этой схеме вход C предназначен для подачи тактовых импульсов. Его ещё называют "-1", так как при подаче на этот вход импульсов, содержимое счётчика уменьшается на единицу. Входы D0 ... D3 предназначены для записи произвольного двоичного числа в счётчик. Запись производится по сигналу, подаваемому на вход параллельной записи PE.


Рисунок 13.1. Схема счётчика с возможностью параллельной записи

На первый взгляд схема достаточно сложна. Однако если приглядеться, то она состоит из одинаковых узлов. Информационные входы D триггеров могут быть подключены либо к входу параллельной записи, либо к инверсному выходу триггера. Так как в схеме применено четыре триггера, то для коммутации входов требуется четыре мультиплексора.

Точно так же переключаются источники сигналов и на тактовых входах триггеров. Входы триггеров либо подключены к выходу предыдущего триггера, либо к цепи синхронизации. Условно-графическое обозначение двоичного счётчика с возможностью параллельной записи приведено на рисунке 13.2.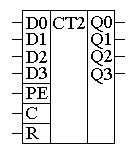

 
Рисунок 13.2. Условно-графическое обозначение счётчика с возможностью параллельной записи

Ну а теперь, точно так же как и в предыдущем примере, попробуем реализовать делитель с коэффициентом деления 1000. Вспомним, что при разработке делителя частоты сначала определяется количество микросхем двоичных счётчиков. Для этого определим степень числа 2, при которой число M=2ⁿ будет больше требуемого числа 1000.

Получаем число десять. При возведении основания системы счисления 2 в 10 степень получится число 1024. При использовании четырёхразрядных двоичных счётчиков достаточно будет трёх микросхем, так как в трёх микросхемах будет 3*4=12 триггеров, что заведомо больше минимального числа триггеров.

Следующим этапом построения делителя частоты будет перевод коэффициента деления 1000 в двоичное представление. Перевод чисел между системами счисления мы рассматривали в предыдущих главах. Десятичное число 1000₁₀ в двоичном виде будет выглядеть как 0011 1110 1000₂. Как мы уже говорили, с этого числа должен начинаться счёт вычитающего счётчика.

Схема делителя частоты на 1000 приведена на рисунке 3. В этой схеме первая микросхема является младшей, поэтому в неё загружается младшая тетрада числа предварительной записи 1000₁₀, равная 1000₂. В следующую микросхему загружается число 1110₂, а в последнюю микросхему — 0011₂.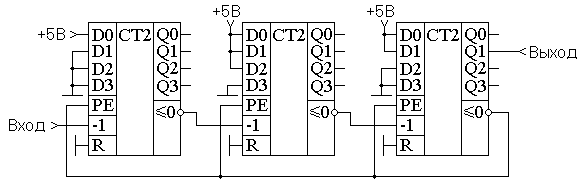

 
Рисунок 13.3 Схема делителя на 1000, построенного на основе трёх двоичных счётчиков с предварительной записью

Для определения нулевого состояния триггеров счётчика служит выход <0. Для этого внутри микросхемы расположен логический элемент "4ИЛИ". Чтобы определить обнулились ли все три микросхемы, в схеме на рисунке 3 счётные входы микросхем –1 соединяются с входом переноса предыдущей микросхемы. Как только такое состояние обнаруживается, сигнал поступает на входы параллельной записи PE, и в счётчик снова записывается число 1000.В результате работы приведённой схемы на выходе делителя импульс возникает один раз после подачи на его вход тысячи импульсов.

Обратите внимание, что на этот раз коэффициент деления заключён не в принципиальной схеме делителя, а просто подаётся на вход параллельной записи счётчиков. В результате процесс изменения коэффициента деления значительно упростился. Для изменения частоты на выходе делителя достаточно просто подать нужное число. Схема делителя, в отличие от схемы недвоичного счётчика с обратной связью, при этом не меняется.

Для построения делителя с переменным коэффициентом деления мы использовали вычитающий счётчик. Можно ли такую же схему построит на суммирующем счётчике? Можно! Однако в этом случае придётся для записи коэффициента деления воспользоваться отрицательным числом в дополнительном коде. Для того, чтобы получить отрицательное число в этом коде необходимо положительное двоичное число проинвертировать и прибавить единицу. Например, для реализации коэффициента деления 1000 возьмём его двоичный эквивалент 0011 1110 1000₂. После инвертирования получим число 1100 0001 0111₂. Окончательный результат будет равен 1100 0001 1000₂.

Для десятиразрядного двоичного кода это будет равно десятичному эквиваленту 2410. Действительно, если в счётчике с коэффициентом 2¹⁰=1024 начать считать от числа 24, то ровно через 1000₁₀ импульсов счётчик переполнится и станет равным нулю.

Глава 14

Синхронные счётчики

В рассмотренных схемах делителей частоты быстродействие всей схемы определяется временем распространения сигнала от входа до выхода самого старшего разряда. При этом получается, что чем больше требуемый коэффициент деления, тем больше двоичных разрядов счётчика требуется для реализации этого делителя. Тем большее время требуется для распространения сигнала от входа синхронизации счётчика, до его выхода, и тем меньше будет предельная частота, которую можно подавать на вход этого делителя.

Можно ли обойти такую неприятную особенность недвоичных счётчиков? Да можно! Нужно, чтобы счётчик подготавливал своё новое состояние в промежутках между тактовыми импульсами и только записывал его по приходу нового импульса.

Первая схема, которую мы рассмотрим - это схема кольцевого счётчика. Такой счётчик можно построить на основе сдвигового регистра. Схема кольцевого счётчика приведена на рисунке 14.1.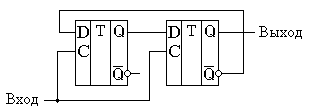



Рисунок 14.1. Схема кольцевого счетчика.

Рассмотрим работу этой схемы. Пусть первоначально в счетчике записано число 00₂. После первого же тактового импульса состояние счётчика станет равным 10₂, после второго - 11₂. Временные диаграммы этой схемы приведены на рисунке 14.2.

В результате анализа временных диаграмм можно определить, что коэффициент деления схемы кольцевого счётчика будет равен:

К_д = 2*n.

В качестве преимущества схемы кольцевого счётчика можно отметить то, что её быстродействие зависит только от времени задержки одного триггера. Это означает, что на кольцевых счётчиках можно реализовывать самые быстродействующие делители частоты.

То, что коэффициент деления пропорционален не степени количества триггеров, а только сумме является недостатком данной схемы. Это означает, что при увеличении коэффициента деления сложность схемы неоправданно возрастает по сравнению со схемой двоичного счётчика. Ещё одним недостатком схемы является то, что в результате воздействия помехи в регистр может быт записано число 01₂. В результате коэффициент деления схемы изменится, а это является недопустимым.

Ещё одним недостатком схемы кольцевого счётчика является то, что при количестве триггеров большем трёх, в результате воздействия помехи в регистр может быт записано число, содержащее несколько единиц. В результате коэффициент деления схемы изменится, а это является недопустимым. Временные диаграммы сигналов на входе и выходах 3-разрядного кольцевого счётчика при правильной и ошибочной работе приведены на рисунке 14.3.

а)

б)

Рисунок 14.3. Временные диаграммы сигналов 3-разрядного кольцевого синхронного счётчика при правильной (а) и ошибочной (б) работе.

Для того чтобы избежать неправильной работы счётчика в этот счётчик можно ввести схему контроля правильной работы. В простейшем случае это может быть обычный логический элемент “И-НЕ”. Этот элемент будет контролировать состояние счётчика, соответствующее единицам во всех его разрядах. Схема 2-разрядного счётчика со схемой проверки правильности его работы приведена на рисунке 14.4.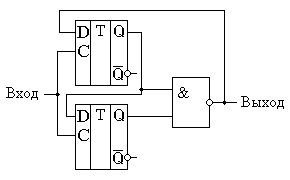



Рисунок 14.4. Схема 2-разрядного счетчика с проверкой правильности его работы.

В этой схеме триггеры счётчика при поступлении импульсов на тактовый вход  последовательно заполняются единицами. Как только все триггеры будут заполнены единицами, на выходе логического элемента “2И-НЕ” появится уровень логического нуля. При поступлении следующего тактового импульса этот ноль будет записан в первый триггер счётчика. В дальнейшем работа счётчика повторяется. Временные диаграммы сигналов на выходах этого счётчика приведены на рисунке 14.5.



Рисунок 14.5. Временные диаграммы сигналов на выходах 2-разрядного счетчика счётчика с проверкой правильности его работы.

Глава 15

Синхронные двоичные счётчики

Как мы уже упоминали ранее, основным недостатком делителей, построенных на кольцевых счётчиках, является малый коэффициент деления. Двоичные счётчики в этом смысле более эффективны. Попробуем разработать синхронный счётчик, работающий по двоичному закону. Для этого обратим внимание, что переключение следующего разряда счётчика происходит только тогда, когда состояние всех предыдущих его разрядов равно единицам. Это состояние может быть легко определено при помощи логического элемента "И".

Принципиальная схема одного из вариантов реализации четырёхразрядного синхронного двоичного счётчика приведена на рисунке 15.1.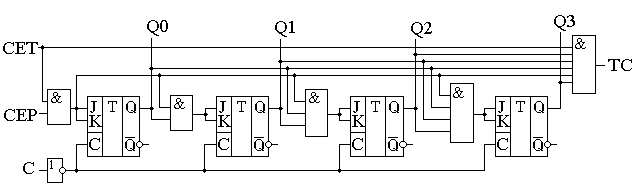

 
Рисунок 15.1. Принципиальная схема четырёхразрядного синхронного двоичного счётчика

В этой схеме счётные триггеры реализованы на основе JK триггера. В ней все триггеры переключаются одновременно, так как входной тактовый сигнал счётчика подаётся на вход синхронизации сразу всех триггеров. Разрешение переключения счётного триггера формируется схемами "И", включёнными между триггерами.

При использовании нескольких микросхем для формирования переноса, предназначенного для последующих разрядов двоичного счётчика, в приведённой схеме синхронного счётчика формируется сигнал TC. В следующих микросхемах этот сигнал подаётся на входы CEP или CET. Переключение триггеров в схеме возможно только при подаче на оба этих входа логической единицы.

В качестве примера условно-графического обозначения синхронного двоичного счётчика приведём обозначение микросхемы К1533ИЕ10.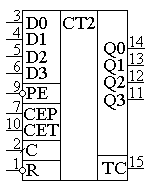

 
Рисунок 15.2. Условно-графическое обозначение синхронного счётчика с возможностью параллельной записи

Рассмотрим в качестве примера реализацию 32-х разрядного двоичного счётчика. Для этого используем четыре микросхемы К1533ИЕ10. Получившаяся принципиальная схема синхронного 32-х разрядного двоичного счётчика приведена на рисунке 7. При необходимости этот счётчик может быть легко превращён в любой недвоичный счетчик, как при помощи обратных связей, так и используя предварительную запись исходного состояния счётчика.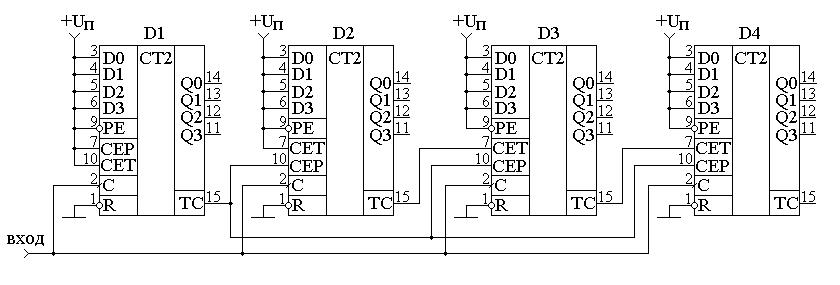


Рисунок 15.3. Принципиальная схема 32-х разрядного синхронного двоичного счётчика

Будет ли счётчик находиться в режиме счёта или в режиме параллельной записи определяется потенциалом на входах микросхем PE. При нулевом потенциале на этом входе PE производится запись информации с входов данных D во внутренние триггеры счётчиков. Именно поэтому на входы PE всех микросхем подан высокий потенциал (они подключены к источнику питания).

В схеме, приведённой на рисунке 15.3, не используются входы параллельной записи, однако мы знаем, что входы цифровых микросхем нельзя бросать в воздухе, поэтому следует присоединить их либо к источнику питания, либо к общему проводу схемы. В данной схеме все входы данных присоединены к источнику питания.

Так как в схеме на рисунке 15.3 применены микросхемы синхронных счётчиков, то все входы синхронизации должны быть соединены параллельно. Только в этом случае запись нового состояния счётчика во внутренние триггеры будет производиться одновременно.

Микросхема младших разрядов двоичного счётчика D1 должна работать всегда, пока на её вход синхронизации поступают тактовые импульсы, поэтому входы разрешения счёта CEP и CET в этой микросхеме присоединены к источнику питания. Следующая микросхема D2 должна переключиться только тогда, когда во всех триггерах микросхемы D1 будет записана логическая единица. Для этого вход разрешения счёта CEP соединён с выходом TC микросхемы младших разрядов D1. Второй вход разрешения счёта остаётся подключенным к питанию схемы.

Следующая микросхема D3 подключается так же. Однако если не принять дополнительных мер, то время распространения сигнала разрешения счёта при увеличении количества микросхем, использованных в счётчике, будет увеличиваться пропорционально количеству микросхем. Для того чтобы избежать этой ситуации, в схеме использован вспомогательный вход разрешения счёта CEP. Сигнал с выхода TC микросхемы D1 подаётся на входы CEP всех последующих разрядов.

На этом можно завершить изучение схем счётчиков, так как в особенностях внутреннего устройства и применения остальных микросхем, используя полученные знания, можно легко разобраться самостоятельно.

Раздел 7

Современные виды цифровых микросхем.

Глава 1

Микросхемы малой степени интеграции (малая логика)

В настоящее время цифровые устройства выполняются в основном с применением микроконтроллеров, сигнальных процессоров и специализированнных микросхем, таких как кодеки, модемы, аналого-цифровые или цифроаналоговые преобразователи. При этом достаточно часто возникают вопросы согласования сигналов, которыми обмениваются данные микросхемы. Иногда требуется инверсия управляющих или информационных сигналов, иногда не совсем совпадают протоколы обмена (вид сигналов записи и чтения, сигналы стробирования данных). В этом случае применение больших интегральных микросхем, таких как ПЛИС CPLD или FPGA нецелесообразно. Это либо невыгодно экономически, либо требуется большая площадь на печатной плате цифрового устройства. В то же самое время применение старых типов микросхем малой интеграции, таких как 1533 или 1564 неприемлемо либо из-за больших габаритов корпуса этих микросхем, либо несовместимости логических уровней, либо недопустимых времен распространения сигнала.

Если раньше микросхемы в основном размещали в так называемом DIP-корпусе, внешний вид которого приведен на рисунке 1.1, то в настоящее время его габариты стали недопустимо большими. Обычные габариты DIP-корпуса: 20×7,5 мм.

 
Рисунок 1.1. Внешний вид цифровой микросхемы малой степени интеграции в DIP-корпусе

В одном DIP-корпусе размещалось 6 инверторов. Но нам то обычно нужен один! И очень часто бывает, что то, что нужна инверсия сигнала выясняется уже в процессе настройки рабочего образца цифрового устройства, когда на печатной плате места практически нет. В современных цифровых микросхемах малой степени интеграции существуют корпуса микросхем, содержащие только один инвертор или только один логический элемент "2И-НЕ". В этом случае достаточно только четырех или пятивыводного корпуса и шаг выводов в современных корпусах тоже значительно уменьшился по сравнению с DIP-корпусом. Типовые габариты корпуса SOT-23 составляют 2,8×2,5 мм, габариты корпуса SС-70 составляют 2×2,1 мм, а корпуса YEP — 0,95×1,45 мм. Внешний вид корпуса SOT-23 приведен на рисунке 1.2.

 
Рисунок 1.2. Внешний вид цифровой микросхемы малой степени интеграции в SOT-23 корпусе

Подобную микросхему можно поместить в разрыв дорожки печатной платы! В качестве примера подобных микросхем можно назвать инвертор SN74LVC1G04DRL и логический элемент "2И" SN74LVC1G08DRLR фирмы texas instrument. Примеры цоколевки микросхем малой логики приведены на рисунках 3 ... 5.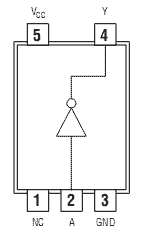

 
Рисунок 1.3. Цоколевка инвертора 1G04 в корпусе SC-70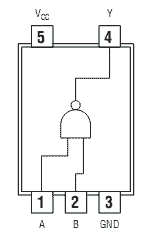 
 
Рисунок 1.4. Цоколевка логического элемента ""И-НЕ" 1G00 в корпусе SC-70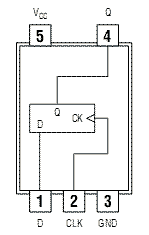 
 
Рисунок 1.5. Цоколевка D-триггера 1G79 в корпусе SC-70

Глава 2

Программируемые логические интегральные схемы (ПЛИС).

По мере развития цифровых микросхем возникло противоречие между возможной степенью интеграции и номенклатурой выпускаемых микросхем. Экономически оправдано было выпускать микросхемы средней интеграции, таких как регистры, счетчики, сумматоры. Более сложные схемы приходилось создавать из этих узлов. Разместить более сложную схему на полупроводниковом кристалле не было проблем, но это было оправдано либо очень большой серийностью аппаратуры, либо ценой аппаратуры (военная, авиационная или космическая). Заказные микросхемы не могли удовлетворить возникшую потребность в миниатюризации аппаратуры. Решение могло быть только одним — предоставить разработчикам аппаратуры возможность изменять внутреннюю структуру микросхемы (программировать).

История развития программируемых логических интегральных схем (ПЛИС) начинается с появления программируемых постоянных запоминающих устройств. Первое время программируемые ПЗУ использовались исключительно для хранения данных, однако вскоре их стали применять для реализации цифровых комбинаторных устройств с произвольной таблицей истинности. В качестве недостатка подобного решения следует отметить экспоненциальный рост сложности устройства в зависимости от количества входов. Добавление одного дополнительного входа цифрового устройства приводит к удвоению требуемого количества ячеек памяти ПЗУ. Это не позволяет реализовать многовходовые комбинационные цифровые схемы.

Для реализации цифровых комбинационных устройств с большим числом входов были разработаны программируемые логические матрицы (ПЛМ). В иностранной литературе они получили название — Programmable Logic Arrays (PLA). Именно программируемые логические матрицы можно считать первыми программируемыми логическими интегральными схемами (Programmable Logic Devices — PLDs). ПЛМ получили широкое распространение в качестве первых универсальных микросхем большой интеграции.

Классификация ПЛИС

В настоящее время программируемые логические интегральные схемы развиваются по нескольким направлениям, поэтому возникла необходимость как то различать эти микросхемы. Классификация программируемых логических интегральных схем (ПЛИС) приведена на рисунке 2.1.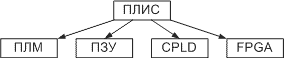

 
Рисунок 2.1. Классификация программируемых логических интегральных схем (ПЛИС)

Следует отметить, что программируемые логические матрицы (ПЛМ) реализуют хорошо известные принципы создания цифровой комбинационной схемы по таблице истинности (СДНФ). Применение постоянных запоминающих устройств (ПЗУ) в качестве комбинационной схемы позволяет вообще обойтись без составления комбинационной функции и ее минимизации. Области применения этих микросхем сразу определились. ПЗУ применялись для создания комбинационных схем с малым количеством входов. При росте количества входов сложность внутреннего устройства ПЗУ и его цена резко возрастали (по квадратичному закону). ПЛМ позволяли реализовывать таблицы истинности с относительно малым количеством единичных сигналов на выходе и большим количеством входных сигналов, либо хорошо минимизирующиеся логические функции.

Первоначально цифровые устройства с памятью реализовывали либо на нескольких ПЛМ, либо добавляли внешние триггеры, затем стали включать их в состав программируемых логических устройств. По мере увеличения степени интеграции микросхем возникла необходимость объединять полученные сложные микросхемы на одном кристалле. В результате возникли сложные программируемые логические устройства (CPLD). В них появилась возможность программировать не только таблицу истинности комбинационного устройства, но и линии соединения входов и выходов ПЛД между собой. Таким образом можно считать CPLD дальнейшим развитием ПЛМ и ПЛД.

Точно так же развивались цифровые устройства на ПЗУ. Сначала к их выходам добавили триггер. Естественно предоставили возможность отключать его при необходимости. Затем несколько этих схем разместили на одном кристалле и предоставили возможность программировать соединения их входов и выходов между собой. Подобные устройства называются FPGA.

Глава 3

Программируемые логические матрицы.

Первым представителем большого класса программируемых логических устройств (ПЛИС) стали программируемые логические матрицы (ПЛМ). В зарубежной литературе они называются PLA — Programmable logic Array. Обобщенная структура ПЛМ приведена на рисунке 3.1.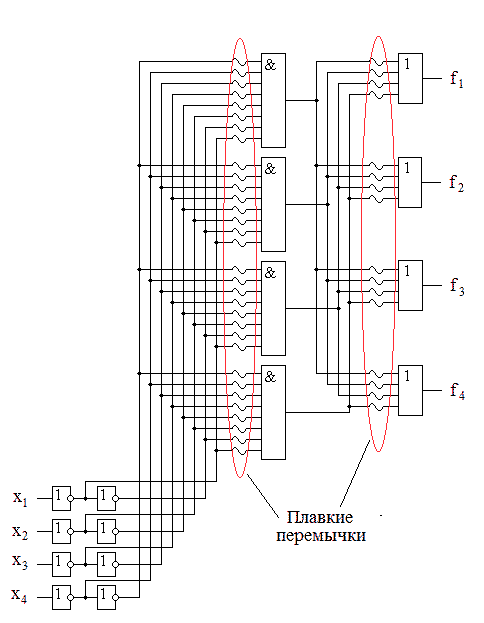

 
Рисунок 3.1. Обобщенная структура программируемых логических матриц (ПЛМ)

Основная идея работы ПЛМ заключается в реализации логической функции, представленной в СДНФ — дизъюнктивной нормальной форме. На рисунке четко прослеживаются логические элементы "И", способные реализовать любой минтерм СДНФ и логические элементы "ИЛИ", осуществляющие суммирование термов, требующихся по логическому выражению СДНФ. В схеме ПЛМ, приведенной на рисунке 3.1, ранг терма ограничен количеством входов и равен четырем, количество термов тоже равно четырем. В реально выпускавшихся микросхемах программируемых логических матриц (ПЛМ) количество входов было равно шестнадцати (максимальный ранг минтерма — 16), количество термов равно 32 и количество выходов микросхемы — 8.

Примерами реализации программируемых логических матриц могут служить отечественные микросхемы K556PT1, PT2, PT21. В этих микросхемах программирование осуществлялось при повышенном напряжении питания. Там, где требовалось сохранить плавкую перемычку на ее вход и выход подавалось высокое напряжение, там, где соединение не требовалось, на вход подавался потенциал корпуса (логический ноль), а на выход — напряжение питания. Перемычка из поликристаллического кремния под воздействием высокой температуры, вызванной током короткого замыкания, испарялась.

Следует отметить, что полная принципиальная схема ПЛМ получается достаточно громоздкой (см. рисунок 3.1). Поэтому в зарубежной литературе обычно применяется шинное представление проводников. Логический элемент "И", реализующий минтерм СДНФ, изображается как одиночная горизонтальная строка с условно-графическим обозначением схемы "И". Ко входам этого элемента подводится многоразрядная шина, а на выходе подключен одиночный проводник. Если входной проводник подключается ко входу логического элемента "И" (перемычка сохранена), то это место обозначается крестиком 'x', а если соединение отсутствует (перемычка сожжена), то крестик не проставляется. Аналогично обозначаются и многовходовые элементы "ИЛИ". Пример подобного изображения схемы ПЛМ (PLA) приведен на рисунке 3.2.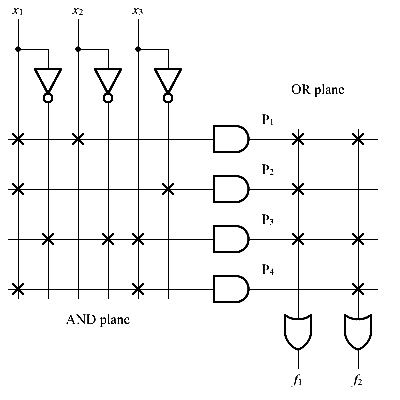

 
Рисунок 3.2. Представление внутренней структуры схем ПЛМ, принятое в зарубежной литературе

По схеме четко можно восстановить реализуемую им логическую функцию. На рисунке 3.2 реализованы две логические функции f₁ и f₂:
Недостаток рассмотренной архитектуры ПЛМ — слабое использование ресурсов программируемой матрицы логических элементов "ИЛИ". Данное обстоятельство привело к появлению ещё одного вида ПЛМ — PAL.