фывапывфпм. Цифровые интегральные микросхемы общие сведения
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
Способы наращиванияУ мультиплексоров, выпускаемых в виде самостоятельных изделий, число информационных входов не превышает шестнадцати. Большее число входов обеспечивается путем наращивания. Наращивание можно выполнять двумя способами: объединением нескольких мультиплексоров в пирамидальную (древовидную) систему либо последовательным соединением разрешающих входов и внешних логических элементов. На практике применяют оба метода. Пирамидальные мультиплексоры строятся по ступенчатому принципу, причем обычно применяются две, реже – три и более ступени. Пирамидальный характер схемы состоит в том, что каждая ступень, начиная с первой, имеет больше входов, чем последующая. Н DD1 а рис.3 показан вариант мультиплексора 321 на основе приборов 81 и 41. x0 х1 х2 х3 х4 х5 х6 х7 х8   МUX  y0      x1    А В С   DD5     А В С   x1 x2 x3 x4     y1 y2      x3 x4        D E         DD4  x24 х1 х2 х3 х4 х5 х6 х7 х8       МUX   y3    x31    А В С       Рис.3. Пирамидальный мультиплексор вида 32:1 В свою очередь, мультиплексирование шин y0 – y3 происходит при смене сигналов на адресных входах высших разрядов Е, D (микросхема DD5) от 00 до 11. Недостатками пирамидального наращивания следует считать повышенный расход микросхем, а также сравнительно невысокое быстродействие из-за суммирования задержек при последовательном прохождении сигналов по ступеням пирамиды. По функциональным возможностям мультиплексоры являются очень гибкими устройствами и помимо прямого назначения могут выполнять и другие функции. Мультиплексоры, в частности, используются для преобразования параллельного двоичного кода в последовательный. Если управляющие сигналы на адресных входах мультиплексора циклически менять в двоичной последовательности 00; 01; 10;11 и т.д. (эта операция легко выполняется с помощью двоичного счетчика), то на выходе устройства будут появляться один за другим сигналы, существующие на информационных входах, в порядке номеров этих входов. Разрядность преобразуемого слова определяется числом информационных входов. Если при этом время от времени чередовать сигналы на разрешающем входе, информация на выходе будет характеризоваться псевдослучайной последовательностью. Еще одно интересное свойство мультиплексоров – работа в качестве универсального логического элемента, реализующего любую логическую элемента, реализующего любую логическую функцию, содержащую до n +1 переменной, где n – число адресных входов мультиплексора. Применение этого свойства особенно оправданно, когда число переменных достаточно велико, 4-5 и более. Один мультиплексор в этом случае может заменить несколько корпусов с логическими элементами вида И, ИЛИ, НЕ и др. Синтез таких схем довольно прост и осуществляется на основе словесного описания функции или по таблице истинности. Использование мультиплексора в качестве универсального логического элемента основано на общем свойстве логических функций независимо от числа аргументов всегда равняться логической единице или нулю: 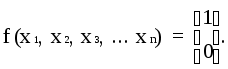 Если на адресные входы мультиплексора подавать входные переменные, зная, какой выходной уровень должен отвечать каждому сочетанию этих сигналов, то, предварительно установив на информационных входах потенциалы нуля и единицы согласно программе, получим устройство, реализующее требуемую функцию. На простом примере функции «исключающее ИЛИ» покажем, как с помощью мультиплексора 41, описанного в начале главы (см. рис.2), можно реализовать любую двоичную функцию двух переменных. Как следует из таблицы истинности для функции «исключающее ИЛИ», сочетаниям х2х1 = 00 и х2х1 = 11 отвечает значение логического 0, а двум другим х2х1 = 01 и х2х1 = 10 – логической 1. Для выполнения этих условий достаточно подключить к адресным входам мультиплексора А и В шины сигналов х1 и х2 соответственно, на информационные входы D0 и D3 подать потенциал логического 0, а на D1 и D2 – логической 1. Разрешающий вход при этом должен быть в состоянии логического 0 (рис.4). Если число аргументов равно n +1, то мультиплексор следует включать несколько иначе. Допустим, что на основе того же мультиплексора (по рис.2) требуется составить схему, реализующую функцию трех переменных, заданную таблицей истинности 2 12. Таблица 2
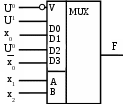 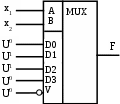 Рис.4 Рис.5. Схемная реализация функции, представленной табл.2 Расчленим мысленно таблицу истинности на группы по две строки в каждой; в каждой группе х2 и х1 неизменны, х0 (аргумент младшего разряда) имеет два состояния, а выходной сигнал F может иметь одно из четырех значений: F = 1; F = 0; F = х0 и F = х0. Если переменные сигналы х2 и х1 подключить к адресным входам мультиплексора В и А, а на информационные входы D0 – D3 подать согласно таблице истинности постоянные потенциалы U1, U0 и переменные сигналы х0, то такая схема (рис.5) будет удовлетворять заданным условиям. Описанный метод проектирования годится также для составления схем и с большим числом переменных. На рис.6 показана матрица информационных и адресных шин при четырех входных переменных. Конкретные точки соединений шин определяются по заданной таблице истинности. Рис.6. Матрица информационных и адресных шин для четырех переменных В  гл. 9 (см рис. 9-18 и 9-19) показаны способы применения мультиплексоров в качестве сумматоров. гл. 9 (см рис. 9-18 и 9-19) показаны способы применения мультиплексоров в качестве сумматоров. |
