|
|
Действия над комплексными числами. Действия над комплексными числами в алгебраической форме. Действия над комплексными числами в алгебраической форме
ГККП «Колледж сервиса и новых технологий»
УО ЗКО
Тема занятия: Действия над комплексными числами в алгебраической форме.
Наименование модуля /дисциплины: Математика
Подготовил педагог: Андрусенко Н.А.
"31" марта 2023 года
1. Общие сведения
Курс, группы: 1 курс; №192, №112, №122
Тип занятия: комбинированный урок.
2. Цели, задачи
научить выполнять различные операции над комплексными числами в алгебраической форме;
развивать у студентов логическое мышление, умение обобщать полученные знания, проводить анализ и сравнение, приводить примеры и делать необходимые выводы; воспитывать интерес к изучению математики, математическую культуру и речь; способствовать воспитанию высокой творческой активности.
Уровень мыслительных навыков: Знание и понимание, применение.
3. Ожидаемые результаты: учащиеся должны: знать: определение суммы, разности, произведения и частного комплексных чисел.
Уметь: выполнять различные операции над комплексными числами в алгебраической форме.
4. Необходимые ресурсы:
Учебник Алгебра и начала анализа для 11 класса общеобразовательной школы естественно-математического направления общеобразовательных школ. Авторы: А.Е. Абылкасымова, В.Е. Корчевский, З.А. Жумагулова
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
https://www.youtube.com/watch?v=KjeGbQmMV5Q
Презентация
5. Ход урока.
Запланированные этапы урока
|
Деятельность, запланированная на уроке
|
Ресурсы
|
Начало урока
|
Приветствие. Определение отсутствующих. Настрой на работу.
Повторение
- Что такое «комплексное число»
- чему равен квадрат мнимой «1»
- какие числа называются сопряженными
- Какие комплексные числа называются равными
- Какие комплексные числа называются противоположными
- что такое модуль комплексного числа
|
Презентация
|
Середина урока
|
Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.
Определение. Суммой комплексных чисел z1 = a1 + b1 i и z2 = a2 + b2i называется комплексное число z, действительная часть которого равна сумме действительных частей z1 и z2, а мнимая часть - сумме мнимых частей чисел z1 и z2, то есть z = (a1 + a2) + (b1 + b2) i.
Числа z1 и z2 называются слагаемыми.
Сложение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z1 + z2 = z2 + z1.
2º. Ассоциативность: (z1 + z2) + z3 = z1 + (z2 + z3).
3º. Комплексное число – a – bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0
Пример 1. Выполните сложение (3 – i) + (-1 + 2i).
(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
Самостоятельно: Сложить два комплексных числа Z1=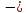 4+10i и Z2=6+7i Ответ: Z=2+17i 4+10i и Z2=6+7i Ответ: Z=2+17i
2) Вычитание.
Определение. Вычесть из комплексного числа z1 комплексное число z2, значит найти такое комплексное число z, что z + z2 =z1.
Теорема. Разность комплексных чисел существует и притом единственная.
Пример 2. Выполните вычитание (4 – 2i) - (-3 + 2i).
(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.
Самостоятельно: Найти разности комплексных чисел Z1=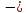 5+10i и Z2=1+3i Ответ: Z= 5+10i и Z2=1+3i Ответ: Z=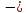 6+7i 6+7i
3) Умножение.
Определение. Произведением комплексных чисел z1=a1+ b1 i и z2=a2+b2i называется комплексное число z, определяемое равенством:
z = (a1 a2 – b1b2) + (a1b2 + a2b1) i.
Числа z1 и z2 называются сомножителями.
Умножение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z1z2 = z2 z1.
2º. Ассоциативность: (z1z2)z3 = z1 (z2z3)
3º. Дистрибутивность умножения относительно сложения:
(z1 + z2) z3 = z1z3 + z2z3.
4º. z · 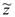 = (a + bi) (a – bi) = a2 + b2 - действительное число. = (a + bi) (a – bi) = a2 + b2 - действительное число.
На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.
В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.
Пример 3. Выполните умножение (2 + 3i) (5 – 7i).
1 способ. (2 + 3i) (5 – 7i) = (2⋅ 5 – 3⋅ (- 7)) + (2⋅ (- 7) + 3⋅ 5)i =
= (10 + 21) + (- 14 + 15)i = 31 + i.
2 способ. (2 + 3i) (5 – 7i) = 2⋅ 5 + 2⋅ (- 7i) + 3i⋅ 5 + 3i⋅ (- 7i) =
= 10 – 14i + 15i + 21 = 31 + i.
Самостоятельно: Найти произведение комплексных чисел
1) Z1=5-2i и Z2=1-4i Ответ: Z= -3 - 22i
2) ( 2+ 8i )( 2 – 8i ) = 2 2 + 82
Вывод: ( a+ bi )( a – bi )= a 2 + b 2. Следовательно, произведение двух сопряжённых комплексных чисел равно действительному положительному числу.
4) Деление.
Определение. Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1.
Теорема. Частное комплексных чисел существует и единственно, если z2 ≠ 0 + 0i.
На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.
Пусть z1 = a1 + b1i, z2 = a2 + b2i, тогда 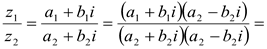
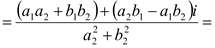
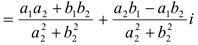
В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.
Пример 4. Найти частное
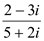
1 способ.
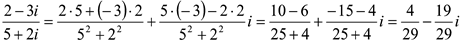
2 способ.
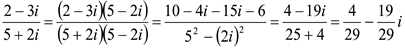
5) Возведение в целую положительную степень.
а) Степени мнимой единицы.
Степени in, где n – целое положительное число, периодически повторяется при увеличении показателя на 4 .
Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.
Пример 5. Вычислите: (i 36 + i 17) · i 23.
i 36 = (i 4) 9 = 1 9 = 1,
i 17 = i 4⋅ 4+1 = (i 4)4⋅ i = 1 · i = i.
i 23 = i 4⋅ 5+3 = (i 4)5⋅ i3 = 1 · i3 = - i.
(i 36 + i 17) · i 23 = (1 + i) (- i) = - i + 1= 1 – i.
б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.
Пример 6. Вычислите: (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3⋅ 42⋅ 2i + 3⋅ 4⋅ (2i)2 + (2i)3 = 64 + 96i – 48 – 8i = 16 + 88i.
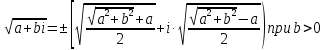
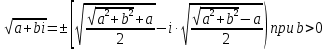
Пример 7. Найдем значение корня 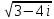 . .
Решение. a = 3, b = - 4. Воспользуемся полученной формулой и найдем:
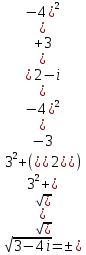 , ,
или 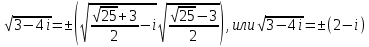
Ответ: 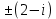 . .
|
https://www.youtube.com/watch?v=KjeGbQmMV5Q
Презентация
Презентация
Презентация
|
Конец урока
|
Задание.(по 10%)
1. Сложить два комплексных числа:
а) Z1 = 2+5i и Z2=4-3i.
б) Z1 = -4+10i и Z2=5+3i.
в) (2 + 3i)+ (5 – 7i).
2. Найти разности комплексных чисел
а) Z1=10-25i и Z2=1-3i.
б) Z1=-5+10i и Z2=1+3i.
3.Выполнить деление:
а)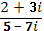
б) (5 + 3i):(1 - 2i)
4.Выполнить умножение:
а) (5 + 3i)(5 – 3i);
б) (2 + 5i)(2 – 5i);
в) (1 + i)(1 – i).
Дескриптор: Обучающийся
- выполняет арифметические операции над комплексными числами;
- вычисляет значение выражения.
Рефлексия.
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Д/з Гл.5, §17
|
Учебник Алгебра и начала анализа для 11 класса
Презентация
| |
|
|
 Скачать 66.95 Kb.
Скачать 66.95 Kb.
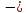 4+10i и Z2=6+7i Ответ: Z=2+17i
4+10i и Z2=6+7i Ответ: Z=2+17i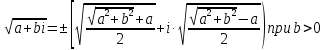
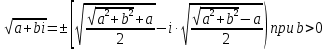
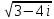 .
.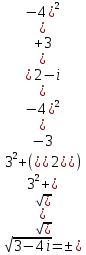 ,
,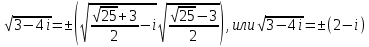
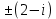 .
.