Дипломная работа функциональные уравнения на оси и полуоси содержание введение
 Скачать 3.15 Mb. Скачать 3.15 Mb.
|
|
6. Некоторые обобщения и приложения 6.1 Функциональная характеристика тригонометрического и гиперболического косинусов Если f(x) = cos ax или ch ax (a ≥ 0) (6.1) то, при любых вещественных значениях x и y,удовлетворяется соотношение f(y+x)+f(y-x)=2f(x)∙f(y) (6.2) Это с легкостью вытекает из теоремы сложения для обоих косинусов: 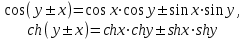 (6.3) (6.3)Функциональное уравнение (6.2) вместе с требованием непрерывности функции, и на этот раз полностью характеризует оба косинуса: Единственными функциями, определенными и непрерывными в промежутке (-∞, +∞) и удовлетворяющими в нем уравнению (6.2), являются тригонометрический и гиперболический косинусы (6.1) (если, не считать функции, тождественно равной нулю). ►Итак, пусть f(x) будет непрерывная для всехx функция, удовлетворяющая условию (6.2). Полагая x=0и принимая за у какое либо из значений, для которого f(y)≠0, заключаем, что f(0)=1. (6.4) При y=0 в таком случае получается f(-x)=f(x) (6.5) так что функция f(x) оказывается четной. Поскольку непрерывная функция f(x) при x=0 будет положительна, то найдется такое, скажем, положительное число с, что f(x) будет положительна на всем промежутке [0,c]. В дальнейшем исследование пойдет по разным путям, в зависимости от того, будет ли а) f(c) ≤ 1 или б) f(c) > 1. Займемся случаем а). Так как 0 < f(c) ≤ 1, то найдется такое θ 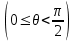 , что , что f(c) = cos θ. (6.6) Приведя затем основное соотношение (6.2) к виду : f(y +x) = 2 f(x)∙f(y) - f(y - x), станем в нем последовательно полагать 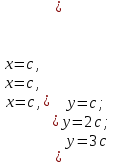 и т.д. Мы получим (с учетом (6.4) и (6.6)) 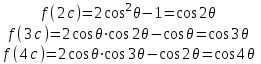 и т.д. Пользуясь методом математической индукции, легко докажем для любого натурального m формулу f(mc)=cosmθ(6.7) если же в (6.2) положить 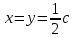 , то получим (снова с учетом (6.4) и (6.6)): , то получим (снова с учетом (6.4) и (6.6)):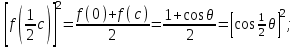 так как f(x) остается положительной между 0 и с, а функция cos x - между 0 и θ, то, извлекая положительные корни в обеих частях, придем к равенству: 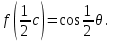 совершенно также, полагая в (6.2) x=y= 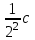 , найдем , что , найдем , что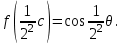 и т.д. Так, последовательно (математическая индукция!), получим и общее соотношение 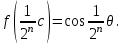 (n=1, 2,3,…) (6.8) (n=1, 2,3,…) (6.8)Наконец, повторяя тот процесс, с помощью которого мы, отправляясь от (6.6) к (6.7), мы из (6.8) придем к равенству: 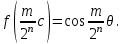 Итак, для положительных значений x вида 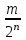 имеем: имеем:f(cx) =cos θx (6.9) Но так как любое положительное число x можно представить как предел значений этого вида, то, с помощью предельного перехода (и опираясь на непрерывность функций f(x) и cos(x)), установим справедливость формулы (6.9) для всех x>0. Для x<0 она будет верна в силу (6.5), а для x=0 - в силу (6.4). Если заменить в (6.9) x на 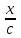 и положить и положить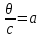 , то и получим окончательно: , то и получим окончательно:f(x)=cosax. В случае б) имеем: f(c)>1; тогда найдется такое θ, что f(c) = chθ. Повторяя дословно все проведенные только что рассуждения и опираясь на соотношения для гиперболического косинуса, совпадающие по форме с соответствующими соотношениями для тригонометрического косинуса, мы для рассматриваемого случая найдем, что f(x)=chax. (a>0) При a=0, по обеим формулам получили бы: f(x)≡1.▲ 6.2 Решение уравнения для синуса на оси R Наряду с уравнением (6.2), определяющим функции cosax и сhax, рассмотрим дифференциальное функциональное уравнение f′(x - y)-f′(x + y)=2λf(x)∙f(y) λ≠0 (6.10) и покажем, что при дополнительном требовании дважды дифференцируемости f(x) оно характеризует функции С sin αxи С sh αx(если не считать функции, тождественно равной 0) ► 1. при у=0, имеем 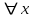 , f′( x)-f′(x)=2λf(x)∙f(0)=0 , f′( x)-f′(x)=2λf(x)∙f(0)=0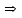 f(0)=0 (6.11) f(0)=0 (6.11)2. при х=0, имеем 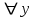 , f′(-у)-f′(у)=2λf(0)∙f(у)=0 , f′(-у)-f′(у)=2λf(0)∙f(у)=0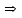 f′(х)-четная f′(х)-четная . продифференцируем (6.10) по у: -f′′(x-y)-f′′(x+y)=2λf(x)∙f′(y) при у=0 имеем -2f′′(x)=2λf(x)∙f′(0) f′(0)=с f′′(x)+λ∙с∙f(x)=0 f(0)=0 f′(0)=с для λ>0, будем рассматривать случаи, когда с=0, с<0, c>0 a) c=0: f′′(x)=0 f′′(x)=C1x+C2 f(0)=f′(0)=0 C1=C2=0. f(x)≡0 b) c<0: f(x)= 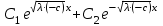 (0)=C1+C2=0 (0)=C1+C2=0C1=-C2 f(x)= 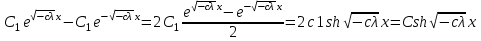 ′(x)= ′(x)=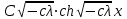 ′(0)= ′(0)=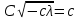 = =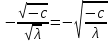 (x)= (x)=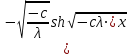 ; ;положив α= 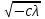 f(x)= 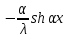 =-β sh λβx ; =-β sh λβx ; b) c > 0: f(x)= 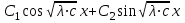 (0)=C1 =0 (0)=C1 =0f(x)= 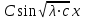 ′(x)= ′(x)=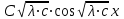 ′(0)= ′(0)=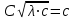 C= 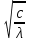 f(x)= 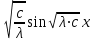 ; ;положив α= 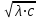 f(x)= 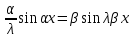 , ▲ , ▲6.3 Класс уравнений типа Коши Сделаем далее еще одно обобщение. Классические функциональные уравнения Коши [8] f(x+y)=f(x)+f(y), f(x+y)=f(x)∙f(y), f(x∙y)=f(x)+f(y), f(x∙y)=f(x)∙f(y), имеющие непрерывные решения соответственно с∙x, 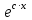 , с∙lnx, xс, связывают основные смежные (в смысле распределительного закона) арифметические операции сложения + и умножения ∙ . , с∙lnx, xс, связывают основные смежные (в смысле распределительного закона) арифметические операции сложения + и умножения ∙ . В [9] указаны примыкающие к ним: «снизу» - операция x 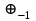 y = ln(ex+ey), «сверху» - операция x y = ln(ex+ey), «сверху» - операция x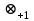 y=e(lnx∙lny). Все эти операции являются звеньями «естественной цепи арифметических операций» y=e(lnx∙lny). Все эти операции являются звеньями «естественной цепи арифметических операций» 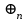 [10], в которой += [10], в которой +=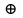 0, ∙ = 0, ∙ =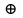 +1, так что +1, так что 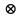 +1= +1=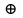 +2 (и вообще +2 (и вообще 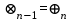 ). Их связывает класс функциональных уравнений типа Коши (название указывает на связь различных арифметических операций) ). Их связывает класс функциональных уравнений типа Коши (название указывает на связь различных арифметических операций)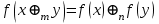 где m,n - целые числа. Решения некоторых уравнений (с малыми индексами) таковы:
Наблюдающиеся здесь закономерности справедливы в общем случае.[7] Заключение В данной дипломной работе, посвященной решению некоторых функциональных уравнений на оси, был рассмотрен важнейший класс уравнений - класс уравнений Коши. Были приведены некоторые методы решения функциональных уравнений, с помощью которых впоследствии были решены важнейшие функциональные уравнения элементарной математики, f(x+у) = f (x) + f (y), f (x + у) = f (x) f (y), f (xy) = f (x) + (y),(xy) = f (x) f (y), показано, что найденные решения могут служить для определения функции f(x)=Cx, а также показательной, логарифмической, степенной функций. Утверждения были сформулированы в виде теорем для функций, определенных на Q, функций непрерывных на R и R+, а также для любых измеримых функций. Все теоремы были доказаны и сделан вывод о том что решения имеют один и тот же вид для функций, определенных на Q, функций непрерывных на R и R+, а также для любых измеримых функций. Были решены уравнения, определяющие функции тригонометрический и гиперболический косинус. Также решено уравнение f′(x-y)-f′(x+y)=2λf(x)∙f(y), решения которого имеют вид f(x)=-βshλβx, , и f(x)=βsinλβx. Было приведено также важное обобщение свойств уравнений типа Коши и сделан вывод: Список использованных источников 1. Энциклопедия элементарной математики. Т.3. Под ред. П.С. Александрова, А.И. Маркушевича, А.Я. Хинчина. Государственное издательство технико-теоретической литературы. М.: 1952.-560 с. . Функциональные уравнения. Квант, 1985.-- № 7. . Прасолов, В. В. Задачи по алгебре, арифметике и анализу. М.: МЦНМО, 2005. - 545 с. . Фихтенгольц, Г. М., Курс дифференциального и интегрального исчисления. Т.1. М. : Наука, 1970.-616 с. . Колмогоров, А. Н., Фомин, С. В. Элементы теории функций и функционального анализа. М.: Физматлит, 2006. - 572 с. . Сенета, Е. Правильно меняющиеся функции. М. : Наука, 1985.-143 с. . Блюмин, С. Л. Класс уравнений типа Коши / Научный журнал "Фундаментальные исследования"// Российская Академия Естествознания [Электронный ресурс]. - Электрон. журн. - 2008. - №2 - Режим доступа: http://www.rae.ru . Нечепуренко, М. И. Итерации вещественных функций и функциональные уравнения. - Новосибирск: ИВМиМГ СО РАН, 1997.- 228 c. 9. Арнольд, И. В. Теоретическая арифметика. - М.: ГУПИ, 1938. - 480 с. 10. Carroll, M. The Natural Chain of Binary Arithmetic Operations and Generalized Derivatives [arXiv.org/math.HO/0112050] Все о написании дипломных работ на сайте https://edunews.ru/students/vypusknaya/ |

