Дипломная работа функциональные уравнения на оси и полуоси содержание введение
 Скачать 3.15 Mb. Скачать 3.15 Mb.
|
|
Например, функциональное уравнение f (x) = f (-x) характеризует класс чётных функций, функциональное уравнение f(-x) = -f(x) - класс нечетных; функциональное уравнение f (x + 1) = f (x) - класс функций, имеющих период 1, и т.д. Одним из простейших функциональных уравнений является уравнение f (x + у) = f (x) + f (y). Непрерывные решения этого функционального уравнения имеют вид: f (x) = Cx. Однако в классе разрывных функций это функциональное уравнение имеет и иные решения. С рассмотренным функциональным уравнением связаны f (x + у) = f (x) f (y),(xy) = f (x) + f (y),(xy) = f (x) f (y), непрерывные решения которых имеют соответственно вид eCx, Т.о., эти функциональные уравнения могут служить для определения показательной, логарифмической и степенной функций. В теории аналитических функций Например, двоякопериодические функции характеризуются функциональными уравнениями: f (z + а) = f (z) и f (z + b) = f (z), автоморфные функции f (saz) = f (z), где {sa} - некоторая группа дробно-линейных преобразований. Если функция известна в некоторой области, то знание для неё функционального уравнения позволяет расширить область определения этой функции. Например, функциональное уравнение f (x + 1) = f (x) для периодических функций позволяет определить их значение в любой точке по значениям на отрезке [0, 1]. Этим часто пользуются для аналитического продолжения функций комплексного переменного. Например, пользуясь функциональным уравнением Г (z + 1) = z∙Г (z) и зная значения гамма-функции Г(z) в полосе 0 < Re Условия симметрии, имеющиеся в какой-либо физической задаче, обусловливают определённые законы преобразования решений этой задачи при тех или иных преобразованиях координат. Этим определяются функциональные уравнения, которым должно удовлетворять решение данной задачи. Значение соответствующих функциональных уравнений во многих случаях облегчает нахождение решений. Решения функциональных уравнений могут быть как конкретными функциями, так и классами функций, зависящими от произвольных параметров или произвольных функций. Для некоторых функциональных уравненийобщее решение может быть найдено, если известны одно или несколько его частных решений. Например, общее решение функционального уравнения f (x) = f (ax) имеет вид j(w(x)), где j(x) - произвольная функция, а w(x) - частное решение этого функционального уравнения Для решения функциональных уравнений их во многих случаях сводят к дифференциальным уравнениям. Этот метод даёт лишь решения, принадлежащие классу дифференцируемых функций. Другим методом решения функциональных уравнений является метод итераций f [a(x)] = f (x) + 1, где a(x) - заданная функция и связанного с ним уравнения Шрёдера: f [a(x)] = c f (x). А. Н. Коркин 1.2 Методы решения функциональных уравнений Методы решения - методы нахождения точных или приближенных решений функциональных конкретных или абстрактных уравнений, т.е. уравнения вида P(x)=y, (1.1) Где P(x) - некоторый, вообще говоря нелинейный оператор, переводящий элементы пространства X типа В (или другого типа) в элементы пространства Y того же типа. Точные решения в виде аналитических выражений получаются лишь для немногих типов функциональных уравнений, поэтому особое значение имеют приближенные методы решения. Для нахождения решений общих функциональных уравнений развит ряд методов, например, метод бесконечных степенных рядов, метод последовательных приближений, метод Галеркина (метод моментов), метод касательных гипербол, метод Чебышева (касательных парабол), метод Ньютона-Канторовича и его модификации, метод наискорейшего спуска и др., а также методы вариации параметра (прямые, итерационные и комбинированные) определенных типов и их различные модификации, в том числе и с последовательной аппроксимацией обратного оператора. Общие методы применяются к решению различных конкретных функциональных уравнений математического анализа. Кроме того, существуют специальные методы решения конкретных функциональных уравнений, в том числе и численные методы, например, метод сеток и др. Метод вариации параметра, метод Ньютона-Канторовича и некоторые другие из указанных методов имеют также и теоретическое значение, так как с их помощью можно делать заключение о существовании, единственности и области расположения решения функционального уравнения, не находя самого решения, что подчас не менее важно, чем фактическое значение решения. Ниже рассмотрим несколько методов решения. a) Метод подстановок: Пусть, например, имеется функциональное уравнение: f (x + y) + f (x - y)=2∙f (x)∙cos y (1.2) Применяя последовательно подстановки x=0, y=t; x= 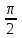 +t, y= +t, y=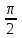 ; x= ; x=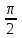 , y= , y=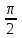 +t, +t, из (1.2) получают соответственно уравнения f(t) + f(-t) = 2acost, f(π + t) + f(t )= 0 и f(π + t) + f(-t)= 2b cos( 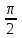 + t) = -2b sin t, + t) = -2b sin t,где обозначено f(0) = a, f( 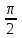 ) = b. Отсюда путем вычитания из суммы первых двух уравнений третьего, получают 2 f(t)=2acost + 2bsint. Общим решением исходного функционального уравнения (1.2) является функция f(x)=a cos x + и sin x. Этот метод применим также и к другим уравнениям типа ) = b. Отсюда путем вычитания из суммы первых двух уравнений третьего, получают 2 f(t)=2acost + 2bsint. Общим решением исходного функционального уравнения (1.2) является функция f(x)=a cos x + и sin x. Этот метод применим также и к другим уравнениям типаH [ f(x + y), f(x - y), f(x), x, y ] = 0 при некоторых предположениях относительно функции Н. К уравнениям других типов применяются различные другие подстановки. Метод подстановок применяется и для сведения одних функциональных уравнений к другим уравнениям того же типа, в частности к функциональным уравнениям с известными решениями. Например, функциональное уравнение f((x + y)/2) = f(x)/2 + f(y)/2 (1.3) может быть приведено к функциональному уравнению Коши f (x + y) = f(x) + f(y) (1.4) с непрерывным решением f(x)=Cx. С этой целью в (1.3) подставляют x+y вместо х и 0 вместо у: f((x + y)/2) = f(x +у)/2 + а/2 , где a=f(0) Сравниваяэто с исходным функциональным уравнением (1.3) получают функциональное уравнение вида f (x + y) = f(x) + f(y) - а, откуда φ(x+y)= φ(x)+ φ(y), φ(x)=f(x)-a и φ(x) = Сх. Решением являетсяфункция f(x) = Cx+a. Для сведения к другим функциональным уравнениям того же типа применяют также логарифмирование и другие приемы. Например, решение функционального уравнения f (x + y) = f (x) ∙ f (y) (1.5) путем логарифмирования можно свести к решению уравнения (1.4). b) Метод замены переменной: Для того чтобы проиллюстрировать этот метод рассмотрим уравнение: 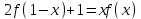 (1.6) (1.6)Предположим, что существует функция f(x), удовлетворяющая данному уравнению. Заменив x на 1-x, получим 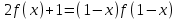 Из (1.6) находим 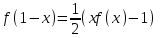 . Подставляя значение во второе уравнение, получим: . Подставляя значение во второе уравнение, получим: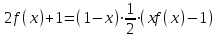 откуда откуда 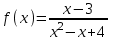 В рассмотренном уравнении под знаком уравнении под знаком неизвестной функции стоят функции f1=x и f2=1-x. Замена x на 1-x переводит функции f1 и f2 друг в друга. В результате замены переменной получено еще одно уравнение, содержащие f(x) и f(1-x). Решение функционального уравнения сводится к решению системы двух линейных уравнений с двумя неизвестными. Рассмотрим еще одно уравнение: 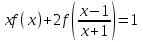 (1.7) (1.7)Выполним замену х→ 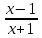 , получаем , получаем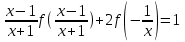 (1.8) (1.8) появилось новое «неизвестное» выражение 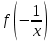 . Применим еще одну подстановку: . Применим еще одну подстановку:  , имеем , имеем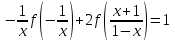 (1.9) (1.9)Кроме 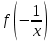 , в уравнении появилось «нежелательное» выражение , в уравнении появилось «нежелательное» выражение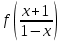 , выполним в (1.7) подстановку , выполним в (1.7) подстановку 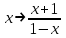 . И получаем уравнение . И получаем уравнение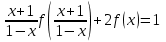 (1.10) (1.10)построена система линейных уравнений (1.7)-(1.10) с четырьмя неизвестными 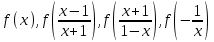 . Последовательно исключая переменные, получим . Последовательно исключая переменные, получим 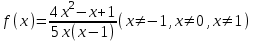 . .c) Метод решения функциональных уравнений с помощью понятия группы Пусть в функциональном уравнении a1f(g1)+a2f(g2)+…+anf(gn)=b (1.11) выражения, стоящие под знаком неизвестной функции f(x) являются элементами группы G, состоящей из n функций: g1(x)=x, g2(x),…gn(x), причем коэффициенты уравнения (1.11) a1, a2, …an, b - некоторые функции от x. Предположим, что уравнение (1.11) имеет решение. Заменим x→g2(x). В результате последовательность функций g1(x), g2(x),…gn(x), перейдет в последовательностьg1º g2, g2º g2,…gnº g2, состоящую из всех элементов группы. Поэтому «неизвестные» f(g1), f(g2),… f(gn), переставятся и мы получим новое линейное уравнение того же вида, что и (1.11), далее заменим x→g3(x),…x→gn(x), после чего получим систему из n линейных уравнений, которую следует решить. Если решения есть, то проверкой нужно убедиться в том, что они удовлетворяют уравнению. Группой называется множество G функций, обладающее следующими свойствами: 1. Для любых двух функций 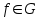 и и 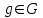 их композиция их композиция 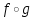 также принадлежит G. также принадлежит G.. Функция e(x)=x принадлежит G. . Для всякой функции 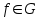 существует обратная функция f-1, которая также принадлежит G. существует обратная функция f-1, которая также принадлежит G.Из важных методов решения функциональных и функционально-дифференциальных уравнений следует отметить также метод дифференцирования |
