4.02 дисперсия электронов. 4.02 - Дисперсионная и разреш. способность призмы и дифракц. Дисперсионная и разрешающая способность призмы и дифракционного спектрометра Цель работы
 Скачать 0.75 Mb.
|
|
3. Дифракционные спектральные приборы. В основе действия дифракционных спектральных приборов лежит явление дифракции. За краткой теорией дифракции можно обратиться к лабораторной работе № . В данной работе остановимся только на особенностях и характеристиках дифракционного спектра, получаемого с помощью дифракционной решетки. Дифракционной решеткой называется оптический элемент с периодической структурой, представляющей собой чередование, например, параллельных щелей и непрозрачных промежутков. Наблюдаемый на таких структурах дифракционный спектр есть результат многолучевой интерференции дифрагированного сложного излучения, получаемой методом деления фронта волны. Здесь число щелей соответствует числу когерентных источников. Число щелей может быть очень большим (до 2400 на 1мм). Такая решетка периодически меняет амплитуду проходящих через нее световых волн и поэтому называется амплитудной (есть фазовые решетки – эшелон Майкельсона, эшелетт Вуда). Как показано на рис. 3, при освещении решетки параллельным пучком световых лучей (плоская волна) каждая ее щель, в соответствии с принципом Гюйгенса-Френеля, становится самостоятельным источником когерентных световых волн (лучей), расходящихся по всевозможным направлениям. Если за решеткой поставить собирающую линзу Л, то она отсортирует дифрагированные лучи по направлениям: лучи одного направления соберутся в одной точке фокальной плоскости линзы на экране Э и будут интерферировать друг с другом. Максимум интерференции дифрагированного монохроматического света от решетки наблюдается, когда оптическая разность хода волн, приходящих от двух соседних щелей равна либо нулю, либо целому числу длин волн:   , (30)где  - оптическая разность хода лучей от двух соседних щелей решетки,  - длина волны монохроматического света,  - угол, соответствующий максимуму интерференции или дифракционному максимуму,  - порядок дифракционного максимума.INCLUDEPICTURE "C:\\Documents and Settings\\Администратор\\Рабочий стол\\makogina\\media\\image2.jpeg" \* MERGEFORMATINET 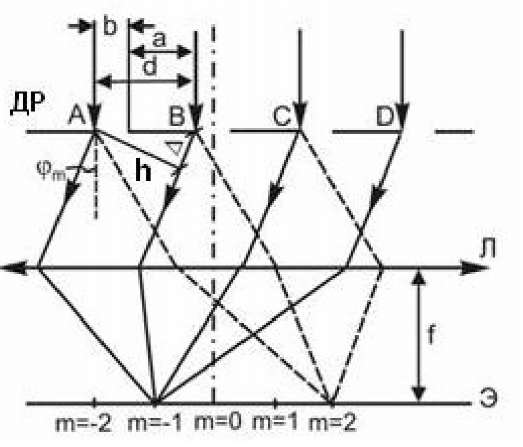 Рис. 3. Формирование дифракционной картины: ДР – амплитудная дифракционная решетка,  - ширина непрозрачного промежутка,  - ширина щели,  - период решетки, = угол дифракции, - разность хода световых волн,  - ширина дифрагированного пучка,  - фокусное расстояние линзы Л, Э – экран, - порядок спектра.Формула (30) называется формулой дифракционной решетки, или условием главных максимумов дифракционной картины. Линза не вносит дополнительной разности хода лучей. Число, равное числу длин волн, укладывающихся на оптической разности хода и образующих данный максимум, называется порядком дифракционной картины .Так как угловое положение максимума дифракционной картины, согласно формуле (30), зависит от длины волны , то в случае немонохроматического излучения максимумам дифракционной картины разного порядка соответствуют ярко освещенные линии определенного цвета на темном фоне.Пример схематического изображения дифракционного спектра, даваемого немонохроматическим источником света, приведен на рис. 4а. Угловую дисперсию дифракционной решетки можно рассчитать, воспользовавшись определением и формулой (1). Продифференцировав выражение (30) слева по углу  , справа по длине волны , получаем  , откуда . (31)Если углы, под которыми наблюдаются дифракционные максимумы, невелики  , то  при всех , тогда (32)INCLUDEPICTURE "C:\\Documents and Settings\\Администратор\\Рабочий стол\\makogina\\media\\image3.jpeg" \* MERGEFORMATINET 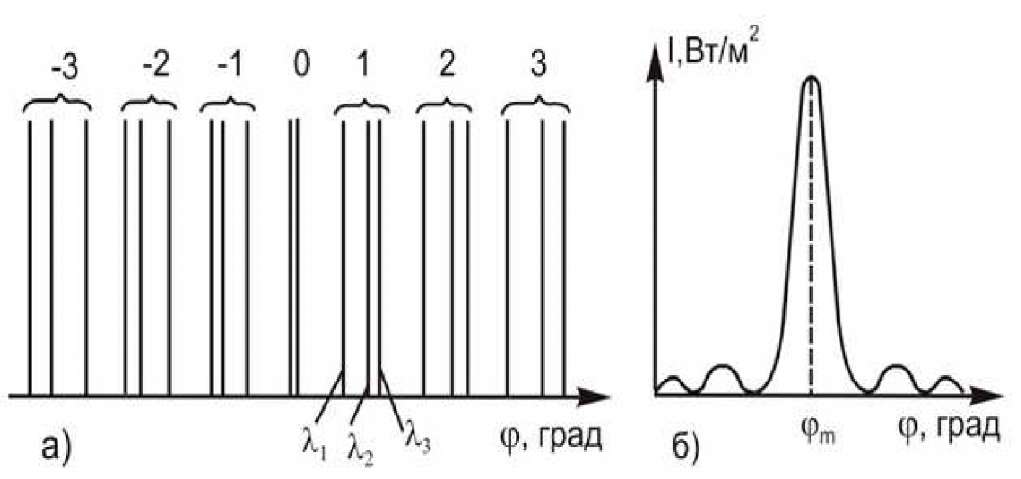 Рис 4. Схематическое изображение дифракционного спектра немонохроматического источника, излучение которого содержит три монохроматические составляющие в области видимого света (а) и распределение интенсивности в одной из спектральных составляющих (б). Очевидно, что величина дисперсии пропорциональна порядку спектра для данной решетки, и чем меньше ее период, тем больше дисперсия в определенном порядке. Теоретическую разрешающую способность дифракционной решетки можно получит из формулы (5), приняв во внимание, что ширина параллельного пучка, дифрагировавшего под углом , для решетки из  штрихов, есть:  (рис.3). Тогда с учетом формулы (31) . (33)Максимальное значение  будет в спектре наибольшего порядка, который возможен при заданных значениях периода  и длины волны .4. Описание экспериментальной установки. Общий вид установки представлен на рис.5. INCLUDEPICTURE "C:\\Documents and Settings\\Администратор\\Рабочий стол\\makogina\\media\\image6.jpeg" \* MERGEFORMATINET  Рис. 5. Общий вид экспериментальной установки. В состав установки входят: ртутная лампа 1, блок питания 2, спектрометр-гониометр 3, набор призм и дифракционных решеток 4. Наблюдение спектров и отсчет углов производится с помощью спектрометра-гониометра, схема которого изображена на рис. 6., а примерный ход лучей – на рис.7. INCLUDEPICTURE "C:\\Documents and Settings\\Администратор\\Рабочий стол\\makogina\\media\\image7.jpeg" \* MERGEFORMATINET 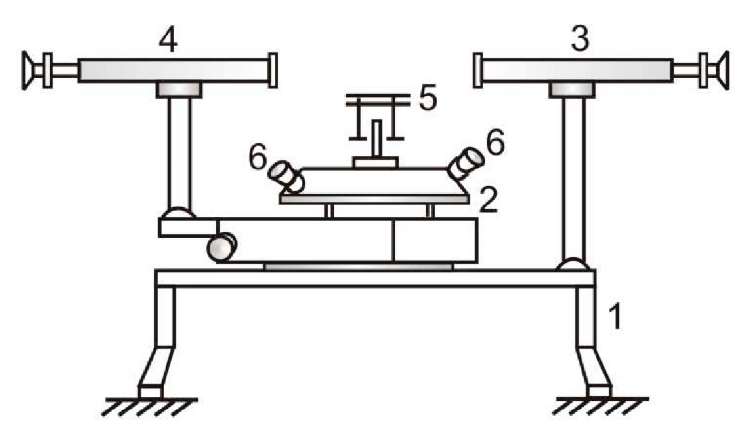 Рис. 6. Схема спектрометра-гониометра: 1 – штатив, 2 – угломерное устройство, 3 – зрительная труба, 4 – коллиматор, 5 – столик, снабженный установочными винтами, 6 – лупа для снятия отсчета угла. INCLUDEPICTURE "C:\\Documents and Settings\\Администратор\\Рабочий стол\\makogina\\media\\image8.jpeg" \* MERGEFORMATINET 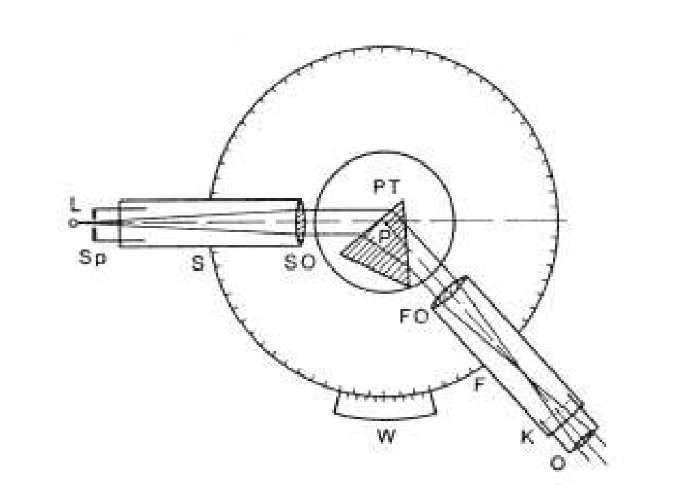 Рис. 7. Устройство и примерный ход лучей в спектрометре-гониометре:  - источник света,  - щель выдвижного тубуса,  - коллиматор,  - линза коллиматора,  - столик для призмы или дифракционной решетки с юстировочными винтами,  - призма,  - линза зрительной трубы,  - зрительная труба,  - окуляр,  - визирная нить,  - угломерное устройство с нониусом.В состав коллиматора 4 входит ахроматическая линза и щель регулируемой ширины , расположенная в фокальной плоскости линзы. Коллиматор служит для получения параллельных пучков лучей, падающих на решетку или призму. Наблюдение спектра производится с помощью зрительной трубы 3, настроенной на бесконечность.Угломерное устройство « представляет собой лимб, снабженный нониусом. Отсчет углов поворота зрительной трубы производится с помощью подвижной лупы 6, установленной над нониусом. В качестве диспергирующих элементов в работе используются две дифракционные решетки №1 и №2 и призмы из крона и флинта, которые устанавливаются на столик 5. Преломляющий угол обеих призм  , длина оснований -  .Перед выполнением работы необходимо заполнить таблицу 1. Таблица 1
5. Порядок выполнения работы. 1. Включите блок питания ртутной лампы. Ртутная лампа достигает максимальной яркости свечения после прогрева в течение 5 минут. При установке лампы проследите, чтобы воздух мог свободно циркулировать через вентиляционные отверстия в кожухе лампы. 2. Настройте спектрометр-гониометр. Для этого необходимо установить щель выдвижного тубуса объектива коллиматора против прорези защитного кожуха ртутной лампы. Регулируя расстояние между ними, надо добиться, чтобы изображение щели было четко видно в зрительную трубу. Это будет свидетельствовать о том, что щель находится в фокусе объектива коллиматора. 3. Установите на столике дифракционную решетку или призму. Внимание! При проведении эксперимента избегайте прямого попадания излучения ртутной лампы в глаза в течение длительного времени. Эксперимент 1. Определение длины волны спектральных линий ртути. 1. Длины волн, соответствующие всем видимым линиям спектра ртути, определяются с помощью дифракционной решетки, содержащей 600линий/мм 2. Поставьте решетку на столик гониометра так, чтобы изображение щели или максимум нулевого порядка совпал с ее изображением без решетки. Это означает, что на решетку падает нормально параллельный пучок лучей. Запишите показания угла гониометра в таблицу 2. 3. Вращая зрительную трубу относительно начального положения сначала влево, а затем вправо, найдите положение спектральных линий дифракционного максимума первого порядка. Выставляя в центр объектива зрительной трубы поочередно каждую спектральную линию, запишите в таблицу 2 значения углов и цвет соответствующих линий. Таблица 2.
4. Используя данные таблицы 2, по формуле (30) определите средние (из двух измерений) значения длин волн  , соответствующие всем видимым линиям спектра ртути. Определите абсолютную и относительную погрешность косвенного измерения длины волны . Сравните полученные результаты с табличными значениями длин волн для спектра ртути.5. Для всех найденных длин волн рассчитайте по формуле (29) ширину области дисперсии  в спектре первого порядка. Сравните полученное значение с абсолютной погрешностью измерения в данной работе. Сделайте выводы.6. По формуле (33) рассчитайте теоретическую разрешающую способность исследуемой решетки , необходимую для разрешения всех видимых линий спектра ртути во всех порядках дифракционного спектра.Примечание. Число щелей решетки можно рассчитать по формуле  где - период решетки,  - ширина пучка света, выходящего из коллиматора. |
