4.02 дисперсия электронов. 4.02 - Дисперсионная и разреш. способность призмы и дифракц. Дисперсионная и разрешающая способность призмы и дифракционного спектрометра Цель работы

• Название: Дисперсионная и разрешающая способность призмы и дифракционного спектрометра Цель работы
• Анкор: 4.02 дисперсия электронов
• Дата: 11.05.2021
• Размер: 0.75 Mb.
• Имя файла: 4.02 - Дисперсионная и разреш. способность призмы и дифракц. спе.doc
• Тип: Документы; #203568
• страница: 1 из 3

Дисперсионная и разрешающая способность призмы и дифракционного спектрометра

Цель работы: ознакомиться с классификацией, принципами действия и основными характеристиками дифракционных и призменных спектральных приборов и способами их определения.

Задачи:

1. измерить длину световых волн ртутной лампы с помощью дифракционной решетки;

2. определить дисперсию и разрешающую способность призменного и дифракционного спектроскопа.
1. Введение. Спектральные приборы и их характеристики.
В экспериментальной физике для разложения сложного излучения, поступающего в спектральный прибор, на монохроматические составляющие используют диспергирующие и интерференционные оптические элементы: призмы, системы призм и дифракционные решетки, соответственно. Физические явления, на которых основано применение призм и решеток, различны, но действие их на световые пучки во многом одинаково. Это позволяет для этих элементов измерять их свойства, раскладывать интенсивность излучения по длинам волн одними и теми же величинами – угловой дисперсией и разрешающей силой. Однако численные значения этих величин и зависимость их от длины волны у призм и решеток существенно различаются, и это определяет области применения их в спектральном исследовании. В этой связи выделяют два больших класса спектральных приборов, отличающихся по принципу регистрации спектров – это приборы дисперсионные и дифракционные.

Разделение излучений на монохроматические составляющие призмой является результатом зависимости угла отклонения прошедшего через призму луча от показателя преломления, который в свою очередь зависит от длины волны. Зависимость показателя преломления вещества от частоты (длины) волны света или зависимость фазовой скорости световых волн от их частоты называется дисперсией света. Действие призм основано на явлении дисперсии света. Распределение призмой интенсивности излучения по длинам волн называется дисперсионным спектром. Таким образом, в дисперсионном спектральном приборе устанавливается дисперсионный спектр, т.е. выделяются интенсивности (квадраты амплитуд) отдельных монохроматических составляющих, а информация об их фазах оказывается утраченной.

В интерференционном или дифракционном спектральном приборе (интерферометре) основной измеряемой характеристикой является фаза электромагнитного колебания, а не амплитуда световой волны и связанная с ней энергия. Напомним себе, что дифракция света (дифракционный спектр) есть многолучевая интерференция дифрагированного света, получаемая методом деления фронта волны от большого числа когерентных источников, которыми являются, например, щели решетки. Вследствие дифракции лучей на периодических структурах наблюдается дифракционный спектр.

Спектральные приборы можно также классифицировать по характеру решаемых с их помощью задач: спектроскоп – для визуального наблюдения, спектрограф – для фотографической регистрации спектра, спектрофотометр – для измерения распределения энергии по спектру, монохроматор – для выделения из спектра узкого интервала частот.

Интерферометры применяются в основном для решения задач, требующих от приборов предельно высокой точности. Регистрируется непосредственно сигнал на выходе, а затем осуществляется обработка сигнала методом преобразования Фурье, что позволяет представить зависимость интенсивности от частоты как комбинацию гармонических функций.

Принципиальная схема спектрального прибора приведена на рис.1 Освещаемая исследуемым излучением входная щель (Щ ) находится в фокальной плоскости объектива (линзы) коллиматора Л , который формирует параллельный пучок лучей и направляет его на диспергирующий элемент. Второй объектив Л - объектив зрительной трубы или телескопа, фокусирует вышедшие из диспергирующего элемента параллельные пучки. Наш глаз в выходной щели (Щ ) видит спектральные линии – это есть изображения входной щели, создаваемые параллельными пучками. Спектральные линии наблюдаются в разных местах фокальной плоскости линзы Л в зависимости от длины волны.

INCLUDEPICTURE "C:\\Documents and Settings\\Администратор\\Рабочий стол\\makogina\\media\\image1.jpeg" \* MERGEFORMATINET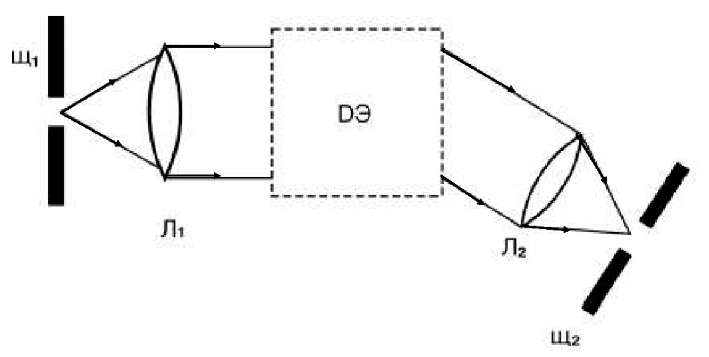

Рис. 1.Схема дисперсионного спектрального прибора: Щ - входная щель или апертура, Щ - выходная щель для глаза или фотопластинки, Л и Л - объективы коллиматора и зрительной трубы, соответственно, ДЭ – диспергирующий элемент.

Рассмотрим наиболее важные характеристики спектральных приборов.

Светосила спектрального прибора. Это энергетическая характеристика электромагнитного излучения в заданном спектральном интервале, попадающего в прибор и дающего вклад в формирование сигнала на выходе. Светосила определяется характером и размером входной апертуры (диафрагмы или щели), а также пропускающей способностью прибора.

Угловая дисперсия – величина, которая показывает изменение угла отклонения параллельного пучка света диспергирующим элементом при изменении длины волны на единицу. Она определяется отношением углового расстояния между двумя близкими спектральными линиями к разности соответствующих им длин волн:

, (1)

т.е. угловая дисперсия численно равна расстоянию между двумя спектральными линиями, длины которых отличаются на единицу. Угловая дисперсия выражается в радианах на ангстрем.

Линейная дисперсия – величина, численно равная расстоянию между двумя спектральными линиями, длины которых отличаются на единицу:

(2)

где - линейное расстояние между максимумами спектральных линий на экране.

Линейная дисперсия зависит не только от свойств диспергирующего элемента, но и от свойств объектива Л , используемого для наблюдения спектра. Чаще всего спектральные приборы характеризуют обратной линейной дисперсией:

. (3)

Разрешающая способность или разрешающая сила спектрального прибора определяет возможность его наблюдать раздельно две близлежащие спектральные линии с длинами волн и . Если две спектральные линии видны как раздельные, то говорят, что они разрешаются данным прибором. По определению:

, (4)

где - минимальная разница длин волн, разрешаемая спектральным прибором в данном спектре, если это дисперсионный спектр, или в данном порядке спектра, если спектр дифракционный.

Если линии имеют одинаковую интенсивность, то в соответствии с критерием Рэлея минимально разрешенными считают две монохроматические линии, для которых провал между максимумами составляет не менее 0,8 от интенсивности каждого из максимумов. Если угловое расстояние между максимумами , где - линейный размер диафрагмы, ограничивающий ширину пучка света и, соответственно, определяющий ширину спектральной линии, то с учетом угловой дисперсии разрешающая сила определится как

. (5)

Таким образом, теоретический предел разрешающей способности прибора равен произведению ширины параллельного пучка, выходящего из диспергирующего элемента, и угловой дисперсии.

Ширина области дисперсии (дисперсионная область) - предельная ширина спектрального интервала, при которой еще возможно получение неперекрывающихся максимумов. Пусть решетка освещается светом с длинами волн в интервале от до . В каком-то порядке максимум для длины волны наложится на максимум -го порядка длины волны , т.е. дифракционная картина становится неясной. Для дифракционной решетки:

. (6)
2. Элементарная теория дисперсии и призменный спектральный прибор.
Элементарная или классическая теория дисперсии описывает и объясняет дисперсию света на основе электронной теории Лоренца и электромагнитной теории света Максвелла. Основные положения электронной теории Лоренца формулируются следующим образом:

1) вещество представляет собой заряды и пустоту;

2) световые волны в среде распространяются с одной и той же скоростью;

3) заряженные частицы-электроны при взаимодействии со световой волной совершают вынужденные колебания около положений устойчивого равновесия, т.к. упруго связаны со всеми остальными зарядами, излучают электромагнитные волны и подчиняются законам классической электродинамики.

Таким образом, при выведении электрона из положения равновесия световой волной на него действует квазиупругая сила , природой которой является кулоновская сила. Совершая вынужденные колебания, электрон теряет свою энергию на излучение электромагнитных волн, а также теряет энергию при столкновениях, в результате чего возникает его радиационное и ударное торможение и, соответственно, происходит затухание колебаний. Затухание колебаний можно учесть, введя силу, аналогичную силе трения. Как и сила трения, она пропорциональна скорости колебаний . При прохождении через вещество плоской монохроматической световой волны в направлении распространения, например, вдоль оси z - - каждый электрон оказывается под действием электрической силы, изменяющейся по закону , где - амплитуда напряженности электрического поля световой волны, а ось совпадает с направлением распространения световой волны .

Пусть падающая световая волна будет плоскополяризованной, тогда все последующие формулы можно писать в скалярной форме. В этом случае уравнение движения упругосвязанного электрона в точке z=0 по второму закону Ньютона запишется как

. (7)

Уравнение (1) приведем к форме неоднородного дифференциального уравнения второго порядка

, (8)

где - квадрат собственной частоты колебаний электрона, - коэффициент затухания колебаний электрона. Для установившихся вынужденных колебаний уравнение (8) имеет решение в виде

, (9)

где - амплитуда вынужденных колебаний, которая зависит от частоты падающего света как

; (10)

Рассмотрим вынужденные колебания электрона согласно электромагнитной теории Максвелла, в которой электрон как частица принадлежит атому и упруго связан с его ядром. Смещение электрона от положения равновесия вызывает поляризацию атома (молекулы), дипольный момент которого изменяется со временем и равен , тогда с учетом формулы (10),он запишется как

(11)

Пусть явление дисперсии происходит в однородном изотропном неполярном, т.е. линейном диэлектрике, в котором можно пренебречь взаимодействием атомов или молекул. Поэтому математическое описание состояния диэлектрика можно проводить в скалярной форме. Согласно электромагнитной теории Максвелла, дипольный момент атома такого диэлектрика будет равен , где - поляризуемость атома (молекулы). Зависящая от частоты и изменяющаяся во времени поляризация всего диэлектрика определится вектором поляризации, равным , где - концентрация атомов, а с учетом формулы (11), вектор поляризации в скалярной форме запишется как

. (12)

Как видно из формулы (12) поляризуемость атома (молекулы) зависит от частоты падающего света

. (13)

Следуя теории Максвелла, электрическое смещение в диэлектрике определяется как , тогда, подставляя в данную формулу связь и , получим следующее выражение для линейного диэлектрика: или , где - диэлектрическая проницаемость диэлектрика (среды), она связана с показателем преломления для прозрачных сред по формуле .

Из выше приведенных рассуждений становится очевидной зависимость показателя преломления среды от частоты световой волны, падающей на нее,

. (14)

Как следует из формулы (14), показатель преломления среды является комплексной величиной, который имеет соответствующий вид: . Каков физический смысл комплексного показателя преломления, его действительной и мнимой части? Запишем уравнение световой волны, распространяющейся вдоль оси в среде с комплексным показателем преломления ,

, (15)

где . Подставляя это выражение в формулу (15), получим уравнение волны в виде:

, (16)

где - волновое число, в котором - действительный показатель преломления среды, - фаза волны, а - амплитуда распространяющейся в среде световой волны в зависимости от координаты . Из формулы (16) следует экспоненциальное уменьшение амплитуды световой волны. Следовательно, множитель экспоненты есть по смыслу коэффициент поглощения амплитуды волны, а - показатель поглощения, составляющий мнимую часть комплексного показателя преломления среды.

Пренебрегая взаимодействием молекул в модели однородного, изотропного линейного диэлектрика, пренебрегая множителем в формуле (14), получим результирующую формулу

, (17)

которая описывает зависимость квадрата показателя преломления от частоты падающей световой волны вдали от частот поглощения. Преобразуем формулу (17) следующим образом: при условии, что , а разложением в ряд по биному Ньютона, пренебрегая членами высших порядков. В результате преобразования получим формулу Коши или формулу нормальной дисперсии:

. (18)

Классическая теория излучения света атомами и молекулами является приближенной. Процесс излучения – это квантовый процесс. В квантовой теории процесс излучения описывается как процесс испускания фотонов возбужденными атомами при переходе их с более высоких энергетических уровней на более низкие энергетические уровни. Соответственно, в возбужденном состоянии не может одновременно находиться атомов (молекул). Пусть число излучающих атомов, переходящих с -го энергетического уровня на -й энергетический уровень, равно , тогда в области нормальной дисперсии ( ) зависимость показателя преломления от частоты падающей световой волны учетом дополнения (квантового приближения) запишется

. (19)

Формула (19) называется формулой Зельмейера. Формула Зельмейера позволяет теоретически рассчитывать показатели преломления для простых веществ в области частот световых волн, которые далеки от частот поглощения.

INCLUDEPICTURE "C:\\Documents and Settings\\Администратор\\Рабочий стол\\makogina\\media\\image5.jpeg" \* MERGEFORMATINET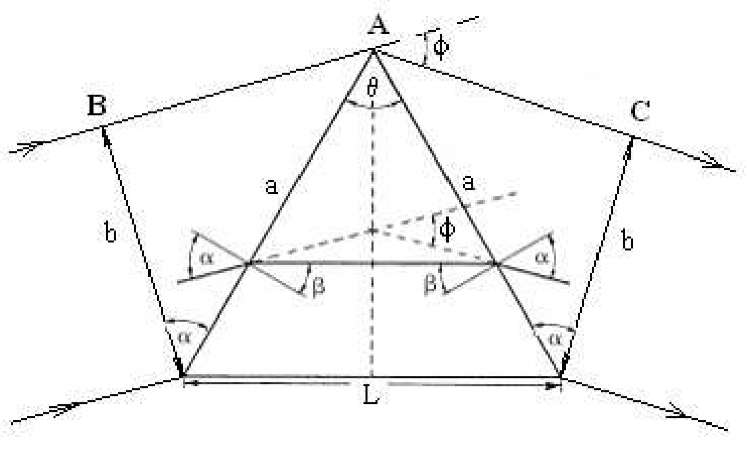

Рис. 2.Преломление световых лучей в призме при симметричной ее установке относительно коллиматора и зрительной трубы (угол - угол наименьшего отклонения).

В призменных приборах показатель преломления играет существенную роль в определении основных характеристик прибора. Наибольшая разрешающая сила призменного прибора достигается при симметричной установке призмы, когда угол отклонения вышедшего из призмы параллельного пучка света от падающего на призму параллельного пучка света минимален, как показано на рис.2.

По закону преломления

, (20)

где - показатель преломления оптического стекла призмы. Связь угла преломления и преломляющего угла призмы определяется как . Угол отклонения

, (21)

следовательно, 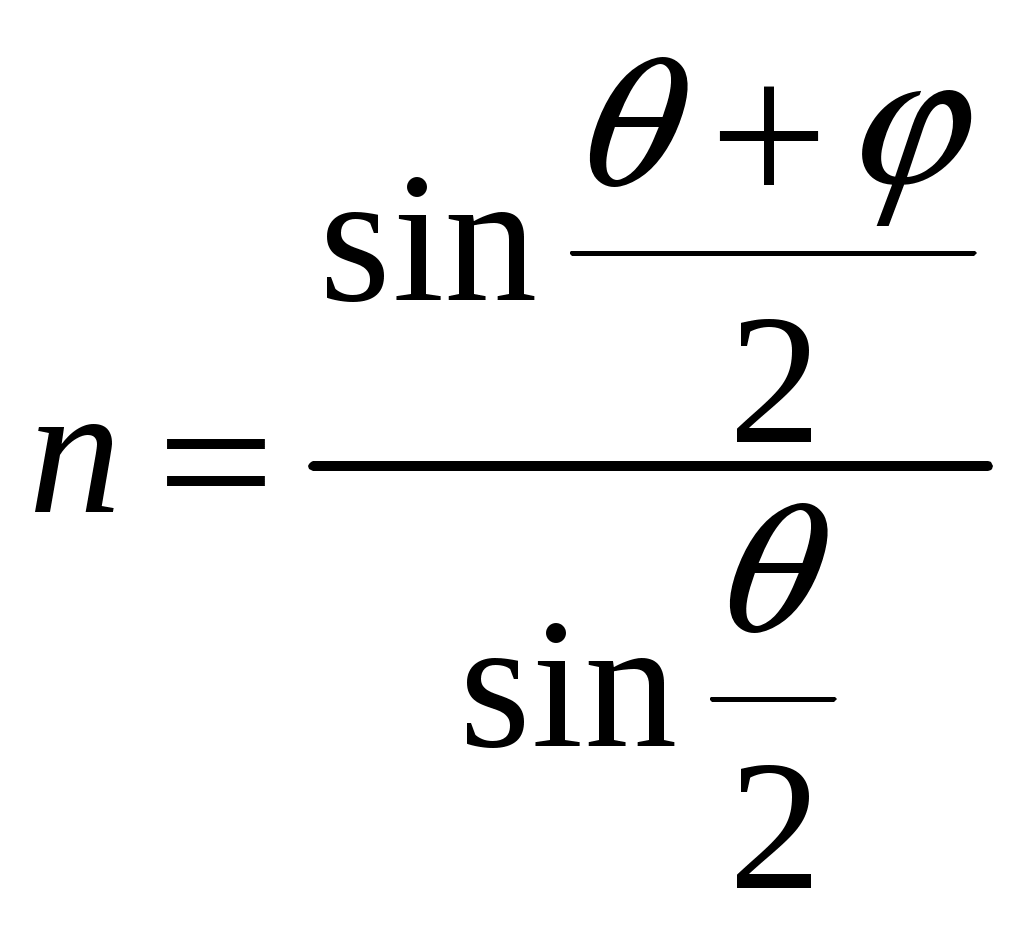, и

. (22)

Угловая дисперсия призмы обусловлена зависимостью ее показателя преломления от длины волны, и определяется согласно формуле (1) как

. (23)

Величина называется дисперсией вещества. Дифференцируя формулу (21) по величине , получаем

. (24)

Учитывая, что оптическая длина пути луча, идущего вдоль основания призмы, есть (рис.2), можно написать . Отсюда следует

. (25)

Поскольку , где - ширина пучка, ограниченного размерами призмы, то из формулы (25) следует, что и угловая дисперсия призмы равна

(26)

Первый сомножитель в формуле (23) можно найти также, дифференцируя формулу (22):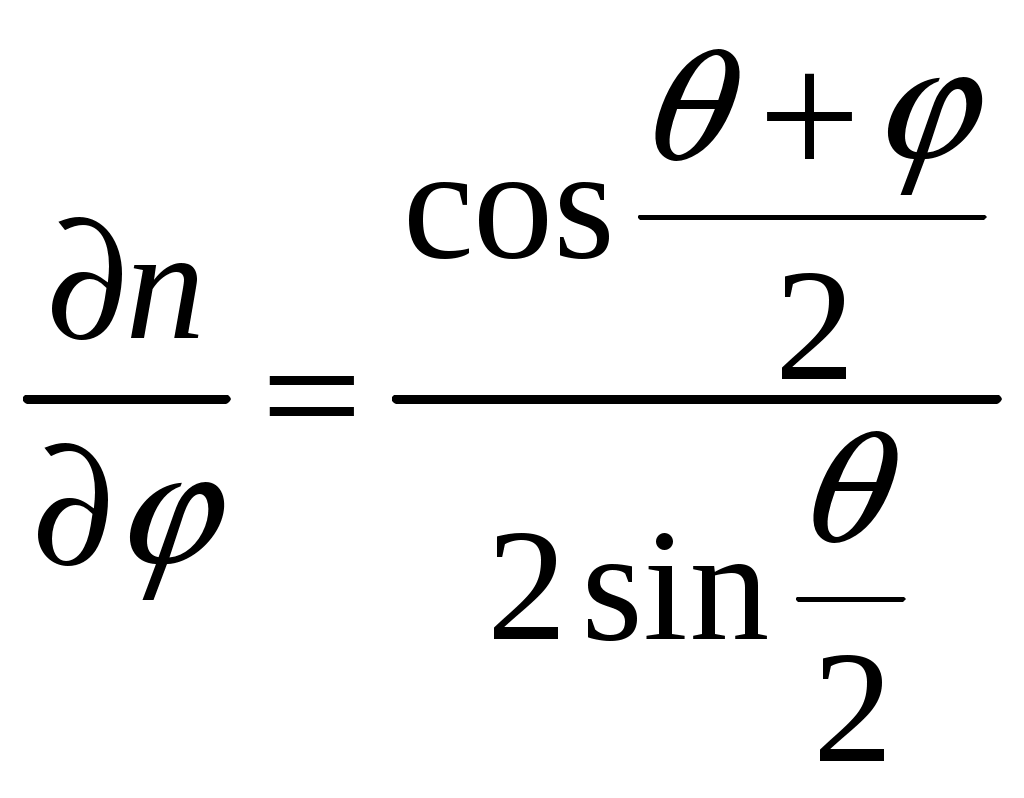

. (27)

Тогда угловую дисперсию призмы (23), с учетом формулы (22), можно выразить как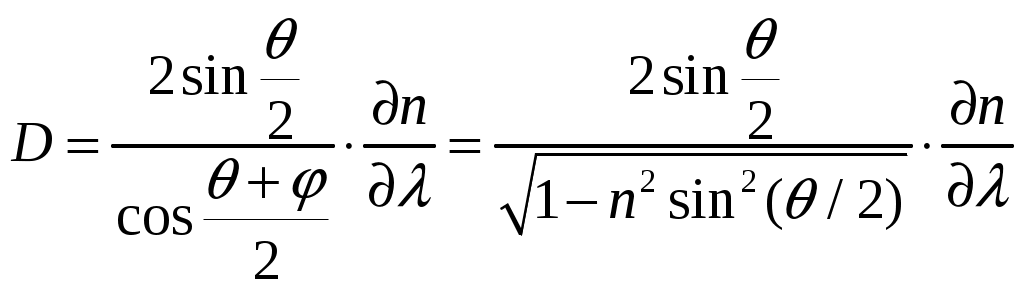

(28)

Как видно из формулы (28), чтобы достичь максимального спектрального разрешения призмы, необходимо использовать вещества с максимальными значениями показателей преломления и дисперсии .

Разрешающая способность призмы, в соответствии с формулой (4),

(29)

зависит от дисперсии вещества и длины основания призмы , но не зависит от преломляющего угла призмы . Однако с ростом угла уменьшается ширина пучка и растет дисперсия, что облегчает наблюдение спектра. Поэтому наиболее часто используют призмы с большим преломляющим углом . Один из существенных недостатков призмы состоит в быстром уменьшении характеристик и при продвижении в длинноволновую часть спектра.