Диссертация на соискание ученой степени кандидата технических наук Владимирский государственный университет

• Название: Диссертация на соискание ученой степени кандидата технических наук Владимирский государственный университет
• Анкор: zashchita-informatsii-v-telekommunikatsiyakh-asu-tp-khimicheskoi-promyshlennosti
• Дата: 12.04.2023
• Размер: 6.36 Mb.
• Имя файла: zashchita-informatsii-v-telekommunikatsiyakh-asu-tp-khimicheskoi.doc
• Тип: Диссертация; #1055613
• страница: 18 из 25

^аУ> ⁼ / ^а1т Ь --П

Поскольку матрица (4.4.7) может быть интерпретирована как матрица парных сравнений рангов, то для экспертных оценок элементов этой матрицы можно использовать 9-бальную шкалу Саати: щ = г; / Эта шкала приведена ранее, в Таблице 4.4.

Таким образом, с помощью полученных формул (4.4.6), экспертные зна­чения о рангах элементов или их парные сравнения преобразуются в функцию принадлежности нечеткого терма [93].

Алгоритм построения функции принадлежности включает в себя сле­дующие операции:

1. 
   Задать лингвистическую переменную;
   

А =

Определить универсальное множество, на котором задается лингвис­тическая переменная

;

2. 
   
   
3. 
   Задать совокупность нечетких термов {8_Ь 8₂, ... , 8_т}, которые исполь­зуются для оценки переменной;
   
4. 
   Для каждого терма 8^ ]=1..ш сформировать матрицу (4.4.7);
   
5. 
   Используя формулы (4.4.6) вычислить элементы функций принадлеж­ности для каждого терма.
   

Нормирование найденных функций осуществляется путем деления на наибольшие степени принадлежности.

Функции принадлежности применяются при выборе рационального вари­анта СЗИ (п. 4.5.3), а также при определении важности требований к СЗИ в случае, когда экспертные оценки заданы в качественной форме.

4.5 Выбор рационального варианта СЗИ на основе экспертных оценок

4.5.1 Анализ методов выбора рационального варианта СЗИ

Принципиальными особенностями решения задачи выбора рационально­го варианта СЗИ, определяющими метод ее решения являются [112-114]:

• 
  многокритериальное^ задачи выбора;
  
• 
  не только количественное, но и качественное (нечеткое) описание показате­лей качества СЗИ, задаваемых в виде требований;
  
• 
  при нечеткой постановке задачи влияние на выбор метода ее решения экс­пертной информации, определяющей предпочтение того или иного показа­теля [91-93].
  

Рассмотрим указанные особенности решения задачи более подробно. Общая постановка задачи многокритериальной оптимизации [97]: Пусть X — |х_ь...,х_;,...,х_п| - вектор оптимизируемых параметров некоторой системы 8. Некоторое ]-е свойство системы 8 характеризуется величиной ]-го показателя ^(Х); ] = 1„т. Тогда система в целом характеризуется вектором по­казателей О = Задача многокритериальной оптимизации сводит­ся к тому, чтобы из множества М₅ вариантов системы 8 выбрать такой вариант (систему 8о), который обладает наилучшим значением вектора р. При этом

предполагается, что понятие «наилучший вектор предварительно сформу- лированно математически, т.е. выбран (обоснован) соответствующий критерий предпочтения (отношение предпочтения).

Анализ литературы [106, 107] показывает, что все многочисленные мето­ды решения многокритериальных задач можно свести к трем группам методов:

• 
  метод главного показателя качества;
  
• 
  метод результирующего показателя качества (аддитивного, мультиплика­тивного, максиминного);
  
• 
  лексикографический метод (метод последовательных уступок).
  

Принципиальной особенностью рассматриваемой задачи выбора рацио­нального варианта СЗИ АСУ ТП является преимущественно качественный ха­рактер показателей, трактуемых как требования к СЗИ. В связи с этим рассмат­риваемые методы многокритериальной оптимизации должны формулироваться в нечеткой постановке.

Как в классической, так и в нечеткой постановке выбор метода решения многокритериальной задачи определяется тем, в каком виде представлена экс­пертная информация о предпочтении показателей или их важности. Для этого приведем таблицу, которая позволяет обоснованно выбирать метод нечеткой многокритериальной оптимизации в зависимости от экспертной информации о предпочтении показателей (Таблица 4.7).

Таблица 4.7 Выбор метода решения в зависимости от экспертной информации Экспертная информация о степени пред­почтения или важности показателей	Метод решения многокритериальной задачи
отсутствует	максиминный метод
показатели упорядочены по важности	лексикографический метод
определены весовые коэффициенты показателей	аддитивный показатель мультипликативный показатель максиминный показатель

4.5.2 Выбор варианта СЗИ по аддитивному показателю

Поскольку, в нашем случае весовые коэффициенты показателей качества СЗИ определены — используем метод аддитивного показателя для выбора оп­тимального варианта СЗИ «ПХВ-1».

Метод результирующего показателя качества основан на формировании обобщенного показателя путем интуитивных оценок влияния частных показа­телей качества ..., на результирующее качество выполнения системой ее функций. Оценки такого влияния даются группой специалистов - экспертов, имеющих опыт разработки подобных систем.

Наибольшее применение среди результирующих показателей качества получили аддитивный, мультипликативный и минимаксный показатели.

Аддитивный показатель качества представляет собой сумму взвешенных нормированных частных показателей и имеет вид:

т

^ , (4.5.1)

где ^с*³ — нормированное значение ]-го показателя;

С^ - весовой коэффициент ]-го показателя, имеющий тем большую вели­чину, чем больше он влияет на качество системы. =1; > 0; ] = 1..ш.

Для 5 вариантов СЗИ «ПХВ-1» в результате экспертного опроса получе­ны данные о степени выполнения каждого из 4 показателей качества.

Варианты оцениваются по 4 требованиям (критериям), описанным выше (п. 4.3.1): С1 - требования к аппаратным СЗИ, С₂ — требования к программным СЗИ, Сз - требования к структуре, С4 — требования к нормативной базе. С, = { 0,9/аь 0,9/а₂; 0,8/а₃; 0,6/а₄; 0,7/а₅ } С₂ = { 0,8/аь 0,9/а₂; 0,7/а₃; 0,8/а₄; 0,9/а₅ } С₃ = { 0,5/аь 0,7/а₂; 0,8/а₃; 0,9/а₄; 0,8/а₅ } С₄ = { 0,6/а,; 0,7/а₂; 0,6/а₃; 0,7/а₄; 0,4/а₅ }

Расчет аддитивного показателя качества СЗИ «ПХВ-1» по формуле (4.5.1) приведен в Таблице 4.8

.

Таблица 4.8 - Расчет аддитивного показателя качества СЗИ «ПХВ-1»	СЗИ,	сзи2	СЗИз	сзи4	сзи5	Отн. Вес. показате­ля качест­ва
С,	0,9	0,9	0,8	0,6	0,7	0,614
с2	0,8	0,9	0,7	0.8	0,9	0,239
Сз	0,5	0,7	0,8	0,9	0,8	0,103
с4	0,6	0,7	0,6	0,7	0,4	0,044
Аддитив­	0,8217	0,8706	0,7673	0,6831	0,7449
ный показа­
тель

Сравнение вариантов СЗИ по аддитивному показателям» уровня качества представлено на графике (Рисунок 4.5).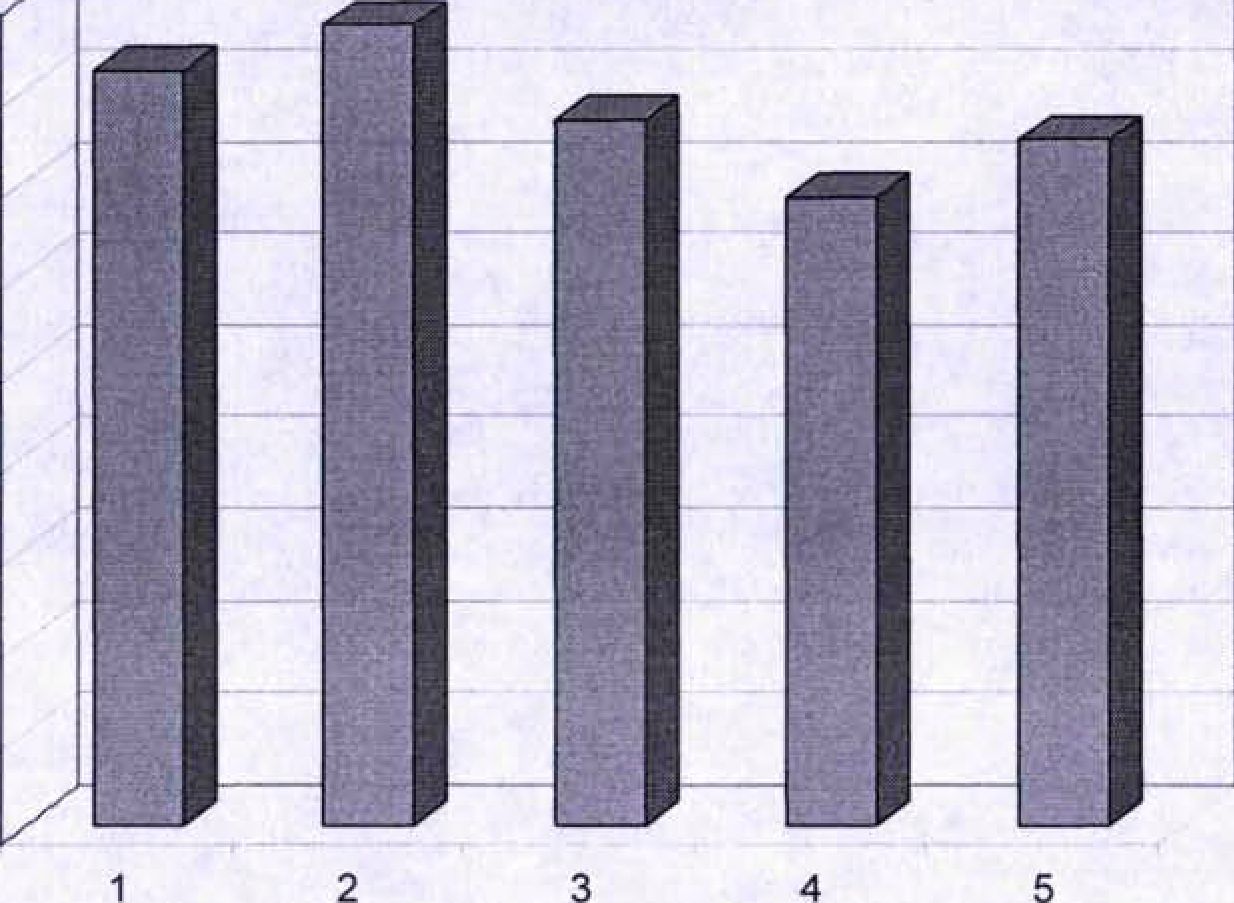




Рисунок 4.5 - Сравнение вариантов СЗИ по аддитивному показателяю уровня качества

0,9 0,8 0,7 0.6 0,5 0,4 0,3 0,2 0,1 0

Таким образом, наилучшим является второй вариант СЗИ. По графику (Рисунок 4.5) легко определить, насколько тот или иной вариант защиты соот­ветствует обобщенным требованиям

.
4.5.3 Выбор варианта СЗИ при задании требований в качественной форме

Если оценки вариантов по критериям и коэффициенты относительной

важности задаются функциями принадлежности соответственно _и

Vw^j)

Необходимо упорядочить m вариантов СЗИ а_ь а₂, ..., а_т, оцениваемых по «п» требованиям (критериям) Сь Сг, ..., С_п. Соответствующую оценку обозна­чим Ry; i=l..m, j=l..n. Относительная важность каждого требования задается коэффициентом Wj , £Wj =1. В этом случае взвешенная оценка i-ro варианта

вычисляется по формуле: и

/=1 (4.5.2)

Так как в данном случае Ry и Wj являются нечеткими числами, Rj опреде­ляется в соответствии с формулой (4.5.2) на основе принципа обобщения. Би­нарную операцию * (в данном случае это операция сложения или умножения) можно обобщить на случай нечетких чисел (например, X и Y), задаваемых функциями принадлежности ц._х(х) и ц.у(у) соответственно. Результат обобщен­ной операции * - нечеткое число Z, определяемое функцией принадлежности:

fi_z(z) = sup min(//_v(.x),/i_K

г-**У (4.5.3)

После того, как взвешенные оценки R; получены, необходимо сравнить варианты на их основе. Для этого вводится нечеткое множество I, заданное на множестве индексов вариантов {1, 2, ..., ш}. Значение соответствующей функ­ции принадлежности интерпретируется как характеристика степени того, на­сколько вариант а.\ является лучшим. Значение ji ¡(1) вычисляется по формуле:

¡л_т{/)= sup millДд (ry)

> (4.5.4)

4.5.4 Выбор варианта СЗИ лексикографическим методом

В случае, если весовые коэффициенты показателей не определены, но упорядочены по важности — возможно использование лексикографического метода выбора [105]. Данный метод, в отличие от метода аддитивного показа­теля, позволяет только определить какой из вариантов СЗИ лучше, но не возво- ляет определить на сколько.

Суть метода заключается в выделении сначала множества альтернатив с наилучшей оценкой по наиболее важному показателю. Если такая альтернатива единственная, то она считается наилучшей; если их несколько, то из их под­множества выделяются те, которые имеют лучшую оценку по второму показа­телю и т.д.

Для расширения множества рассматриваемых альтернатив и улучшения качества решения по совокупности показателей может назначаться уступка, в пределах которой альтернативы считаются эквивалентными.

Применение этого метода при нечетких показателях качества (требовани­ях) СЗИ сводится к следующим операциям [113].

1. 
   Упорядочить требования к СЗИ по важности: Ci > С₂ > ... > Cj > ... > C_n; j = l..n.
   
2. 
   С согласия ЛПР для каждого требования назначается величина допус­тимой уступки ACj; j = l..n. в пределах которой рассматриваемые варианты СЗИ считаются «практически равноценными».
   
3. 
   Для первого требования С] формируется множество «практически рав­ноценных» вариантов, удовлетворяющих условию - множество щ.
   

t*i

4. 
   Если тс 1 - множество содержит ровно один вариант, то он и считается наилучшим. Если щ - множество содержит более одной альтернативы, то пе­реходим к рассмотрению всех вариантов множества tïi по требованию С₂.
   
5. 
   Для второго требования С₂ формируется 7Ь

множество вариантов из множества к ь удовлетворяющих условию:

max .Л'с, (а^) - /fc (a_k) < tC-,

Л-IT,

6. 
   Если 712 множество содержит ровно один вариант, то он и считается наилучшим; если более одного - рассматриваем эти варианты по требованию С₃ и т.д.
   
7. 
   Если все требования последовательно пересмотрены и в результате по­лучаем 7Г — множество % = щ • • ... ■ 7С„, содержащее более одной альтернати­вы, то возможно применить два подхода:
   

• 
  уменьшить величину допустимой уступки A Cj, начиная с первого по важности требования и повторить все шаги решения;
  
• 
  представить ЛПР окончательный выбор лучшего варианта.
  

Выбираем наиболее подходящий из 5 вариантов СЗИ «ПХВ-1» (aj) лекси­кографическим методом.

Варианты оцениваются по 4 требованиям (критериям), описанным выше (п. 4.3.1): Ci - требования к аппаратным СЗИ, С₂ - требования к программным СЗИ, С₃ - требования к структуре, С₄ - требования к нормативной базе.

В результате экспертной оценки получены следующие данные, характе­ризующие степень соответствия СЗИ заданным требованиям:

С, = { 0,9/аь 0,9/а₂; 0,8/а₃; 0,6/а₄; 0,7/а₅ }

С₂= { 0,8/а,; 0,9/а₂; 0,7/а₃; 0,8/а₄; 0,9/а₅ }

С₃ = { 0,5/аь 0,7/а₂; 0,8/а₃; 0,9/а₄; 0,8/а₅ }

С₄ = { 0,6/а,; 0,7/а₂; 0,6/а₃; 0,7/а₄; 0,4/а₅ }

1. 
   Требования упорядочены по важности следующим образом: С, >С₂>С₃ >С₄
   
2. 
   Зададимся величиной допустимой уступки:
   

A Cj = 0,1 для всех Р_{; угр}.

3. 
   Формируем множество по первому требованию. При максимальном значении Ci = 0,9 и A Ci = 0,1 в это множество входят варианты Л\ = {аь а₂, а₃}.
   
4. 
   Из элементов множества л\ формируем множество %₂ по второму тре­бованию. При шах С₂=0,9