Диссертация на соискание ученой степени кандидата технических наук Владимирский государственный университет
 Скачать 6.36 Mb. Скачать 6.36 Mb.
|
|
и к п т ¥ = 'А(]1' °ч/'х0 + X ХЛ'" °Ч/ • } /=и=1 /=1у=А+1 (4.2.14) Таким образом, задача создания СЗИ АСУ ТП в виде (4.2.1), (4.2.2) сводится к оптимальному обоснованию количественных и качественных требований к СЗИ, при допустимых затратах, и принимает вид: Найти: шах ил (х^; 1=1..п; ]=1..т) (4.2.15) при ограничении: С(х^) < Сд0П\ ¡=1 ..п; ]=1 ..т. В соответствии с формулировкой задачи (4.2.15) основными этапами ее решения являются: сбор и обработка экспертной информации о характеристиках угроз: частоте появления 1-й угрозы и ущербе Дqj (¡=1 ..п); сбор и обработка экспертной информации для определения важности выполнения ]-го требования для устранения ьй угрозы ау и функции принадлежности р.(ху), (1=1..п; ]=1..т); оценка стоимости СЗИ для конкретного варианта ее реализации, зависящая от степени выполнения требований С (х^; 1=1..п; ]=1..т); выбор рационального варианта СЗИ АСУ ТП (рационального задания требований) в соответствии с постановкой (4.2.15) как задачи нечеткого математического программирования. Отметим, что при отсутствии информации об угрозах для решения задачи (4.2.15) может быть использован показатель вида: " к » "I '•=и=1 ¡=и=к+\ (4.2.16)
Предотвращенный ущерб от 1-й угрозы до и после применения рекомендаций по защите показан на Рисунке 4.2. 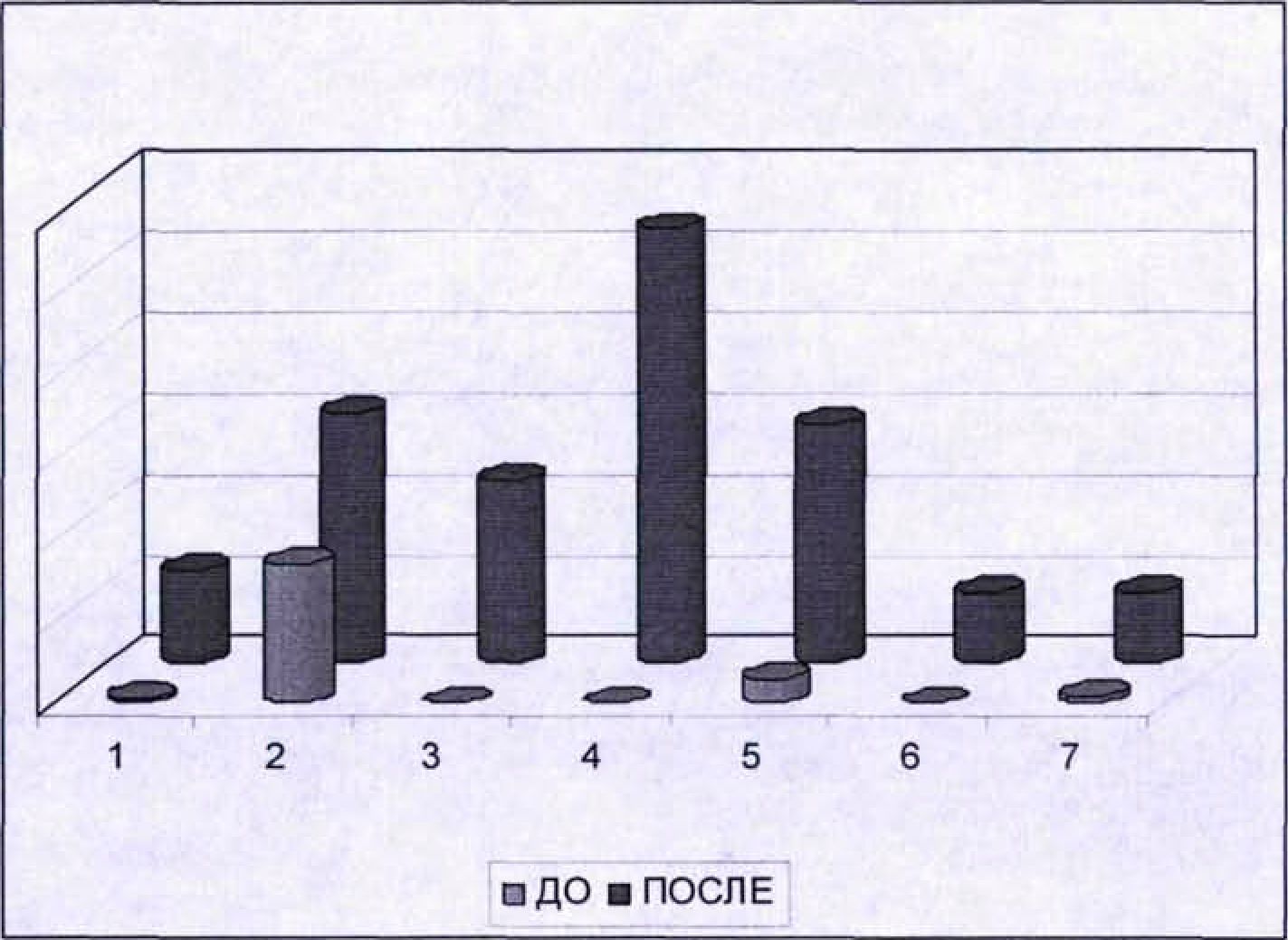 Рисунок 4.2 - Предотвращенный ущерб от 1-й угрозы Относительная опасность (относительный ущерб) и относительная частота появления (вероятность появления) ¡-й угрозы представлены на Рисунке 4.3. 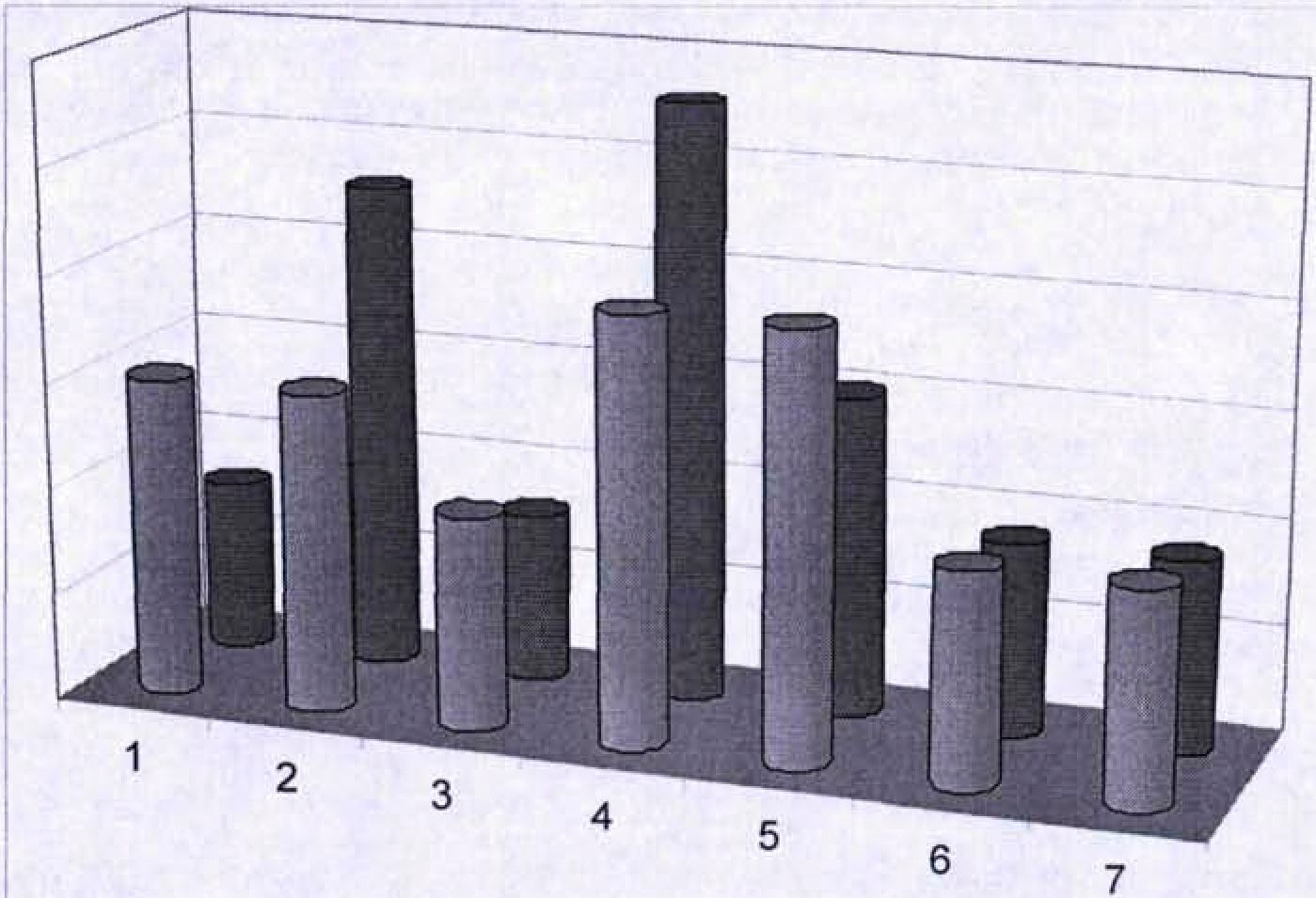 I Относительная опасность угрозы ■ Относительная частота появления Рисунок 4.3 - Относительная опасность и относительная частота появления ¡-й угрозы 4.3 Определение важности требований, предъявляемых к СЗИ При выборе наилучшего варианта системы защиты информации в соответствии с полученым нами критерием, возникает задача определения важности (веса) требований, предъявляемых к параметрам СЗИ. Наиболее полный обзор методов определения коэффициентов важности приведен в литературе [98]. Иерархическая классификация методов определения коэффициентов важности требований приведена на Рисунке 4.4. Методы определения коэффициентов важности критериев
1А.2.2Л 1А.2.2.2 Рисунок 4.4 - Иерархическая классификация методов определения коэффициентов важности критериев При решении практических задач обоснования требований и оценки систем защиты информации возникает вопрос рационального выбора метода определения весовых коэффициентов из числа 19 групп изложенных в [98-102] методов. Неправильный выбор метода приводит к недостаточной обоснованности производимых операций над малодостоверными исходными экспертными данными . Автором решается задача выработки рекомендаций для проектировщиков АСУ ТП малой и средней сложности. Проектировщики таких АСУ ТП как правило представляют из себя малые предприятия, с числом сотрудников от 5 до 10. Решения принимает директор предприятия, реже — ведущий специалист. Поэтому главным критерием выбора метода оценки следует принимать простоту получения экспертных данных при высокой степени согласованности мнений экспертов и при минимальном количестве экспертов. Поэтому автором проведен анализ методов определения весовых коэффициентов с целью выбора наиболее подходящих для решения задачи определения важности требований, предъявляемых к СЗИ АСУ ТП. Анализ литературы [98, 106 и др.] позволяет определить основные факторы, влияющие на выбор метода оценки весовых коэффициентов. Рассмотрим эти факторы. Физическая сущность параметров и отношение между ними. Параметры (в нашем случае требования к СЗИ) определяются исходя из смысла провозглашенной цели. Далее необходимо определить степень взаимосвязей между ними, т.е. зависимости или независимости. Характер зависимости или независимости (независимость по полезности, по предпочтению, по безразличию и т.д.) влияет на выбор метода оценки. Сложность проведения экспертизы и трудоемкость получения экспертной информации. Сложность и трудоемкость экспертизы определяется реальными условиями и возможностями ее проведения. Как показано в [98], наименьшего времени общения с экспертами требует ранжирование и метод Терстоуна; метод линейной свертки требует наибольшего времени общения с экспертами (в 12 раз больше, чем ранжирование; в 2 раза больше, чем метод Черчмена-Акофа) и т.д. Степень согласованности мнений экспертов. Степень согласованности в зависит от количества привлекаемых экспертов и уровня их квалификации. В то же время на нее влияет выбранный метод оценки весов. Так, наибольшую согласованность экспертов обеспечивает линейная свертка, наименьшую - непосредственная численная оценка весов, при этом ранжирование при его простоте позволяет получить весовые коэффициенты достаточно точные и близкие к их значению, полученному методом линейной свертки. 4. Трудоемкость обработки экспертных данных. Этот фактор не является главным при современном уровне развития вычислительной техники. Однако, применение сложных методов обработки экспертной информации может потребовать разработки специальной программы обработки, что повлияет на сроки проведения экспертизы. Очевидно, что наиболее простыми методами с этой точки зрения являются ранговые методы и балльные методы. Учет приведенных факторов позволяет на практике выбрать рациональный вариант оценки весовых коэффициентов применительно к СЗИ АСУ ТП. Метод Саати, по мнению автора, является оптимальным по совокупности факторов для поставленной задачи. 4.3.1 Определение важности требований, предъявляемых к СЗИ, методом Саати Суть метода: Результаты попарного сравнения параметров описываются отношениями их весов, т.е. представимы в виде матрицы А (матрицы Саати). А = || / Ау ||; уе1..п. А=я2/я, 1 ... ык (43Л) 4,/я, К'К - 1 Справедливо следующее равенство [101], (А - пЕ)'А = 0 (4.3.2) где Е - единичная матрица; А - вектор весов . Для нахождения вектора весов Л необходимо решить уравнение (4.3.2). Поскольку ранг матрицы равен 1, то п — единственное собственное число этой матрицы и, следовательно, уравнение (4.3.2) имеет ненулевое решение. Более того, это единственное решение, обладающее свойством: = 1- Это решение и есть искомый вектор относительных весов параметров — вектор Саати. А = 1 5 1/5 1 1/6 1/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
