Дрістер тезистері

• Название: Дрістер тезистері
• Дата: 29.03.2022
• Размер: 2.07 Mb.
• Имя файла: 4_тезисы лекции.doc
• Тип: Документы; #424352
• страница: 2 из 7

Әдебиеттер: 2, бет. 51-57; 5, бет. 11-18; 7, бет.45-62.
Бақылау сұрақтар:

1. Жұмыс ұғымына анықтама бер.

2. Жұмыс қандай параметрлерге тәуелді?

3. Жұмыстың негізгі қасиеттерін ата.

4. Қайтымды процесстің қайтымсыз процесстен айырмашылығы?

5. Жылу сыйымдылығы дегеніміз не?

6. Жылу сыйымдылығының негізгі түрлерін ата.

7. Термодинамиканың бірінші заңына сәйкес жылу нее тең?
Тақырып 3: Идеал газдарадың термодинамикалық процестері.

Мақсаты: газдардың идеалды процестерін үйрену, әр процестегі параметрлер күйін анықтау.
Жоспар:
1. Процестерді зерттеудің жалпы сұрақтары

2. Изохоралық процесс

3. Изобаралық процесс

4. Изотермиялық процесс

5. Адиабаталық процесс

6. Политропты процесс
1 Процесстерді зерттеудің жалпы сұрақтары.

Термединамиканың бірінші заңы жылу мөлшері, газдың сыртқы жұмысы және ішкі энергия өзгерісі арасында байланыс орнатады. Жіберілген немесе алынған жылу процеске байланысты.

Теориялық зерттеулерде, сонымен қатар техникадағы тәжірибелік жұмыстарда қолданылатын негізгі процесстер мыналар: изохоралық - тұрақты көлемде жүретін процесс,изобаралық – тұрақты қысымда жүретін процесс, изотермиялық – тұрақты температурада жүретін процесс, адиабаталық – сыртқы ортамен жылу алмасу жүрмеген кездегі процесс.

Сонымен қатар, белгілі бір шарттарда негізгі процесстер үшін ортақ процесстер – политропты процесстер бар.

Зерттеудің жалпы әдестері барлық процесстерге бекітілген, олар мыналарға негізделген:

1. P-V- және T-Sдиаграммаларында процесстің қисық теңдеуі шығарылады;

2. Процесстің басында және соңында жұмыс денесінің негізгі параметрлері арасында байланыс орнатады;

3. Меншікті газдың барлық процесстеріне арналған формула бойынша ішкі энергия өзгерісін анықтау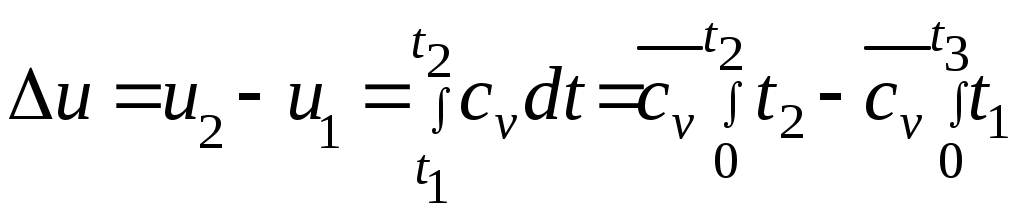



немесе тұрақты жылу сыйымдылығы кезінде:



Жұмыс және газ көлемінің өзгерісі негізгі формула бойынша анықталады: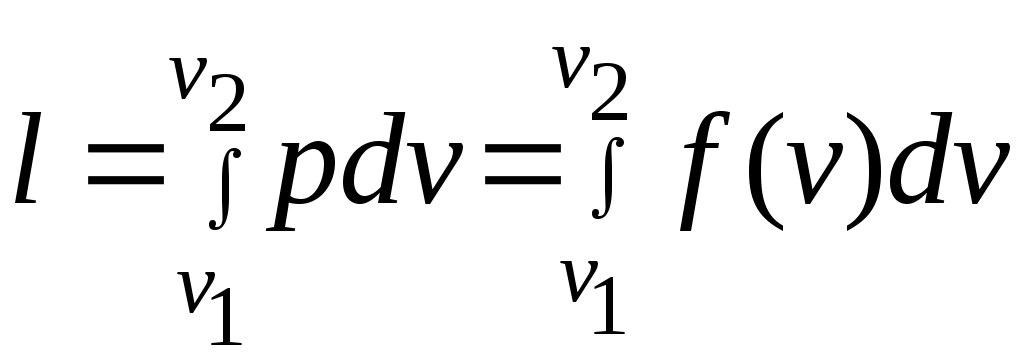



Меншікті жылу мөлшері мына формуламен анықталады: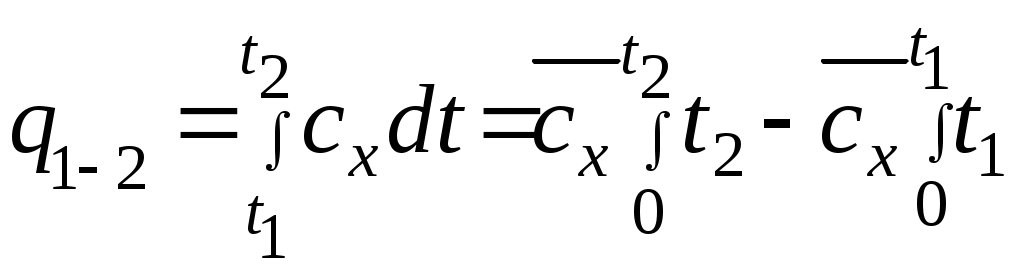



Идеал газдардың барлық процесстеріне арналған формула бойынша меншікті энтольпия өзгерісі мына формуламен анықталады: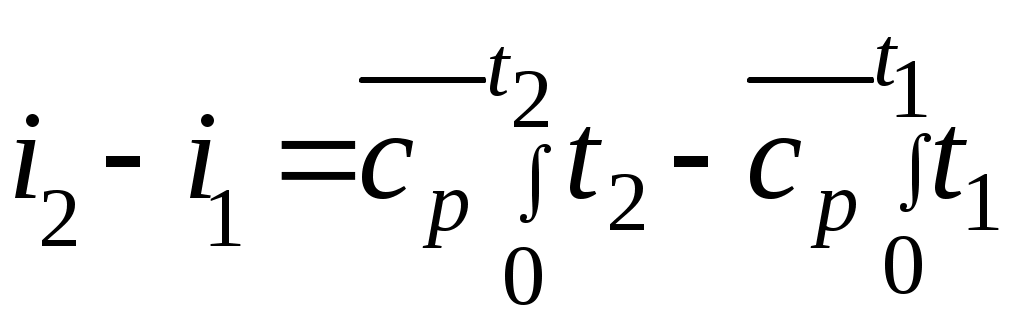



немесе тұрақты жылу сыйымдылығы үшін:



Идеал газдардың меншікті энтольпия өзгерісі мына формуламен анықталады:





Қарастырылған процесстер қайтымды болып табылады.

2 Изохоралық процесс.

Тұрақты көлемде жүретін процесс изахоралық деп аталады (dv = 0, немесе v = const). 3.1 суретте изахоралық процесстің графигі берілген.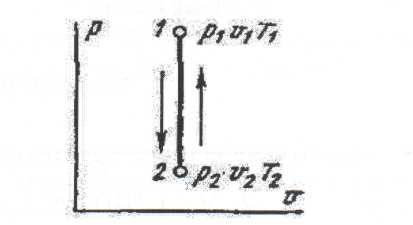


Сурет 3.1 - P-V диаграммадағы изахоралық процесс бейнеленген.

Идеал газдың күй теңдеуінен , кезінде мынаны аламыз



Тұрақты көлем кезінде газ қысымы абсолютті температураға тура пропорционалды өзгереді: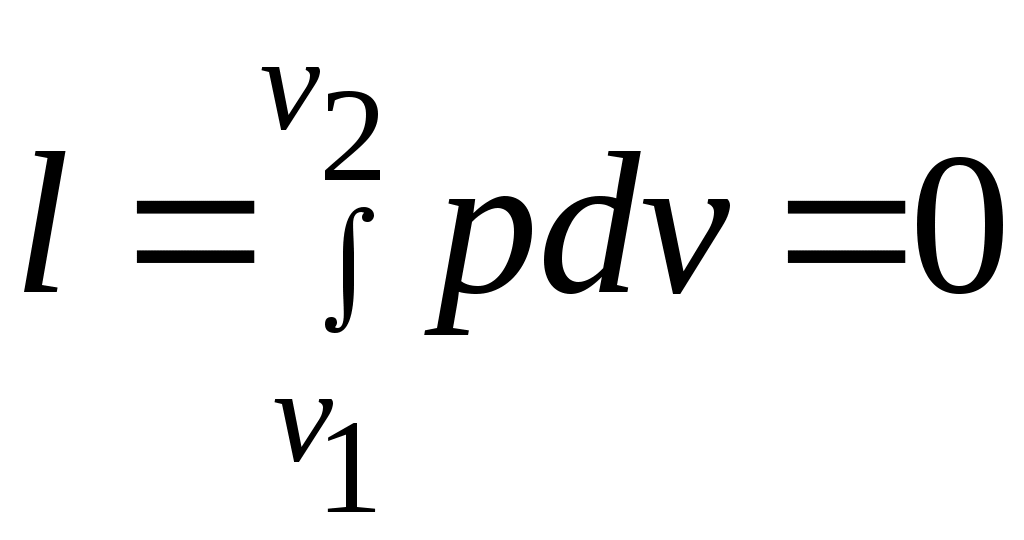
(3.1)
кезінде газдың сыртқы жұмысы нөлге тең, өйткені, . Осыдан,



Меншікті сыртқы жұмыс 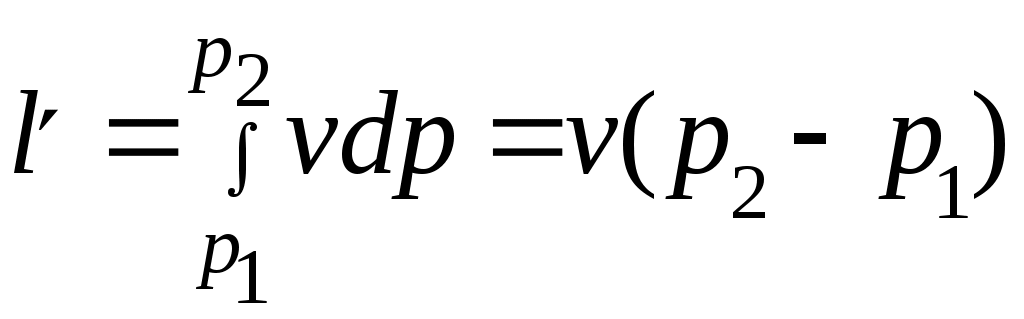мына формуламен анықталады:




Термодинамиканың бірінші заңының негізгі формуласы (2.12) кезінде мынадай түрге келеді



Жылу сыйымдылығы тұрақты кезінде жылу мөлшері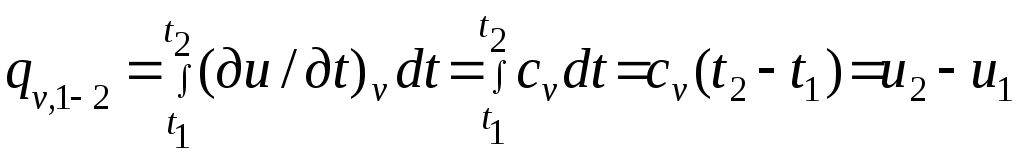



Жылу сыйымдылығы ауыспалы кезінде 1-2 процессте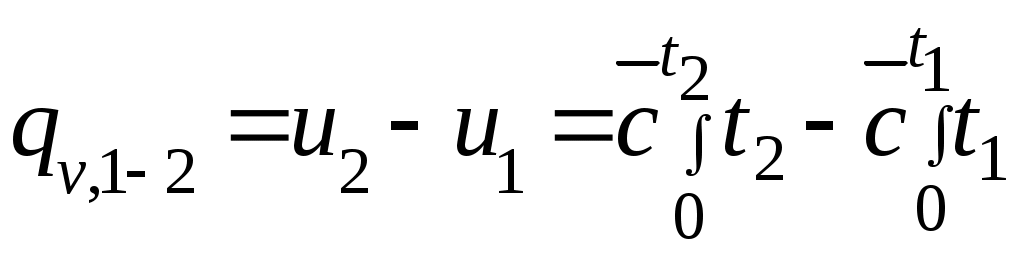

(3.2)

Қайтымды изохоралық процессте меншікті энтольпия өзгерісі мына теңдіктен анықталады: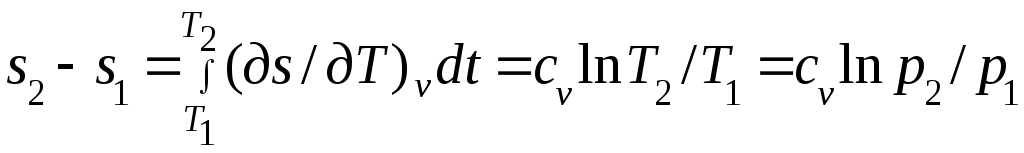



кезінде , сондықтан жылу сыйымдылығы тұрақты болған жағдайда меншікті энтропия өзгерісі мынаған тең:

(3.3)

- диаграммасындағы изохора 1-2 қисығы болып табылады (сурет. 3.1). 1-2 қисығына жанама сызық оның әр нүктесінде нақты жылу сыйымдылығын береді .

2 – нүктедегі жанама аналитикалық изометрия ережесі бойынша мынаған тең:



Әр түрлі көлемді изохоралар, бір температурада бұрыштық коэффициенті бірдей, эквидистантты қисықтар болып табылады.

Әр түрлі көлемдер үшін құрылған изохоралар кезінде мына формуламен анықталады (сурет 3.2):



3 Изобаралық процесс.

Тұрақты қысым кезінде жүретін процесс изобаралық деп аталады (dp = 0, немесе р = const). Процесс қисығы изобара деп аталады. 2 суретте процесс графигі бейнеленген.

Идеал газ күйінің теңдеуінен изобаралық процесс үшін



Бұл қатынас Гей-Люссак заңы деп аталады. 2 процесс үшін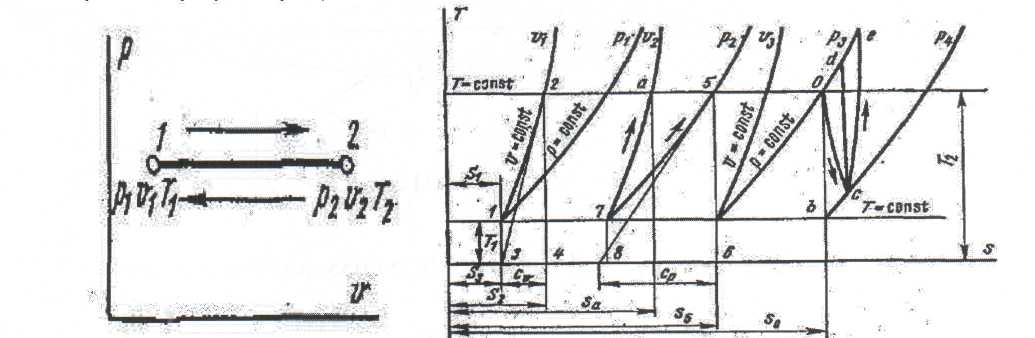
(3.4)


Сурет 3.2 - P-V және T-S диаграммаларындағы изобаралық процесс.

Бір мөлшерлі газдардаң көлемі изобаралық процессте абсолютті температураға тура пропорционалды өзгереді.

Газ кеңейген кезде оның температурасы өседі, ал сығылған кезде төмендейді.

Осыдан көлемнің өзгерген меншікті жұмысы мына теңдеумен өрнектеледі: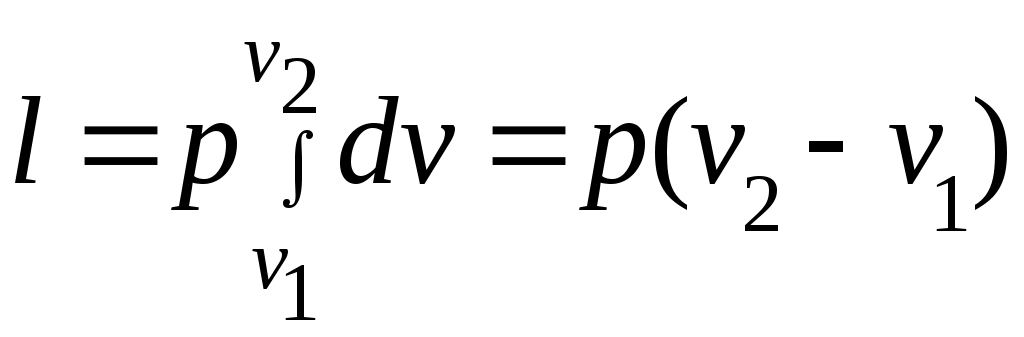

(3.5)

немесе

(3.6)

Меншікті сыртқы жұмыс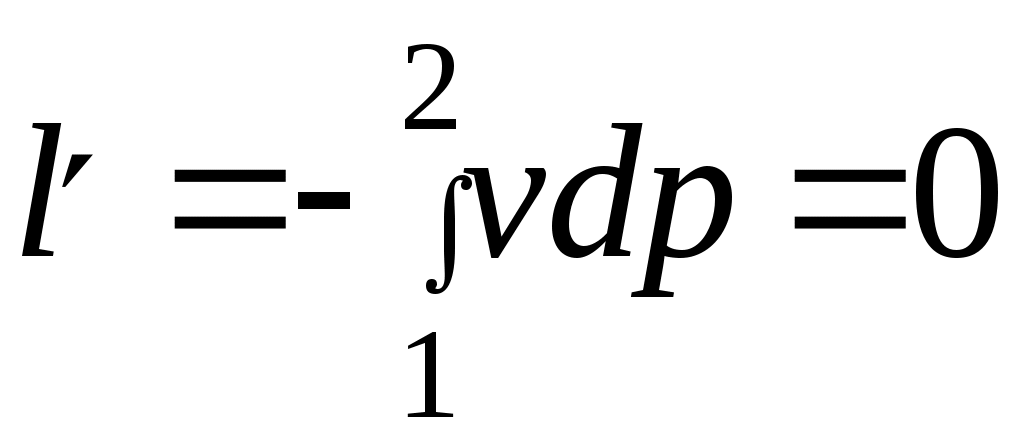



Меншікті ішкі энергияның өзгерісі



кезіндегі термодинамиканың бірінші заңының теңдеуі мына түрде болады



Осыдан, тұрақты жылу сыйымдылығы кезіндегі изобаралық процессте денеге хабар беретін меншікті жылу мөлшері мынаған тең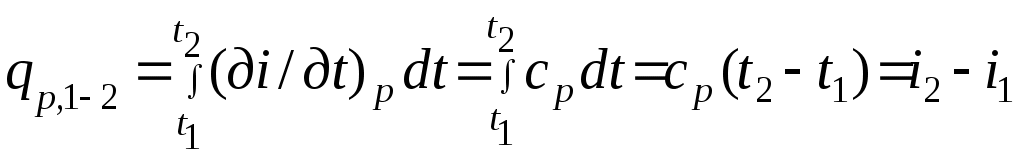

(3.7)

ауыспалы жылу сыйымдылығы кезінде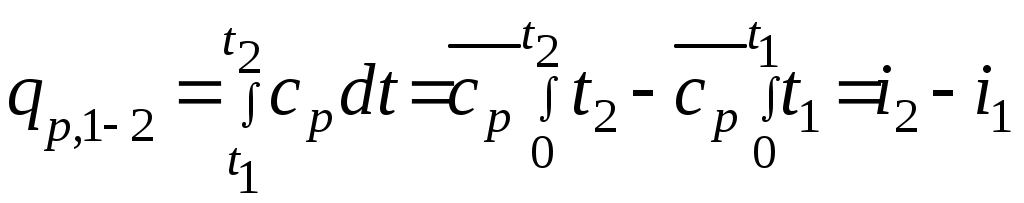

(3.8)

тең меншікті жылу мөлшерінің хабарланған бөлігі кеңею жұмысына айналады, ал екінші бөлігі дененің меншікті ішкі энергиясының ұлғаюына әкеледі.

Тұрақты жылу сыйымдылығы кезіндегі қайтымды изобаралық процесс үшін меншікті энтропия өзгерісі мына теңдеуден анықталады:



бірақ 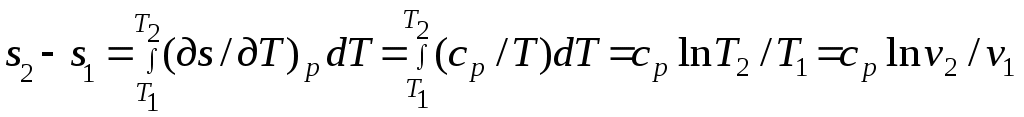кезінде

(3.9)

Ts- диаграммасындағы изобара 7-5 қисығымен бейнеленген (сурет 3.2). 7-5 қисығының жанамасы оның әр нүктесінде нақты жылу сыйымдылығының мәнін . береді. 5 – нүкте үшін жанама



Бір температурада бұрыштық коэффициенті бірдей барлық изобаралар эквидистантты қисықтар болып табылады. кезінді әр түрлі көлемді изобаралар арасындағы көлденең арақашықтықтар мына теңдеуден анықталады (3.9), (сурет 3.2):



Изобаралар арасындағы арақашықтық қысымға және газ табиғатына байланысты екенін соңғы теңдеуден көруге болады.Газ қысымы неғұрлым үлкен болса, изобара соғұрлым координат өсіне жақынырақ орналасады.

4 Изотермиялық процесс

Тұрақты температура кезінде жүретін процессті изотермиялық деп атайды 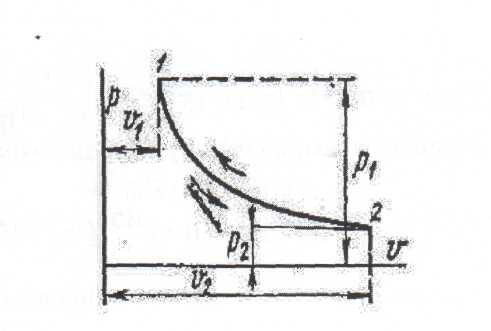немесе (сурет. 3.3).


Сурет 3.3 - P-V және T-S диаграммаларындағыизотермиялық процесс

Идеал газдардың изотермиялық процессі үшін



немесе

и (3.10)

Тұрақты температура кезінде газ көлемі оның қысымына пропорционалды өзгереді ( Бойль-Мариотта заңы ).

P-V диаграммасында изотермиялық процесс теңбүйірлі гиперболоид түрінде беріледі.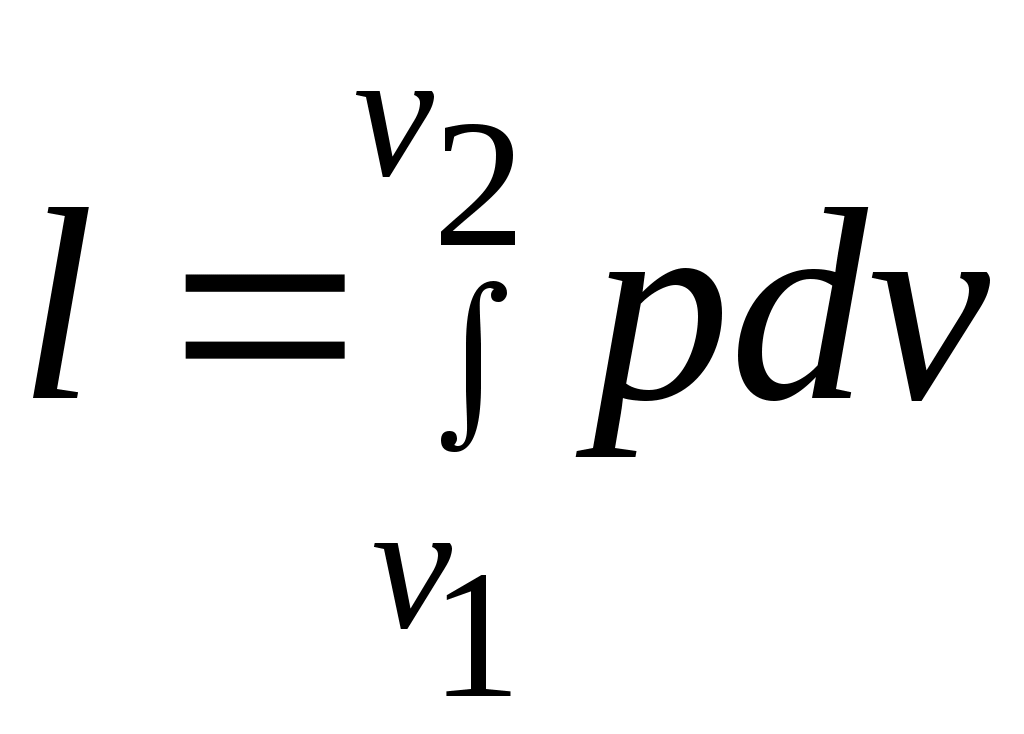

кезіндегі термодинамиканың бірінші заңының негізгі теңдеуі қарапайым түрге келеді:

,

изотермиялық теңдеуден 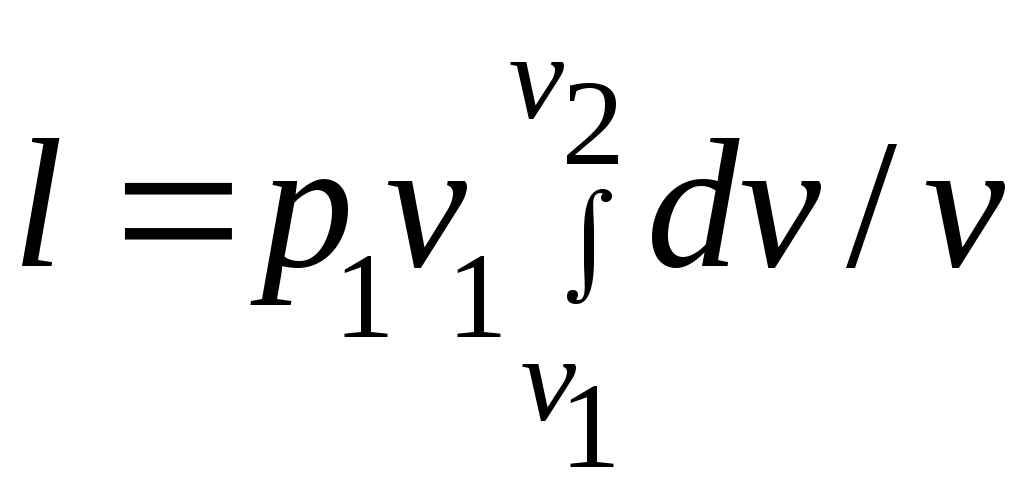немесе сондықтан



Соңғы теңдеуді интегралдау арқылы мынаны аламыз

(3.11)
(3.11) теңдеуінен идеал газдың меншікті жұмысын және сыртқы меншікті жылу мөлшерін анықтайды. Ондық логарифмге ауыссақ, ондаам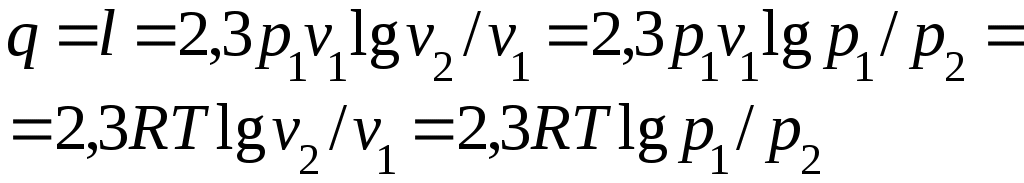

(3.12)

Меншікті жұмыс 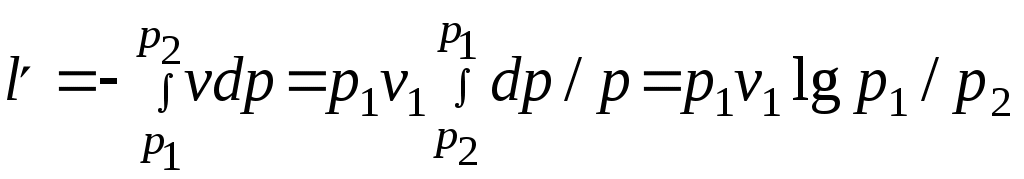мына формула бойынша анықталады

(3.13)

яғни идеал газдың изотермиялық процессінде . Изотермиялық процессте жылу сыйымдылығы мына формуламен анықталады:



Идеал газдың энтальпиясы және ішкі энергиясы өзгермейді, яғни және .

- диаграммасында изотермиялық процесс абсцисса өсіне параллель түзумен бейнеленеді (сурет 3.2). Меншікті энтропия өзгерісі:



и (3.14)

Изотермиялық процесстегі меншікті жылу мөлшері Т абсолютті температурада меншікті энтропия өзгерісіне тең :



5 Адиабаталық процесс

Жылу берусіз жүретін процесс, яғни жұмыс денесінің қоршаған ортамен жылу алмасусыз жүретін процесс адиабаталық деп аталады.Адиабаталық процессті алу үшін қажетті шарт: , осыдан .

Термодинамиканың бірінші теңдеуінен болса, онда

және

Бірінші теңдеуді екіншісіне бөлсек, онда 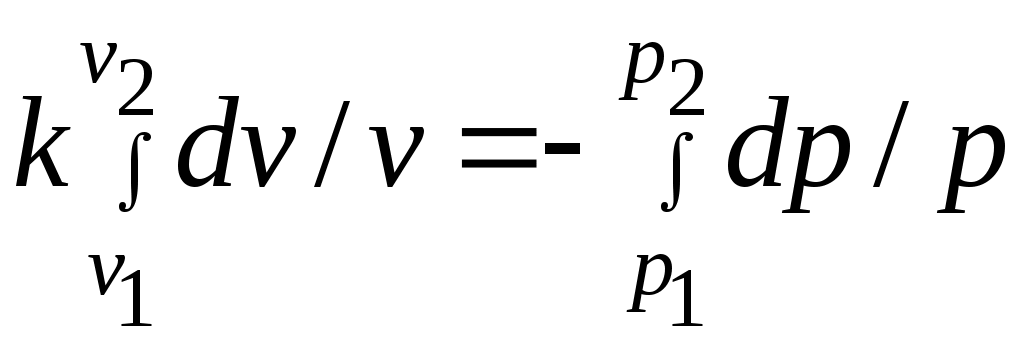немесе .

және ескере отырып соңғы теңдеуді интегралдау арқылы мынаны аламыз

және

немесе
осыдан адиабата теңдеуі

(3.15)

Адиабаталық процесстегі газ қысымы мен көлемінің дәрежесі тұрақты шама. шамасын адиабата көрсеткіші деп атайды. Адиабаталық процессте негізгі параметрлер арасындағы тәуелділікті қарастырайық.

Адиабата теңдеуінен

және

Егер бұл парамертлер қатынасын процесстің күй теңдеуіне 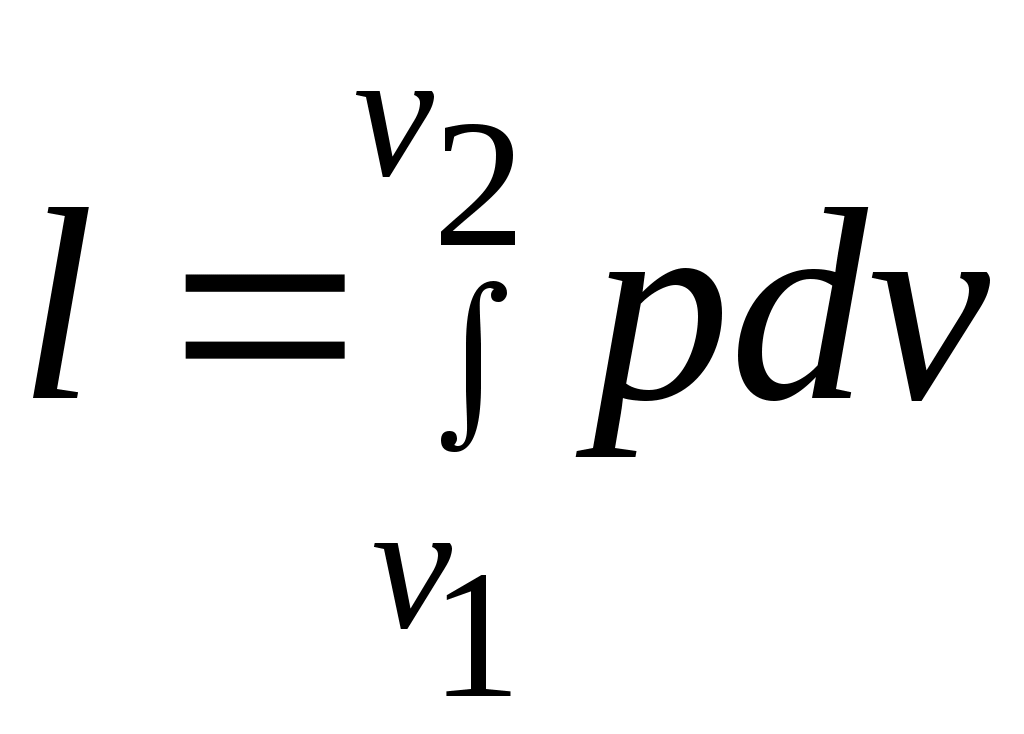қоятын болсақ, онда түрлендірілуден кейін



меншікті жұмыс көлемінің өзгерісі адиабаталық процессте,

немесе





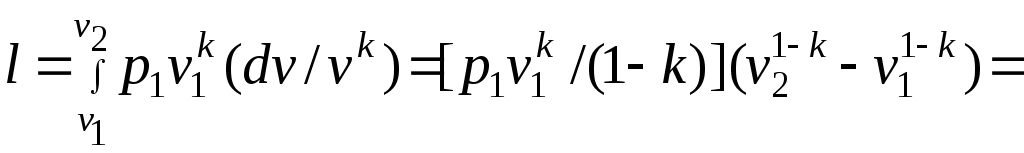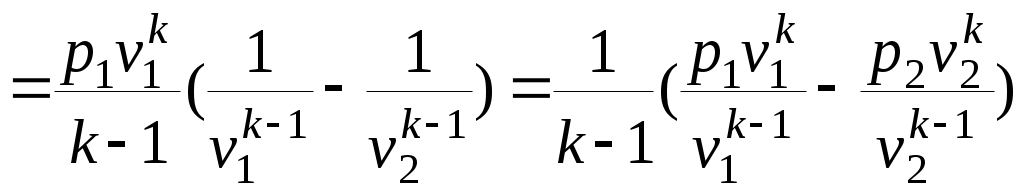Осыдан

(3.16)

(3.16) өрнегінен келесі формулаларды алуға болады:



Температуралар қатынасын клем мен қысымның қатынасымен ауыстырамыз: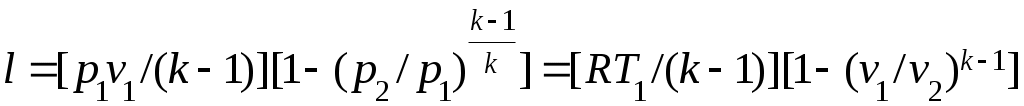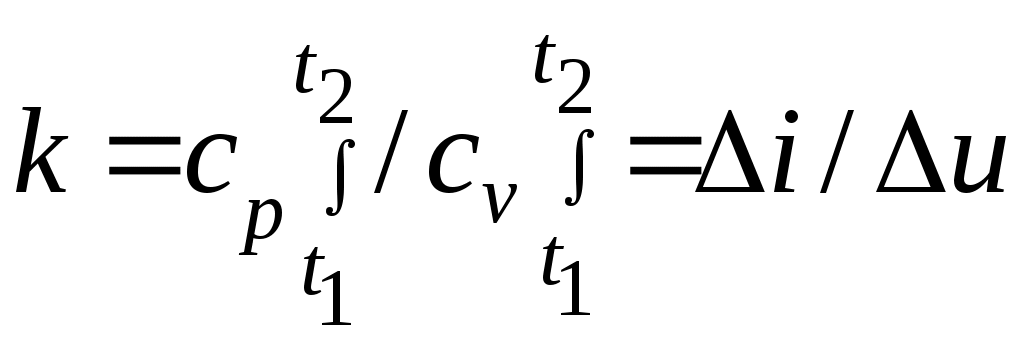



арасындағы тәуелділіктер және жұмыс теңдеуі шартында алынды. Ауыспалы жағдайда орташа мәнін алады:

.

(2.11) және (2.12) термодинамиканың бірінші заңының теңдеуі адиабаталық процесс үшін мына түрде болады:

и ,

Осыдан

и

Бұл қатынастан мынаны алуға болады .

Алынған теңдеу адиабаталық (изоэнтроптық) процесстің дифференциалды теңдеуі.

Бұл теңдеуде .

Термодинамиканың бірінші заңына сәйкес меншікті жылу көлемінің өзгерісі 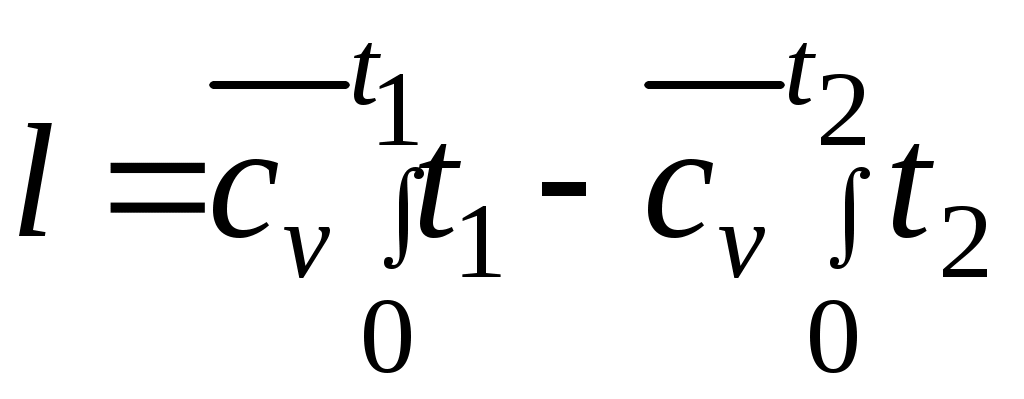кезінде



кезінде

.

Егер газ кеңейсе, онда ішкі энергия және температура азаяды, ал егер газ сығылса, онда ішкі энергия және температура ұлғаяды.

кезінде өрнегінен адиабаталық процессте меншікті жылу нөлге тең.

Адиабаталық процесстегі сыртқы жұмысты табайық: .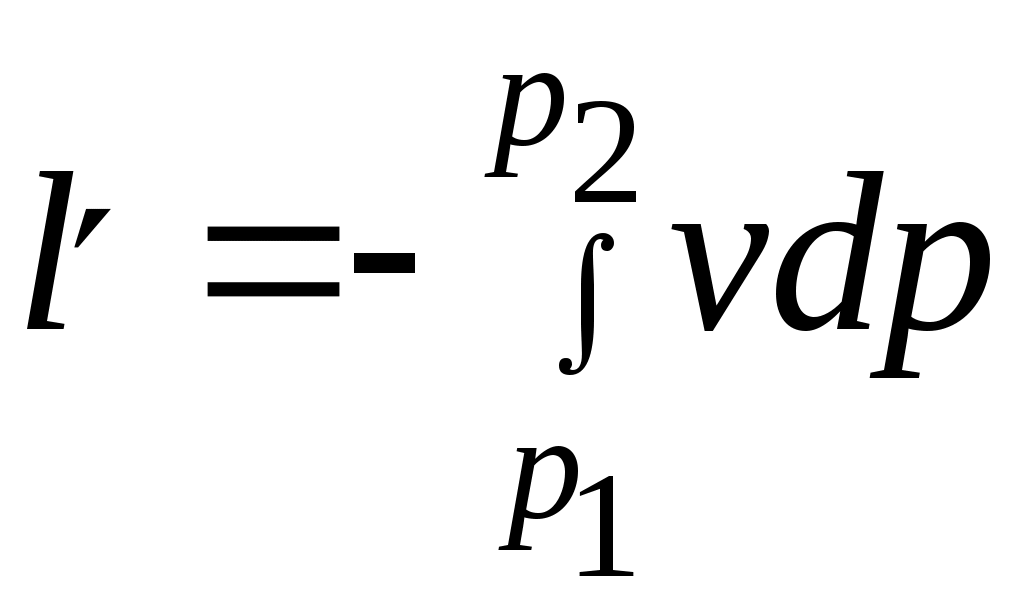

Адиабата теңдеуінен (3.15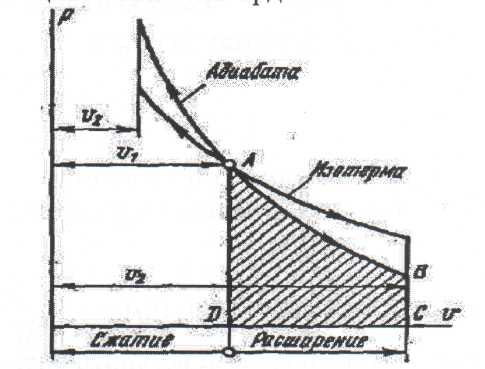) немесе , яғни .

Осыдан,

(3.17)

және .

диаграммасында сыртқы жұмыс ABCD (сурет 3.4) ауданымен беріледі. Ол шеткі абцисса және ординат өсімен, процесс сызығымен шектеледі.



Сурет 3.4 - Адиабата және изотерманың P-V диаграммасы

Қайтымды процесс үшін , сондықтан және , (3.18) яғни қайтымды адиабаталық процесс изоэнтропты (немесе тұраты энтропия кезінде) болып табылады.

Қайтымсыдз адиабаталық процессті Ts — диаграммада көрсетуге болады. Қайтымсыз процесстерге термодинамиканың бірінші заңын (2.11) қолдана отырып, және Sq_mp> және Т > 0 ескере отырып, қайтымсыз адиабаталық процесстің изоэнтропты емес екенін көруге болады (меншікті энтропия өзгерісі бірге тең емес).

6 Политропты процесс

Жылу сыйымдылығы тұрақты кезінде жүретін процесс политропты деп аталады.

Политропты процесстің меншікті жылу сыйымдылығы дейінгі оң және теріс қабылдауы мүмкін.

Политропты процесстегі меншікті жылу мөлшері бастапқы және ақырғы температураларының және процесстің жылу сыйымдылығының с_п көбейтіндісімен өрнектелуі мүмкін:

және (3.19)
Политропты процесстің теңдеуі термодинамиканың бірінші заңының теңдеуінен шығады:

және

Бұл теңдеуден табамыз. Теңдеудің сол жағын деп белгілеп, мынаны аламыз және .

Алынған теңдеуді процесстің бастапқы және ақырғы шегінде интегралдаймыз

немесе

(3.20)

Алынған теңдеу политропты процесс теңдеуі деп аталады. политроп көрсеткішінің әр процесс үшін белгілі бір сандық мәні бар. Негізгі процесстер үшін: изохоралық , изобаралық , изотермиялық және адиабаталық .



Политропты процесстің меншікті жылу сыйымдылығы мына формуладан анықтаймыз:



(3.21)

Егер (3.21) теңдеуге әр процесс үшін мәнін қойсақ, онда:

Изохоралық процесс ,

Изобаралық процесс ,

Изотермиялық процесс ,

Адиабаталық процесс , .

Политропты процесстегі меншікті жұмыстың теңдеуі:
(3.22)

немесе



(3.23)
Полтропты процессте газдың меншікті ішкі энергия өзгерісі және меншікті жылу мөлшері мына формуламен анықталады:



(3.24)

Политропты процесстің сыртқы жұмысы аналогиялық жағынан адиабаталық процесске тең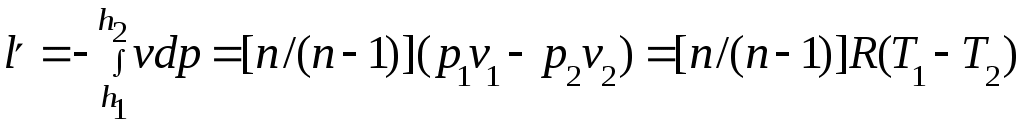

(3.25)

Меншікті энтальпия өзгерісі

(3.26)

Кез келген политропты процессте 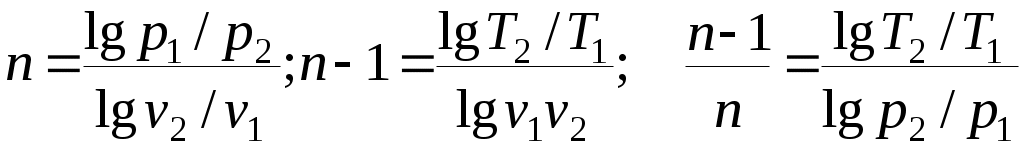мәні графиктің екі нүктесінің координаталары бойынша анықтауға болады:
(3.27)

Полтропты процессті логарифмдік координатта көрсеткішін табу үшін мына әдісті қолдануға болады: .

Бұл теңдеу и координаттарында түзу сызықты береді, ал политроп көрсеткіші - тангенс бұрышы абсцисса өсіне тік (3.27).

Политропты процессте газдың меншікті энтропия өзгерісі мына формуламен анықталады: ,

немесе күйдің соңғы өзгерісі: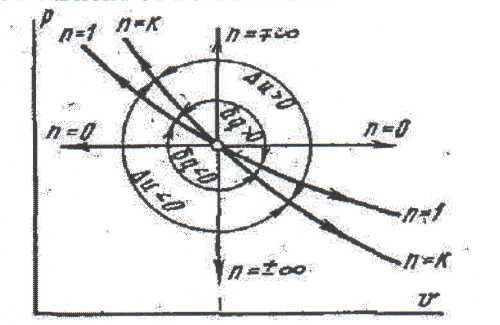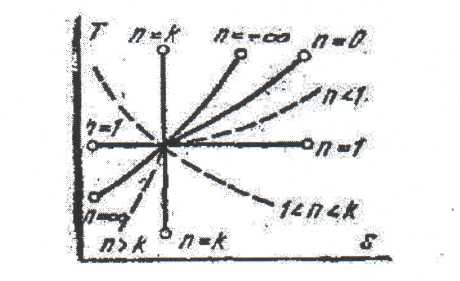

(3.28)





Сурет 3.5 - P-V және T-S политроп диаграммасы

3.5 суретте көрсеткішке тәуелді нүктеден шығатын -диаграммасындағы политропты процессі берілген.

Политропты процессте газдық меншікті ішкі энергиясы қалай өзгеретінін қарастырайық. Изотермиялық процессте n=1 тең болған жағдайда газдың меншікті ішкі энергиясы өзгермейді (u₂=u₁) Изобаралық процессте n=0 тең болғанда меншікті ішкі энергияұлғаяды. Жылу берумен жүретін изохоралық процессте болғанда меншікті ішкі энергия өседі. Осыдан мынадай қорытынды шығаруға болады,барлық политропты процесстер, яғни кеңею процесстері кезінде, ал сығылу процессі кезінде меншікті ішкі энергияның өсуімен жүреді..

Политропты процессте жылу мөлшері қалай өзгеретінін қарастырайық (3.9). Адибаталық процесстее жыу берілмейді және алынбайды. Изотермиялық процессте (n=1),изобаралық процессте (n=0) кеңейеді және изохоралық процессте 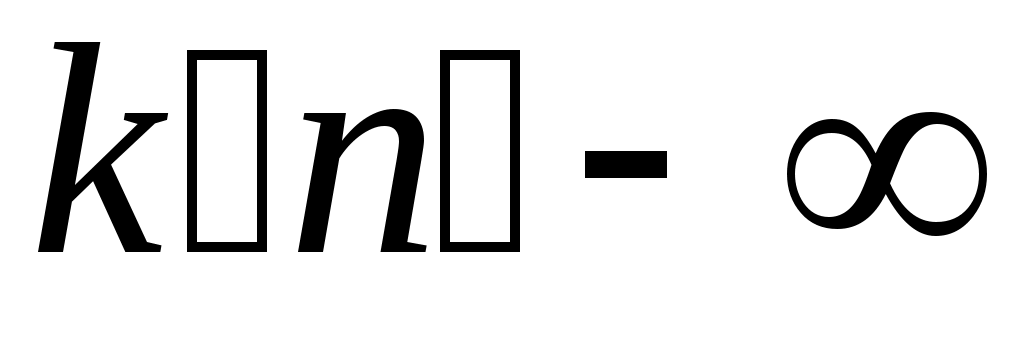жылу беріледі.Осыдан барлық плитропты процесстер, яғни кеңею процесстері шегінде, алсығылу процесстері жылу берумен жүреді.

Адиабатаның және изотерманың арасында орналасқан процесстердің жылу сыйымдылығы теріс мәнді, өйткені 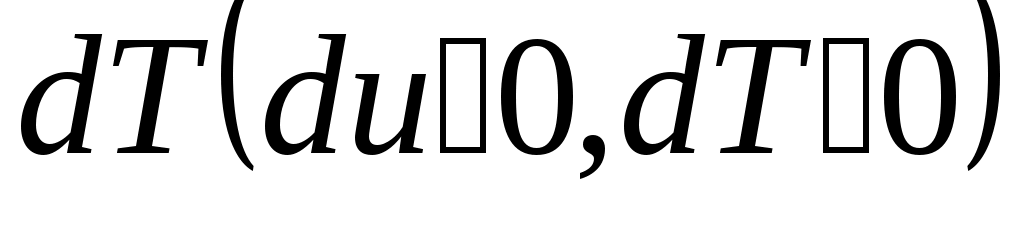және таңбалары бұл процесстерде әр түрлі. және таңбалары мынаған сәйкес келеді: және . Сонда меншікті жылу сыйымдылығының теңдеуінен көріп отырғанымыздай, ол шын мәнінде теріс.

Бұл процесстерде жылу беру кезінде температура төмендейді, ал жылу алынған кезде ұлғаятынын тәжірибеден қөруге болады..