научная статья по математике. Статья 2 Гнутова Е.В.. Е. В. Гнутова (Армавир) Применение алгоритма нахождения наибольшего и наименьшего значений функций
 Скачать 409.28 Kb. Скачать 409.28 Kb.
|
|
Е.В. Гнутова (Армавир) Применение алгоритма нахождения наибольшего и наименьшего значений функций В процессе реализации практической деятельности при обучении математике нередко применяют понятие и поиск производной тогда, когда требуется определить наибольшее и наименьшее значение функции. Люди выполняют данные действия в том случае, когда нужно выяснить, с помощью какого способа довести затратную часть до минимального значения, как значительно осуществить увеличение прибыли, каким образом определить объективную нагрузку на производственное оборудование и т.д., то есть тогда, когда принципиально выяснить оптимальное значение какого-либо управляющего коэффициента. При решении задач данного типа правильным образом, необходимо ясно представлять, чем является наибольшее и наименьшее значение функции. Как правило, в теории и практике обучения математике определяются эти значения в рамках некоторого интервала x, который может определенным образом соотноситься со всей областью определения функции или ее части. Таким интервалом может быть как отрезок [a; b], так и открытый интервал (a; b) , (a ; b ] , [ a ; b ), бесконечный интервал (a ; b) , (a ; b ] , [a ; b), либо бесконечный промежуток (− ∞ ; a) , (− ∞ ; a ] , [a ; + ∞) , (− ∞ ; + ∞). Нам предстоит разобраться с тем, каким образом можно вычислить наибольшее и наименьшее значение функции с одной переменной y=f (x) явно заданной. Представим формулировки основных определений, которые нам пригодятся. 1определение. Наибольшее значение функции y = f (x) на некотором промежутке x– это значение max y = f ( x 0 ) x ∈ X, которое при любом значении x ∈ X , x ≠ x 0, делает справедливым неравенство f ( x ) ≤ f ( x 0 ). 2 определение. Наименьшее значение функции y = f (x) на некотором промежутке x – это значение min x ∈ X y = f (x 0), которое при любом значении x ∈ X , x ≠ x 0 делает справедливым неравенство f(X f x) ≥ f (x 0 ). Представленные формулировки определений представляются нам достаточно прозрачными. Однако можно сформулировать и в упрощенном виде: наибольшее значение функции – это самое большое значение, которое она принимает на определенном интервале при абсциссе x0, а наименьшее – наименьшее принимаемое значение на том же интервале при x0. 3 определение. Стационарными точками называются такие значения аргумента функции, при которых производная функции обращается в 0 (нуль). Для чего нужны все определения, и в частности определение стационарных точек? Чтобы ответить на сформулированный нами вопрос необходимо вспомнить формулировку теоремы Ферма. Из ее содержания следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Целесообразно отметить, функция станет приобретать наименьшее или наибольшее значение на определенном промежутке определенно в одной из стационарных точек. Кроме этого, функция, по-видимому, будет принимать наибольшее или наименьшее значение в тех точках, в которых данная функция определена, а ее первая производная не наличествует. Одно из первых затруднений, с которым сталкивается обучающийся при рассмотрении данной темы,: всегда ли возможно нахождение наибольшего или наименьшего значения функции на выделенном отрезке? Ответ может быть следующим: нет, не всегда. Это зависит от многого, в частности: совпадают ли границы заданного промежутка с границами области определения функции, или область определения функции - бесконечный интервал. Иногда происходит следующее: функция на определенном отрезке или на бесконечности способна принимать бесконечно малые или бесконечно большие значения. Тогда выяснить наибольшее и/или наименьшее значение функции становится не возможным. Разобраться с данными выводами можно проанализировав информацию, представленную на графиках (см. рисунок 1-3): 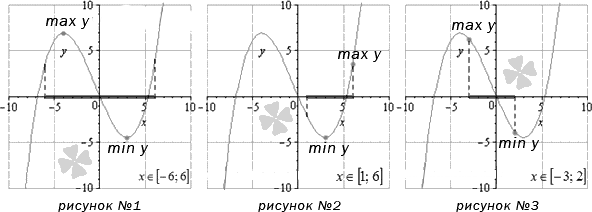 Наибольшее и наименьшее значение функции на отрезке. На рисунке 1 представлен график функции, принимающей наибольшее и наименьшее значения (max y и min y) в стационарных точках, принадлежащих отрезку [-6;6]. Остановимся на втором графике функции и разберем данный пример развернуто. Если переменим значение границ отрезка на [1; 6], то выяснится, что наибольшее значение функция будет достигать в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке. На третьем графике абсциссы точек - граничные точки отрезка [-3; 2]. Они соответственно равны наибольшему и наименьшему значению заданной функции. 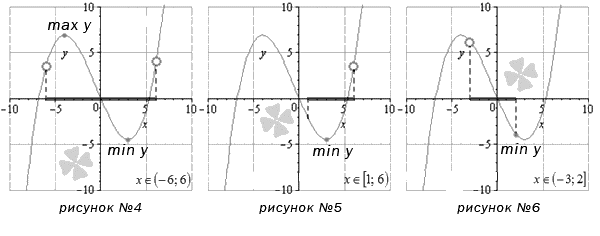 Наибольшее и наименьшее значение функции на открытом интервале. Проанализируем функцию, представленную на четвертом графике (см. рисунок 4). Данная функция приобретает наибольшее значение max y и наименьшее значение min y в стационарных точках на заданном открытом интервале (-6;6). Разберемся с интервалом [1;6), на котором наименьшее значение функции, возможно, будет достигнуто в стационарной точке. При этом значение функции, соответствующее наибольшему, будет неизвестно. Функция может принять наибольшее значение при x, равном 6, при x=6 , а это значение расположено в выделенном интервале. График, изображенный на рисунке 5, соответствует разбираемому нами заданию. На графике функции, изображенном на рисунке 6 , свое наименьшее значение, описываемая нами функция, достигает в правой границе представленного интервала (-3;2], а о том, каким будет наибольшее значение данной функции нельзя сделать определенных выводов. 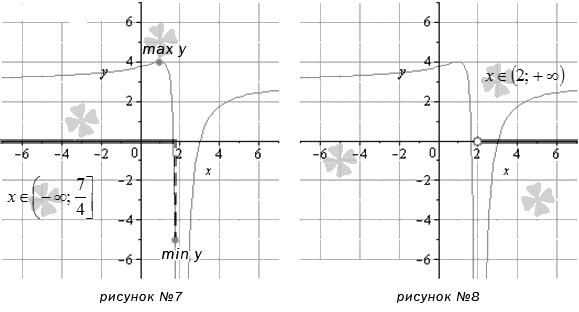 Наибольшее и наименьшее значение функции на бесконечности. Из графика функции, представленном рисунке 7, можно выяснить, что функция будет принимать max y в стационарной точке, с абсциссой, равной 1. Наименьшее значение функция приобретет на границе выделенного интервала с правой стороны. На области определения «минус бесконечности» график функции и ее значения асимптотически приближаются к значению y=3. Рассматривая интервал x ∈ (2; + ∞) , выясним, что предложенная функция не станет принимать на данном интервале ни наименьшего, ни наибольшего значений. При стремлении x 2 , значения функции при этом устремляются к «минус бесконечности», т.к. прямая x = 2 – является вертикальной асимптотой. Если же значение абсциссы устремится к «плюс бесконечности», то значения функции асимптотически приближаются к значению y=3. Наши рассуждения справедливы по отношению к графику, представленному на рисунке 8. Изложим рекомендации для обучающихся по нахождению наибольшего и наименьшего значения непрерывной функции на определенном отрезке. Перед тем как начать применять описанные нами методические рекомендации необходимо вспомнить: каким образом возможно однозначно определить односторонний предел функции и предел функции на бесконечности, а также изучить основные методы их нахождения. При определении наибольшего и (или) наименьшего значения функции на открытом или бесконечном интервале необходимо осуществить пошагово следующую последовательность операций. 1.Убедиться, что заданный интервал является подмножеством области определения данной функции. Выяснить, что все точки, содержащиеся в заданном интервале и в которых не существует первой производной функции. Как правило, они бывают у функций, аргумент которых заключен в знаке модуля, и у степенных функций, содержащих дробно- рациональный показатель. Если такие точки не определены, значит можно переходить ко второму пункту. 2. Выяснить, какие стационарные точки разместятся на определенном промежутке. Надо приравнять производную функции к 0 (нулю), затем решить уравнение и отобрать подходящие корни. В отсутствие стационарной точки или при не попадании их в заданный интервал, следует перейти к следующей процедуре: определению вида интервала. Если интервал имеет вид [a; b), возникает необходимость определения значения функции в точке x=a и односторонний предел limx→b-0 f (x). Если интервал имеет вид ((a; b], то потребуется выяснить значение функции в точке x = b и односторонний предел lim x → a + 0 f (x).Когда интервал имеет вид (a; b), то необходимо определить односторонние пределы lim x → b – 0 f (x), lim x → a + 0 f (x). Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x = a и предел на плюс бесконечности lim x → + ∞ f (x). Если интервал выглядит как (-∞; b], то определим значение в точке x = b и предел на минус бесконечности lim x → − ∞ f (x) . Если ( − ∞ ; b ) , то рассчитаем односторонний предел lim x → b − 0 f (x) и предел на минус бесконечности lim x → − ∞ f (x). Если же (− ∞ ; + ∞) , то рассчитаем пределы на «минус- бесконечности» и «плюс -бесконечности» lim x → + ∞ f (x) , lim x → − ∞ f (x). В конце, после анализа полученных значений функции и пределов, потребуется осуществить вывод. В этом случае предоставляется возможность реализации множества вариаций. Например, если односторонний предел равен «минус бесконечности» или «плюс бесконечности», то, по всей видимости, о наименьшем и наибольшем значении функции ничего нельзя сказать определенного. Остановимся на разборе последовательности действий по решению типичного примера. Подобные алгоритмы действий позволит применить это на практике и сформировать необходимый навык. Если будет потребность, есть возможность рассмотреть дополнительно графики функций, изображенные на рисунках 4 − 8 данного материала. Здесь нами представлена система последовательных действий, которую необходимо воспроизвести для нахождения наибольшего или наименьшего значения функции на некотором отрезке. Для начала найти область определения функции. Выяснить, входит ли в нее заданный в условии отрезок. Теперь вычислить точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего они встречаются у функций, аргумент которых находится под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом. Затем выяснить, какие стационарные точки попадут в заданный отрезок. Для этого потребуется вычислить производную функции, затем приравнять ее к 0(нулю) и решить получившееся в итоговое уравнение, после чего отобрать подходящие корни. Если у не определяются ни одной стационарной точки или они не попадают в заданный отрезок, необходимо выполнить следующий шаг. Выяснить, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычислить значения для x=a и x=b. В результате получится ряд значений функции, из которых теперь нужно отобрать самое большее и самое меньшее. Это и будут наибольшее и наименьшее значения функции, которые требовалось найти. Очевидно, что если рационально применять этот алгоритм при решении задач на нахождение наибольшего и наименьшего значения функции, то результат обучения математике будет соответствовать тому, который заявлен в ФГОС по данной теме. Литература Могильницкий, В. А. Производная и ее применение: учебное пособие / В.А. Могильницкий, С. А. Шунайлова. – Челябинск: Издательский центр ЮУрГУ, 2011. – 107 с. |
