Решение электродинамика. Бабенко примеры задач. Электродинамика и распространение радиоволн упражнения и задачи
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Волны в прямоугольном волноводеРешение однородного скалярного уравнения Гельмгольца 2Для этих функций Т(x,y) и Z(z) справедливы уравнения d2Z dz2 + Г2 Z = 0, 2T + 2 T = 0. 2 = k2 – Г2. Введено обозначение 2 = 2/ x2 +2/y2. Использованный прием решения называется методом разделения переменных. Решение дифференциального уравнения для Z(z) можно записать в форме Z (z)= При этом По форме два члена решения – комплексные амплитуды волн. Это неоднородные волны, так как их амплитуды зависят от поперечных координат x, y. Если Г – вещественная величина, то она играет такую же роль, как k – волновое число. При комплексном Г = Г ’ – i Г ” (Г ’, Г ” > 0) имеем Г ’= / vф = 2 / , где - длина волны, vф – ее фазовая скорость, Г ”- коэффициент затухания. Величина Г называется продольным волновым числом, или постоянной распространения. Параметр - поперечное волновое число. Не известны функция T(x,y) и параметр 2. Само по себе уравнение 2T + 2 T = 0 не имеет определенных решений. Необходимо поставить краевую (граничную) задачу. Например, если задать на контуре L обобщенного цилиндра T = 0, будет сформулирована задача Дирихле. Предположим, что задача внутренняя, т.е. решение Т ищется внутри обобщенного цилиндра. Тогда задача имеет бесконечное множество решений Тn, каждое из которых реализуется при определенном значении параметра 2. Решения Тn называются собственными функциями, а соответствующие им значения n2 параметра 2 – собственными значениями. Если разным собственным функциям соответствуют одинаковые собственные значения, то последние называются вырожденными. Если на контуре L задано T / n = 0 – то это краевая задача Неймана. Это задача также порождает систему собственных функций, которым отвечают собственные значения. В продольно однородной структуре поперечные компоненты поля (составляющие векторов, лежащие в поперечной плоскости сечения структуры) и продольные компоненты (совпадающие с направлением вдоль структуры) связаны соотношениями. Индекс () употреблен в качестве знака отсутствия производных по z. Волна, переносящая энергию в направлении z , обязательно должна иметь как поперечную электрическую При этом достаточно, чтобы электромагнитное поле имело только одну продольную компоненту – либо Нz, либо Ez. Общее решение может рассматриваться как наложение двух частных, для одного из которых Ez 0, Нz = 0 – класс Е- волн, или электрических волн (ТМ - волны), а для другого Нz 0, E z= 0 – класс Н- волн, или магнитных волн (ТЕ – волны). Волновые процессы, имеющие как электрическую, так и магнитную продольные компоненты, называют гибридными волнами. Простейшая электромагнитная волна в свободном пространстве, которая является продольно однородной структурой, лишена продольных компонент (Ez= 0, Н z = 0). Она относится к классу Т- волн (ТЕМ- волн – поперечно-электромагнитные волны). Существование таких волн возможно при 2 = 0. При этом Г = k, т.е. любые Т- волны распространяются в среде с той же фазовой скоростью, что и плоская однородная волна. В отличие от Т- волн для всех остальных волновых процессов Г = (k2 - 2) 1/2 . Если рассматривать незатухающие волны, для которых Г – вещественная величина, то при 2 > 0 Г < k, фазовая скорость рассматриваемой волны vф > v – больше скорости Т – волны в рассматриваемой среде. Это быстрые волны. При 2 < 0, т.е. при мнимых поперечных волновых числах, vф < v – это медленные волны. В прямоугольном волноводе с идеально проводящей оболочкой могут существовать только волны классов Е- и Н-. Так как поперечные составляющие векторов поля выражаются через продольные, то для вычисления поля этих волн достаточно определить составляющую Е – волны. 2z x2 +2z y2 +2 z = 0, z = 0 на прямоугольном контуре L. Это - краевая задача Дирихле. Задача решается методом разделения переменных z =X (x) Y(y). Продольная составляющая электрического поля zmn (x,y) = E0mn sin(mx/a) sin(ny/b); mn2 = (m / a)2 + (n / b)2. Разным значениям m, n соответствуют разные типы колебаний (разные моды) m = 1, 2, 3,… n = 1, 2, 3,… Значения m = 0, n = 0 не годятся, так как в этом случае z = 0 во всех точках внутри волновода. Для нахождения постоянной E0mn требуются дополнительные данные, например, более конкретные сведения об источнике, создающем рассматриваемую волну. Продольное волновое число Гmn= k [1- (fкрmn / f)2]1/2 = k [1 – ( крmn)2]1/2, критическая частота для определенного типа колебаний fкрmn = [c/2(rr )1/2][(m /a)2 + (n /b)2]1/2, крmn= 2/ [(m /a)2 + (n /b)2]1/2 - критическая длина волны. ZmnE = Г mn/( Н – волны. В этом случае требуется решение второй краевой задачи для z. На стенках волновода граничные условия: z / x = 0 при x = 0, a, z / y = 0 при y = 0, b. Результат решения этой краевой задачи zmn = H0mn cos (mx/a) cos (ny/b); mn2 = (m / a)2 + (n / b)2. m = (0), 1, 2, … n = (0), 1, 2, … В случае H– волн m и n могут принимать нулевые значения. Однако они не могут равняться 0 одновременно: при этом составляющая z не зависит от переменных x и y и вектор электрического поля будет тождественно равен 0, что невозможно. H0mn - неопределенная постоянная. Постоянная распространения Гmn, критическая частота fкрmn и критическая длина волны крmn такие же, как для волн класса Е. Волновое сопротивление в Н- классе ZmnH = 0r Гmn= Zc0 [1- (fкрmn / f)2] - 1/2 = Zc0[1 – ( крmn)2]- ½, Zc0 =120 (r /r)1/2. Структура поля в поперечном сечении (при фиксированном значении координаты z) аналогична структуре стоячей волны. Индекс m равен числу полуволн (x/2=a/m), укладывающихся на поперечном размере «а» стенки, параллельной оси х. Индекс n равен числу полуволн (y/2=b/n), укладывающихся на поперечном размере «b» стенки, параллельной оси y. Равенство 0 одного из индексов означает, что поле рассматриваемой волны не зависит от соответствующей координаты. Распространение волны происходит только, если постоянная распространения волны Гmn – вещественная, т.е. при < крmn. Длина волны в волноводе определяется продольным волновым числом Гmn 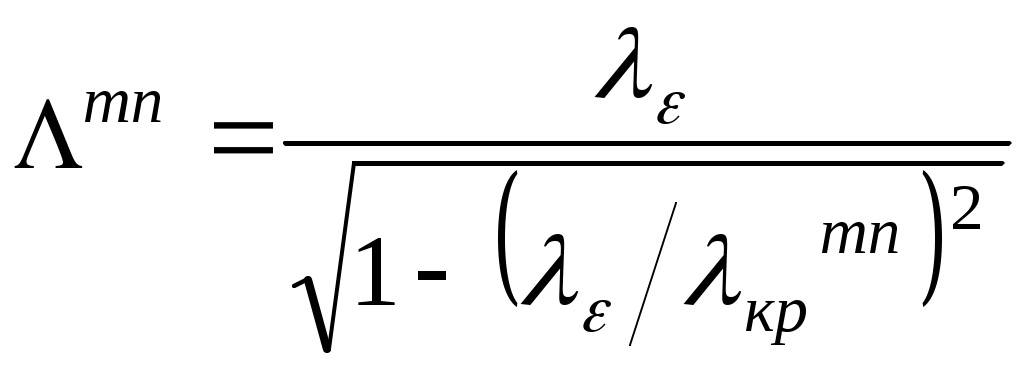 . Здесь . Здесь 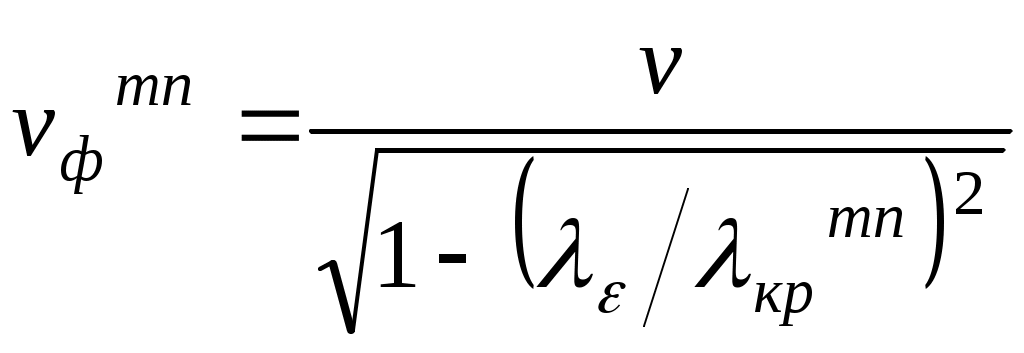 , а групповая скорость, или скорость переноса энергии , а групповая скорость, или скорость переноса энергии Для различных типов волн критическая длина волны зависит от размеров а и b и от индексов m и n. При увеличении значений индексов и фиксированных размерах волновода значение крmn уменьшается. Наибольшую критическую длину при a > b имеет волна Н10. кр10=2а. Волну, имеющую наибольшую крmn, называют основной волной рассматриваемой линии передачи (или волной низшего типа). При a > b, основной волной прямоугольного волновода является волна Н10. При фиксированной частоте f только для некоторых достаточно малых m и n выполняется условие f > fкр ( fкрmn =[ c/ [2 (rr)1/2]] [(m /a)2 + (n /b)2]1/2 ), лишь для конечного числа типов Гmn вещественное и только эти типы имеют характер распространяющейся волны, переносящей энергию. Если а > b, волна Н10 - волна с наименьшей критической частотой fкрmin = f кр10 = [c /(rr)1/2] (1/2a). Отличительное свойство основной волны – однородность поля в направлении оси у. Если частота сигнала f > fкр10 (т.е. больше критической для основного типа), но меньше критической частоты любого высшего типа f < fкрmn, то только основной тип будет распространяющимся. Такой режим работы волновода называется одноволновым (одномодовым). Если размер a 2b, то ближайшим высшим типом будет Н20.
Одномодовый режим обеспечивается в диапазоне частот f1 = c/2a и f2 =c/a, отношение которых равно 2, т.е. ширина рабочего диапазона составляет одну октаву. з   апредельный рабочий диапазон многомодовый апредельный рабочий диапазон многомодовый(одномодовый)     0 H10 H20 H01 H11, E11 Рабочий диапазон для одномодового режима a< <2a . Рассмотрим пример. Сигнал с несущей частотой 30 ГГц передается по волноводу прямоугольного сечения 7.2 × 3.4 мм2. Длина волновода L=10 м. Определить время задержки. Как изменится фаза несущей, если волновод удлинить на L=1 мм? Длина волны в воздухе («рабочая» длина волны) Критическая длина волны основного типа колебаний Заданы такие размеры волновода (a>2b), что ближайшим типом колебаний будет мода с индексами (20): Длина волны в волноводе 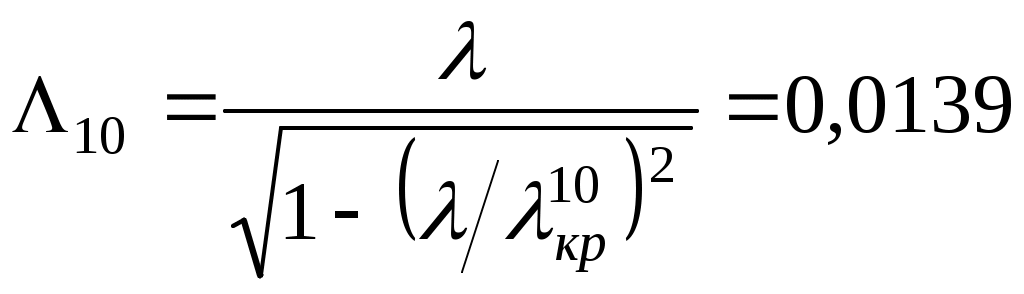 м (больше, чем длина волны в свободном пространстве). Время задержки сигнала определяется скоростью переноса энергии по волноводу, т.е. групповой скоростью м (больше, чем длина волны в свободном пространстве). Время задержки сигнала определяется скоростью переноса энергии по волноводу, т.е. групповой скоростьюИзменение фазы несущей – это изменение показателя в сомножителе Элементарный электрический излучатель. Элементарный электрический вибратор – это настолько малый элемент объема Dv = lDs, выделенный в области, где расположены сторонние источники, что комплексная амплитуда плотности тока в нем практически постоянна, а размеры малы по сравнению с длиной волны. Амплитуда и фаза тока не изменяются вдоль него. Приближенной физической моделью такого элементарного излучателя может служить так называемый диполь Герца. П 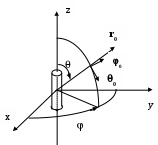 усть вибратор, расположенный в безграничной однородной изотропной среде, ориентирован вдоль оси z. Расположим начало координат в его средней точке. Ток в вибраторе Iст = Imст cos wt. усть вибратор, расположенный в безграничной однородной изотропной среде, ориентирован вдоль оси z. Расположим начало координат в его средней точке. Ток в вибраторе Iст = Imст cos wt.Предполагается,l << r, l<< l - элемент должен быть мал по сравнению с расстоянием наблюдения и мал в волновом масштабе Выражения для комплексных амплитуд векторов поля 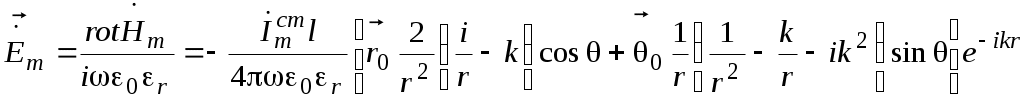 Вектор напряженности электрического поля имеет две составляющие Еq и Еr, вектор напряженности магнитного поля имеет одну компоненту Нj. Таким образом в любой точке пространства вектор При анализе структуры электромагнитного поля излучателя пространство вокруг него обычно делят на три зоны: дальнюю или волновую (kr>>1), ближнюю (kr<<1) и промежуточную. Поле в ближней зоне. Здесьr<< l, следовательно, можно считать exp(-ikr) »1 и оставить в выражениях соответствующие слагаемые (1/ r n) с учетом их малости. Распределение электрического поля такое же, как и в случае электростатического диполя. Однако поле переменно во времени и изменяется по закону cos (wt+ y). Выражение для напряженности магнитного поля совпадает с формулой закона Био –Савара (где I – ток в вибраторе в рассматриваемый момент времени). Таким образом, в ближней зоне преобладает квазистационарное поле. Эта зона индукции. Вектора Заметим, что в случае среды без потерь полные потоки энергии в ближней и дальней зонах одинаковы, а плотность потока энергии в ближней зоне значительно больше, чем в дальней. В дальней зоне, на расстояниях r >> l, основную роль играют слагаемые, содержащие множитель [exp(-ikr)]/r. Поле в дальней зоне имеет характер сферической волны с постоянной распространения k= w / c = 2 p/l. Электрические и магнитные компоненты синфазны. Синфазность векторов 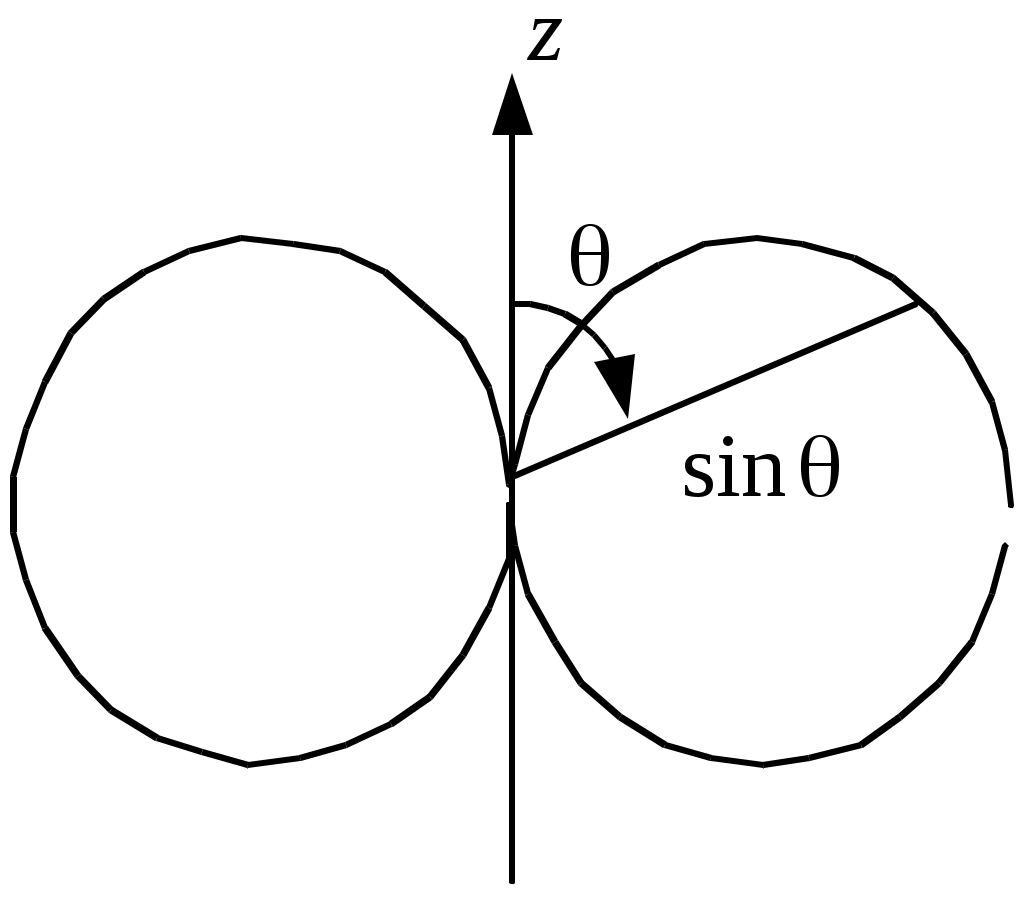 Волна неоднородна: поверхности равных амплитуд определяются уравнением sinq/r=const и не совпадают с поверхностями равных фаз. Поле содержит только поперечные составляющие Нj и Еq, которые взаимно перпендикулярны и перпендикулярны направлению распространения волны (нет компонент нормальных поверхности фазового фронтаr = const, т.е. поле может быть отнесено к классу Т). Связь между векторами Промежуточная зона является переходной от ближней зоны к дальней. При анализе выражений в этом случае нельзя пренебречь ни одним из слагаемых. Следовательно, в промежуточной зоне поле излучения и реактивное (связанное с вибратором) поле оказываются одного порядка. Рассмотрим пример. Н 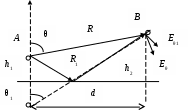 а высоте h1 над поверхностью земли расположен элементарный электрический излучатель А, ориентированный вдоль нормали к поверхности. Определить вектор напряженности электрического поля в точке В, расположенной на высоте h2. Расстояние d>> . а высоте h1 над поверхностью земли расположен элементарный электрический излучатель А, ориентированный вдоль нормали к поверхности. Определить вектор напряженности электрического поля в точке В, расположенной на высоте h2. Расстояние d>> .Поле в точке В является суперпозицией полей двух волн: прямой волны от источника в направлении Известно, что вектор напряженности электрического поля элементарного излучателя имеет в дальней зоне (d>> ) только одну составляющую: Следовательно, можно записать ЗдесьR|| - коэффициент отражения Е - поляризованной волны, учитывающий изменение комплексной амплитуды вектора Вектора где 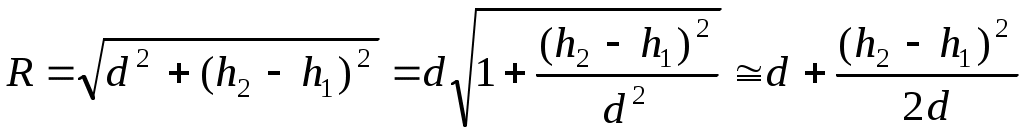 , ,При этом множитель F, учитывающий влияние земли Если землю рассматривать как идеальный проводник, R|| = 1, тогда модуль Е 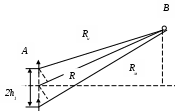 сли в условии задачи изначально говорилось бы об идеально проводящей поверхности, задачу можно решить, используя метод зеркального изображения: рассматривать искомый вектор поля как результат суперпозиции поля заданного источника и поля зеркального изображения этого источника – вертикального излучателя. Токи в обоих излучателях равны по величине и совпадают по фазе. сли в условии задачи изначально говорилось бы об идеально проводящей поверхности, задачу можно решить, используя метод зеркального изображения: рассматривать искомый вектор поля как результат суперпозиции поля заданного источника и поля зеркального изображения этого источника – вертикального излучателя. Токи в обоих излучателях равны по величине и совпадают по фазе. Учитывать, что расстояния Rи .иRм различны и отличаются от R – расстояния от точки пересечения нормали с поверхностью раздела, следует только в фазовых множителях (в показателях экспонент), так как разговор идет об определении поля в дальней зоне. Rи = R – h1cosθ, Rм = R + h1cosθ. = Упражнения и задачи Векторный анализ Ф1. Показать, что в неоднородной среде, магнитная проницаемость которой есть функция пространственных координат, вытекает следующее уравнение для вектора напряженности магнитного поля: div H = - 1 / μ a (H grad μ a) Ф2. Подсчитать циркуляцию вектора А = - х 0у / а +у 0х / а по окружности х 2 + у 2 = а 2 . Ф3. Даны два вектораA = 3x0 + 4y0 +5z0R =xx0 + yy0 + zz0 Определить grad ( AR) Ф4. Задан потенциал φ = xy + z 2 . Найти gradφ в точке с координатами x = 2.7; y =2; z = 2. Ф5. Определить поток вектора Ф6. Используя представление дивергенции как поток вектора сквозь замкнутую поверхность, составить выражение для Ф7. Определить ротор векторного произведения заданного вектора А и радиус-вектора R. Ф8. Найти лапласиан скаляра Электростатика Э1. Определить вектор напряженности электрического поля линейного протяженного источника. Э2. Определить вектор напряженности электрического поля, создаваемого бесконечной плоскостью, по которой распределен заряд с поверхностной плотностью s. Э3. Найти вектор напряженности электрического поля на оси диска радиуса b, по которому распределен заряд с поверхностной плотностью s. |
