Решение электродинамика. Бабенко примеры задач. Электродинамика и распространение радиоволн упражнения и задачи
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Э4. Найти вектор напряженности электрического поля на оси линейного источника длины L.Э5. Положительный заряд Q расположен в центре сферической полости радиуса Ri в проводящей сфере радиуса R0. Определить вектор напряженности электрического поля и скалярный потенциал, как функцию расстояния R. Э6. Положительный заряд Q расположен в центре сферической полости радиуса Ri в диэлектрической сфере радиуса R0. Определить вектор напряженности электрического поля и скалярный потенциал, как функцию расстояния R. Э7. Две металлические сферы радиусов b1 и b2 соединены проводником. Суммарный заряд, сообщенный сферам, равен Q. Расстояние между сферами велико настолько, что распределение заряда на них можно считать равномерным. Найти: а) заряд на каждой из сфер, б) вектор напряженности электрического поля на поверхности каждой сферы. Э8. Цилиндрический конденсатор состоит из внутреннего проводника радиуса a и внешнего проводника, внутренний радиус которого b. Пространство между проводниками заполнено диэлектриком с проницаемостью r. Длина конденсатора L. Определить емкость конденсатора. Э9.Две проводящие полуплоскости ортогональны. Заряд Q находится на расстоянии d1 от одной и d 2 от другой из них. Определить силу, действующую на заряд. Э10.Плоская граница раздела двух сред с диэлектрическими проницаемостями εr 1 и εr2 свободна от зарядов. Известно, что вектор напряженности электрического поля Е1 составляет угол φ1 с нормалью к границе раздела. Определить Е 2 и φ2. Э11.В вакууме на одной прямой расположены три точечных заряда: q1 = 2 мкКл, q2 = 7 мкКл и q3 = 10 мкКл. Определить напряженность электрического поля в точке 0. 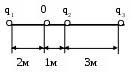 Э 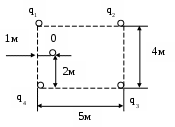 12. В вакууме расположены четыре точечных заряда: q1 = 1 мкКл, 12. В вакууме расположены четыре точечных заряда: q1 = 1 мкКл, q2 = - 2 мкКл и q3 = 3 мкКл и q4 = - 4 мкКл. Найти напряженность электрического поля в точке 0. Э13.Тонкий кольцевой проводник радиусом 1 см несет полный заряд 1 мкКл. Определить напряженность электрического поля и скалярный потенциал в точках на оси кольца. Э14.Равномерно заряженный диэлектрический шар (r = 10) находится в однородной диэлектрической среде (r = 4). Найти напряженность поля на поверхности шара и на расстоянии 2R от центра. R= 0,5 м, = 2 мкКл/м3. Э15. Имеется нить, заряженная с погонной плотностью 10 Кл/м. Найти напряженность электрического поля в точке, расположенной на расстоянии 10 см от оси нити в случае двух диэлектриков: r = 4 и r = 10. Э16.Определить вектор напряженности электрического поля в точке Р (-0.2, 0, -2,3), которое создает заряд Q = 5нК, расположенный в точке Q(0.2, 0.1, -2.5). Э17. В толщине однородного диэлектрика первоначально создано равномерное электрическое поле, затем прорезаны две узкие полости, одна из которых ориентирована параллельно, а другая перпендикулярно вектору E. Полости заполнены воздухом. Какова величина напряженности электрического поля в обеих полостях? Э18. Диэлектрическая пластина размещена в однородном электрическом поле ортогонально вектору напряженности электрического поля. Определить Е и D в пластине. Э19. Определить скалярный потенциал в пространстве между пластинами плоского конденсатора и плотность поверхностного заряда на пластинах. Э20. Поверхность бесконечно длинного кругового цилиндра равномерно заряжена так, что на единицу длины приходится заряд . Определить поле внутри и вне цилиндра, скачек вектора Е при прохождении через заряженную поверхность цилиндра, потенциал поля заряженного цилиндра. Э21. Определить напряженность поля в полости цилиндрического конденсатора (два коаксиальных цилиндра), если - заряд единицы длины внутреннего цилиндра. Определить емкость цилиндрического конденсатора. Э22. Положительный заряд q равномерно распределен по объему шара радиуса а. Найти Е, D и вне и внутри шара. Задачу решить, используя теорему Гаусса и с помощью уравнения Пуассона-Лапласа для скалярного потенциала. Стационарное магнитное поле М1. По бесконечно длинному прямому проводу радиуса b, находящемуся в воздухе, течет ток I. Определить вектор напряженности магнитного поля внутри и вне проводника. М2. По отрезку провода длиной 2L, находящемуся в воздухе, протекает постоянный ток I. Найти вектор магнитной индукции в точке, расположенной на расстоянии r от провода в плоскости, перпендикулярной отрезку и проходящей через его центр. Задачу решить, используя векторный потенциал. М3. Найти вектор магнитной индукции в центре квадратной петли, по которой протекает постоянный ток I. Сторона квадрата 2L. М4. Используя закон Био-Савара, определить вектор напряженности магнитного поля на оси кольцевого проводника, по которому протекает постоянный ток I. М5. Определить индуктивность на единицу длины соленоида, считая, что на единицу длины приходится n витков проводника. Поперечное сечение соленоида S. М6. В среде 1 (магнитная проницаемость r1) известен вектор напряженности магнитного поля в точках на поверхности раздела двух сред (длина вектора H1, угол с нормалью к границе раздела 1) Определить вектор напряженности магнитного поля во второй среде (длину вектора и угол, который он образует с нормалью к границе раздела). Магнитная проницаемость второй среды r2. М7. Вывести выражение для напряженности магнитного поля в коаксиальном кабеле. Радиус внутреннего проводника a1, радиусы внешнего проводника a, a2 , (a2 - внешний радиус кабеля). Задачу решить, воспользовавшись уравнением Максвелла. М8. Вывести выражение для напряженности магнитного поля в коаксиальном кабеле. Радиус внутреннего проводника a1, радиусы внешнего проводника a, a2 , (a2 - внешний радиус кабеля). Задачу решить при помощи уравнения Пуассона – Лапласа для векторного потенциала. М9.Бесконечный прямолинейный проводник с током 1 мА находится в пространстве с параметрами r = 10, r = 1. Найти вектор магнитной индукции на расстоянии 5 м от оси тока. М10.Определить поток энергии через поверхность бесконечного цилиндрического провода, по которому течет постоянный ток I. М11. Вычислить магнитную энергию, сосредоточенную внутри единицы длины цилиндрического провода. М12. Граница раздела сред обладает свойствами экранирования, так что поле в среде 1 может существовать, не проникая в среду 2. (E2 = 0, B2 = 0). Определить поведение векторов поля в среде 1 вблизи границы. М13. Найти энергию магнитного поля и магнитный поток в коаксиальном кабеле (на погонный метр длины кабеля). |
