Решение электродинамика. Бабенко примеры задач. Электродинамика и распространение радиоволн упражнения и задачи
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
|
Система уравнений и общие понятия электростатики. Электростатическое поле описывается системой уравнений, которая получается из системы уравнений Максвелла в предположении, что векторы поля не зависят от времени и отсутствует перемещение зарядов ( Дифференциальная форма уравнений: и интегральная форма: Так как для электростатического поля Вектор Физический смысл имеет разность потенциалов в двух точках – она определяет работу при перемещении единичного заряда в электростатическом поле между этими точками. 1 - 2 = 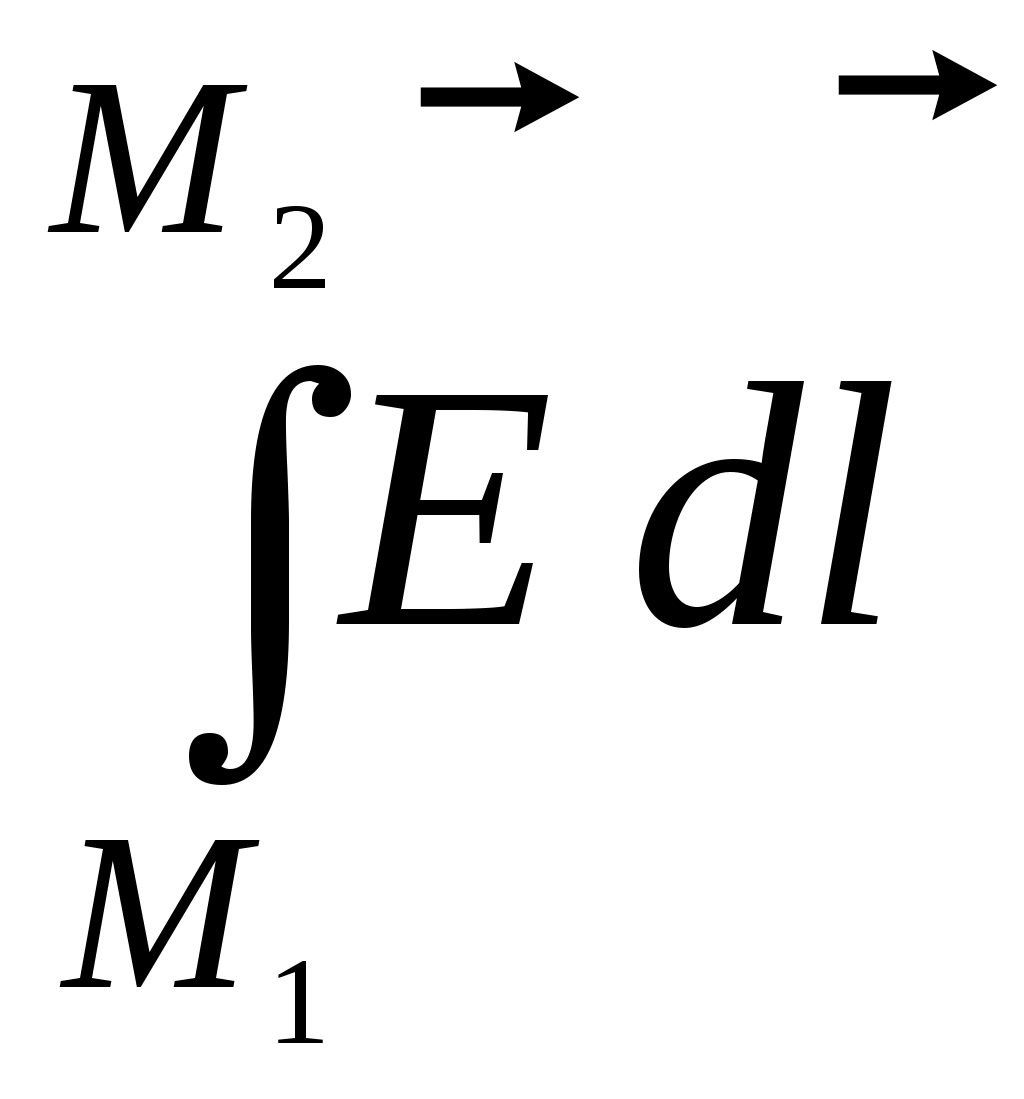 . .Работа электрических сил не зависит от пути перемещения заряда, а определяется только положением начальной и конечной точек – это важнейшее свойство электростатического поля. (Это справедливо для любых потенциальных полей). Если точки совпадают, то Если потенциал бесконечно удаленной точки считать равным 0, то потенциал в точке М можно определить как работу, которую надо совершить для перемещения единичного заряда из точки М, для которой он определяется, на бесконечность. Уравнение для потенциала : = - / 0 r - уравнение Пуассона. Решение этого уравнения имеет вид ( 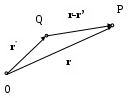 = =В частном случае, когда в рассматриваемой области пространства заряд отсутствует ( = 0), получаем уравнение Лапласа Δ φ = 0. Решения этого уравнения называются гармоническими функциями. Электростатическое поле – частный случай электромагнитного, поэтому приведенные ранее граничные условия для векторов Граничные условия для потенциала . ( )1 = ( )2, где - означает дифференцирование по любому направлению в плоскости, касательной к поверхности раздела в рассматриваемой точке. 1 = 2. 0 r 2 ( n)2 - 0 r 1 ( n)1 = s, n – дифференцирование по нормали к поверхности раздела, направленной из среды 2 в 1. Если одна из сред – проводник, граничные условия принимают более простой вид. Вектор Согласно условию Поверхность проводника в электростатике заряжена ( Из соотношения Примеры расчета электростатических полей. 1.Определим электрическое поле, создаваемое точечным зарядом Q, расположенным в безграничной среде, у которой r – скалярная постоянная (r =const). Такую среду называют однородной и изотропной по отношению к электрическому полю. а).Согласно закону Кулона сила, с которой точечный заряд Q действует на точечный заряд q, Заметим, что часто встречающийся множитель б). Воспользуемся теоремой Гаусса для определения поля точечного заряда. Предположим, что заряд расположен в начале координат. Задача имеет сферическую симметрию (нет предпочтительных направлений), следовательно, в качестве поверхности интегрирования можно выбрать сферу произвольного радиуса. Очевидно, что вектор Следовательно Если заряд находится в произвольной точке пространства, то поле, создаваемое зарядом Q в точке Р будет определяться соотношением 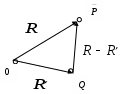 , где , где в). Если заряд распределен по объему равномерно с плотностью , то напряженность поля, создаваемая в точке Р элементом объема dv 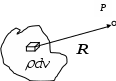 Аналогичные соотношения можно записать, если заряд равномерно распределен по некоторой поверхности с плотностью 2.Вычислим потенциал для точечного заряда, зная его поле 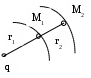 1 - 2 = 1 - 2 =  = = 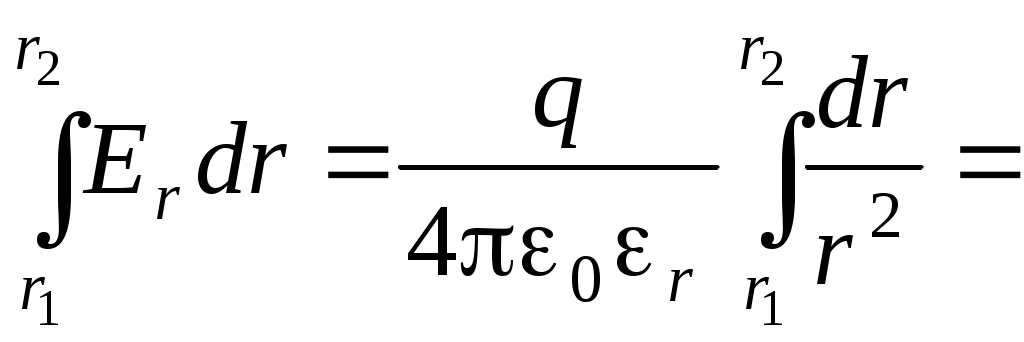 При r2 = Е  сли перенести заряд из точкиr = 0 в точку Q ( сли перенести заряд из точкиr = 0 в точку Q (величина В случае системы точечных зарядов, расположенных в однородной изотропной среде, по принципу суперпозиции 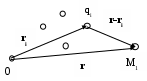 ( (3. Поле электрического диполя. Электрический диполь – система двух близко лежащих равных по величине разноименных точечных зарядов +q и - q. Диполь характеризуется дипольным моментом 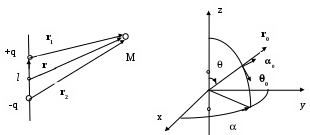 Потенциал диполя найдем по принципу суперпозиции как сумму потенциалов зарядов (+q) и (-q). М = |
