Решение электродинамика. Бабенко примеры задач. Электродинамика и распространение радиоволн упражнения и задачи
 Скачать 1.51 Mb.
|
|
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ РАДИОФИЗИЧЕСКИЙ ФАКУЛЬТЕТ КАФЕДРА РАДИОФИЗИКИ Л.А.Бабенко ЭЛЕКТРОДИНАМИКА И РАСПРОСТРАНЕНИЕ РАДИОВОЛН УПРАЖНЕНИЯ И ЗАДАЧИ Учебное пособие 2006 Содержание Предварительные замечания…………………………………………………….3 Некоторые операции векторного анализа………………………………………6 Немного о векторах и криволинейных системах координат……………7 Градиент скалярного поля………………………………………………..10 Дивергенция векторного поля……………………………………………12 Ротор (»вихрь») векторного поля………………………………………..15 Система уравнений и общие понятия электростатики………………………..18 Стационарное магнитное поле………………………………………………….26 Плоские электромагнитные волны……………………………………………..30 Поляризация волн………………………………………………………...36 Волновые явления на границе двух сред………………………………..37 Волны в прямоугольном волноводе……………………………………………41 Элементарный электрический излучатель……………………………………..48 Упражнения и задачи……………………………………………………………54 Векторный анализ………………………………………………………...54 Электростатика……………………………………………………………54 Стационарное магнитное поле…………………………………………...57 Плоские электромагнитные волны………………………………………59 Волноводы………………………………………………………………...62 Излучение волн……………………………………………………………64 Нет лучшего метода сообщения уму знаний, чем метод преподнесения их в возможно более разнообразных формах. Максвелл Предварительные замечания Классическая, или максвелловская, теория электромагнитного поля учитывает только макроскопические свойства вещества: предполагается, что размеры рассматриваемой области пространства и расстояние от источников поля до рассматриваемой точки велики по сравнению с размерами молекул, а характерное для изменения электромагнитного поля время (например, период колебаний) велико по сравнению со временем, характерным для внутримолекулярных колебательных процессов. Электромагнитное поле описывают следующие векторные функции координат и времени:  – напряженность электрического поля [B/м],  – напряженность магнитного поля [A/м],  – электрическая индукция [Кл/м2],  – магнитная индукция [Tл]. Электрический заряд q (или Q) – фундаментальное свойство вещества. Существуют положительные и отрицательные заряды. Заряд дискретен. Наименьший по абсолютной величине отрицательный заряд |e| = 1,6 10-19 Кл. В макроскопической электродинамике структура материи игнорируется, среда представляется сплошной, а заряды и токи – непрерывно распределенными в объеме (иногда – на поверхности). Используют понятие плотности заряда , как характеристики источника  , q – заряд малого объема V. Как мал объем? Достаточно мал, чтобы следовать изменению , но большой, чтобы содержать большое число дискретных зарядов. Заметим, что куб с ребром в 1микрон (10-6 м) при объеме V=10-18 м3 содержит 1011 атомов.Если считать, что заряд q принадлежит элементу поверхности S или элементу длины l, то следует определить поверхностную s и линейную l плотность заряда.  ,  Названные плотности заряда являются функциям координат и времени. Изменение заряда во времени – это ток. I = - dq / dt [Кл / с = А]. Ток – функция времени. Он следует через ограниченное пространство. Точечная характеристика – плотность тока проводимости  .  - это ток через единичную площадку, расположенную перпендикулярно направлению тока. Для хороших проводников ток высокой частоты распределен в поверхностном слое, а не по объему. Поэтому определяют поверхностную плотность тока  как ток через единицу длины на поверхности, перпендикулярную направлению движения. Плотность тока и плотность заряда не являются независимыми, они связаны законом сохранения заряда. Из определения следует  ,  Если заряд q, содержащийся в объеме V с поверхностью S, не остается постоянным, значит, поверхность пересекают носители заряда, проходит ток.  Это дифференциальная форма закона. Непрерывные и  связаны по закону точечного соответствия.Напряженность электрического поля  определяют как силу, с которой электрическое поле действует на точечный положительный единичный заряд  или точнее,  Сила, с которой электромагнитное поле воздействует на точечный электрический заряд, зависит не только от величины и местоположения заряда, но и от скорости его движения. Эту силу обычно раскладывают на две: электрическую и магнитную. Электрическая сила не зависит от движения заряда  . Магнитная сила зависит от величины и направления скорости  движения заряда и всегда перпендикулярна ей:  – вектор магнитной индукции, характеризующий силовое воздействие поля, [Тл]. Магнитная индукция численно равна силе, с которой магнитное поле действует на точечный единичный положительный заряд, движущийся с единичной скоростью перпендикулярно линиям вектора .В макроскопической электродинамике векторы  и , и  связаны соотношениями, зависящими от свойств среды. Постоянный коэффициент 0 называется электрической постоянной. Его величина зависит от выбора системы единиц. В системе СИ  (Ф / м)0 – постоянная величина, называемая магнитной постоянной, значение и размерность которой зависят от выбора системы единиц. В системе СИ  (Гн/м).Свойства среды характеризуются параметрами r, r и ( - удельная проводимость среды). Материальные среды обладают электрической проводимостью. Под действием электрического поля в них возникает ток, называемый током проводимости. Его плотность определяется законом Ома в дифференциальной форме:  . Перечисленные уравнения называют материальными, или уравнениями состояния.Все электромагнитные процессы, относящиеся к макроскопической электродинамике, подчиняются законам, впервые сформулированным в виде дифференциальных уравнений Дж. К. Максвеллом и опубликованным в 1873 году. (1)  , (2)  , (3)  , (4)  Все величины, входящие в уравнения, являются функциям координат (радиус-вектора  ) и времени t. Плотность электрического тока и плотность заряда характеризуют распределение источников электромагнитного поля в пространстве и во времени. Уравнения в интегральной форме:  (1’),  (2’) (3’),  (4’).Соотношения, показывающие связь между значениями векторов электромагнитного поля в разных средах у поверхности раздела, называются граничными условиями. На поверхности раздела двух сред должны выполняться следующие граничные условия для нормальных и касательных составляющих векторов: D1n – D2n = rs или  = rs ; В1n –B2n = 0 или  = 0Е1t - Е2t = 0 или  = 0; H1t - H2t = jsn или  .Эти соотношения справедливы для электромагнитных процессов, рассматриваемых в макроскопической электродинамике. Некоторые операции векторного анализа. Формально поля определяются заданием в каждой точке рассматриваемой области пространства некоторой скалярной и векторной величины. Эти величины являются функциями четырех переменных – пространственных координат и времени. Немного о векторах и криволинейных системах координат. Вектор  имеет длину (модуль) и направление.  .  - вектор единичной длины (орт), совпадающий с направлением вектора  Скалярное произведение двух векторов  - скаляр. Если два вектора ортогональны, очевидно, что их скалярное произведение равно 0. При перестановке векторов Векторное произведение двух векторов  - это вектор, абсолютная величина которого равна площади параллелограмма, построенного на векторах и , а направление совпадает с направлением нормали к плоскости, содержащей оба рассматриваемых вектора, и определяется из условия образования правой системы с векторами и . Векторное произведение не коммутативно  .Смешанное произведение векторов  - скаляр. Двойное векторное произведение  .Положение точки в пространстве определяется радиус – вектором 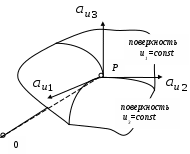 , координаты которого (u1, u2, u3) зависят от принятой системы координат. Положение точки можно однозначно определить пересечением трех поверхностей, семейства которых описываются, как u1=const, u2=const, u3=const. Пересечение двух поверхностей дает координатную линию; значения двух координат на этой линии постоянны, третья меняется. Координаты точки называют криволинейными. Система координат называется ортогональной криволинейной, если касательные к координатным линиям в каждой точке пересекаются под прямым углом. Эти касательные называются координатными осями. Их направление меняется от точки к точке. Пусть  - единичные векторы в трехмерной системе координат. Для правовинтовой ортогональной системы ,  ,  .Вектор, как сумма компонент по трем ортогональным направлениям  ,модуль вектора  .Скалярное произведение векторов    ==  .Векторное произведение 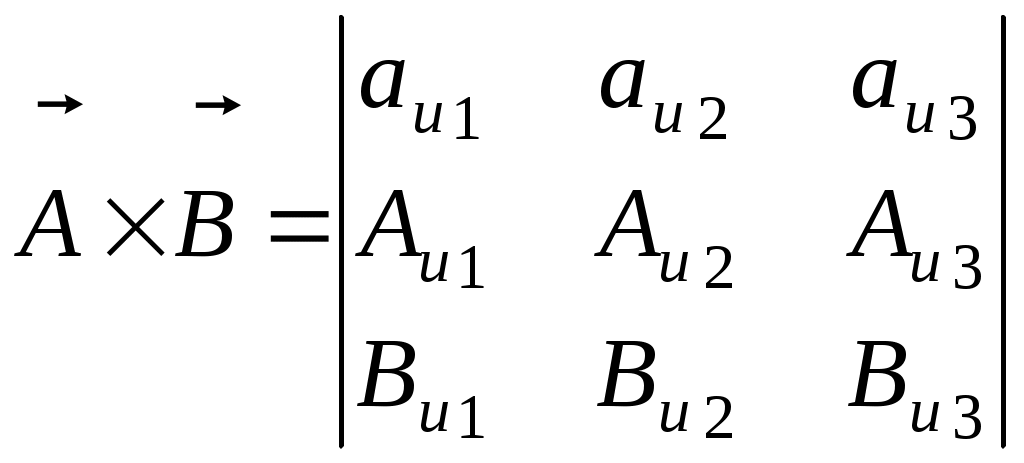 ==  + + /Смешанное произведение векторов 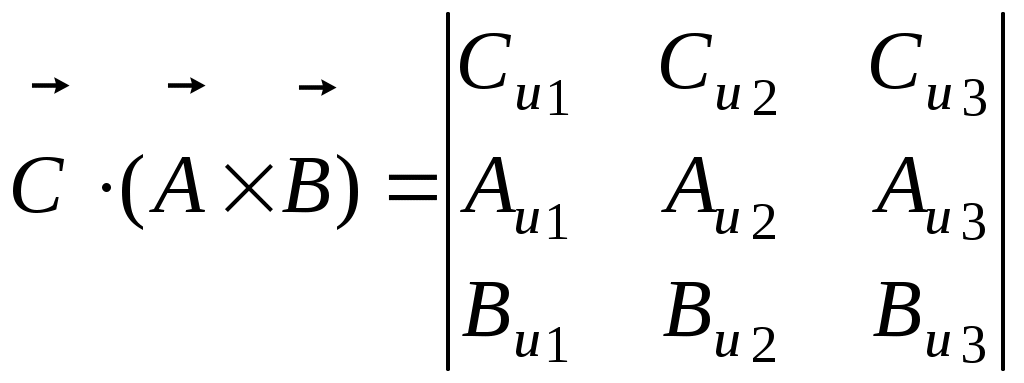 При вычислении линейных, поверхностных или объемных интегралов необходимо вычислить приращения изменения длины через приращения координат. В криволинейной системе координат изменение координаты ui на dui приводит к перемещению dli вдоль координатной линии: dli = hi dui (i = 1,2,3), где hi зависят от вида координат и называются коэффициентами Ламэ. Когда координаты являются длиной, как, например, координаты декартовой системы, эти коэффициенты равны 1. Направленное изменение длины в произвольном направлении можно записать  или .Изменение объема dv, образуемое изменением координат:  К ортогональным криволинейным системам координат относятся прямоугольная (или декартова), цилиндрическая и сферическая система а) Прямоугольные координаты.  Точка Р (x1, y1, z1) определяется пересечением трех плоскостей x = x1,y = y1, z = z1. Радиус – вектор точки Р  .Вектор  .Скалярное произведение  .Коэффициенты Ламэ h1= h2 = h3 = 1. Элемент объема dv = dxdydz Векторный дифференциал длины  .Векторный дифференциал поверхности: 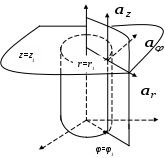  ,  ,  б) Цилиндрические координаты  .Точка Р (r1, φ1, z1) определяется пересечением поверхности цилиндра радиуса r = r1, полуплоскости φ = φ1 и плоскости z= z1. Коэффициенты Ламэ h1 = h3 = 1, h2 = r. Элемент объема dv = rdrdφdz Векторный дифференциал длины  .Векторный дифференциал поверхности:   ,  ,  .в) Сферические координаты  .Точка Р (R1, θ1,φ1) определяется пересечением поверхности сферы радиуса R = R1, поверхности конуса с углом раскрыва 2 θ =2 θ1 и полуплоскости φ = φ1. Коэффициенты Ламэ h1 = 1, h2 = R, h3 = R sinθ. Элемент объема dv = R2 sinθdRdθdφ. Векторный дифференциал длины  .Векторный дифференциал поверхности:  ,  ,  .В векторном анализе производятся специальные операции дифференцирования и интегрирования по отношению к соответствующим функциям пространственных координат. Градиент скалярного поля. Рассмотрим способ описания изменения в пространстве скалярного поля в фиксированное время. По трем пространственным координатам могут существовать частные изменения, причем скорость изменения может быть различной в разных направлениях. Вводят вектор, определяющий скорость изменения скалярного поля в данной точке в данное время. Пусть v (u1, u2, u3) – скалярная функция координат. Величина vзависит от положения точки в пространстве. Вектор, величина и направление которого совпадают с максимальной пространственной скоростью изменения скалярной величины -это градиент этого скаляра.  или  , - орт внешней нормали, направление наиболее быстрого возрастания скаляра v. - набла, или оператор Гамильтона, который можно рассматривать как вектор. Под оператором понимается совокупность математических действий, в данном случае дифференцирование. Сам по себе оператор ничего не означает, он имеет смысл, когда применим к какой-либо величине.   ,  - в декартовой системе координат. Градиент является дифференциальной характеристикой скалярного поля. Пространственное изменение скаляра вдоль направления L:  - пространственная скорость возрастания vв направлении  равна проекции градиента v на это направление.Заметим, скалярное поле v порождает векторное поле  = . Такое векторное поле называется потенциальным полем, функция  – потенциал. Поверхности, на которых v= const, являются эквипотенциальными.Рассмотрим некоторые примеры. 1).Вычислим градиент модуля радиус-вектора  .Модуль этого вектора  . Запишем  .Вычислим частную производную  . Следовательно .2).Вычислим градиент квадрата модуля радиус-вектора.  Запишем соотношение, позволяющее определять градиент модуля радиус-вектора, взятого в произвольной степени n:  . Первые два примера подтверждают правильность приведенного соотношения. Проверим его, предположив, что n = - 1. Вычислим  Дифференциальными характеристиками векторного поля являются дивергенция и ротор. Дивергенция векторного поля. Рассмотрим пространственное изменение векторного поля. Векторное поле графически характеризуется векторными или силовыми линиями. Векторная линия – это кривая, касательная к которой в каждой точке совпадает с направлением векторного поля. Векторные линии характеризуют не только направление, но и величину поля. Плотность их больше там, где величина поля больше. Величина вектора определяется числом линий, проходящих через единичную поверхность, перпендикулярную вектору. Поток поля аналогичен поток жидкости: поток вне, если объем содержит источник. Может быть поток внутрь – если есть сток. Определение: дивергенция векторного поля 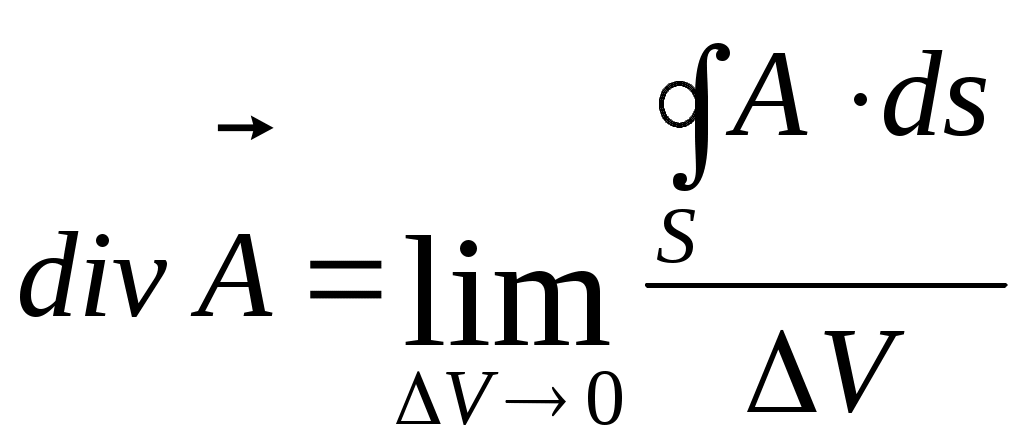 в точке (расходимость вектора)  , s – поверхность, ограничивающая объем  внутри которого находится рассматриваемая точка.  - поток вектора через замкнутую поверхность. Поток может быть больше, меньше или равен 0.  – векторный дифференциал поверхности, направление вектора совпадает с направлением внешней по отношению к поверхности S нормали. исток сток div A = 0, div A > 0, div A < 0 соленоидальное поле поток больше 0 Дивергенция – скалярная величина, значение которой определено в точке.  Для декартовой системы координат  = Ax / x + Ay / y + Az / z. div =  Если дивергенция векторного поля равна 0 div = 0, то – соленоидальное поле. Дивергенция определена как поток вектора через поверхность, ограничивающую единичный объем. Объемный интеграл от дивергенции векторного поля равен полному потоку вектора через поверхность этого объема.  Это теорема Остроградского – Гаусса.Здесь  - векторный дифференциал поверхности – вектор, модуль которого равен ds, а направление совпадает с направлением внешней по отношению к объему dv нормали к элементу ds.Рассмотрим некоторые примеры. 1).Определим дивергенцию радиус-вектора  .В декартовой системе координат радиус-вектор . Следовательно  . Будет ли зависеть результат от выбора системы координат? Воспользуемся выражением для вычисления в цилиндрической системе координат: .Радиус-вектор в этой системе координат  . Следовательно . Очевидно, что такой же результат получим, проведя вычисления в сферической системе координат, где  , а выражение для градиента выглядит так: .2).При вычислении  (а в дальнейшем и ) не следует забывать, что оператор набла -это одновременно и вектор, и дифференциальный оператор. Поэтому следует сначала рассматривать его действие, как действие дифференциального оператора (не забывая о правиле вычисления производной сложной функции  ), а потом рассматривать его как вектор (например, в скалярном или векторном произведениях).Предположим, требуется определить  , если  . Здесь R –модуль радиус-вектора. Тогда необходимо записать: 3).Определим поток радиус-вектора через сферическую поверхность s, центр которой совпадает с началом координат. Эту задача можно решить двумя способами. а). По определению поток Ф =  . В рассматриваемой задаче, благодаря ее сферической симметрии, можно утверждать, что векторы и  сонаправлены, следовательно скалярное произведение векторов, стоящее под знаком интеграла, можно заменить произведением модулей этих векторов. Кроме того, очевидно, что значение модуля радиус-вектора для всех точек поверхности интегрирования одинаково и, следовательно, сомножитель R можно вынести за знак интегрирования. б). Поток вектора через поверхность связан с интегралом по объему, заключенному в рассматриваемую поверхность, от дивергенции этого вектора теоремой Остроградского – Гаусса. Следовательно второй способ решения указанной задачи:  .4). Предположим, что требуется определить поток радиус-вектора сквозь поверхность цилиндра радиуса a и высоты z = h. В этом случае решение по способу а) предыдущей задачи затруднительно, т.к. требует вычисления скалярного произведения  для точек, принадлежащих торцам и боковой поверхности цилиндра. Поэтому удобно поток вычислить, как  .Ротор (вихрь) векторного поля. Можно говорить о вихревом источнике, который связан с циркуляцией векторного поля вокруг него. Циркуляция векторного поля по замкнутому конуру С определяется как скалярный линейный интеграл  .  – векторный дифференциал длины, направление вектора совпадает в точках контура с направлением касательной к контуру интегрирования. Для определения в некоторой точке функции, которая является мерой силы вихревого источника, контур необходимо сделать малым и ориентировать его так, чтобы циркуляция была максимальной.Определяют   – векторная функция точки. Если ротор векторного поля равен 0, то такое поле называют безвихревым (консервативным).Если выражение для ротора проинтегрировать по поверхности, опирающейся на замкнутый контур С, получим соотношение, которое называют теоремой Стокса:  Если поверхностный интеграл вычислять по замкнутой поверхности (контур отсутствует), то 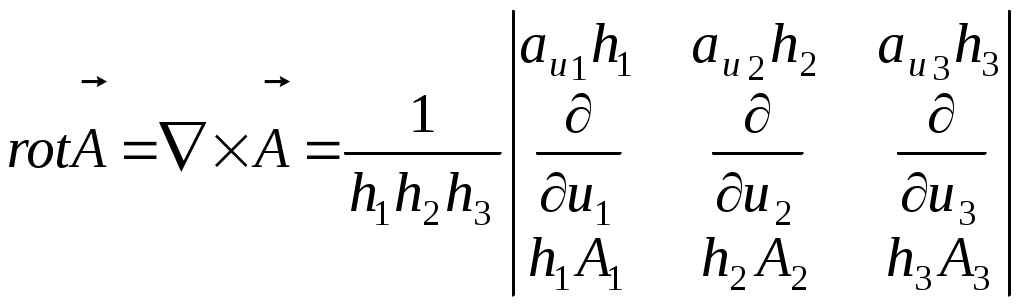  .В декартовой системе координат 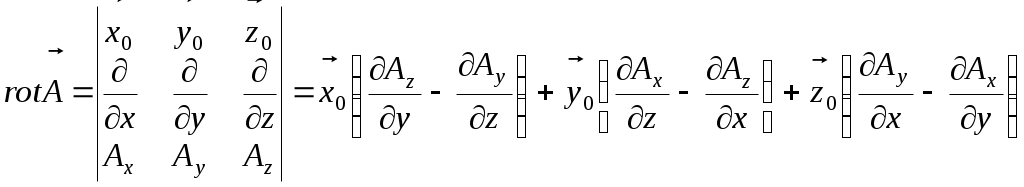 .1).Рассмотрим пример вычисления ротора функции, являющейся произведением вектора и скалярной функции координат. Итак, требуется определить  , где - радиус-вектор, а R– модуль этого вектора. . Здесь учтено замечание, сделанное при вычислении дивергенции сложной функции. Нетрудно убедиться, что второе слагаемое в рассматриваемой задаче равно 0, так как  . Вычислим градиент, входящий в первое слагаемое.   .Продолжим вычисление  .Рассмотрены дифференциальные операции первого порядка со скалярными и векторными полями. Дифференциальные операции второго порядка: 1.  . Следовательно, если векторное поле – безвихревое, то его можно выразить как градиент скалярного поля. Если  = 0, то можно определить скалярное поле , как = - .2.  0. Следовательно, если дивергенция векторного поля равна 0, то поле можно представить как ротор другого векторного поля. Если  = 0, то можно определить векторное поле , такое, что  .3.  . - это оператор Лапласа. Он может быть применен как к векторной, так и к скалярной величине. В декартовой системе координат  .4.  |