|
|
Решение электродинамика. Бабенко примеры задач. Электродинамика и распространение радиоволн упражнения и задачи
Определим напряженность электрического поля  = - grad = - grad
В сферической системе координат
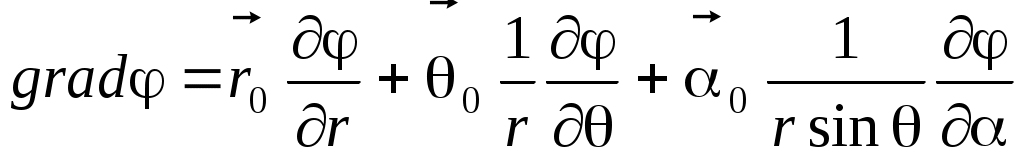 . Благодаря осевой симметрии . Благодаря осевой симметрии 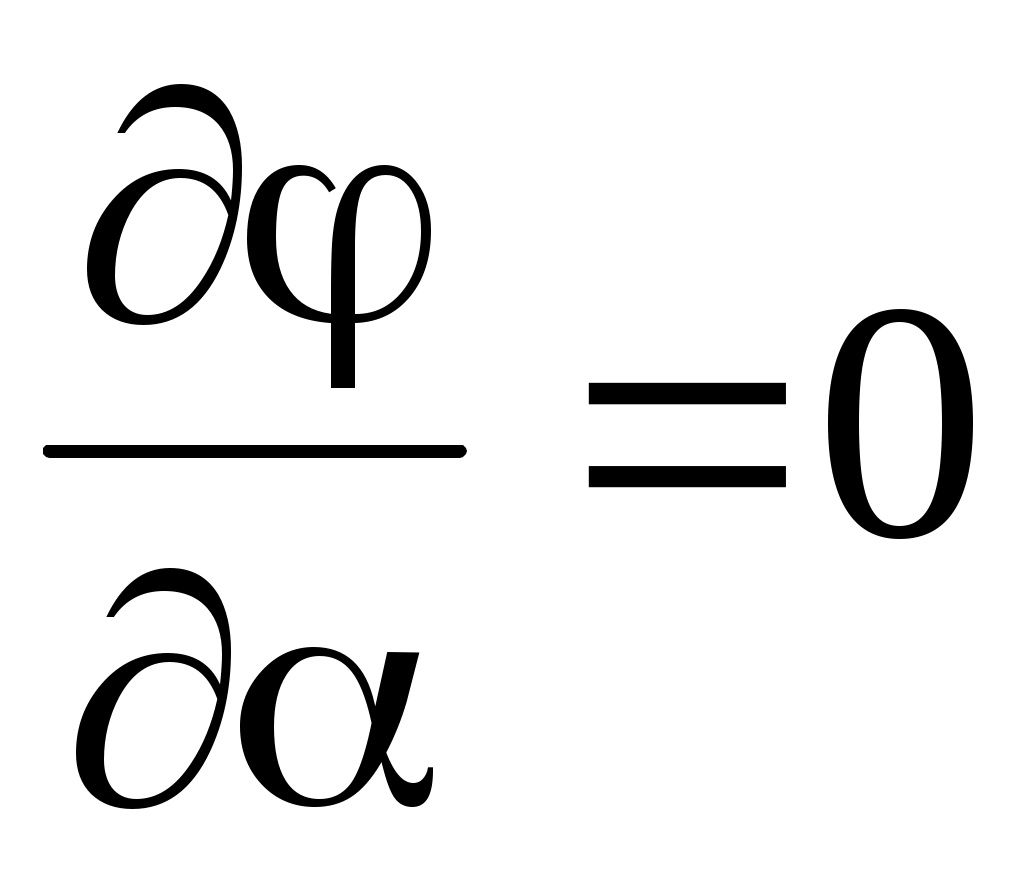 . .
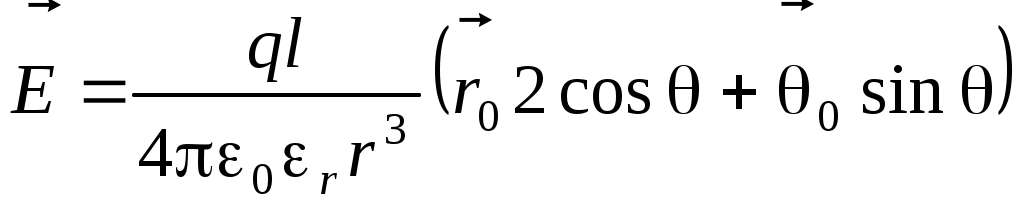 - вектор - вектор  не зависит от угла α (поле обладает осевой симметрией) и имеет две составляющие. Картина силовых линий поля диполя не зависит от угла α (поле обладает осевой симметрией) и имеет две составляющие. Картина силовых линий поля диполя

4. Поле точечного заряда, расположенного над идеально проводящей плоскостью. Рассмотрим влияние точечного заряда на проводящую плоскость. В результате электростатической индукции на границе должен появиться некий заряд, создающий дополнительное поле, которое, налагаясь на первоначальное поле источника, приведет к удовлетворению граничных условий. Задача определения поля точечного заряда, расположенного над проводящей плоскостью, эквивалентна задаче определения поля двух зарядов: заданного q и некоторого фиктивного заряда (-q), являющегося зеркальным изображением первого, находящихся в неограниченном диэлектрике.
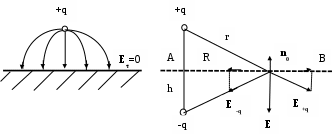
Поле в верхнем полупространстве удовлетворяет граничному условию Е = 0, граница раздела – эквипотенциальная поверхность. Плоскость АВ, расположенная симметрично относительно зарядов, - эквипотенциальная поверхность с нулевым потенциалом, в точках этой плоскости вектор  ориентирован в направлении ( ориентирован в направлении (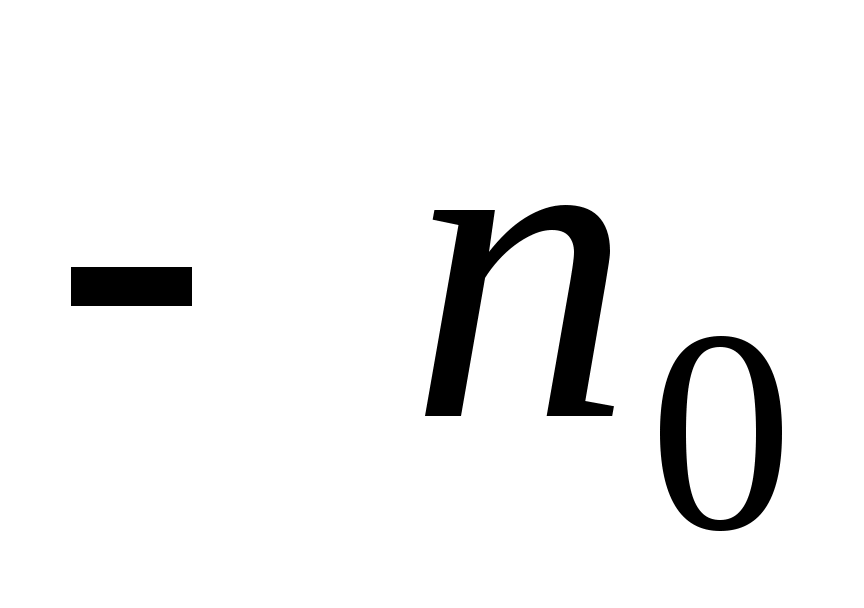 ). Полный заряд, наведенный на плоскости АВ, ). Полный заряд, наведенный на плоскости АВ,
q'=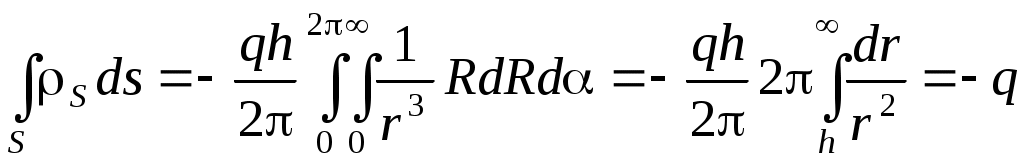 , , 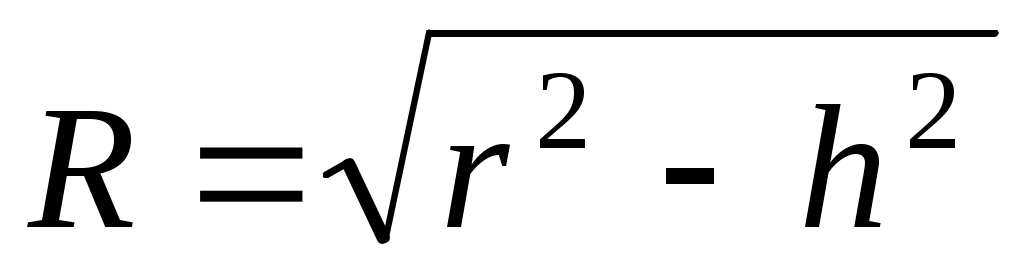 , ,
плотность поверхностного заряда s=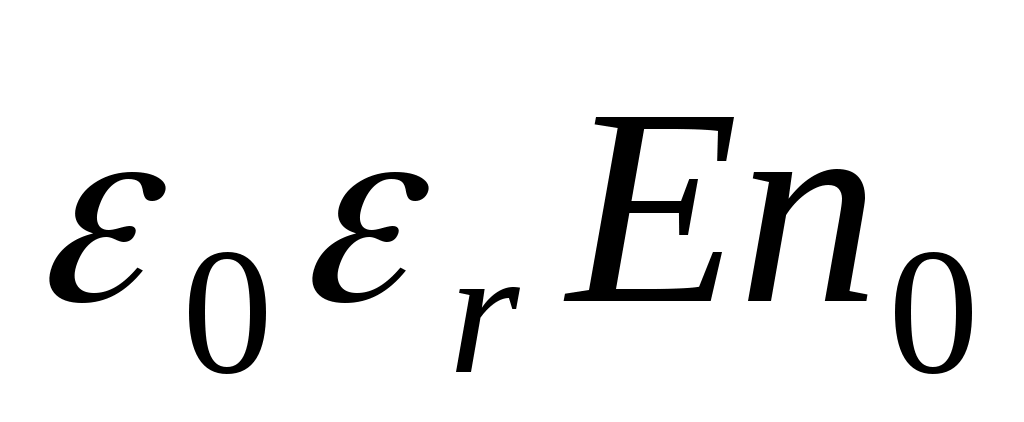 , где вектор напряженности электрического поля определяется как результат сложения полей двух точечных зарядов, т.е. совпадает со значением вектора , где вектор напряженности электрического поля определяется как результат сложения полей двух точечных зарядов, т.е. совпадает со значением вектора  поля электрического диполя при = /2. поля электрического диполя при = /2. 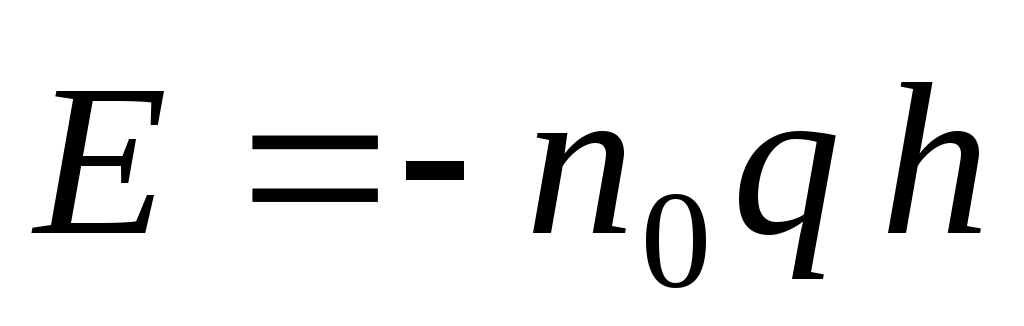 (2 0rr3). (2 0rr3).
Введение фиктивного сосредоточенного заряда эквивалентно учету всех зарядов, наведенных на границе раздела. Метод замены проводящей поверхности фиктивным сосредоточенным зарядом получил название метода зеркального изображения. В силу принципа суперпозиции метод
зеркального изображения можно обобщить на случай произвольной системы зарядов, расположенных над проводящей плоскостью.
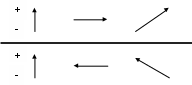
Стационарное магнитное поле.
Система уравнений стационарного электромагнитного поля (поле неизменно во времени, 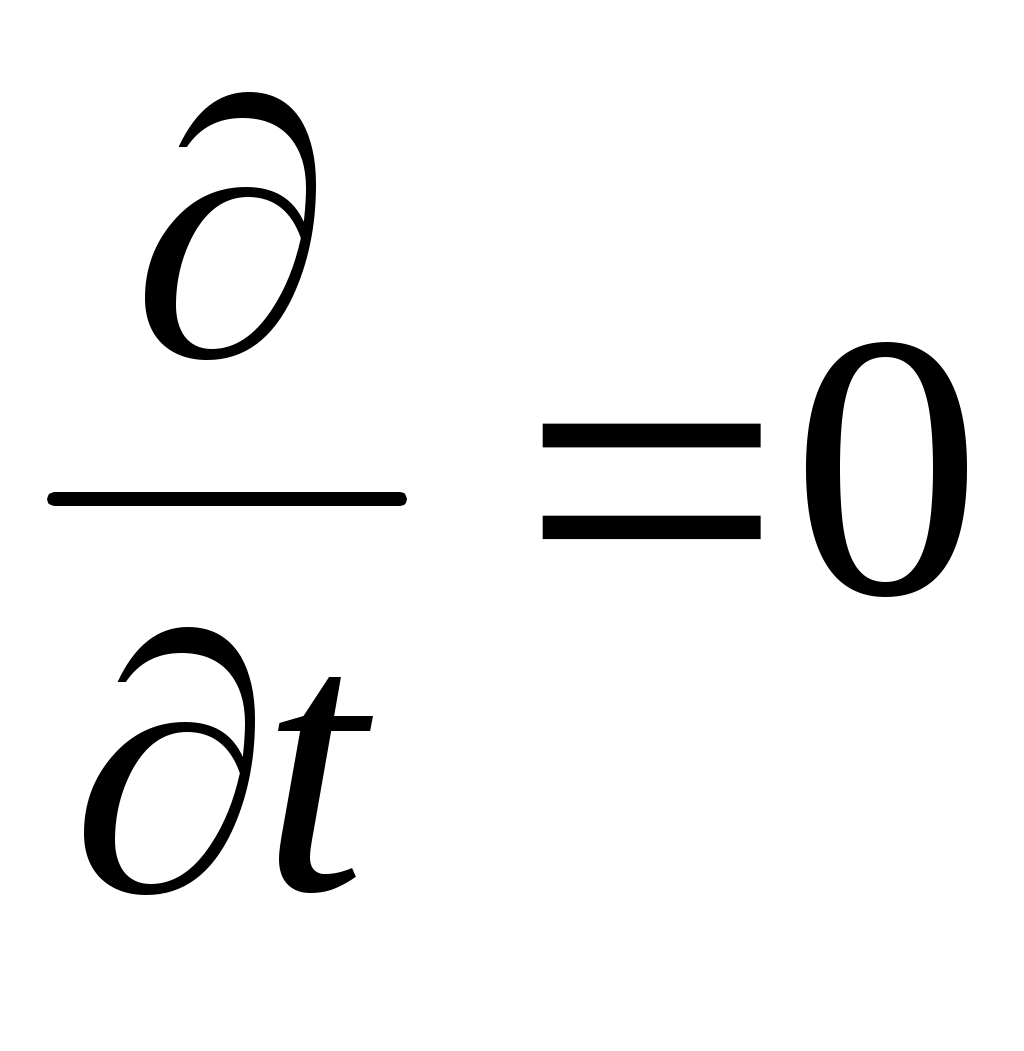 ) ) 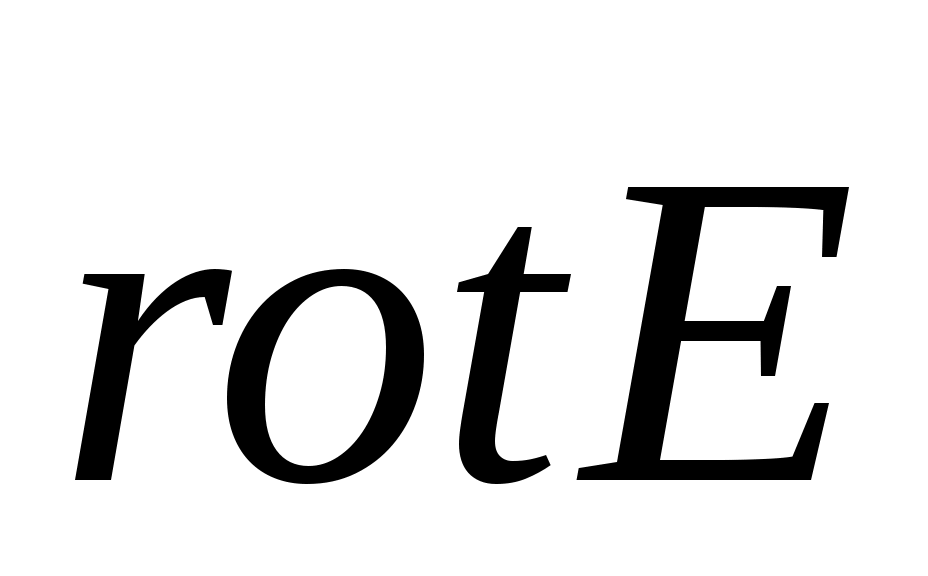 = 0 = 0 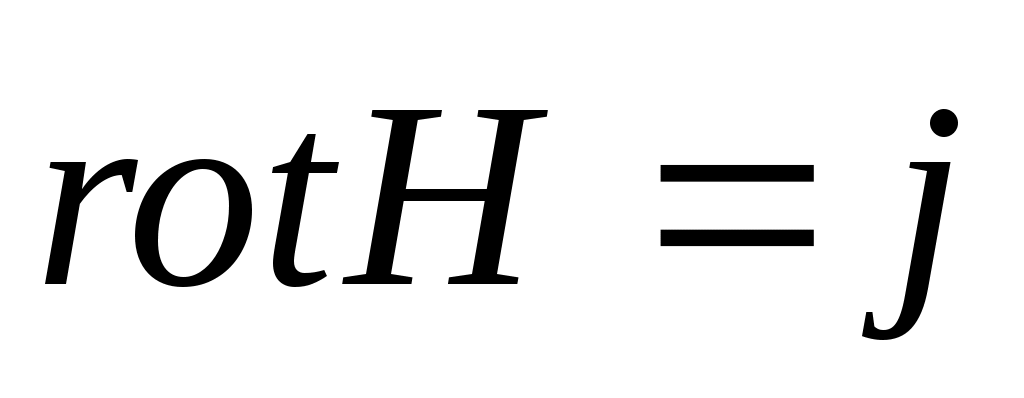
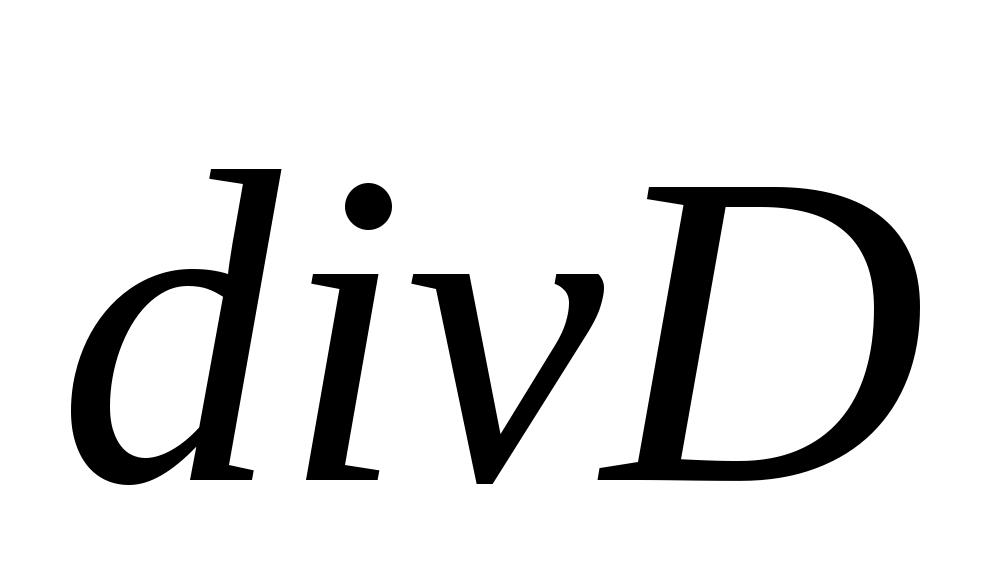 = = 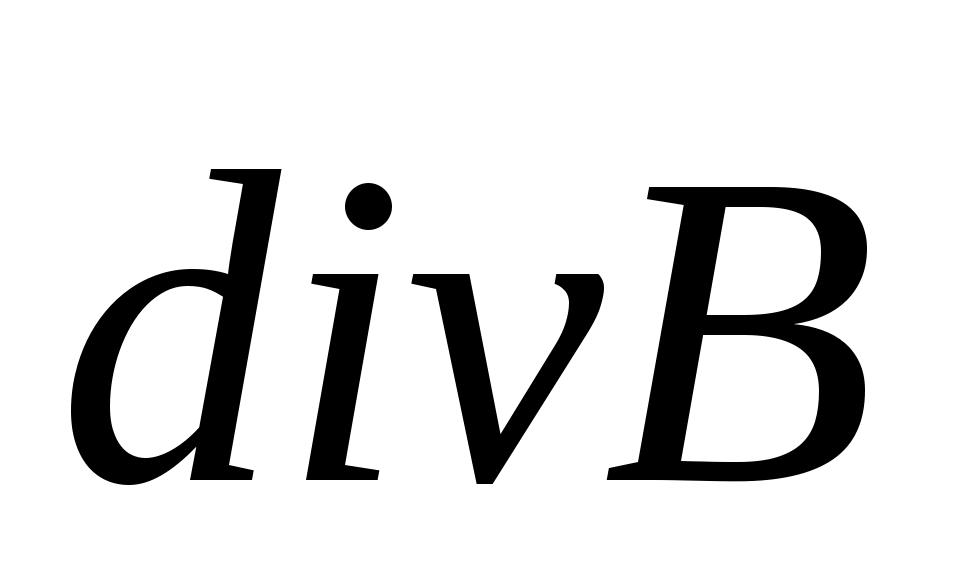 = 0 = 0
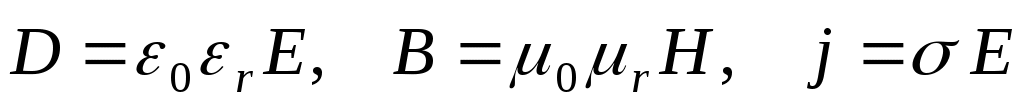
При наличии тока (j 0) все уравнения взаимно связаны. Если плотность тока – заданная величина, магнитное поле может быть определено независимо от электрического при решении системы уравнений:
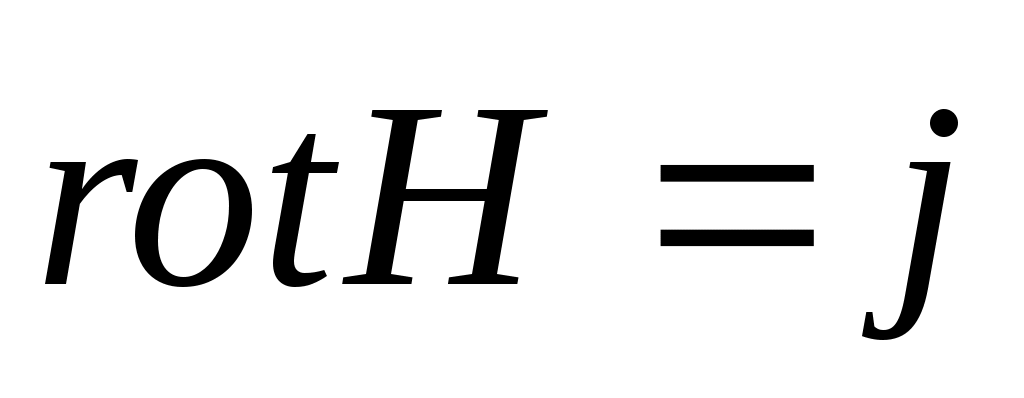 - магнитное поле соленоидальное (ротор поля не равен 0), - магнитное поле соленоидальное (ротор поля не равен 0), 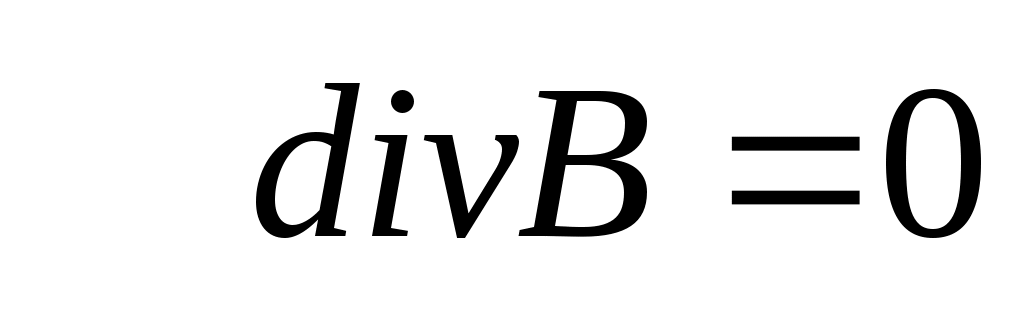 - линии магнитного поля не имеют начала и конца (в природе не существует магнитного аналога , т.е. не существует магнитных зарядов). - линии магнитного поля не имеют начала и конца (в природе не существует магнитного аналога , т.е. не существует магнитных зарядов).
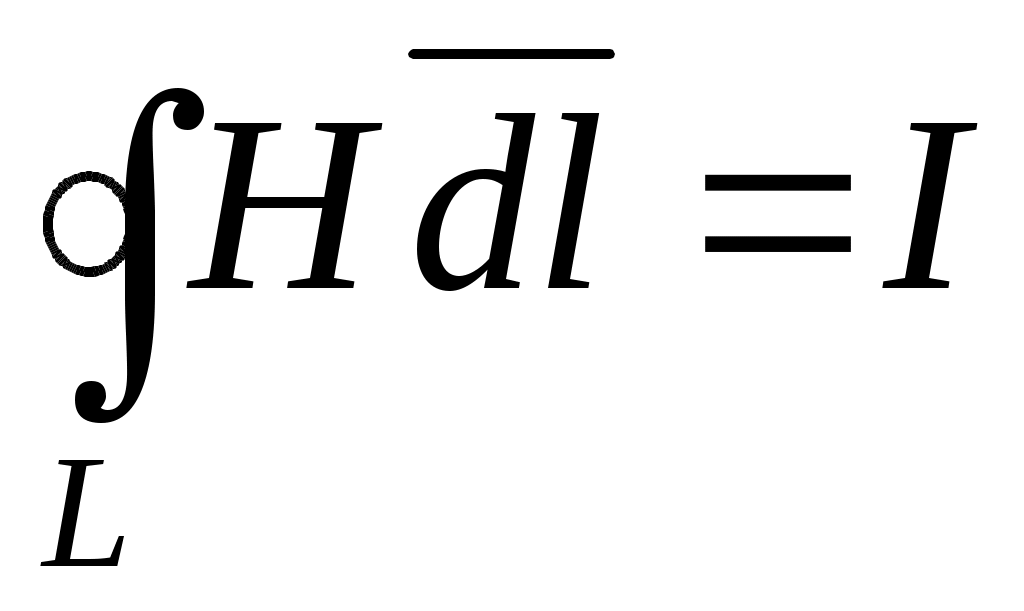 - в правой части равенства стоит алгебраическая сумма токов, которые охватывает контур L, - в правой части равенства стоит алгебраическая сумма токов, которые охватывает контур L,
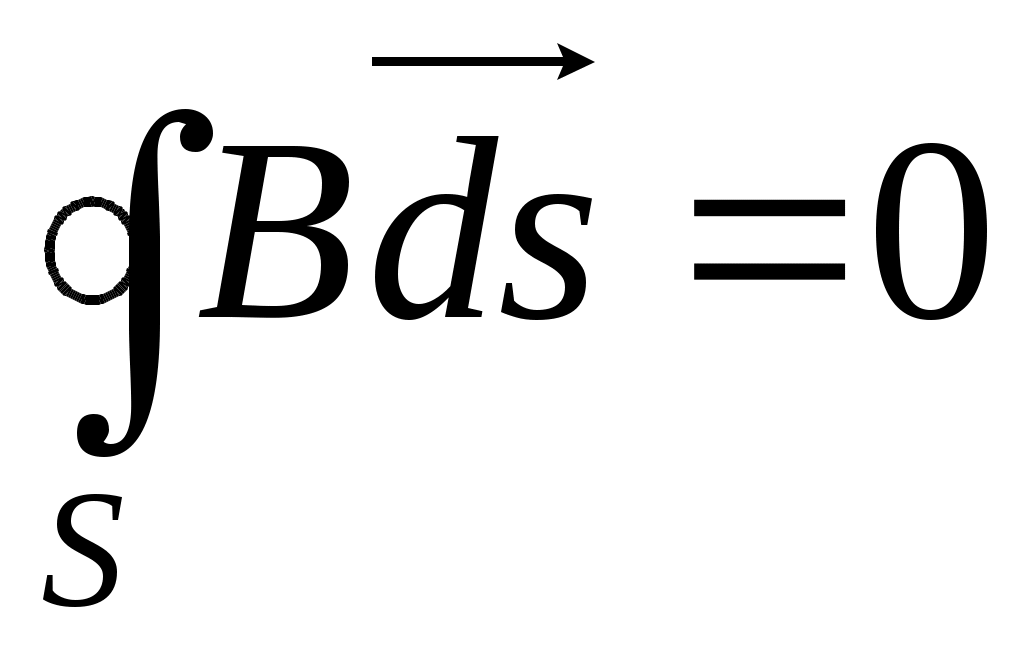 - поток вектора - поток вектора 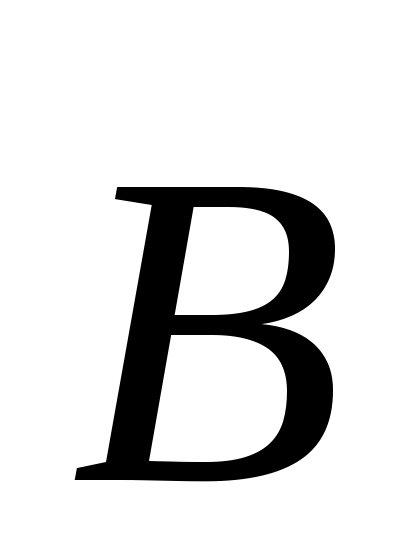 сквозь замкнутую поверхность равен 0. сквозь замкнутую поверхность равен 0. 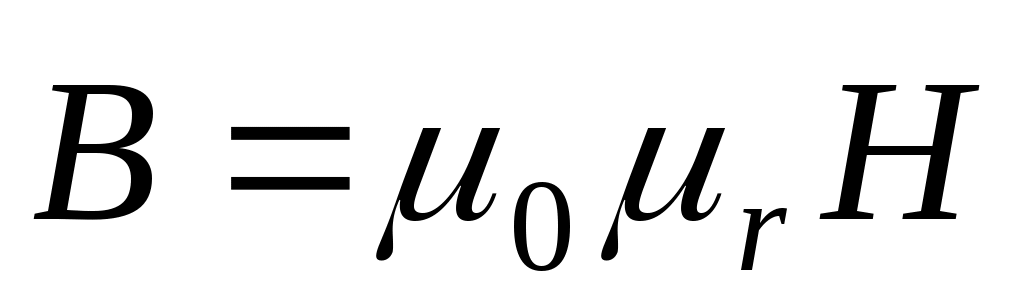
Это система уравнений стационарного магнитного поля. Для однородной среды (r = const) решение этой системы имеет вид
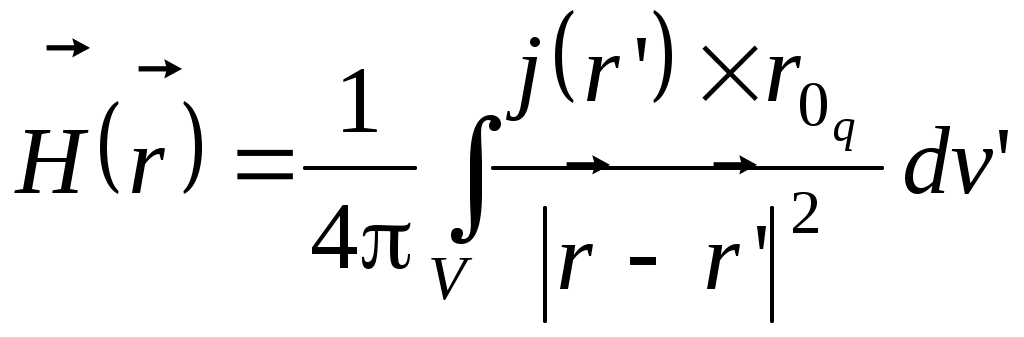
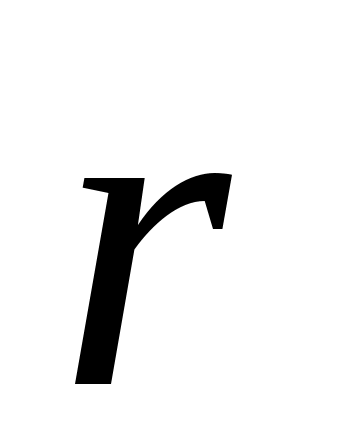 – радиус – вектор точки наблюдения, – радиус – вектор точки наблюдения, 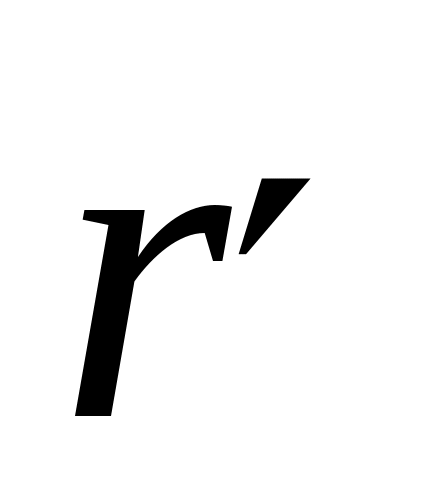 – радиус – вектор точки интегрирования в среде, где течет ток j. Это – обобщенный закон Био-Савара. – радиус – вектор точки интегрирования в среде, где течет ток j. Это – обобщенный закон Био-Савара.
Для линейного тока I, проходящего по контуру L, магнитное поле описывается обычным законом Био-Савара
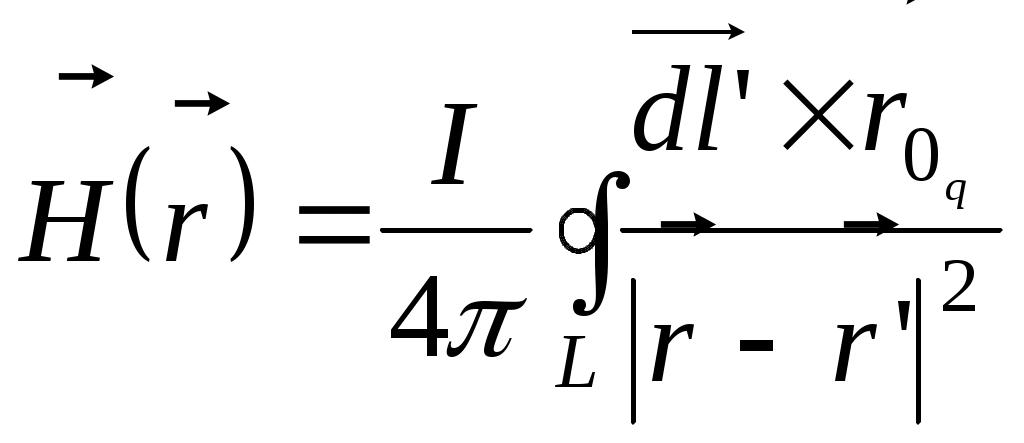
(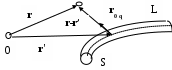 Линейным считается ток нитевидного Линейным считается ток нитевидного
проводника, если расстояния 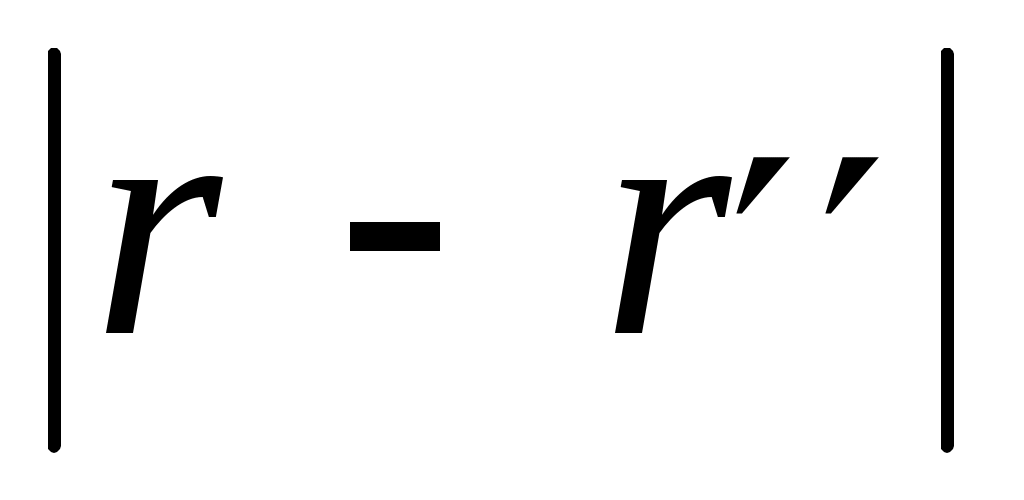
остаются в процессе интегрирования
значительно больше поперечного размера проводника).
Закон Био-Савара записывают и в форме дифференциала
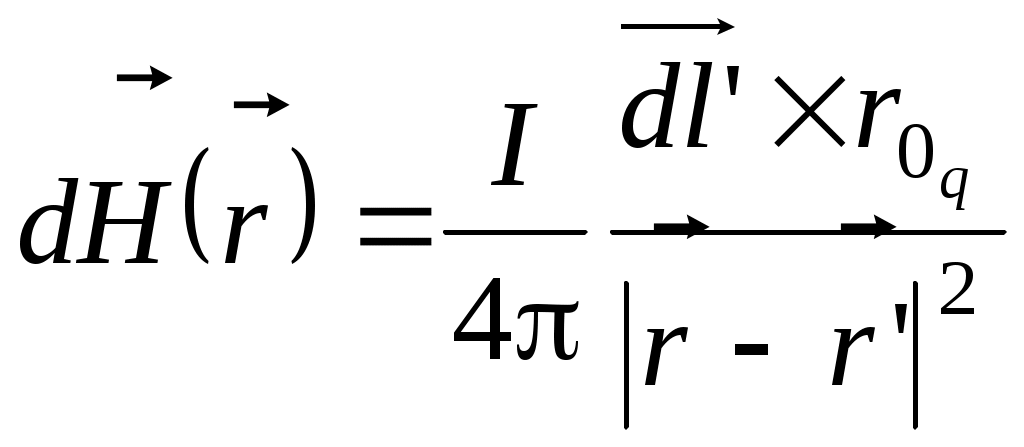
При этом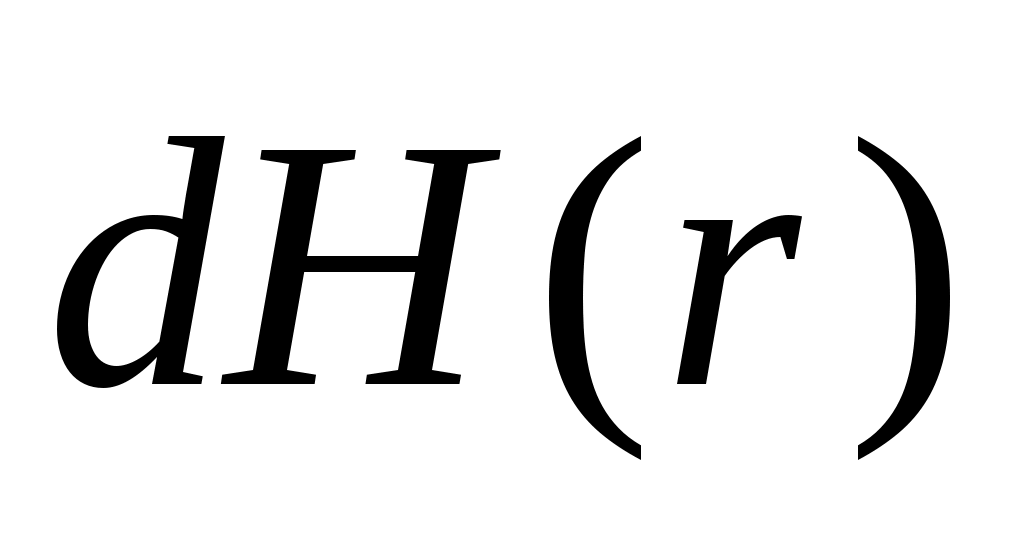 – вклад в полное магнитное поле – вклад в полное магнитное поле 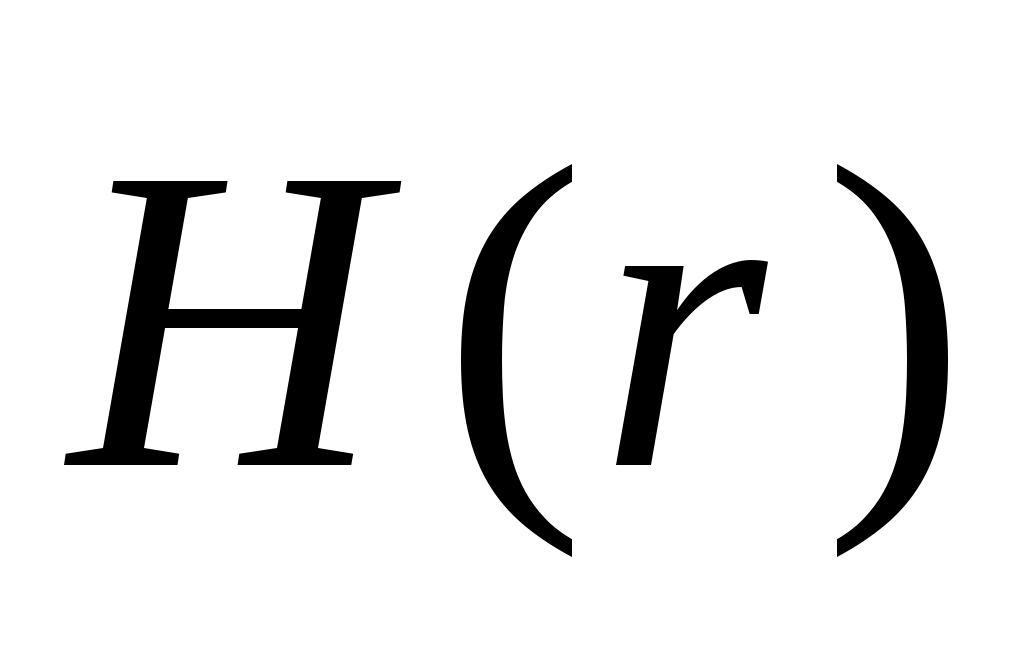 , создаваемый элементом контура , создаваемый элементом контура 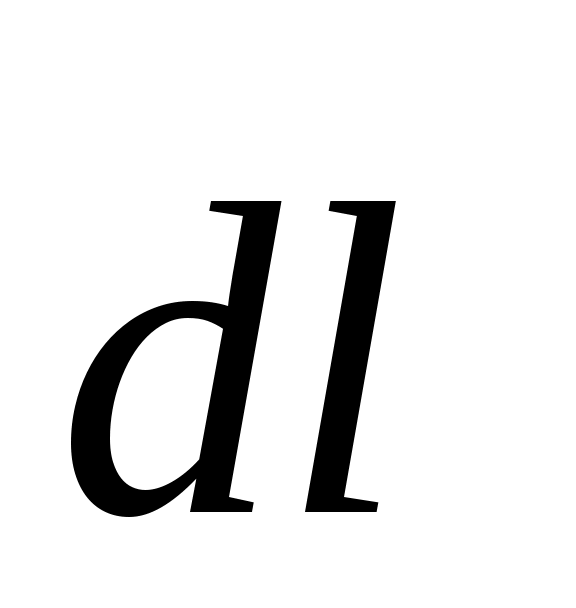 с током I. с током I.
Закон Био-Савара дает полное решение системы уравнений для заданного распределения тока в однородной среде. Но также используют и вспомогательные функции – потенциалы.
Вводят вспомогательную величину – векторный потенциал . По определению . По определению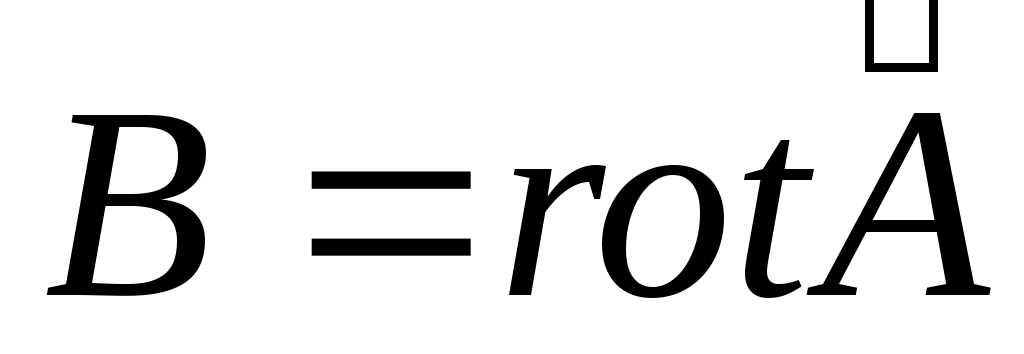 . Для векторного потенциала справедливо уравнение Пуассона . Для векторного потенциала справедливо уравнение Пуассона 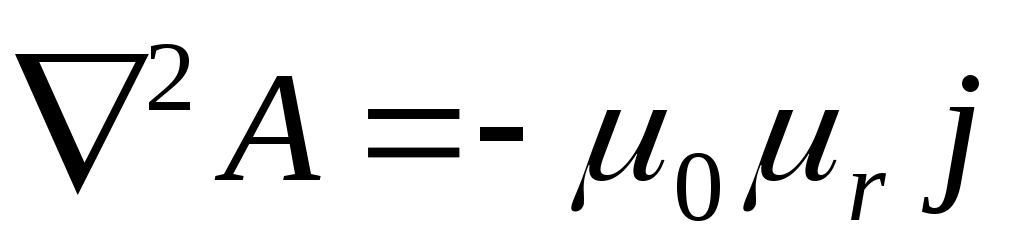 . Его решение . Его решение 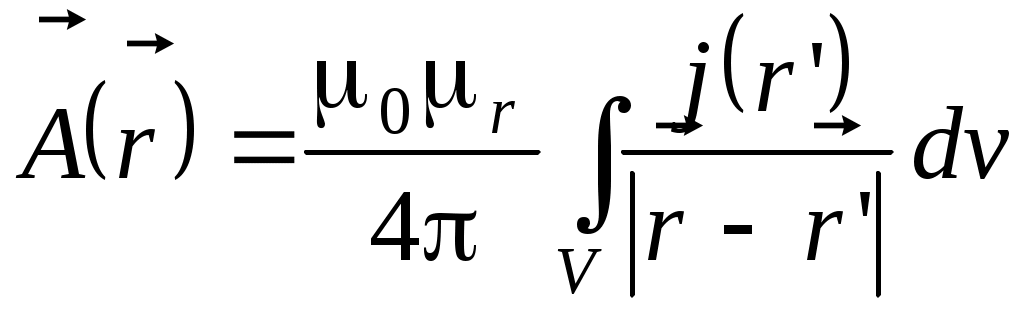 . .
Для линейных токов 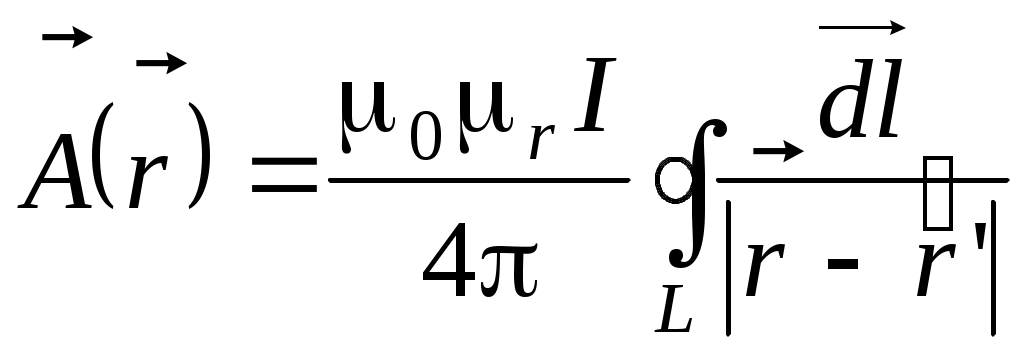
После нахождения 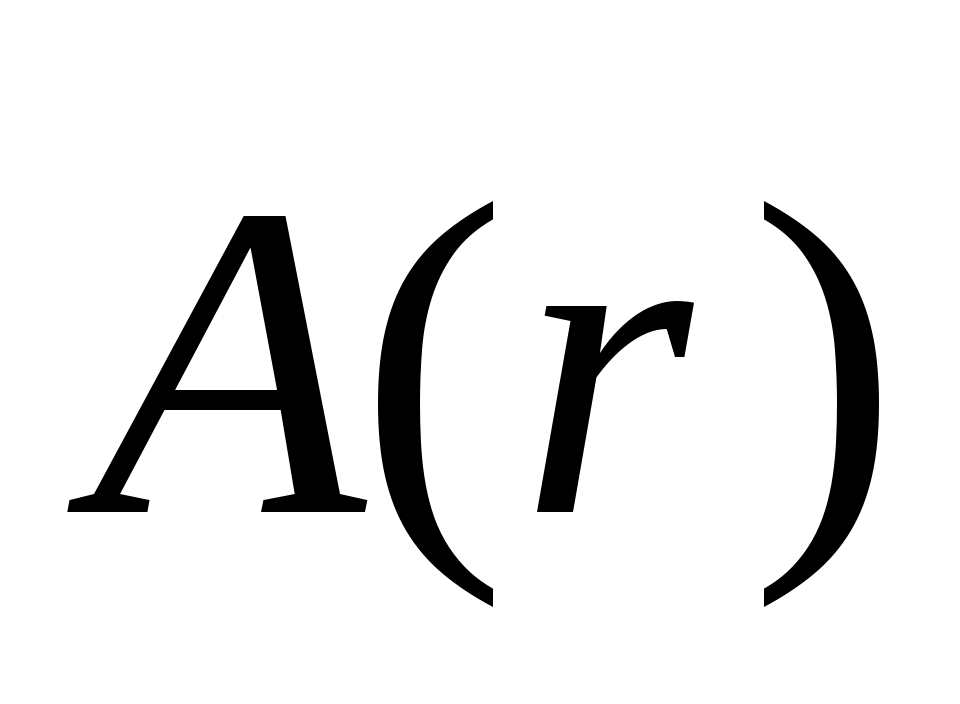 магнитное поле определяется как магнитное поле определяется как  0 r. 0 r.
В ряде случаев такой путь оказывается менее трудоемким.
Рассмотрим несколько примеров.
1). Определить напряженность магнитного поля внутри и вне бесконечно длинного прямого провода радиуса b, по которому течет ток I.
Задача имеет цилиндрическую симметрию: предложенная к рассмотрению система бесконечна вдоль оси z и нет зависимости от угла φ. Следовательно, для решения задачи можно использовать теорему о циркуляции  , выбирая, в качестве конура интегрирования, окружность r = const, расположенную внутри или вне проводника при произвольном z. , выбирая, в качестве конура интегрирования, окружность r = const, расположенную внутри или вне проводника при произвольном z.
Известно, что силовые линии магнитного поля линейного тока – окружности. Направление вектора  , касательного к окружности, связано с направлением тока правилом правой руки. Если направление тока в проводнике совпадает с направлением оси z, то искомый вектор , касательного к окружности, связано с направлением тока правилом правой руки. Если направление тока в проводнике совпадает с направлением оси z, то искомый вектор 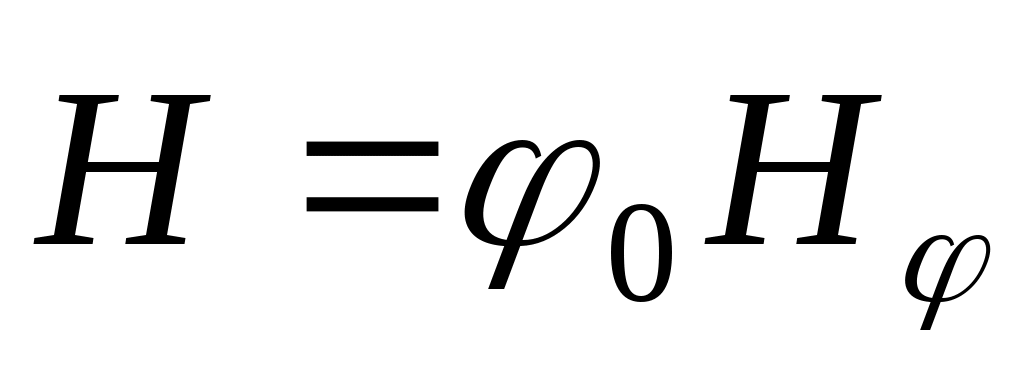 . Векторный дифференциал длины направлен по касательной к рассматриваемому конуру . Векторный дифференциал длины направлен по касательной к рассматриваемому конуру 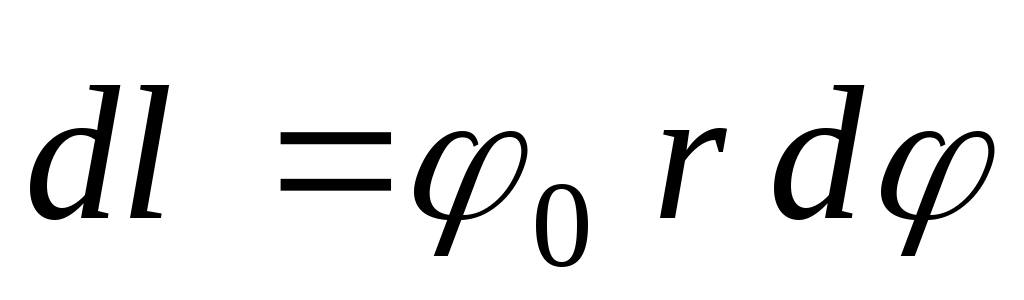 . .
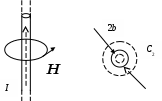
а). Определяя напряженность поля внутри проводника, выберем в качестве конура интегрирования окружность С1, радиус которой r1 меньше b.
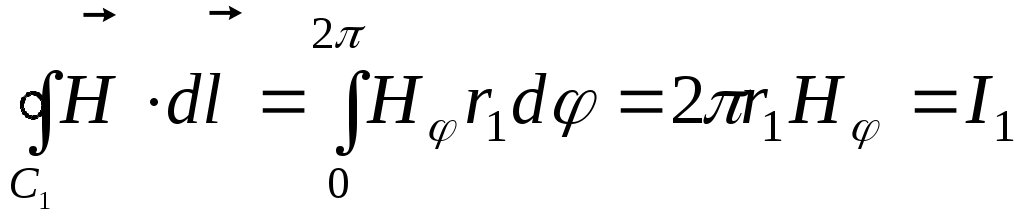 . Здесь I1 – ток, протекающий через площадку, ограниченную контуром С1. . Здесь I1 – ток, протекающий через площадку, ограниченную контуром С1. 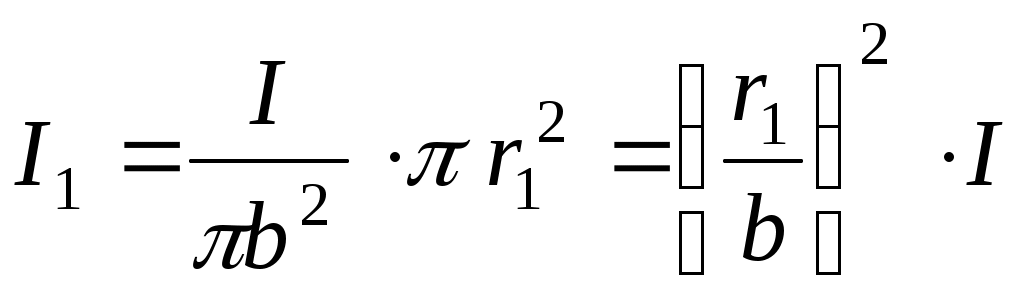 . .
Следовательно, внутри проводника (при r1< b) напряженность поля
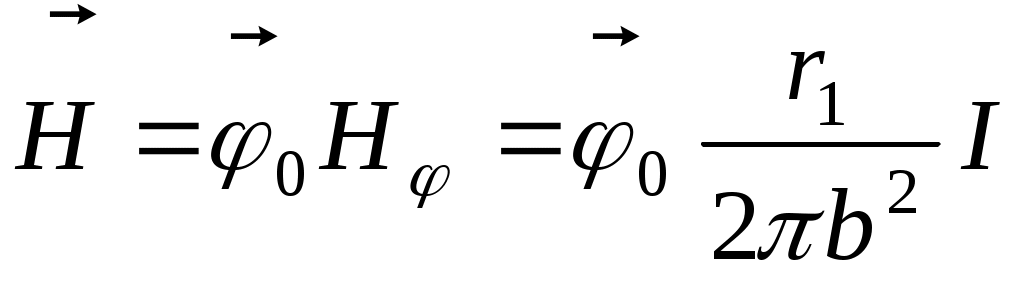 . .
б). При определении напряженности магнитного поля вне проводника радиус контура интегрирования полагаем r2 > b. При этом контур интегрирования будет охватывать весь ток I. 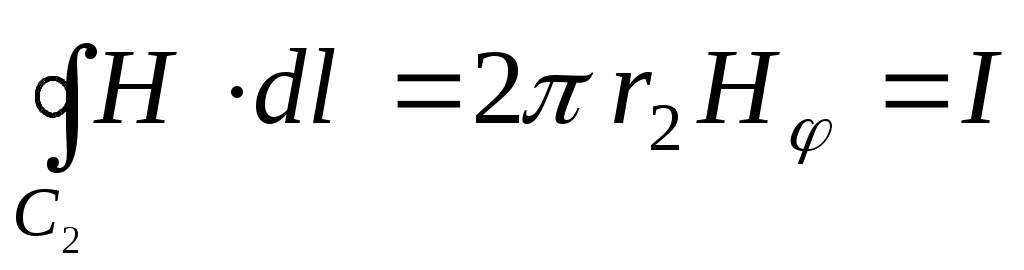 . .
Напряженность поля вне проводника (r2 > b) 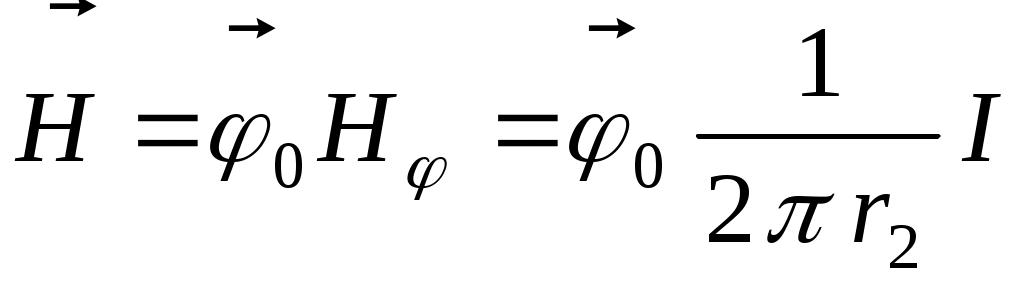 . .
2). По замкнутому проводнику протекает постоянный ток I. Определить вектор магнитной индукции, которую создает прямолинейный участок проводника длиной 2L в точке Р. Указанная точка расположена симметрично относительно концов участка на расстоянии rот его центра.
Предложенную задачу решим двумя способами.
а). Вспомним выражение для векторного потенциала для линейного тока
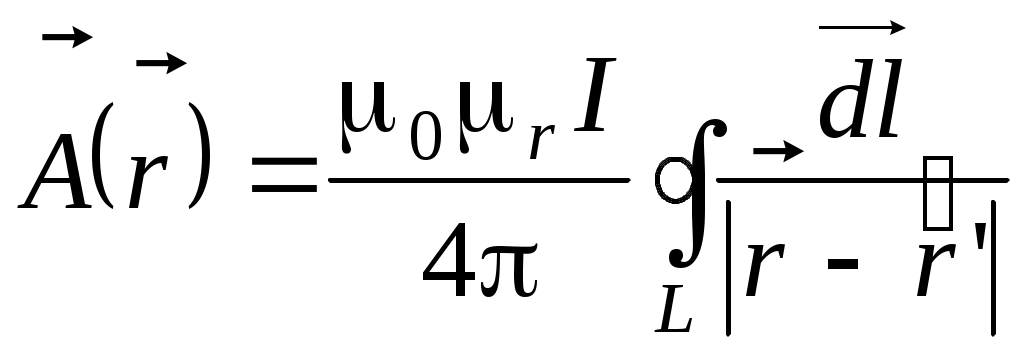 .Предположим, что прямолинейный участок проводника ориентирован по оси z: .Предположим, что прямолинейный участок проводника ориентирован по оси z: 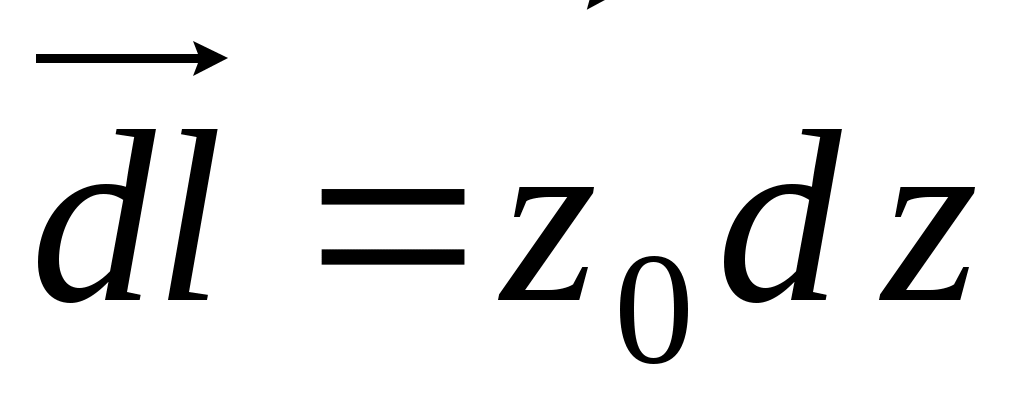 . Расстояние от точки интегрирования до . Расстояние от точки интегрирования до
точки Р: 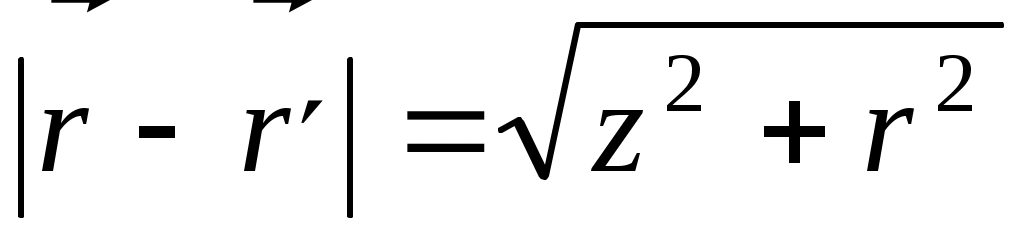 . Следовательно, векторный потенциал в точке Р . Следовательно, векторный потенциал в точке Р 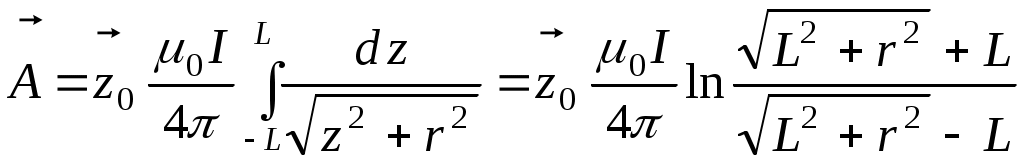 . .
Далее определяем вектор магнитной индукции
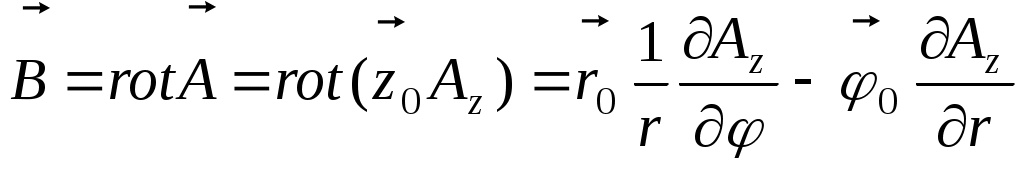 . .
Цилиндрическая симметрия предполагает, что 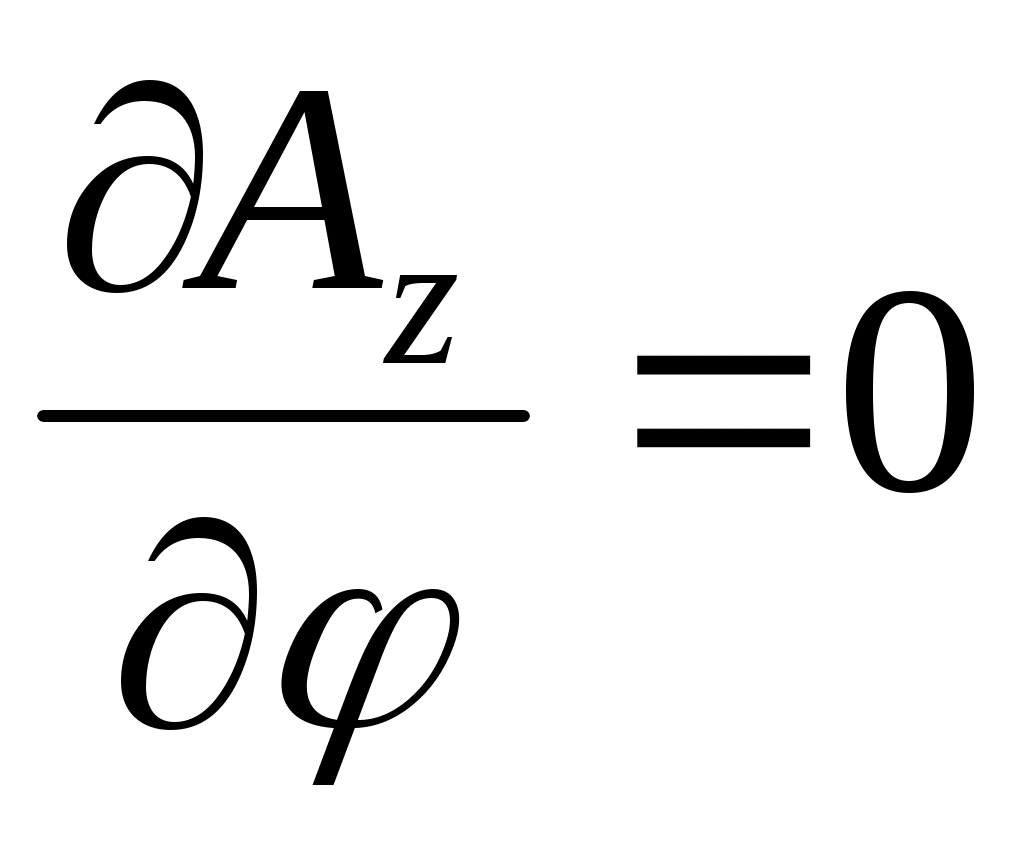 . Следовательно . Следовательно
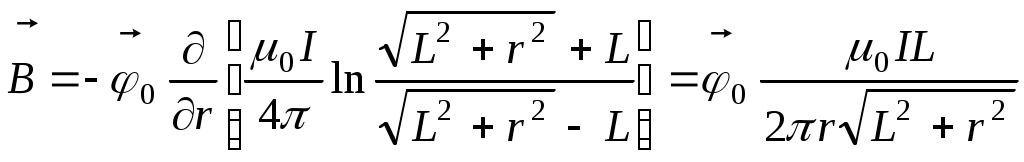 . .
Если r<< L, то 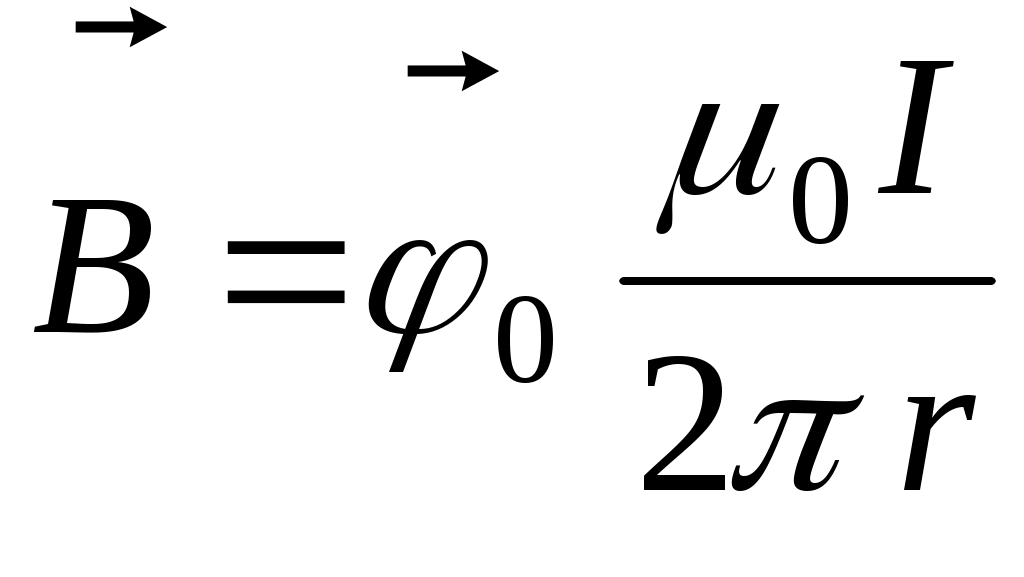 , что соответствует результату, полученному при решении задачи 1. , что соответствует результату, полученному при решении задачи 1.
б). Воспользуемся дифференциальной формой закона Био-Савара:
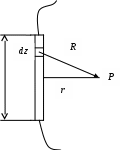 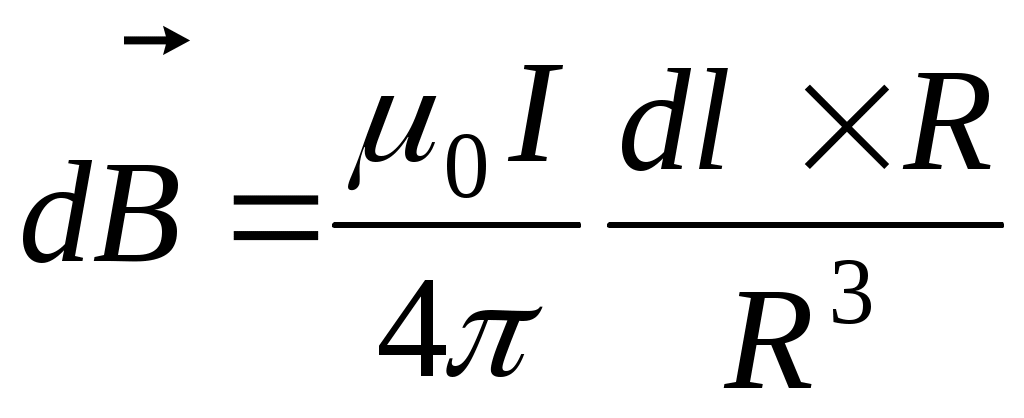

В нашей задаче вектор, соединяющий элемент dz
участка проводника и точку Р, 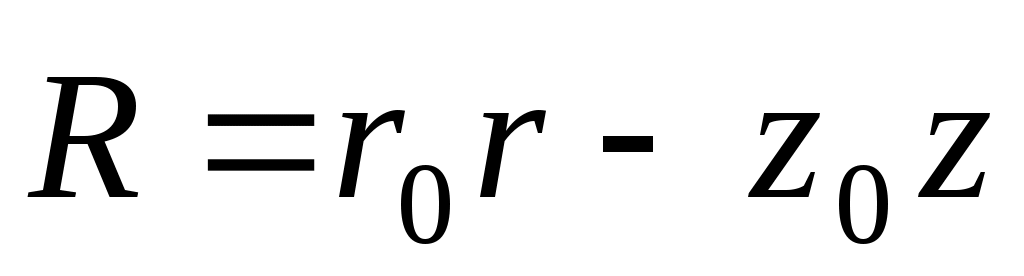 . .
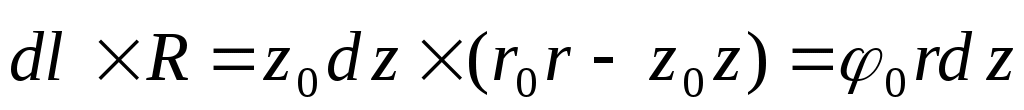 . .
Следовательно
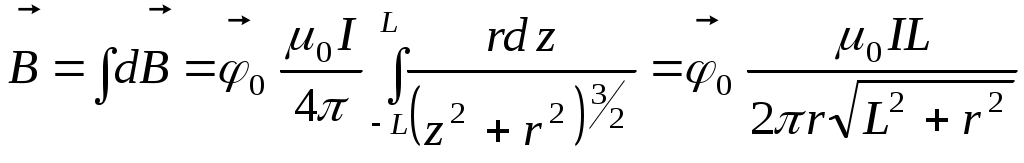
Плоские электромагнитные волны.
В отсутствии сторонних источников любая декартова компонента векторов 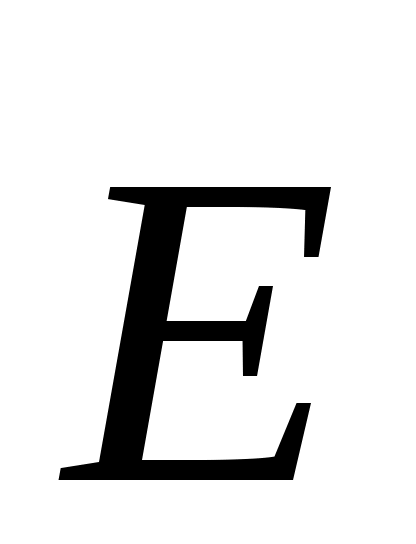 и и  удовлетворяет однородному волновому уравнению удовлетворяет однородному волновому уравнению
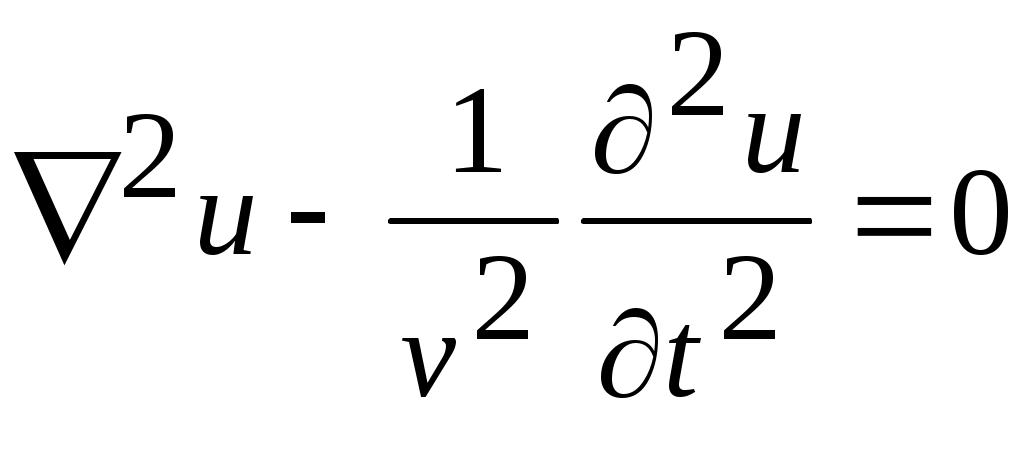 . .
Решение уравнения, зависящее только от одной координаты z и времени t представляет собой наложение двух возмущений, каждое из которых распространяется вдоль z в сторону возрастания или убывания z со скоростью v 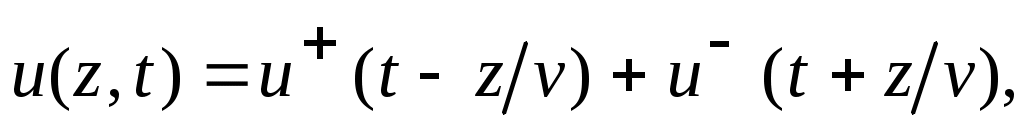
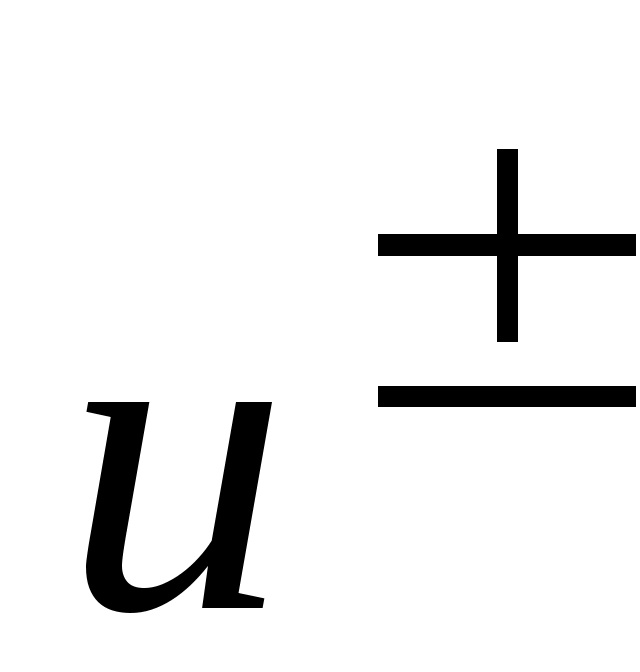 - произвольные дважды дифференцируемые функции. - произвольные дважды дифференцируемые функции.
Для гармонической (монохроматической) волны, распространяющейся в направлении оси z можно записать
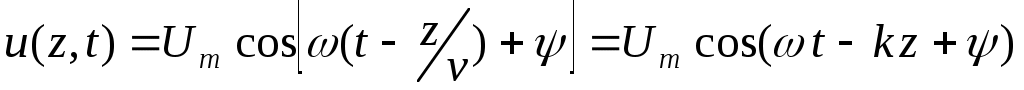 .Здесь .Здесь 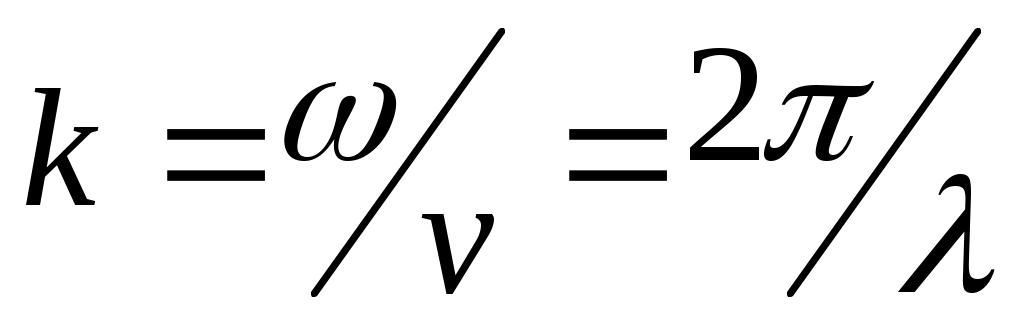 - волновое число. - длина волы – приращение координаты z, при котором фаза меняется на 2. v – скорость распространения волны. - волновое число. - длина волы – приращение координаты z, при котором фаза меняется на 2. v – скорость распространения волны.
Анализ гармонических процессов упрощается при использовании метода комплексных амплитуд.
При замене векторов поля комплексными представлениями:
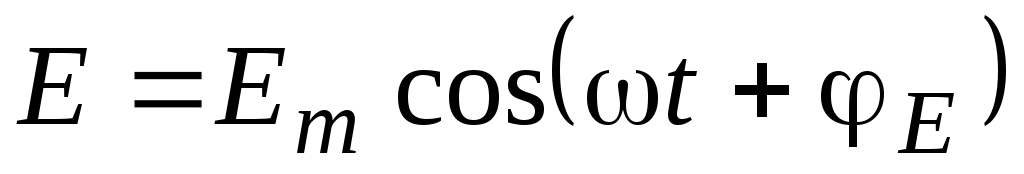 ; ;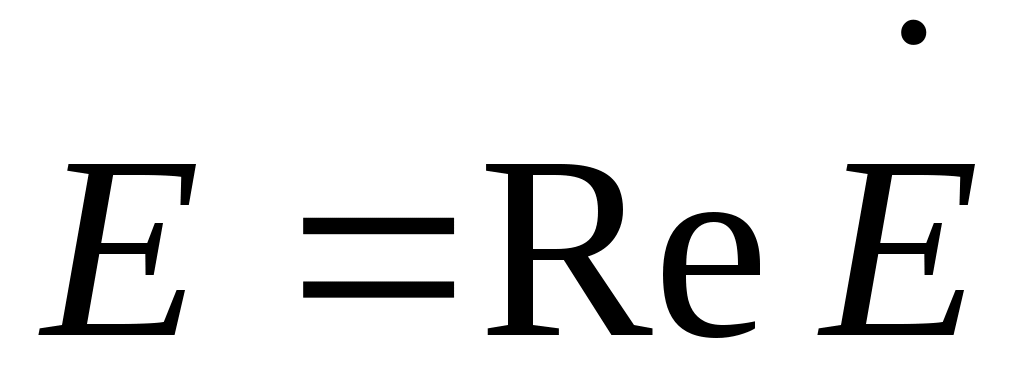 ; ;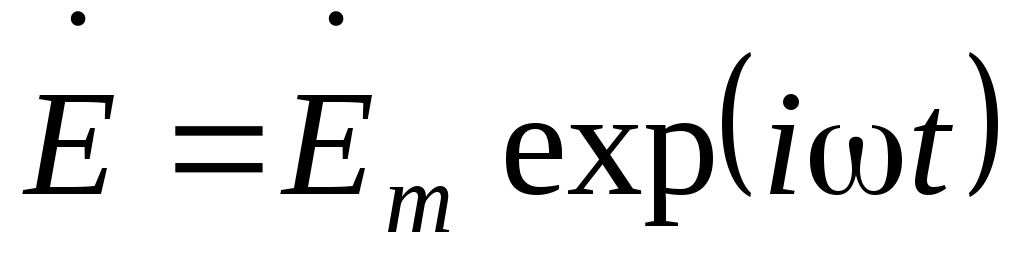 . . 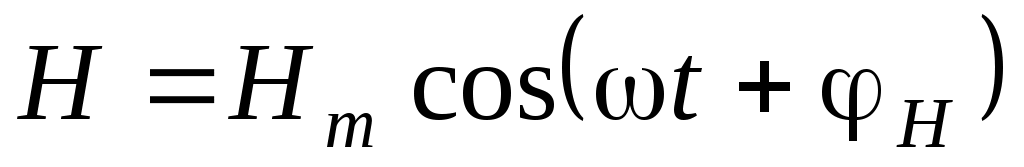 ; ; 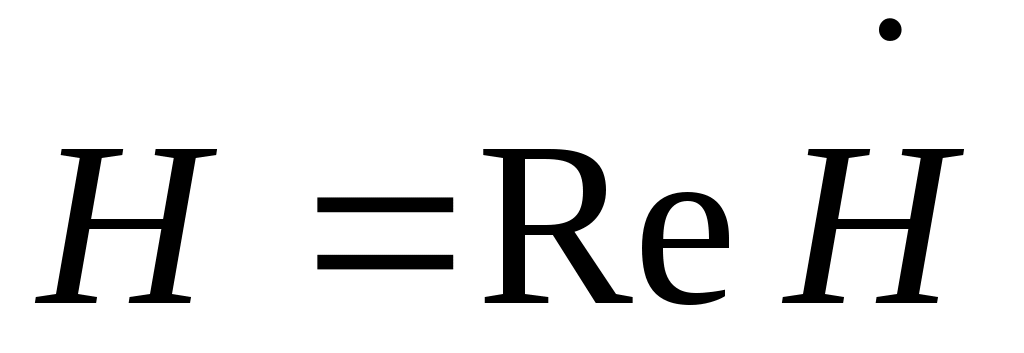 ; ; 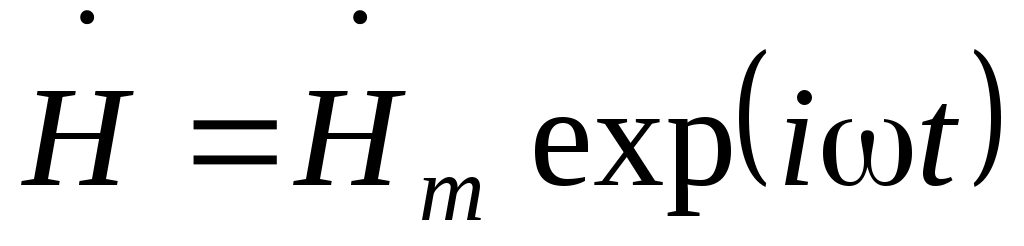 , ,
однородные уравнения для комплексных амплитуд векторов  и и выглядят следующим образом выглядят следующим образом
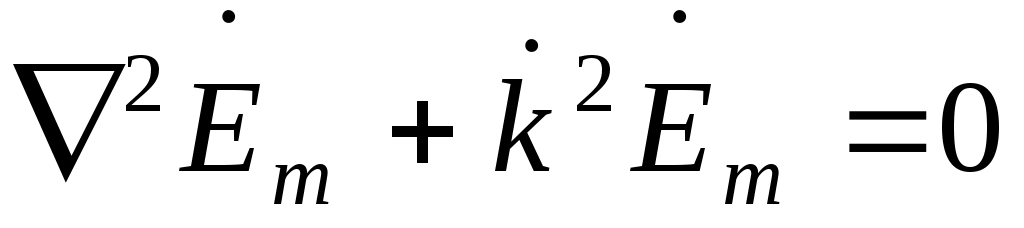 ; ; 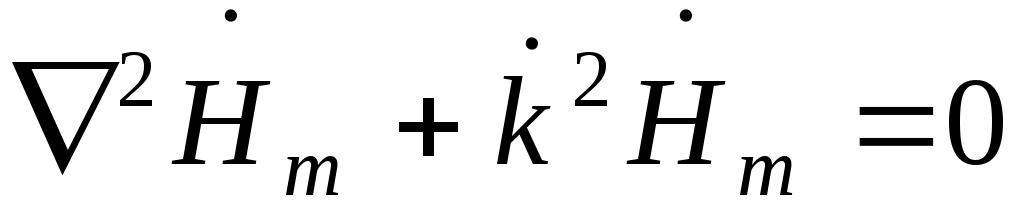 . .
Скорость распространения волны для электромагнитного процесса
v = c / Re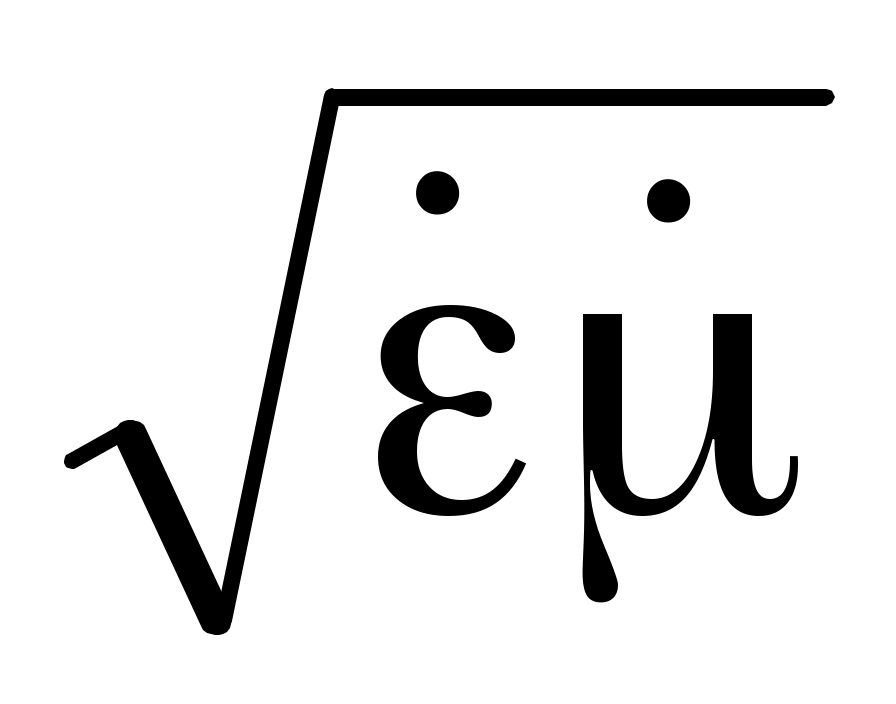 ; v = 1 / ; v = 1 /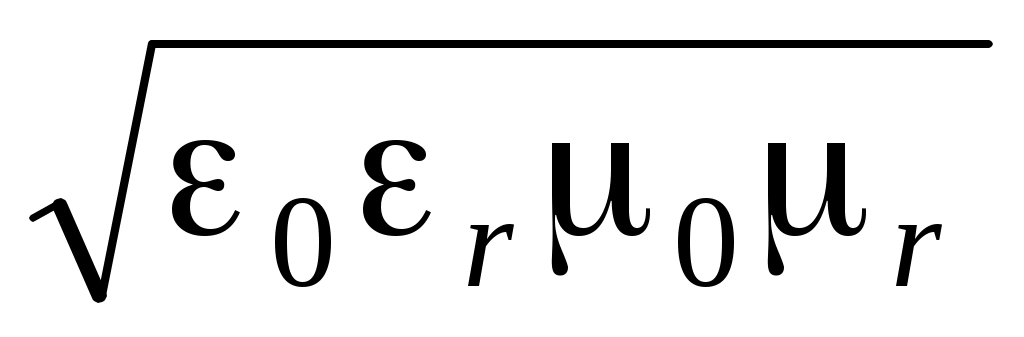 - скорость распространения плоских однородных электромагнитных волн в идеальном диэлектрике. В вакууме - скорость распространения плоских однородных электромагнитных волн в идеальном диэлектрике. В вакууме
(r= 1, r = 1) v = c= 1 / 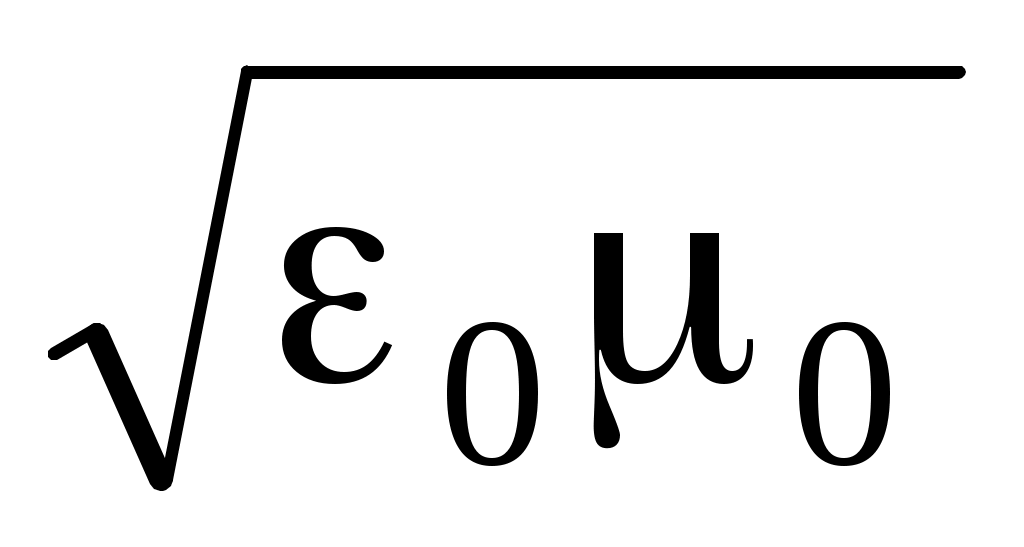 = = 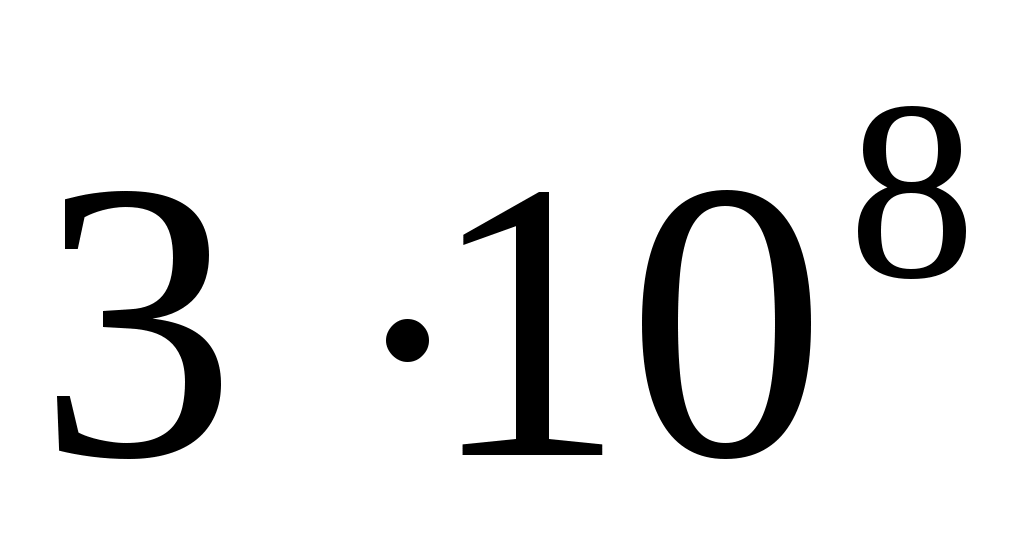 м/c. м/c.
Каждое из уравнений эквивалентно трем скалярным относительно декартовых компонент.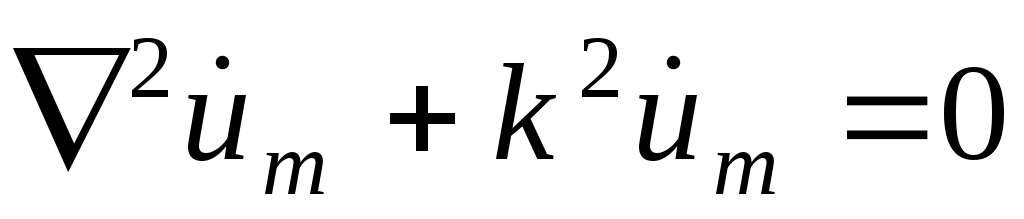 -однородное уравнение Гельмгольца. k = v– волновое число, v – фазовая скорость. -однородное уравнение Гельмгольца. k = v– волновое число, v – фазовая скорость.
Решения векторных уравнений складываются из своих проекций.
Для одномерного процесса, зависящего от координаты z , 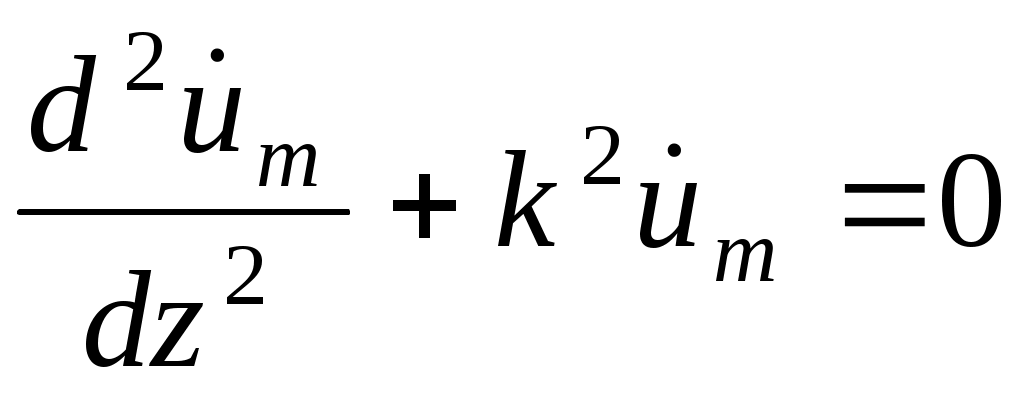
Общее решение этого уравнения 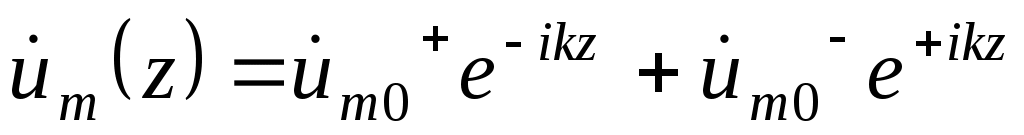
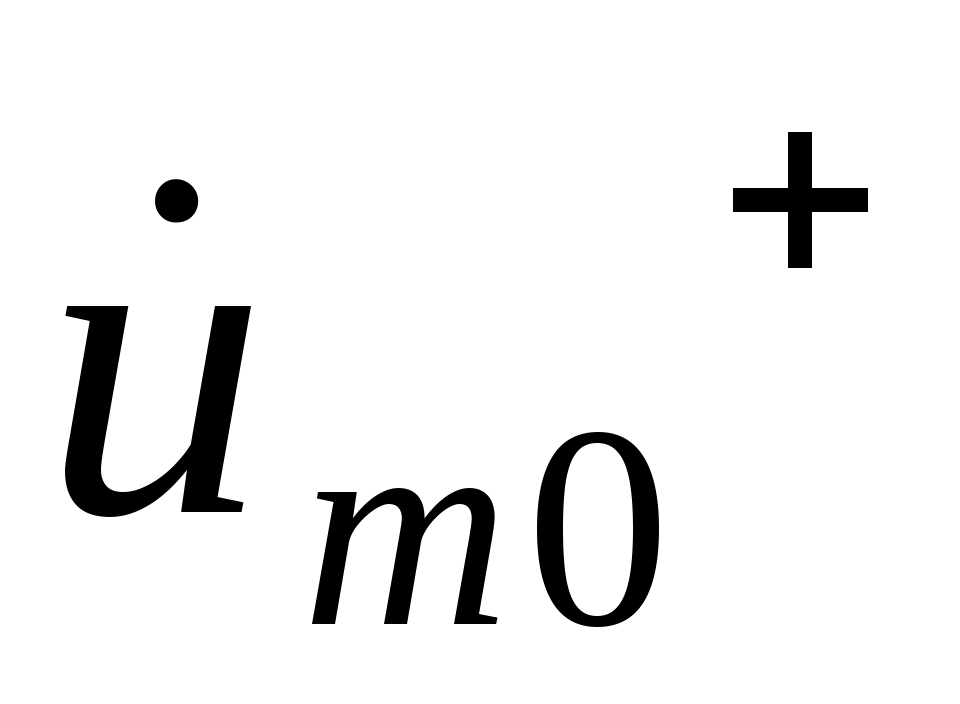 , , 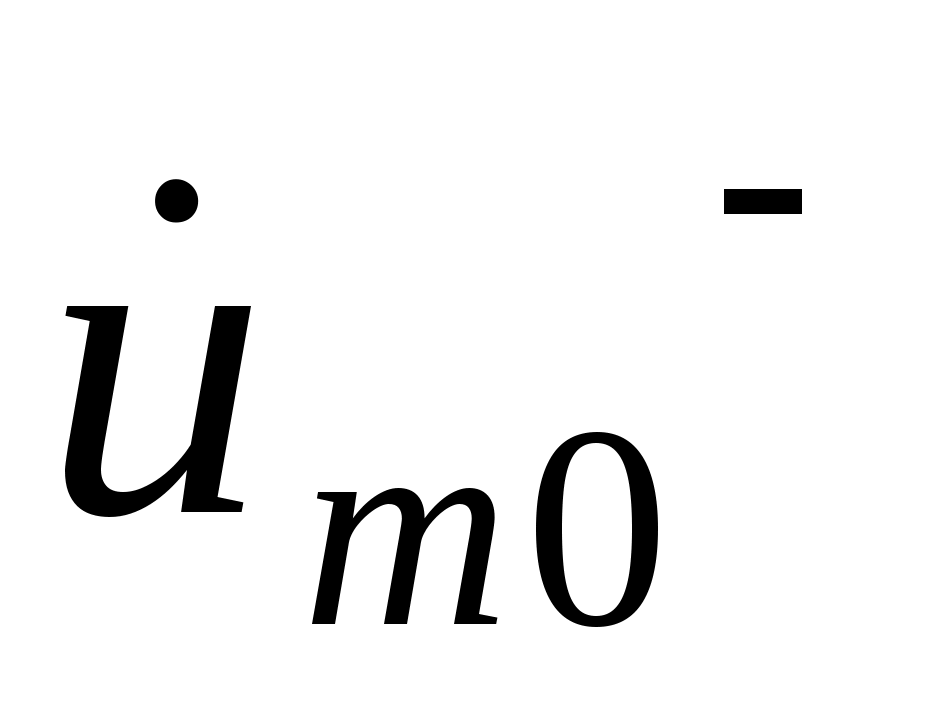 - произвольные комплексные константы. Если положить - произвольные комплексные константы. Если положить
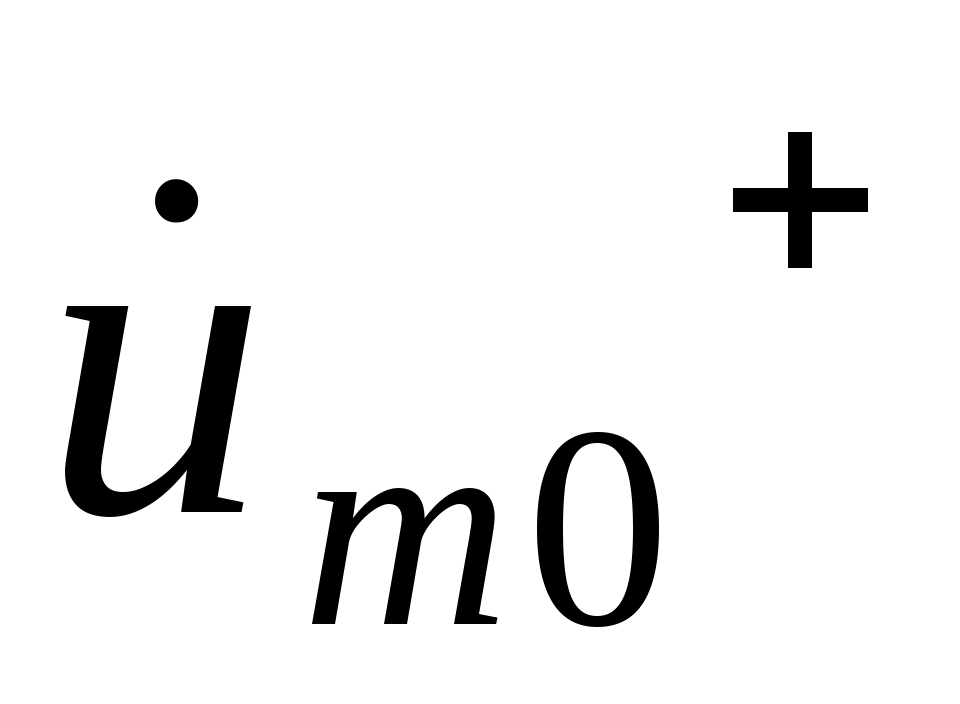 = = 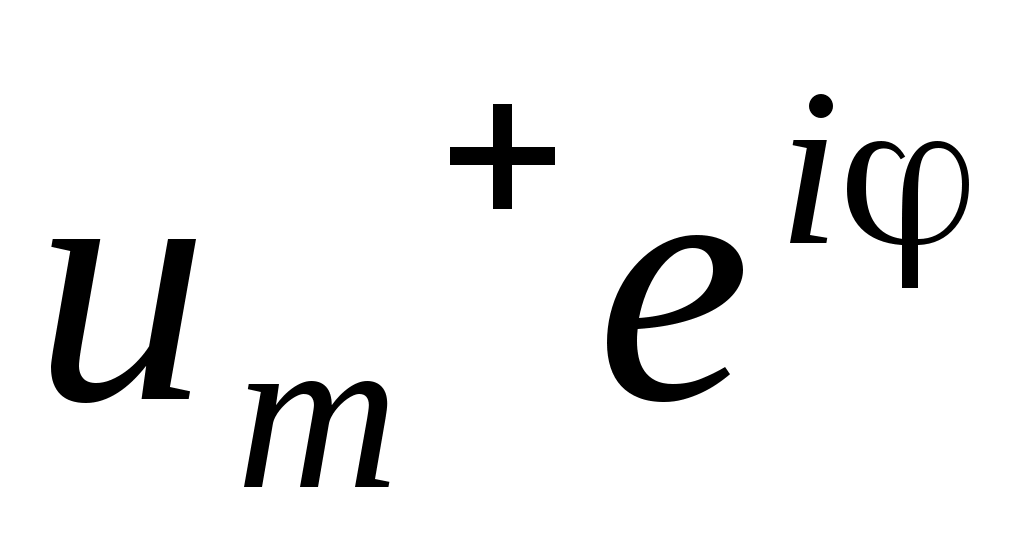 , , 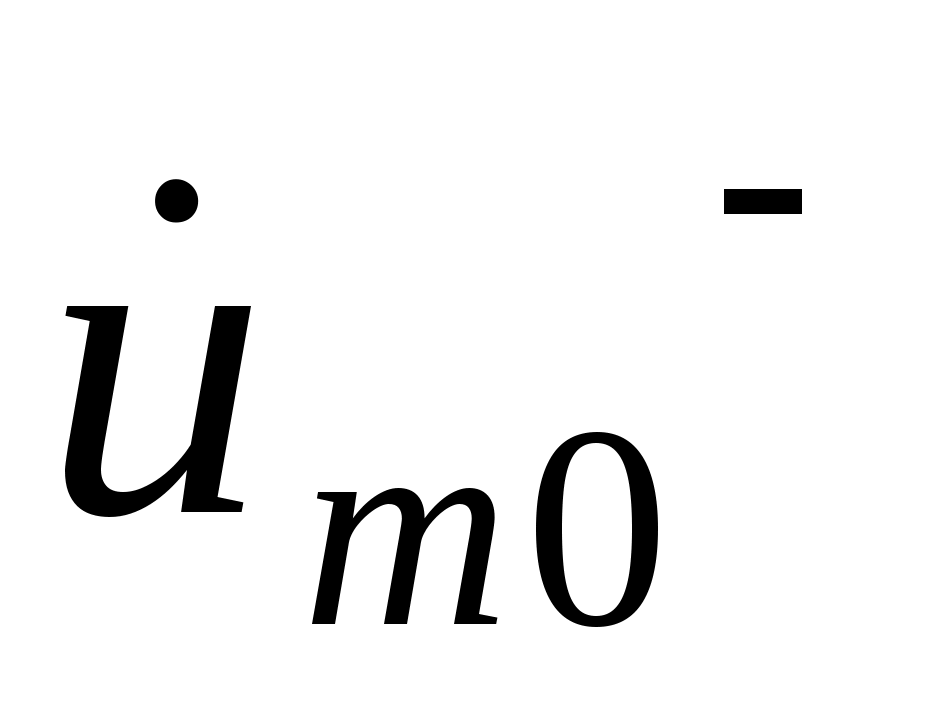 = = 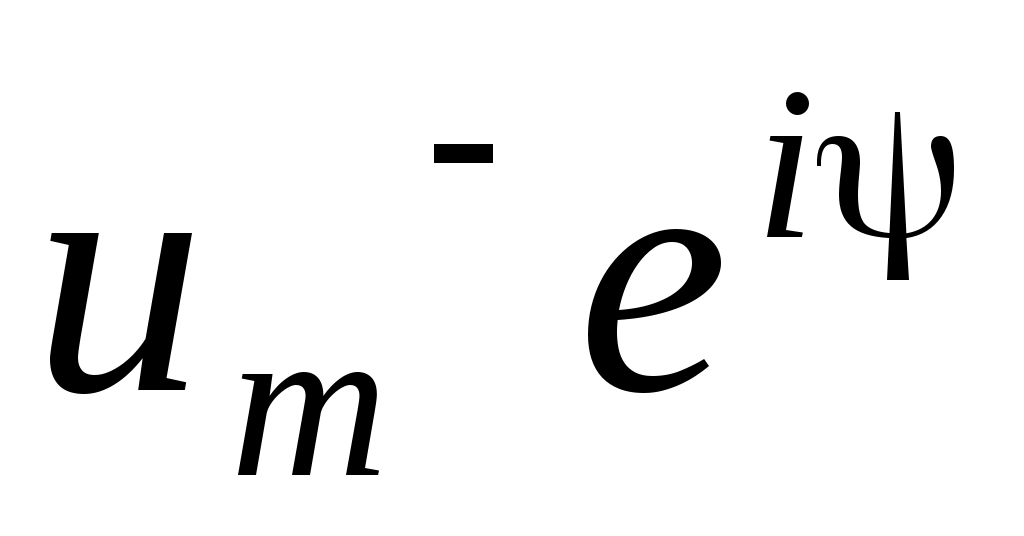 , то при вычислении операции Re , то при вычислении операции Re 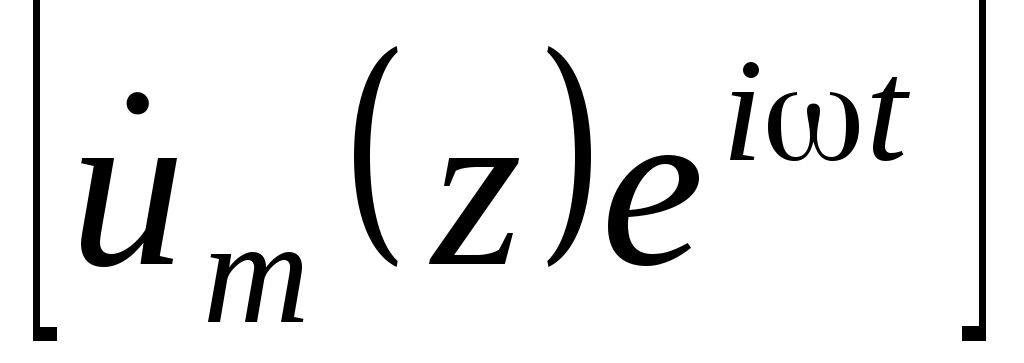 получаем функцию u (z, t) = Um+ cos ( t – kz+ ) + Um- cos ( t + kz + ), которая является решением волнового уравнения. Это – гармонические волны. получаем функцию u (z, t) = Um+ cos ( t – kz+ ) + Um- cos ( t + kz + ), которая является решением волнового уравнения. Это – гармонические волны.
Рассматривая простейшие поля, зависящие только от декартовой координаты z, можно записать решения
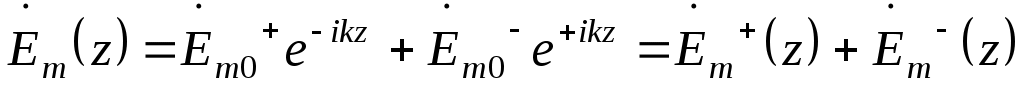
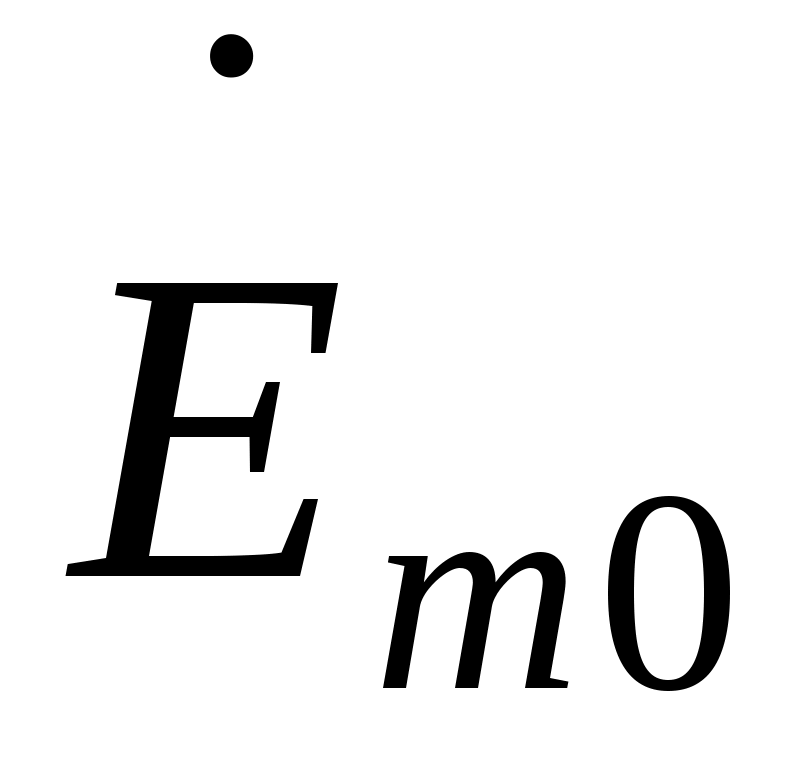 , , 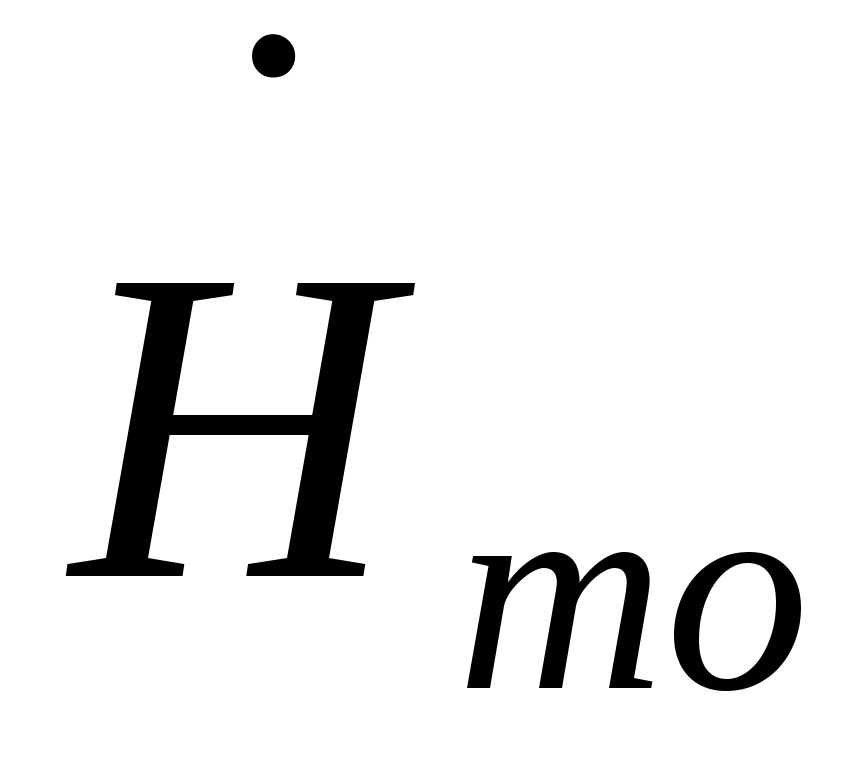 - неопределенные векторные константы. - неопределенные векторные константы.
Компоненты 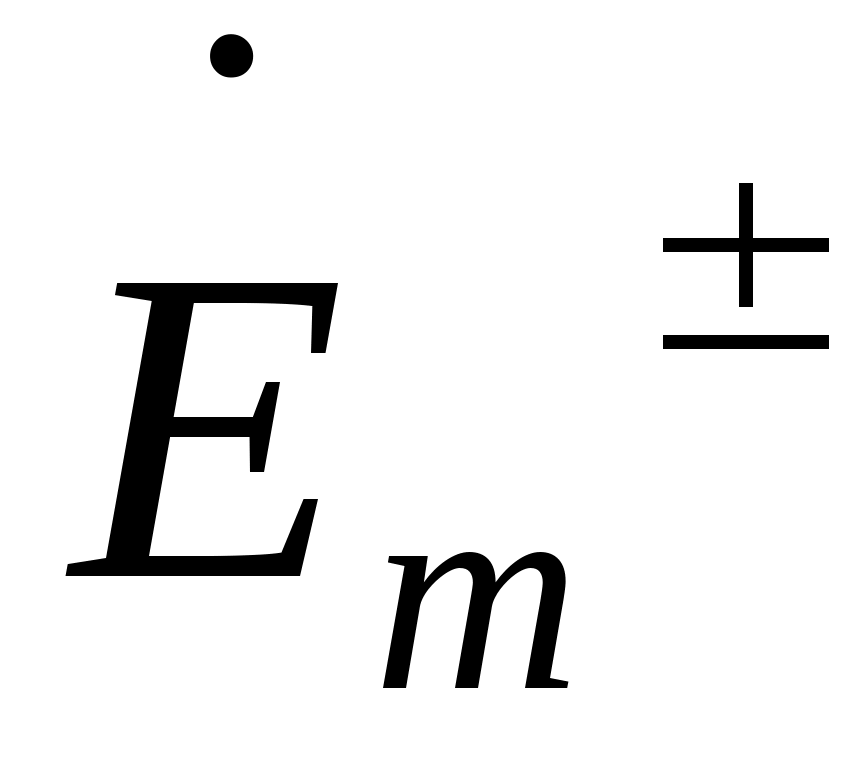 , , 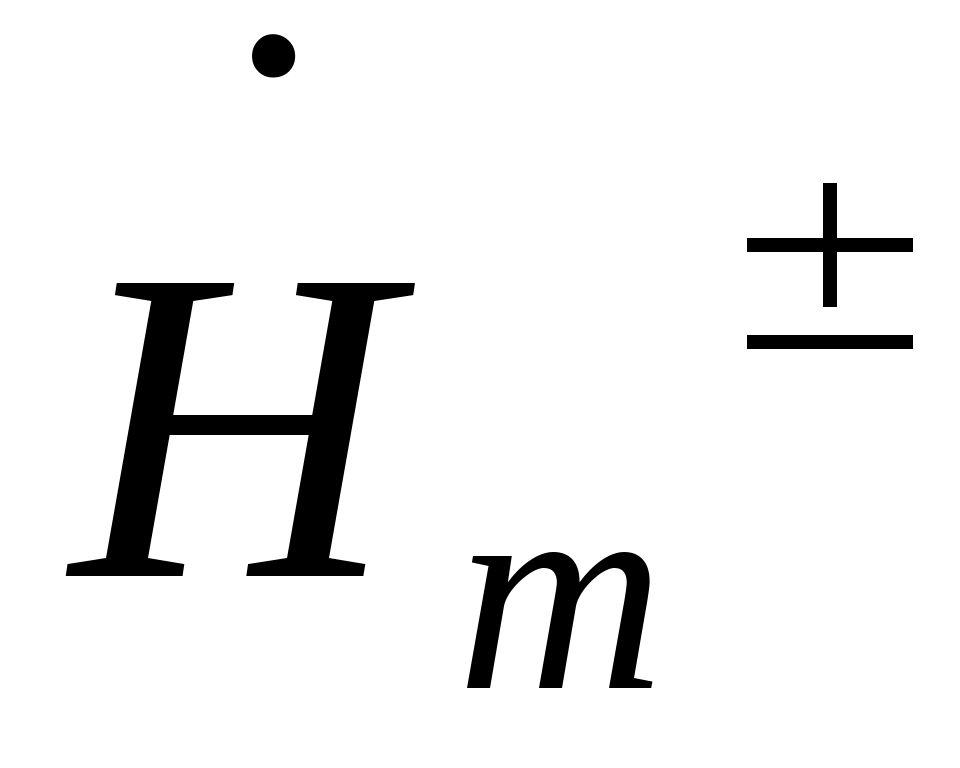 от координатx и y не зависят. от координатx и y не зависят.
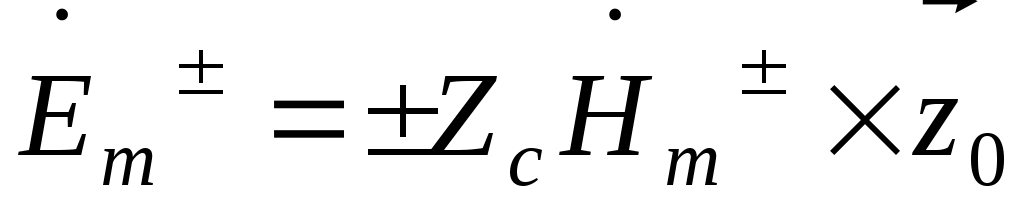
Zc=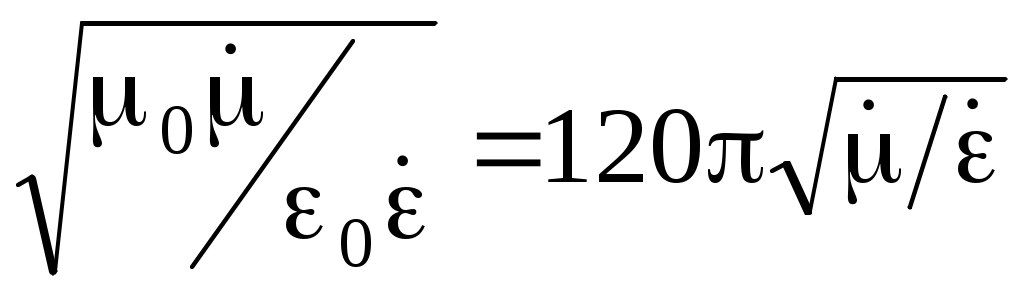 - характеристическое сопротивление волны (отношение поперечных к направлению распространения волны составляющих векторов - характеристическое сопротивление волны (отношение поперечных к направлению распространения волны составляющих векторов и и  ) )
1) векторы 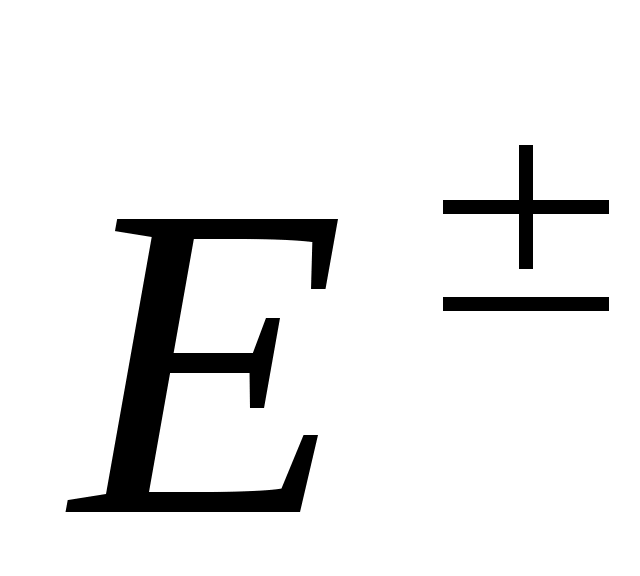 и и 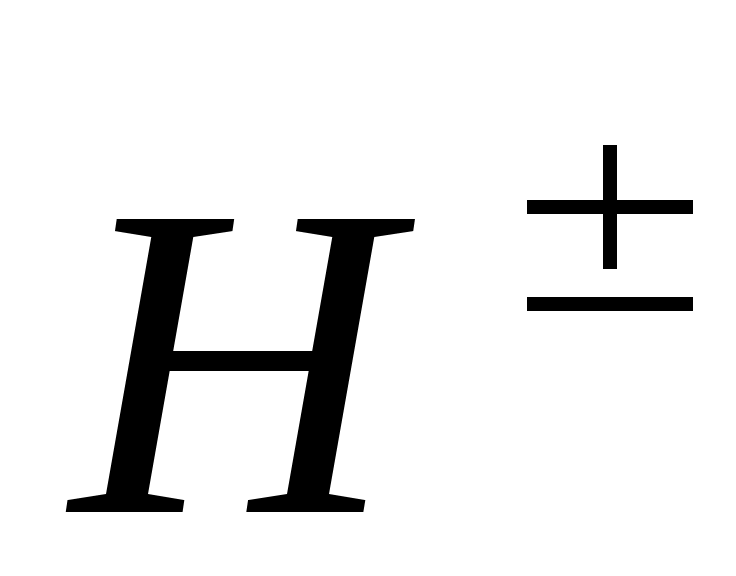 не имеют продольных компонент: не имеют продольных компонент: 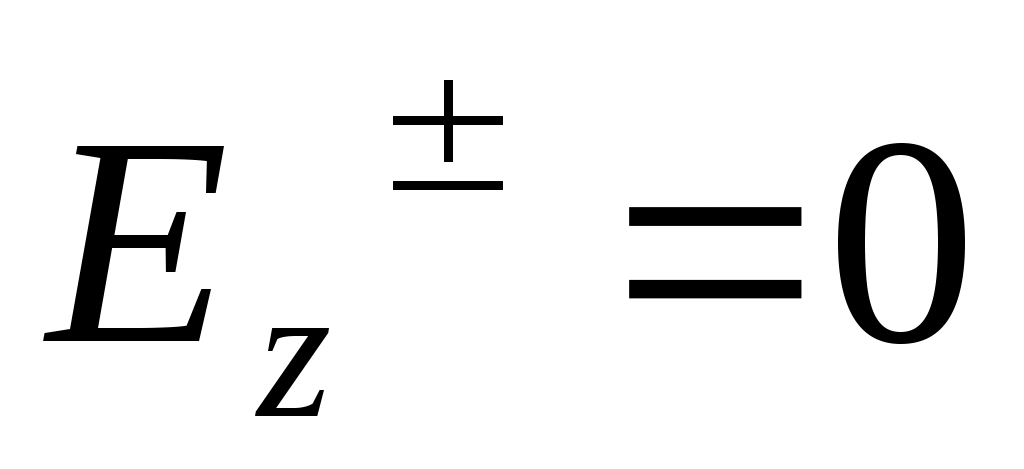 , , 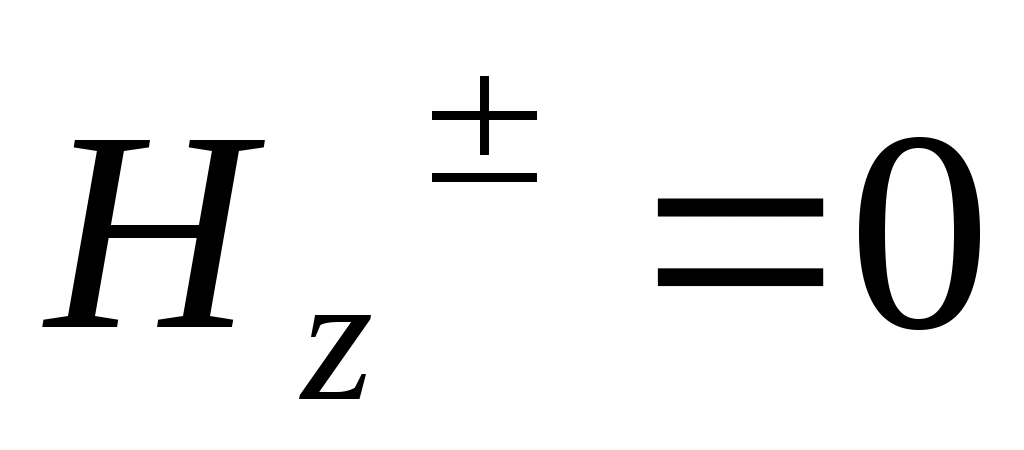 - это поперечная волна; 2) эти векторы ортогональны, т.е. - это поперечная волна; 2) эти векторы ортогональны, т.е. 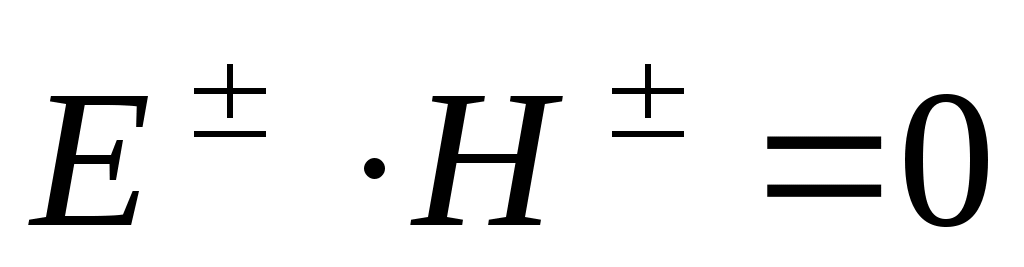 ; ;
3) отношение скалярных величин 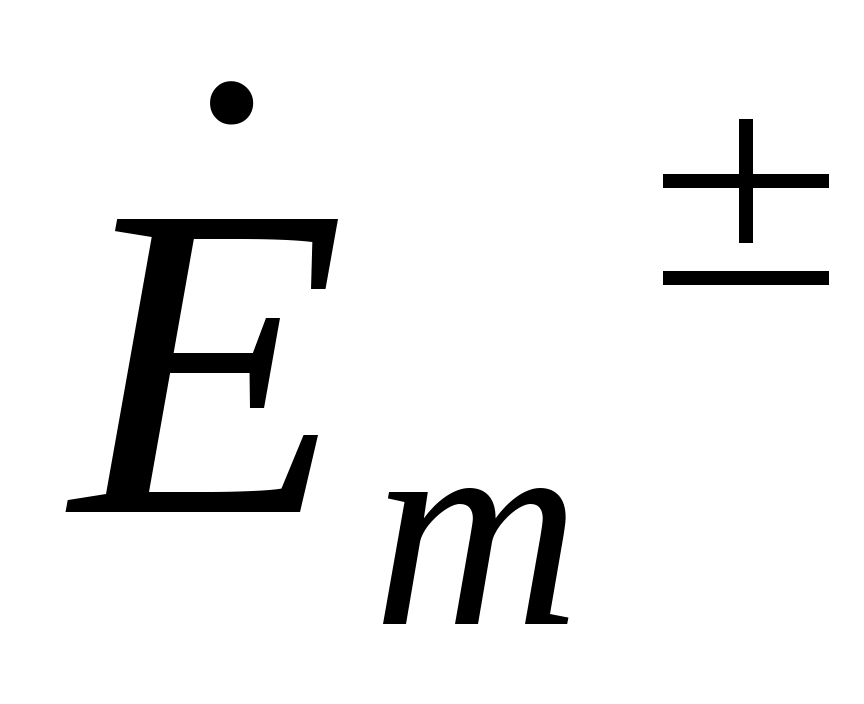 и и 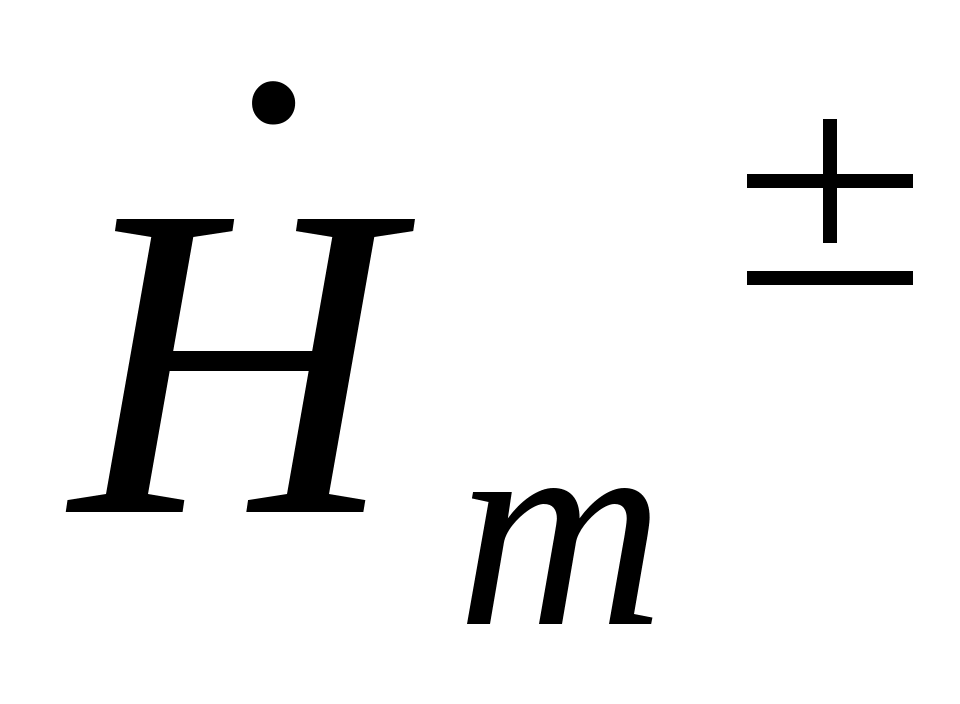 равно Zc. равно Zc.
В рамках метода комплексных амплитуд любой из параметров уравнений Максвелла надо рассматривать на комплексной плоскости.
Проницаемости e и m 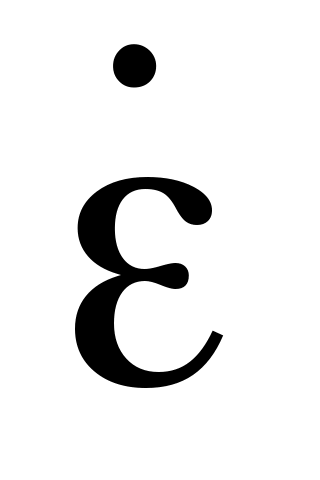 = e’ - i e”, = e’ - i e”, 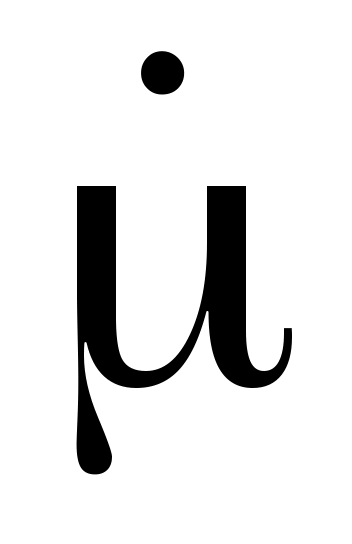 = m’ – i m” = m’ – i m”
Вводя обозначения tg d = e¢¢ ¤ e¢ , tg dM = m¢¢ ¤ m¢, d - угол электрических потерь, dM – угол магнитных потерь, выражения для проницаемостей можно записать 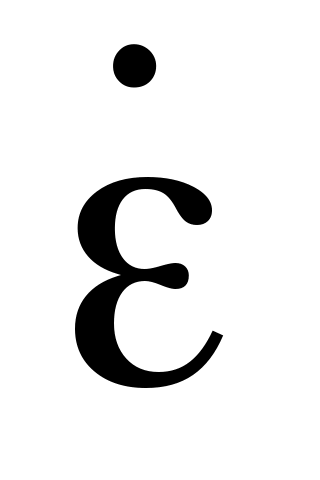 = e¢(1- i tg d), = e¢(1- i tg d), 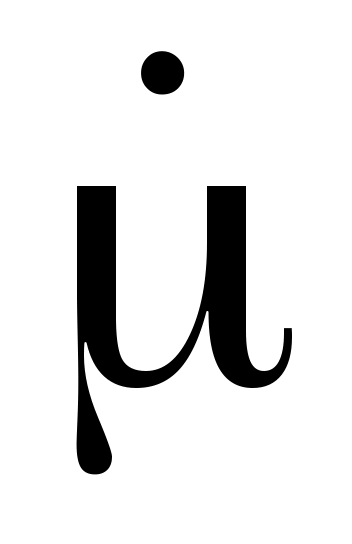 = m¢(1 - i tg dM). Если tg d >>1, среду рассматривают как проводник, для диэлектриков tg d <<1. = m¢(1 - i tg dM). Если tg d >>1, среду рассматривают как проводник, для диэлектриков tg d <<1.
Если проницаемости 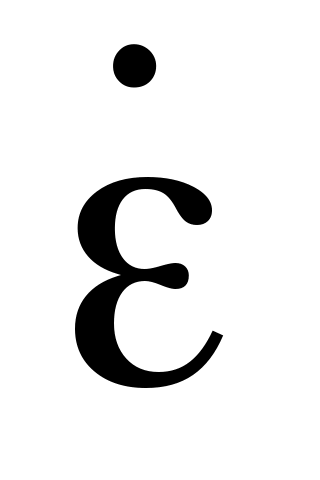 = r , = r , 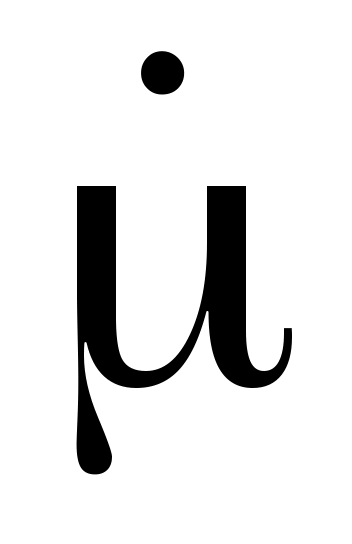 = r – вещественны, то среда не поглощает энергии электромагнитного поля. В этом случае k и Zc= = r – вещественны, то среда не поглощает энергии электромагнитного поля. В этом случае k и Zc= 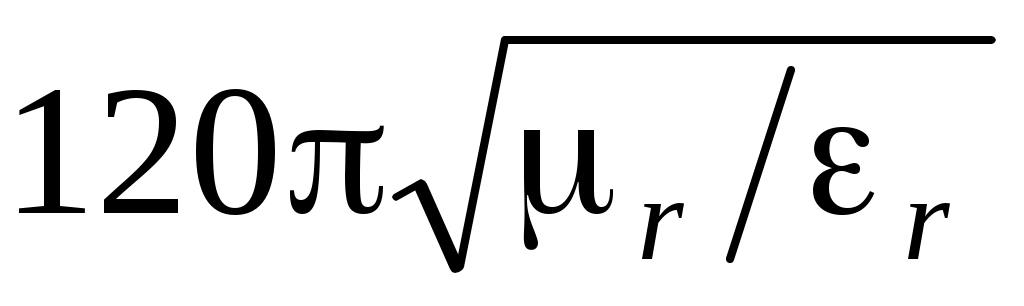 – вещественные. – вещественные.
Если волна распространяется вдоль оси z , а вектор  направлен вдоль оси x, направлен вдоль оси x, 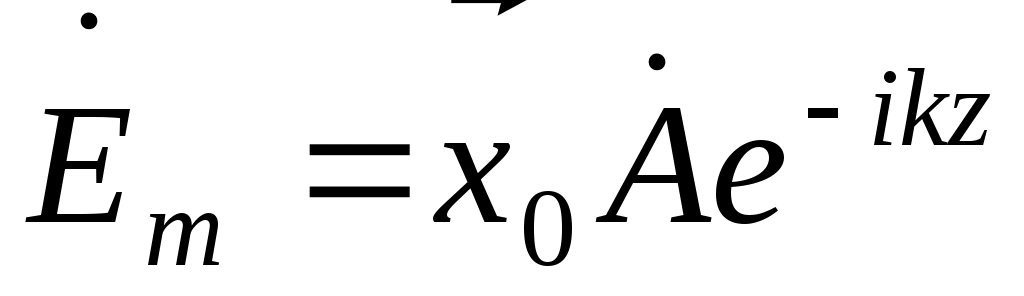 , , 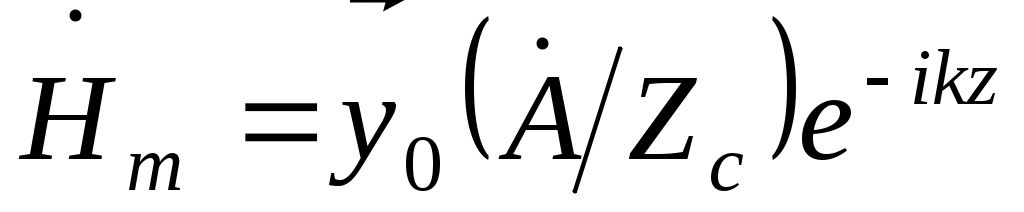
При этом напряженности поля:
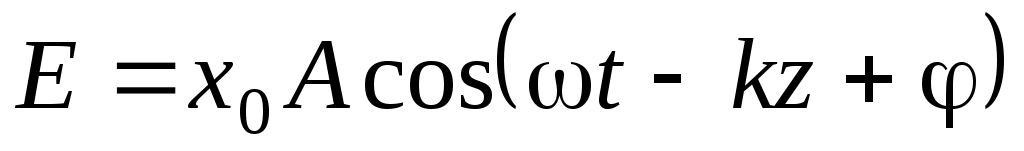 , , 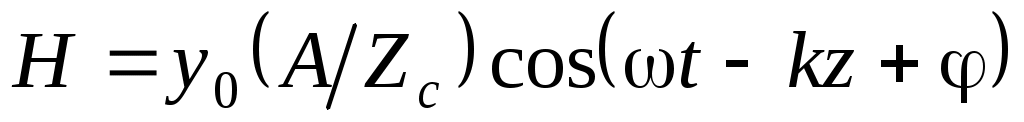 . .
В плоской волне векторы 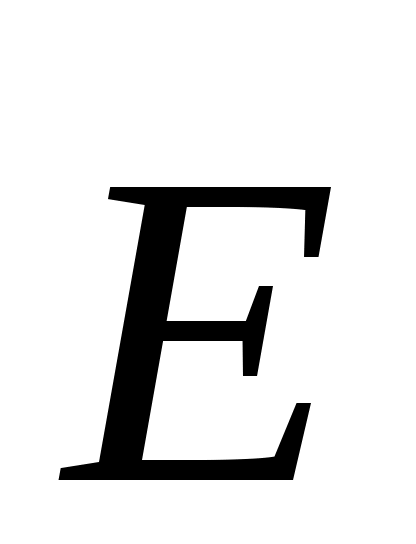 и и  взаимно ортогональны и ортогональны направлению распространения. взаимно ортогональны и ортогональны направлению распространения. 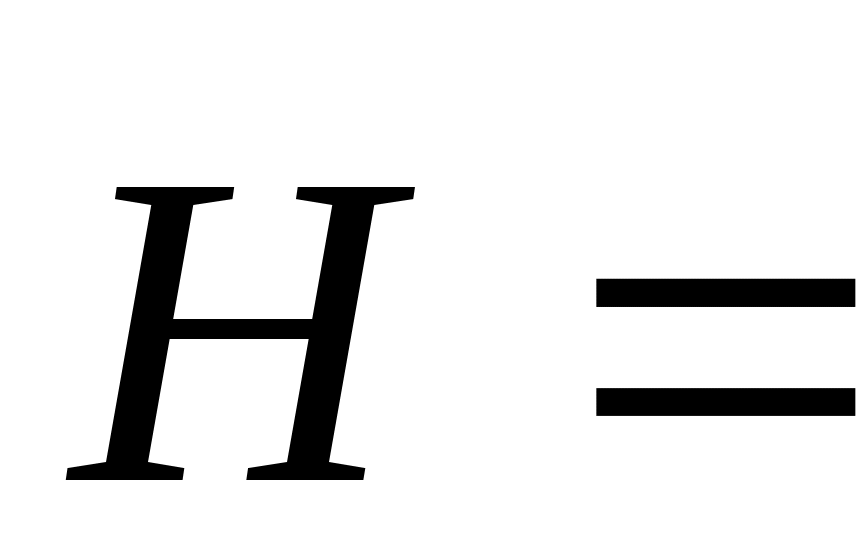 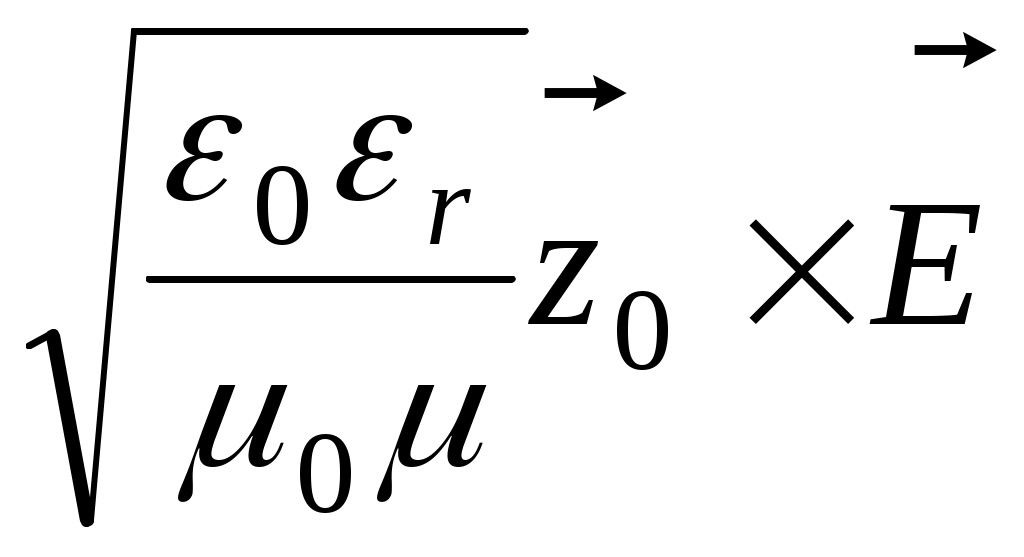
Распространение волны сопровождается переносом энергии. Вектор Пойнтинга 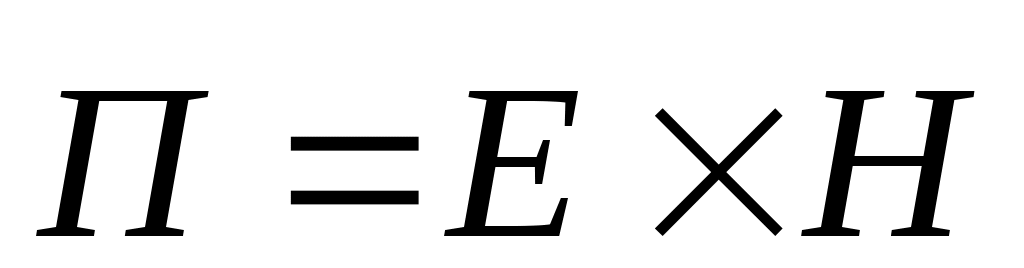 направлен по оси z; направлен по оси z; 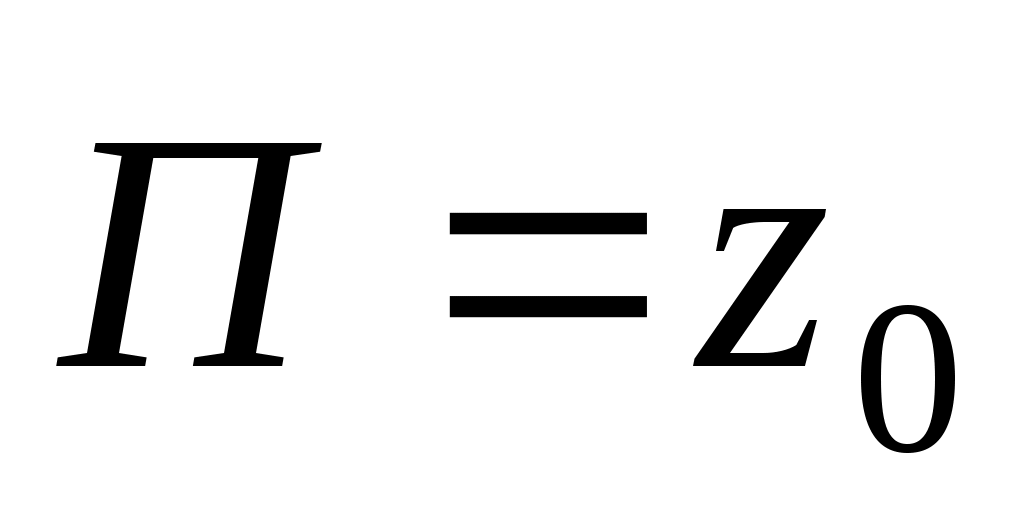 (A2 / Zc) cos2 (t – kz +). (A2 / Zc) cos2 (t – kz +).
В однородной изотропной среде при наличии потерь параметрk следует считать комплексной величиной: k = k- ik.
Тогда для гармонической волны
u(z,t) = Re{Um exp[ i (t – kz +)]} = Um e xp (- k”z) cos (t – k’z +).
Если k” >0 – это затухающая волна. k” – коэффициент затухания.
k’ = /v = 2 - коэффициент фазы. Фазовую скорость при этом рассматривают как скорость смещения фронта волны с нулевой амплитудой. Длина волны уже не является периодом, но определяется по нулям функции.
Для затухающей электромагнитной волны 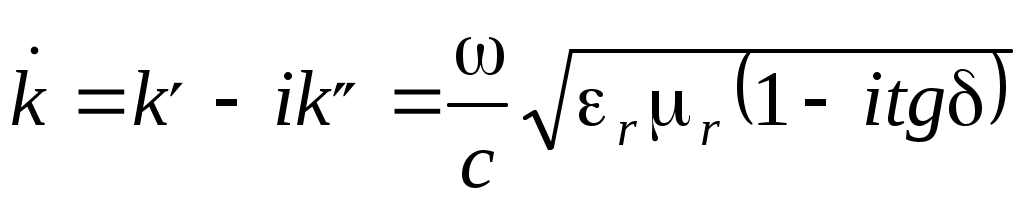 . (Считаем, что . (Считаем, что 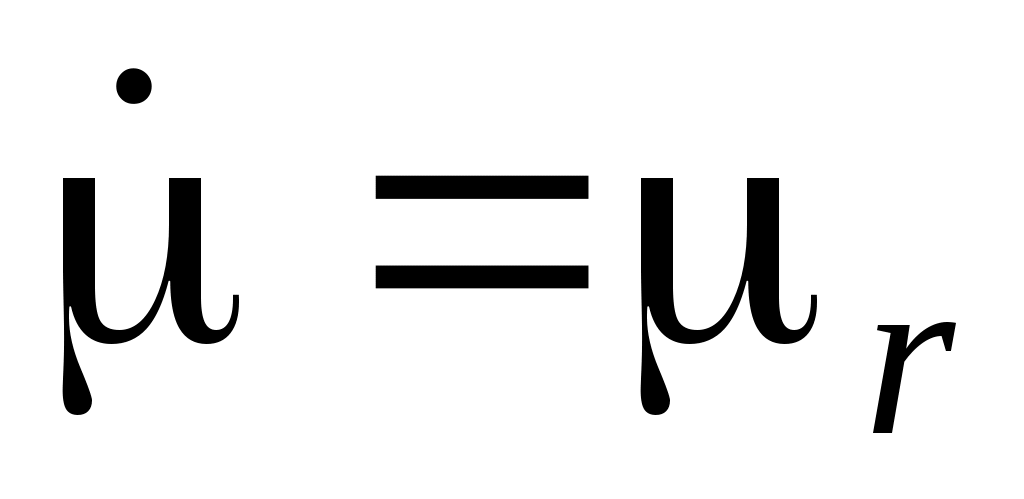 ) )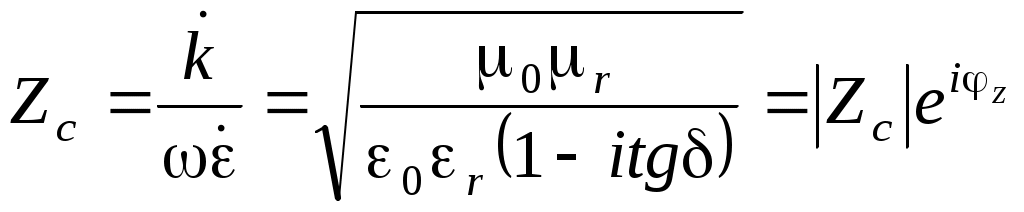 ; ; 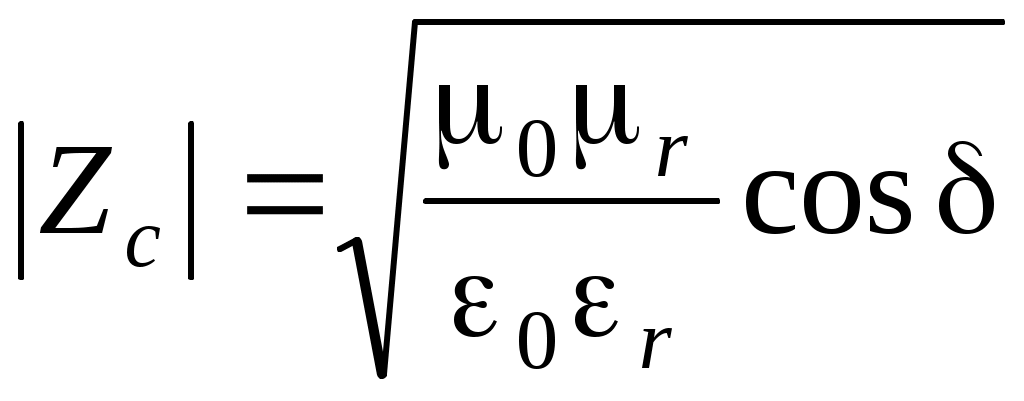 ; ;
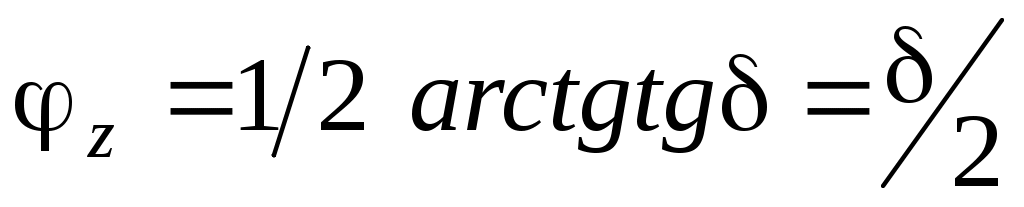 . .
Затухающая электромагнитная волна 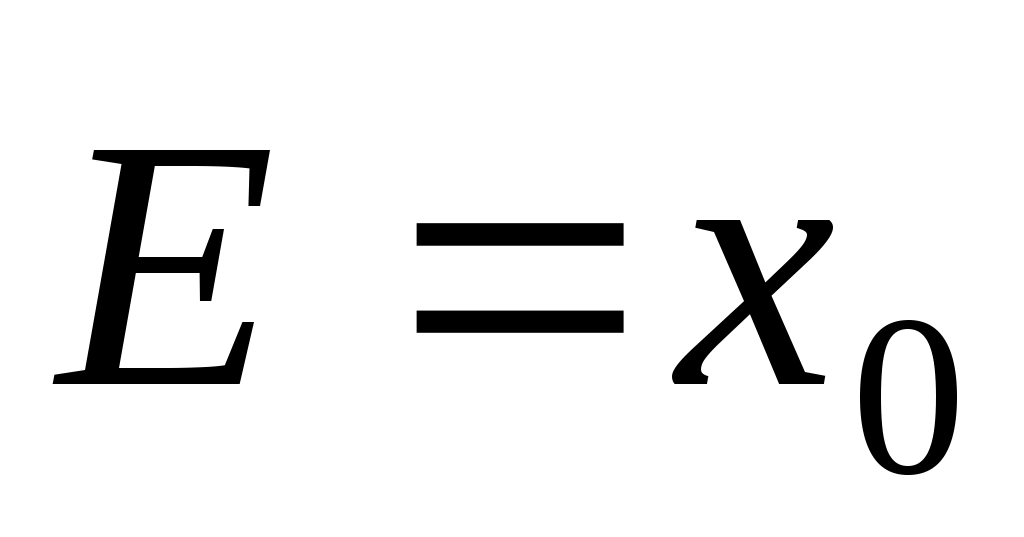 A exp (- k”z) cos (t – k’z+), A exp (- k”z) cos (t – k’z+), 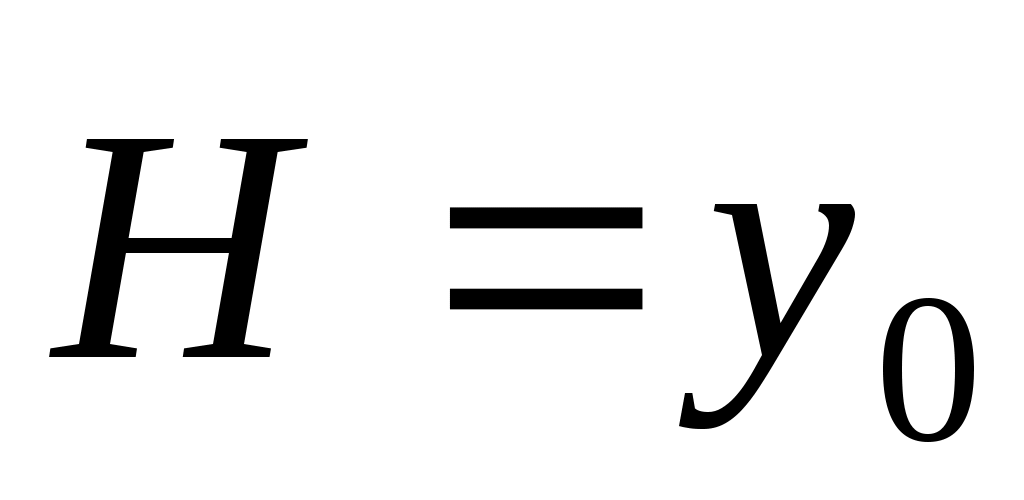 (A/Zc)exp (- k”z) cos(t – k’z + - z) - распространяется вдоль направленияz с фазовой скоростью v = / k’; характеристическое сопротивление Zc = Zc’+ iZc ” = Zc exp (i z), (A/Zc)exp (- k”z) cos(t – k’z + - z) - распространяется вдоль направленияz с фазовой скоростью v = / k’; характеристическое сопротивление Zc = Zc’+ iZc ” = Zc exp (i z), 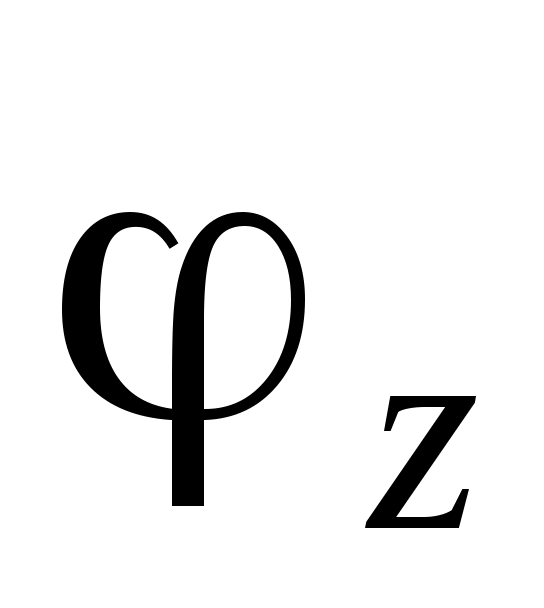 - фазовый сдвиг между векторами - фазовый сдвиг между векторами  и и . .
Распространение волны сопровождается переносом энергии. Выражение мгновенного значения вектора Пойнтинга (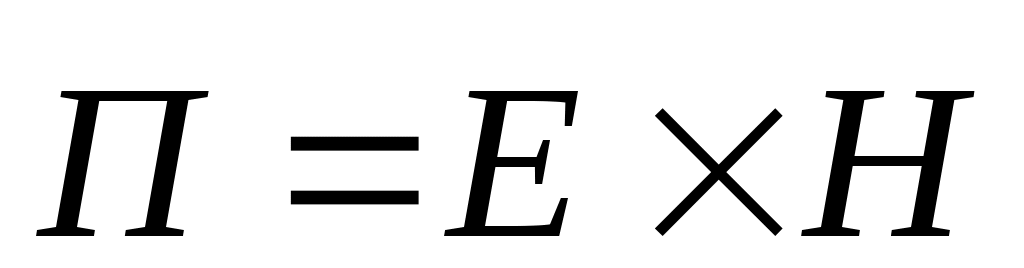 ) для волны в поглощающей среде ) для волны в поглощающей среде
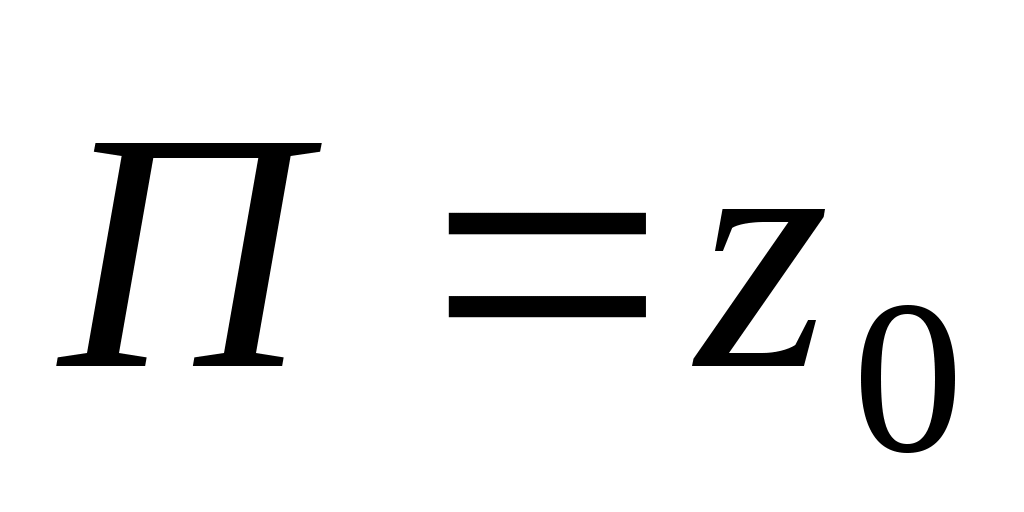 (A2 / Zc ) e xp (- 2k”z) cos ( t – k’z +) cos ( t – k’z + - z) = (A2 / Zc ) e xp (- 2k”z) cos ( t – k’z +) cos ( t – k’z + - z) =
= 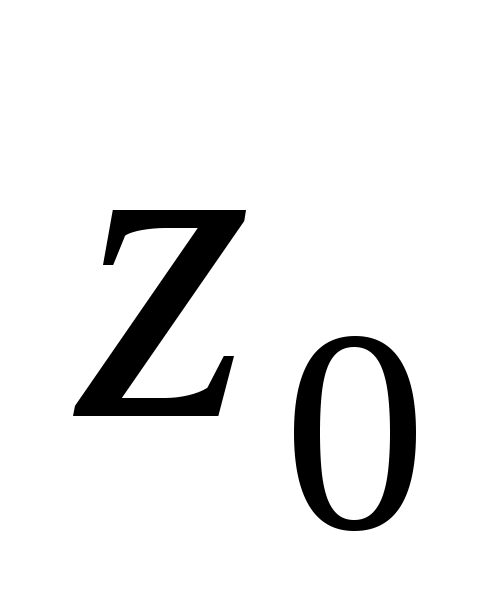 (A2 / 2 Zc ) e xp (- 2k”z) {cos z + cos [2 ( t – k’z +) - z]} (A2 / 2 Zc ) e xp (- 2k”z) {cos z + cos [2 ( t – k’z +) - z]}
При усреднении во времени ( 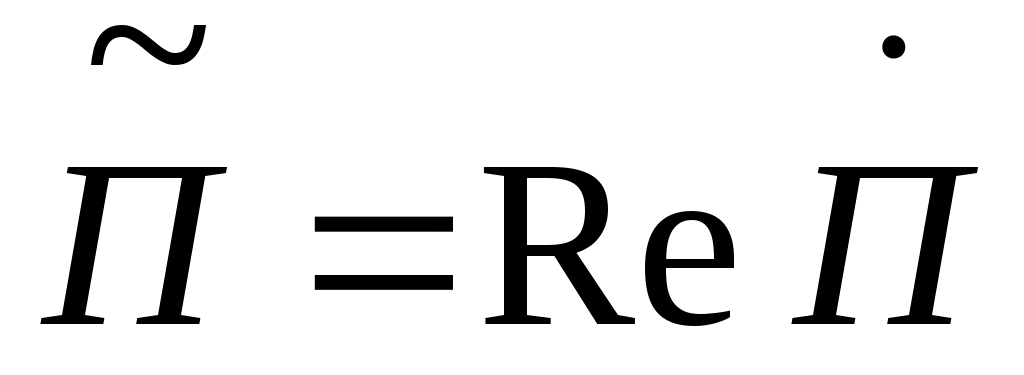 , , 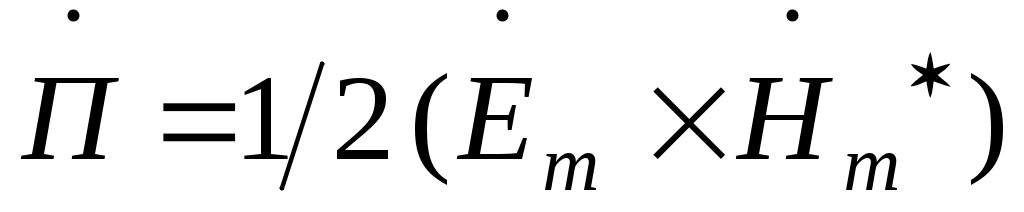 ) )
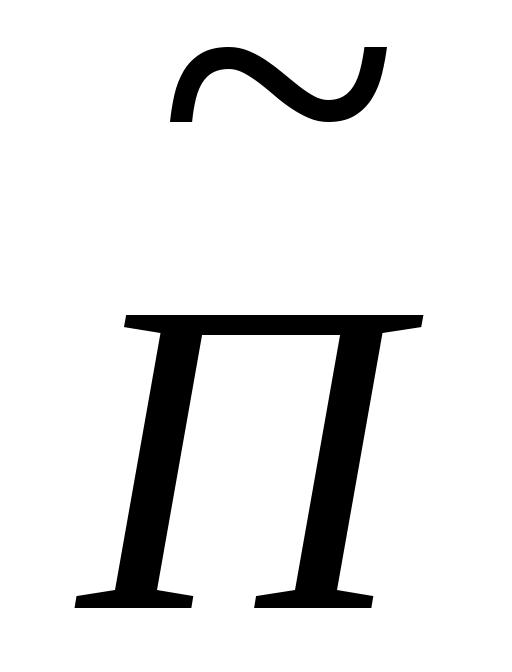 = = 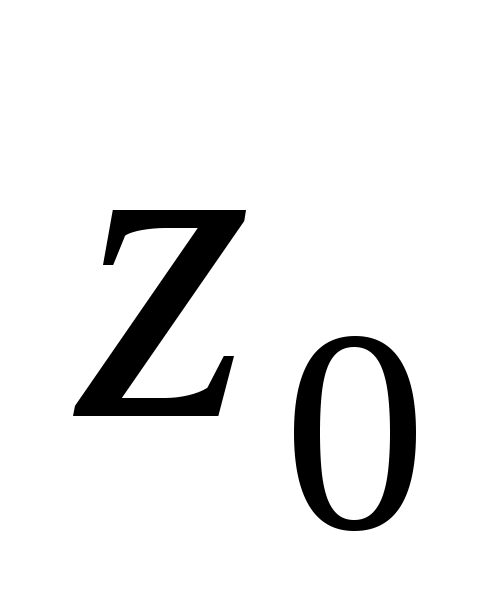 (A2/2Zc)exp(-2k”z)cosz - средняя плотность потока энергии экспоненциально убывает вдоль z. (A2/2Zc)exp(-2k”z)cosz - средняя плотность потока энергии экспоненциально убывает вдоль z.
Запишем коэффициент затухания и коэффициент фазы для волны в диэлектрике и в проводнике.
k = k’ – ik” = k exp [ -i ( м ] = [(1 – i tg ) (1 – i tg м)]1/2,
где k = ( с ) = ( с ) ( )1/2 = ( с ) ( )1/2
В большинстве случаев магнитные потери в среде не учитывают (” = 0). При этом k = K (1 – i tg )1/2
В диэлектрике tg << 1.
Приближенные формулы k’ K = ( с) ( )1/2, k” K/2 tg =
= ½ ( с) ( )1/2 tg .
Характеристическое сопротивление волны в том же приближении
Zc = Zc0 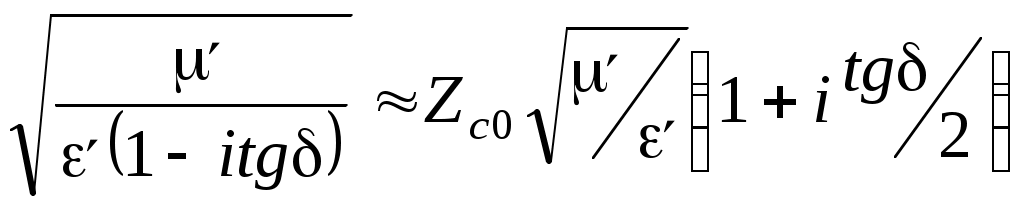 . . 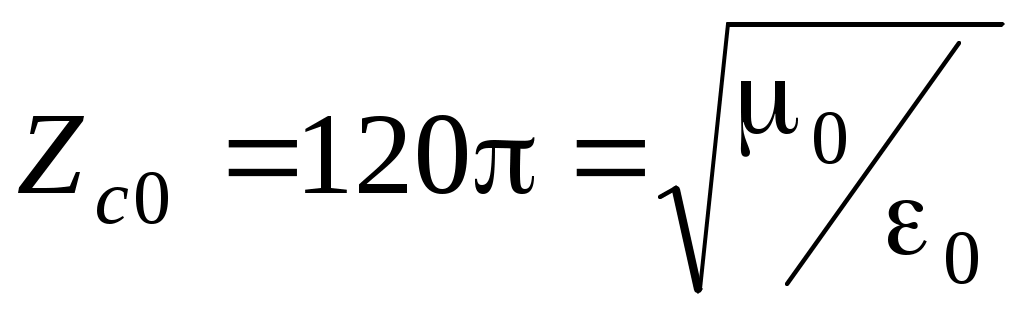 . .
В проводнике tg >> 1. k K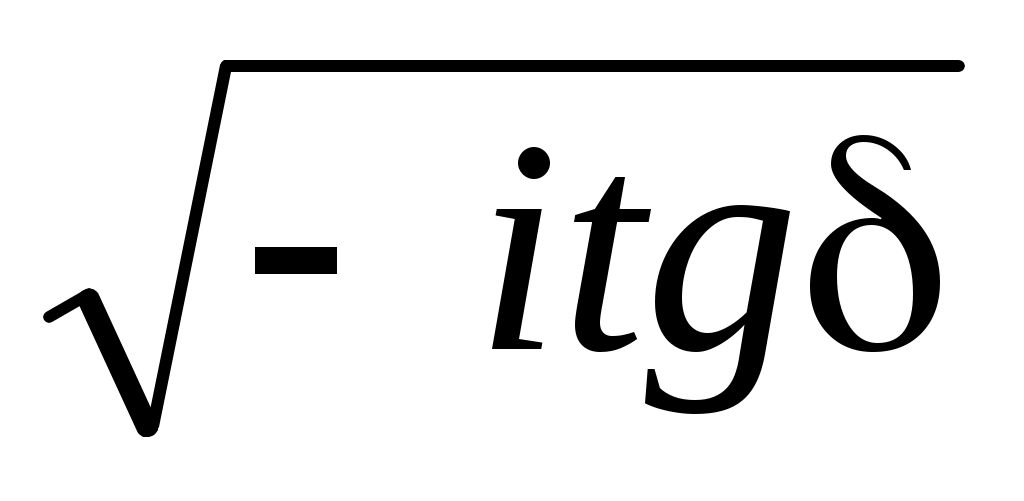 = (1-i)K = (1-i)K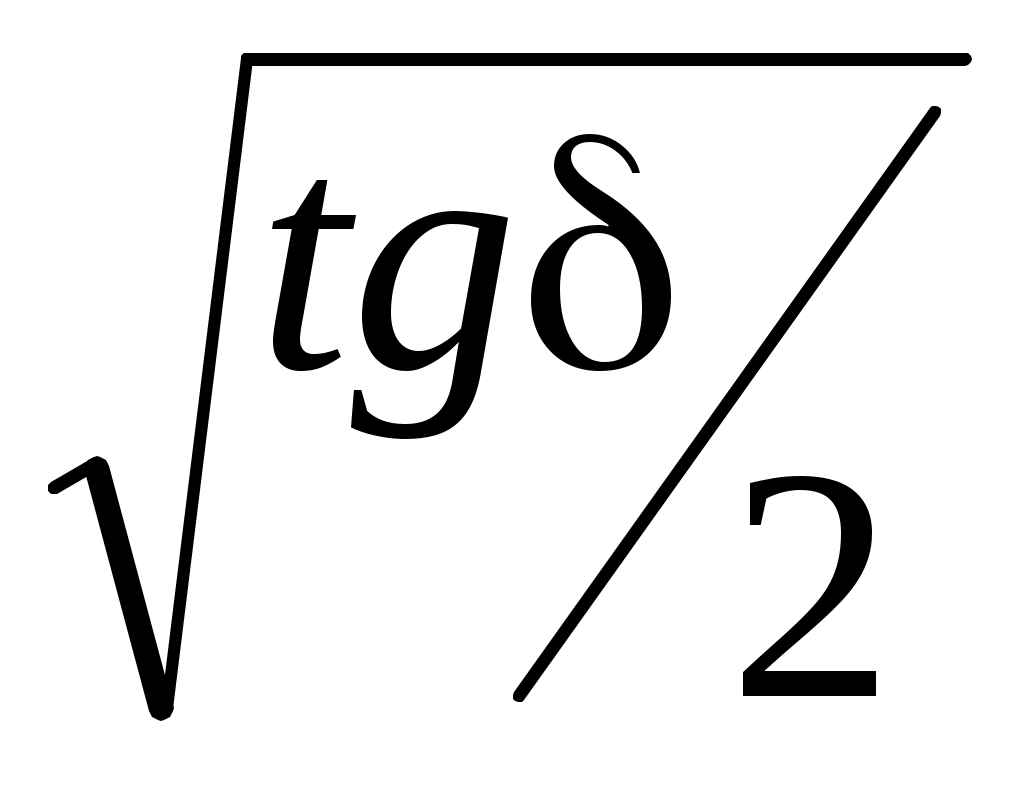 . . 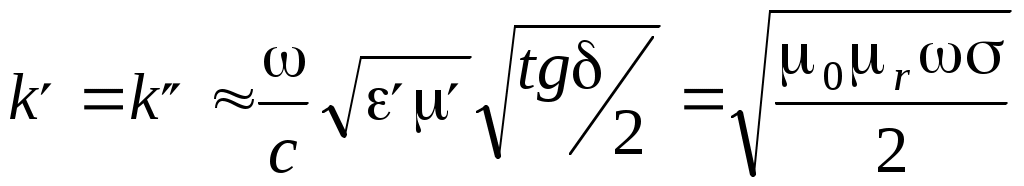 ; ; 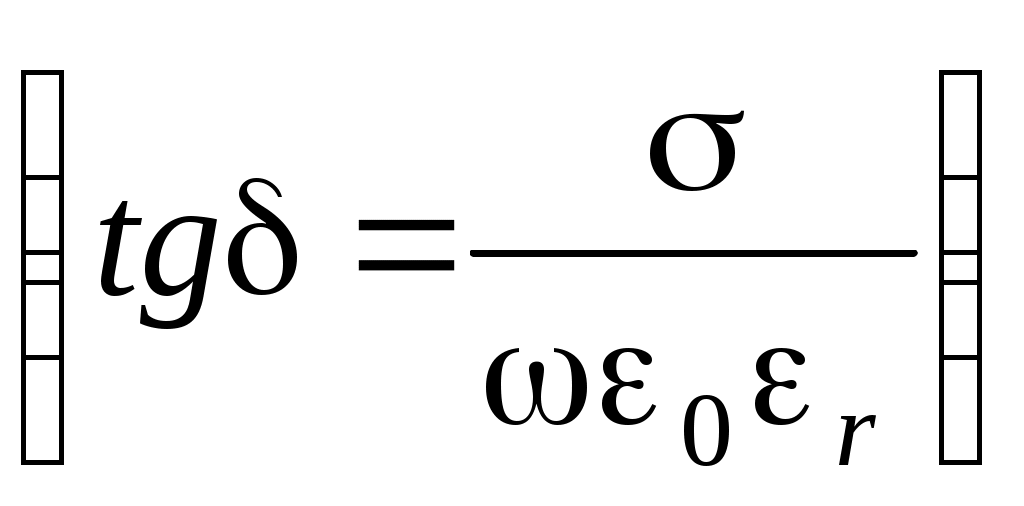
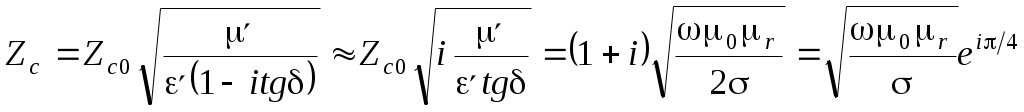
Пусть Em(z) – амплитуда напряженности электрического поля в точке с координатой z. Em (z+l) – амплитуда в точке ( z + l ). Отношение Em(z) /Em (z+l) = exp (k”l) – показывает во сколько раз уменьшается амплитуда волны при прохождении ею расстоянияl. Затухание измеряется в неперах или в децибеллах:
ln [Em(z) / Em (z+l)] = k”l [неп], 20lg [Em(z) / Em (z+l) ] = k”l 20 lg e 8,69 k”l [дБ ]. Расстояние 0, при прохождении которого электромагнитное поле ослабевает в е раз, называют глубиной проникновения поля в среду (толщиной скин-слоя). 0 = 1/ k" = 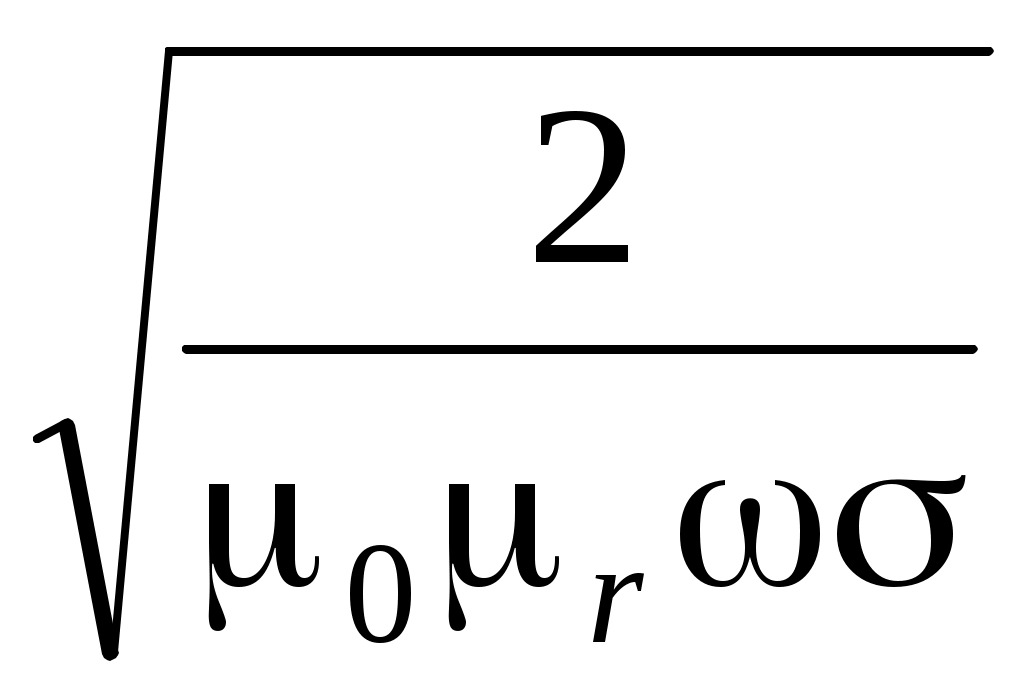 , 0 зависит от частоты. , 0 зависит от частоты.
Рассмотрим пример.
Однородная плоская волна 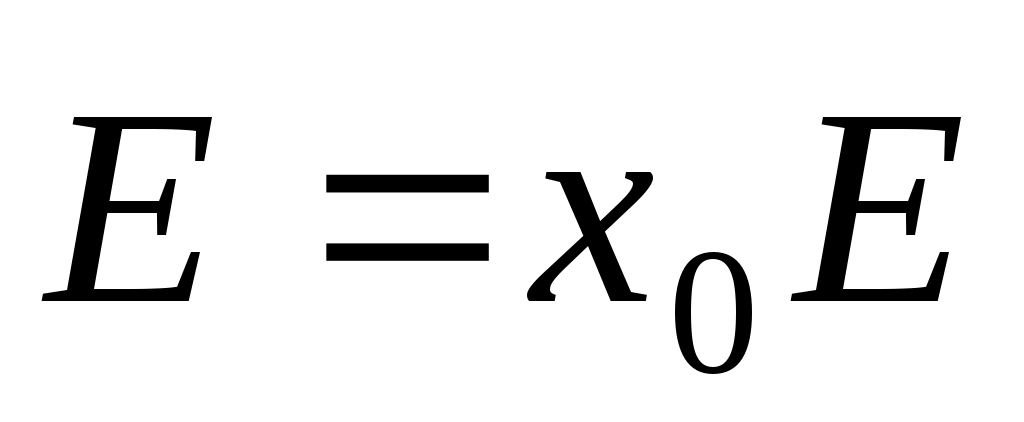 распространяется в среде без потерь ( распространяется в среде без потерь (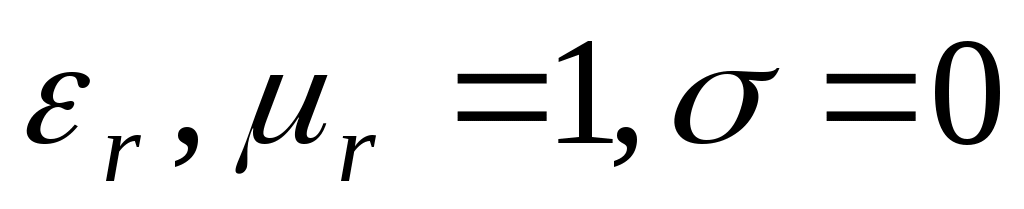 ) в направлении z. Предполагая, что модуль вектора Е – гармоническая функция частоты f имеет максимальное значение Е0 при t = 0 и z =l, записать выражение для векторов ) в направлении z. Предполагая, что модуль вектора Е – гармоническая функция частоты f имеет максимальное значение Е0 при t = 0 и z =l, записать выражение для векторов  и и  для любых t и z и определить точку, где Е имеет положительный максимум в момент времени для любых t и z и определить точку, где Е имеет положительный максимум в момент времени
t = t1.
Запишем 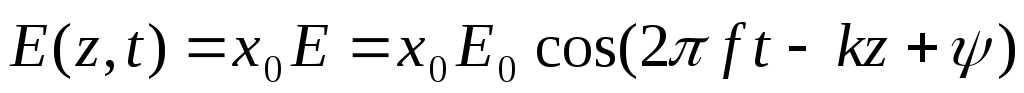 . .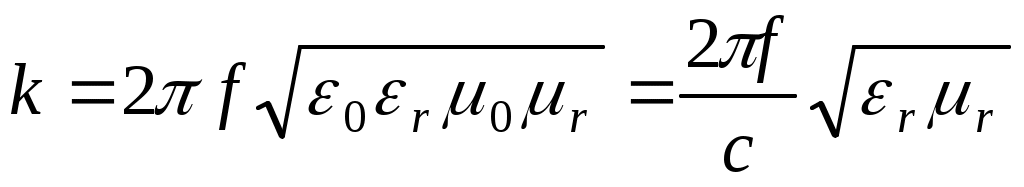 - волновое число. Амплитуда вектора Е принимает максимальные значения, когда аргумент косинуса (2ft – kz + ) = 2 n. Приn = 0 по условию задачи, в частности, при t= 0, z= l. Значит = kl. Если максимального значения косинус достигает в момент t = t1, это соответствует значениям - волновое число. Амплитуда вектора Е принимает максимальные значения, когда аргумент косинуса (2ft – kz + ) = 2 n. Приn = 0 по условию задачи, в частности, при t= 0, z= l. Значит = kl. Если максимального значения косинус достигает в момент t = t1, это соответствует значениям 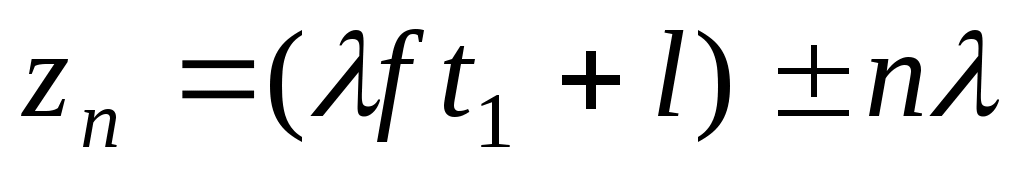 , т.е. точкам, отстоящим друг от друга на длину волны . Таким образом , т.е. точкам, отстоящим друг от друга на длину волны . Таким образом 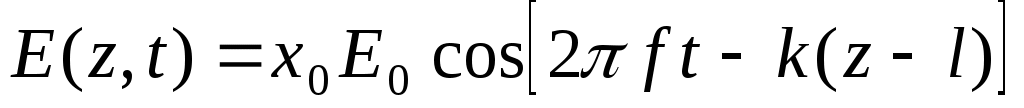 . .
Вектор  волны ортогонален вектору волны ортогонален вектору  и направлению распространения волны. и направлению распространения волны. 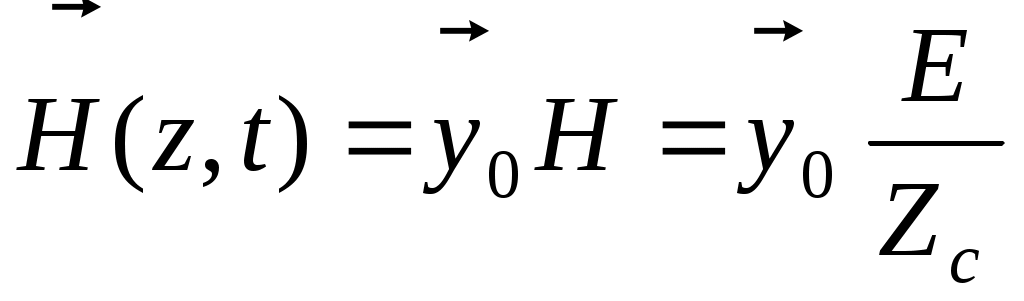 . Zc = . Zc = 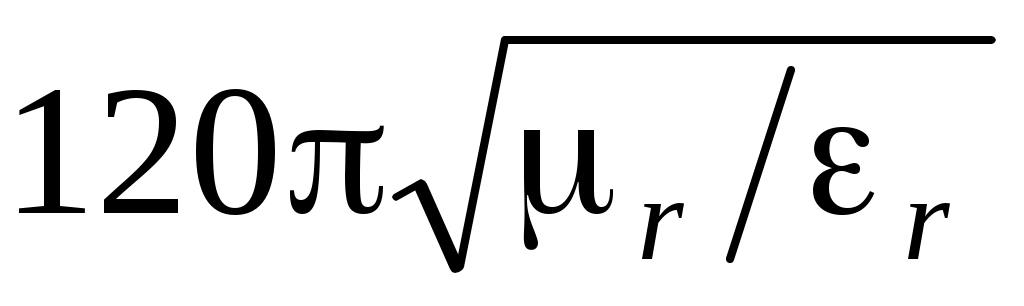 . Следовательно, . Следовательно,
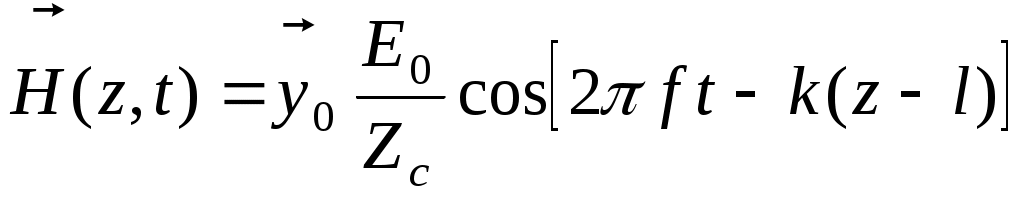 . .
Поляризация волн. Ориентация векторов  и и  относительно осей x, y зависит от источника. Пусть вектор относительно осей x, y зависит от источника. Пусть вектор  имеет одну составляющую Ex. Тогда поле такой плоской волны в среде без потерь определяется формулами имеет одну составляющую Ex. Тогда поле такой плоской волны в среде без потерь определяется формулами
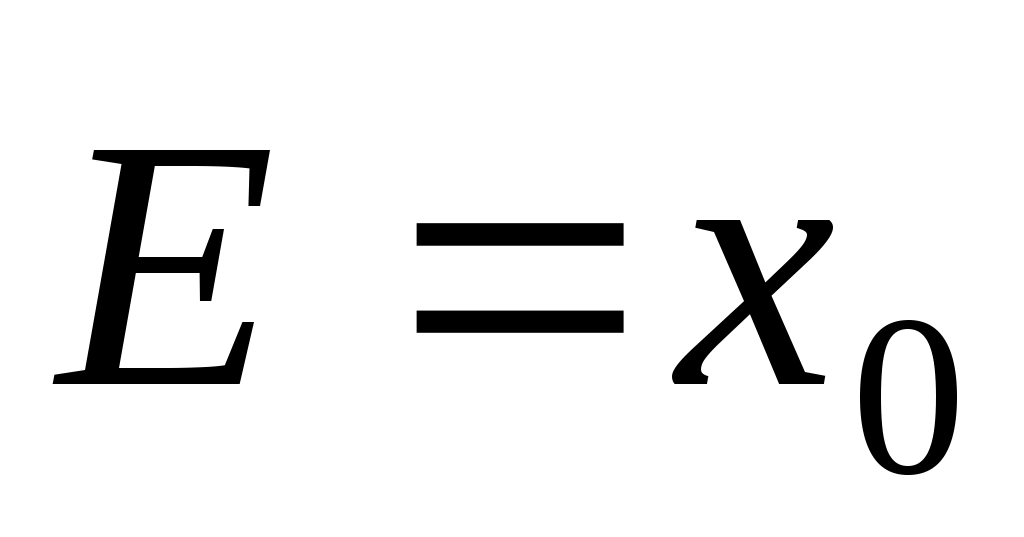 E0 cos ( t – kz + ), E0 cos ( t – kz + ), 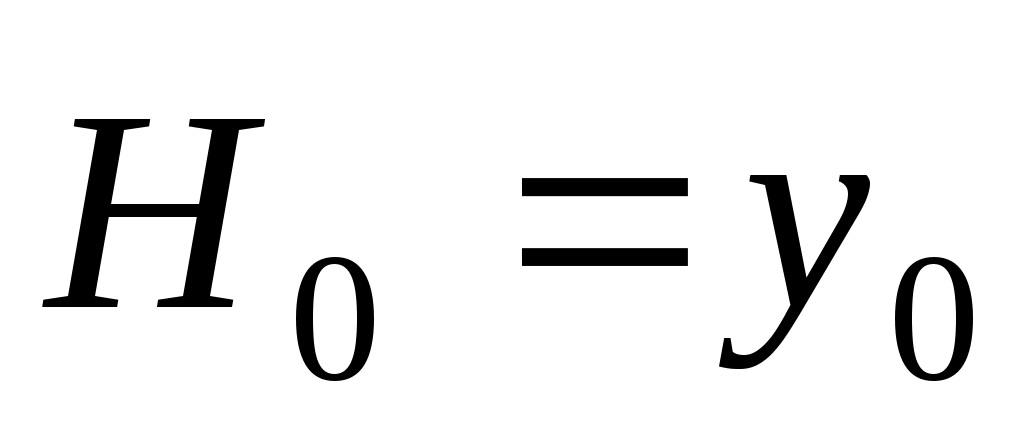 (E0/ Zc) cos ( t – kz + ), (E0/ Zc) cos ( t – kz + ),
- начальная фаза векторов  и и  , т.е. фаза в точке z= 0 при t= 0. , т.е. фаза в точке z= 0 при t= 0.
В фиксированной точке пространства (z = const) конец вектора  с течением времени перемещается вдоль отрезка прямой линии, величина вектора с течением времени перемещается вдоль отрезка прямой линии, величина вектора  изменяется от Е0 до (- Е0). Это – линейно поляризованная волна. изменяется от Е0 до (- Е0). Это – линейно поляризованная волна.
Плоскость, проходящая через вектор  и направление распространения (в рассматриваемом случае - пл. xoz), называется плоскостью поляризации. и направление распространения (в рассматриваемом случае - пл. xoz), называется плоскостью поляризации.
В общем случае волну можно рассматривать как суперпозицию двух плоских линейно поляризованных волн с взаимно перпендикулярной ориентацией векторов , распространяющихся в одном (вдоль z) направлении. , распространяющихся в одном (вдоль z) направлении.
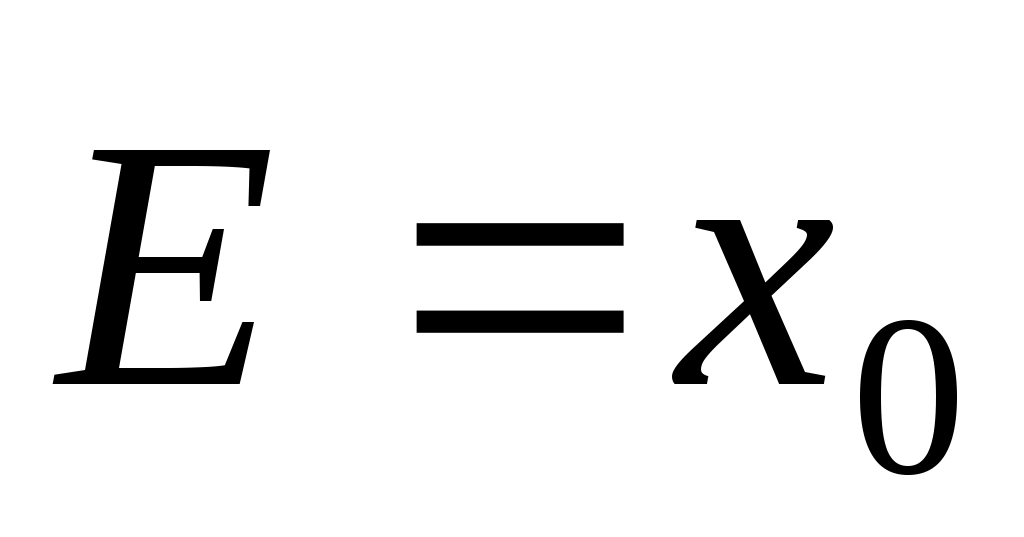 Emx cos ( t – kz + 1) + Emx cos ( t – kz + 1) + 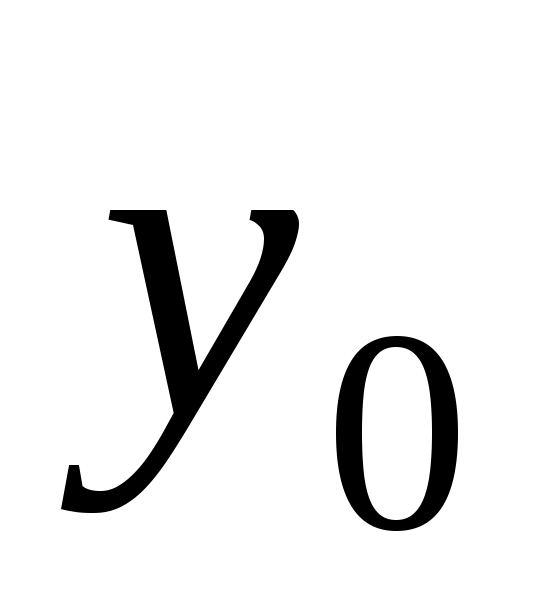 Emy cos ( t – kz + 2), Emy cos ( t – kz + 2),
где Emx, Emy –амплитуды составляющих Еx и Ey соответственно, 1 и 2 – фазы этих составляющих в точке z = 0 при t= 0.
Характер изменения вектора  волны с течением времени в фиксированной точке пространства зависит от соотношения между начальными фазами 1 , 2 и от амплитуд Emx, Emy. В общем случае угол может меняться со временем. волны с течением времени в фиксированной точке пространства зависит от соотношения между начальными фазами 1 , 2 и от амплитуд Emx, Emy. В общем случае угол может меняться со временем.
1. Если 1 = 2, вектор  в любой момент времени лежит в плоскости, проходящей через ось z и составляющей угол = arctg (Emy / Emx) c плоскостью xoz. С течением времени конец вектора в любой момент времени лежит в плоскости, проходящей через ось z и составляющей угол = arctg (Emy / Emx) c плоскостью xoz. С течением времени конец вектора  перемещается вдоль отрезка прямой, составляющей с осью x угол θ. Волна является линейно поляризованной. перемещается вдоль отрезка прямой, составляющей с осью x угол θ. Волна является линейно поляризованной.
2. Если амплитуды волн Emx = Emy= Е0, а фазы отличаются на . Тогда
= t – kz + 1 + m,m – целое - в фиксированной точке пространства угол увеличивается пропорционально t. Величина модуля вектора  при этом остается неизменной. при этом остается неизменной.  = E0. Конец вектора описывает окружность – это волна круговой поляризации. Если вектор = E0. Конец вектора описывает окружность – это волна круговой поляризации. Если вектор  вращается по часовой стрелке (если смотреть вдоль направления распространения) (1 - 2 = ), то это правая круговая поляризация. При вращении вектора против часовой стрелки – левая круговая поляризация. Вектор вращается по часовой стрелке (если смотреть вдоль направления распространения) (1 - 2 = ), то это правая круговая поляризация. При вращении вектора против часовой стрелки – левая круговая поляризация. Вектор  вращается в направлении от опережающей по фазе составляющей вектора к отстающей. вращается в направлении от опережающей по фазе составляющей вектора к отстающей.
Волну с линейной поляризацией можно представить как суперпозицию двух волн круговой поляризации, имеющих одинаковые амплитуды и противоположные направления вращения.
3. В общем случае амплитуда и направление вектора  не остаются постоянными. Вектор не остаются постоянными. Вектор , вращаясь в плоскости z = const, изменяет свою длину так, что его конец описывает эллипс. Это волна эллиптической поляризации. , вращаясь в плоскости z = const, изменяет свою длину так, что его конец описывает эллипс. Это волна эллиптической поляризации.
Заметим, что направление вектора  меняется в пространстве и во времени также как и направление вектора меняется в пространстве и во времени также как и направление вектора , поскольку пространственный угол между ними составляет 900, а фазовые углы равны (в среде без потерь). , поскольку пространственный угол между ними составляет 900, а фазовые углы равны (в среде без потерь).
Волновые явления на границе двух сред
В общем случае направление распространение волны можно охарактеризовать волновым комплексным вектором 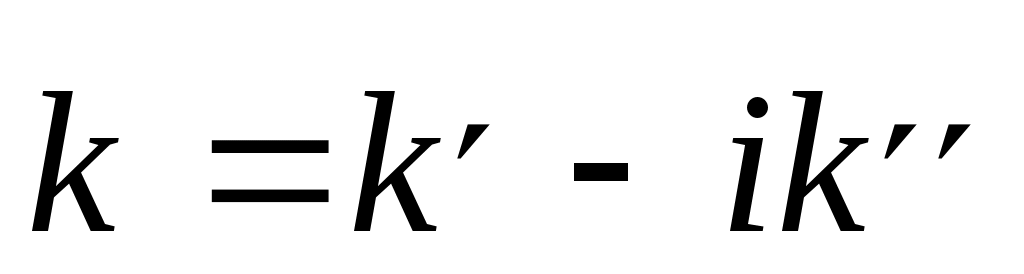 . При этом поле падающей волны описывается выражением . При этом поле падающей волны описывается выражением
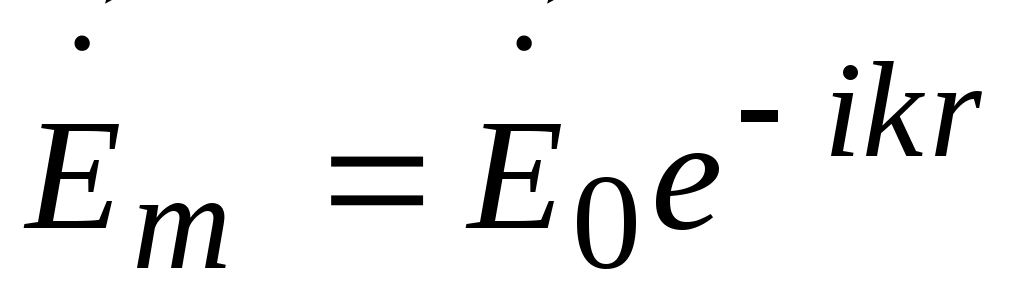 , , 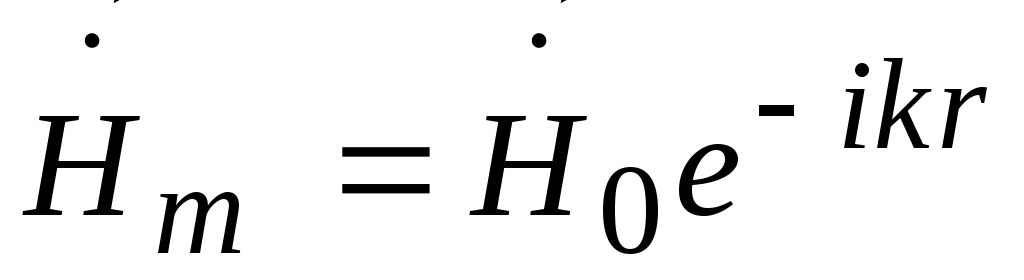 , ,
где 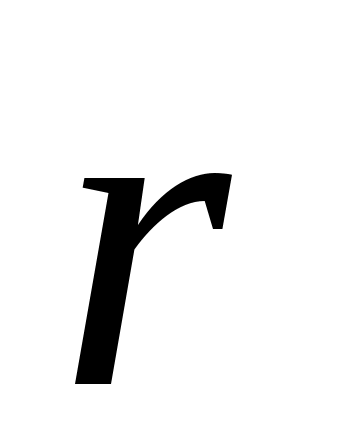 – радиус – вектор, определяющий положение в пространстве исследуемой точки. – радиус – вектор, определяющий положение в пространстве исследуемой точки.
Пусть две однородные изотропные среды, из которых первая характеризуется параметрами r1, r1, а вторая r2, r2, разделены плоской границей. В первой среде под углом от нормали к границе раздела распространяется плоская однородная волна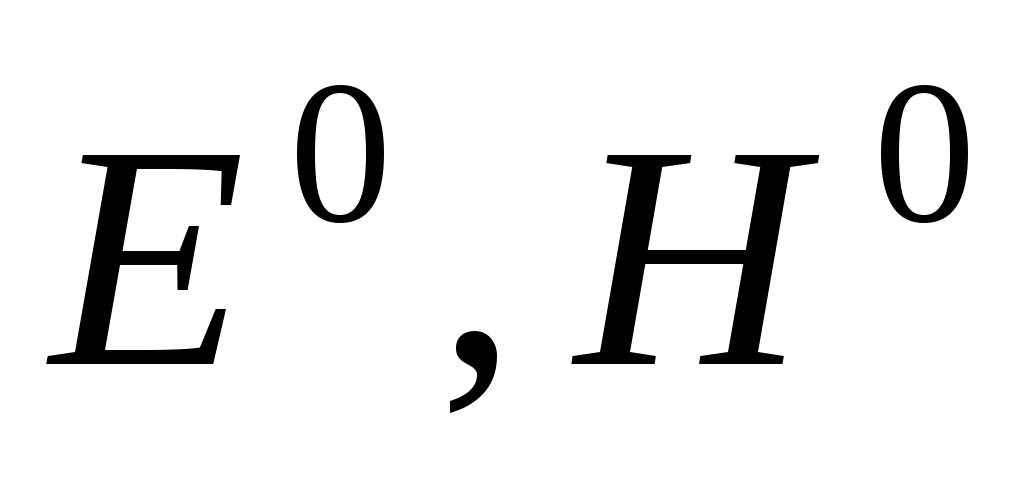 - падающая волна. Угол – это угол падения. Плоскость, проведенная через нормаль к поверхности раздела и направление распространения волны, называется плоскостью падения. В первой среде возникает отраженная волна - падающая волна. Угол – это угол падения. Плоскость, проведенная через нормаль к поверхности раздела и направление распространения волны, называется плоскостью падения. В первой среде возникает отраженная волна  , и во второй – прошедшая или преломленная волна , и во второй – прошедшая или преломленная волна 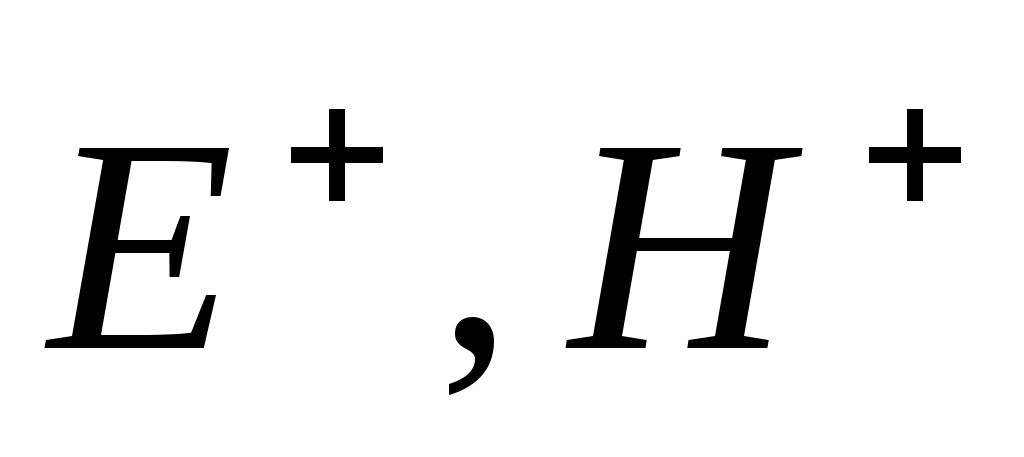 . Угол ’, образованный направлением распространения отраженной волны и направлением нормали к плоскости раздела, называется углом отражения, угол, образованный направлением распространения преломленной волны и нормалью, - углом преломления . . Угол ’, образованный направлением распространения отраженной волны и направлением нормали к плоскости раздела, называется углом отражения, угол, образованный направлением распространения преломленной волны и нормалью, - углом преломления .
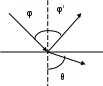
В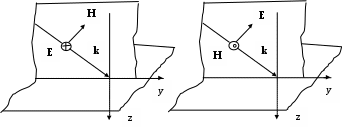 ектор ектор 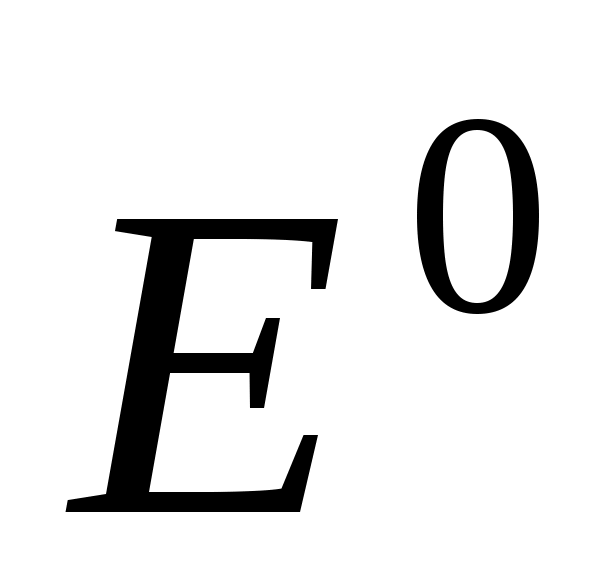 падающей волны (говорим о линейно поляризованных волнах) перпендикулярен направлению распространения. Обычно ограничиваются рассмотрением случая горизонтальной и вертикальной поляризации. Все другие случаи можно представить как суперпозицию этих двух. Если вектор падающей волны (говорим о линейно поляризованных волнах) перпендикулярен направлению распространения. Обычно ограничиваются рассмотрением случая горизонтальной и вертикальной поляризации. Все другие случаи можно представить как суперпозицию этих двух. Если вектор  параллелен плоскости раздела, то поляризация называется горизонтальной. При этом вектор параллелен плоскости раздела, то поляризация называется горизонтальной. При этом вектор  лежит в плоскости падения. Если вектор лежит в плоскости падения. Если вектор  лежит в плоскости падения, а вектор лежит в плоскости падения, а вектор  параллелен плоскости раздела, то поляризация называется вертикальной. параллелен плоскости раздела, то поляризация называется вертикальной.
Горизонтальная () поляризация Вертикальная (||) поляризация
Угол падения волны φ, угол отражения φ’ и угол преломления θ связаны законами Снелиуса.
=’ – угол падения равен углу отражения. Это первый закон Снелиуса.
sin sin = k1 k2 =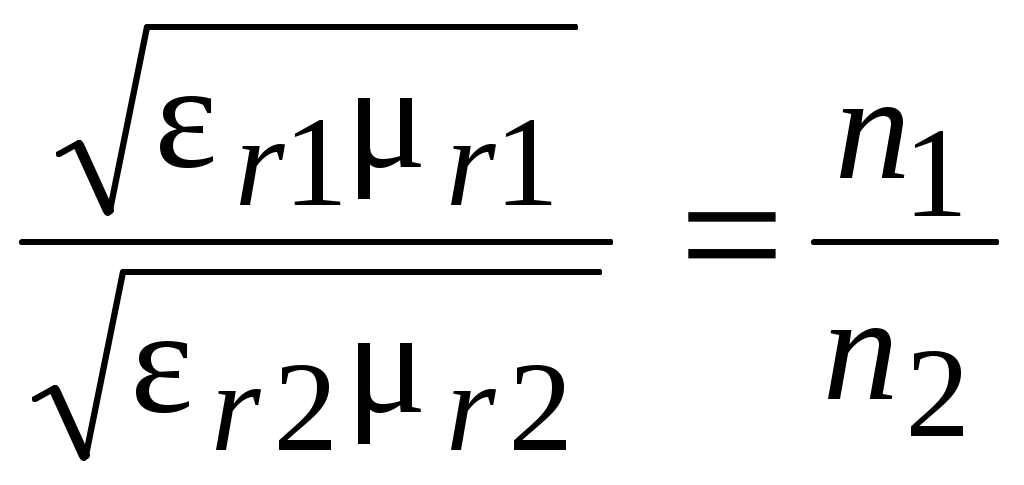 - второй закон Снелиуса. - второй закон Снелиуса.
n1,n2–коэффициенты преломления сред. 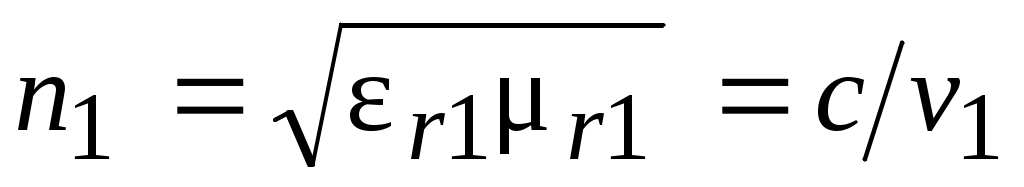 , , 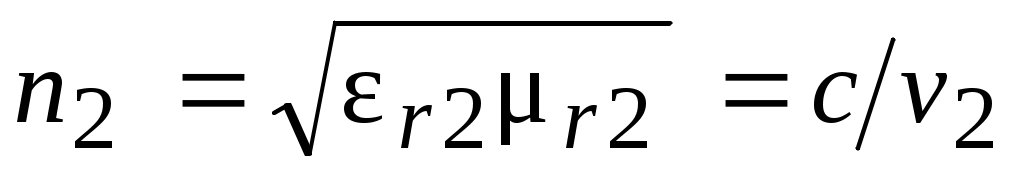
v1, v2 – фазовые скорости волны в среде. sin sin = v2 v1.
Если первая среда оптически долее плотная. n1 > n2, то при некотором угле
= ( - предельный угол внутреннего отражения), .
sin = k2 / k1 = n2 / n1.
Комплексные амплитуды поля отраженной и прошедшей волн (при заданной падающей волне) должны зависеть от поляризации падающей волны.
По определению R 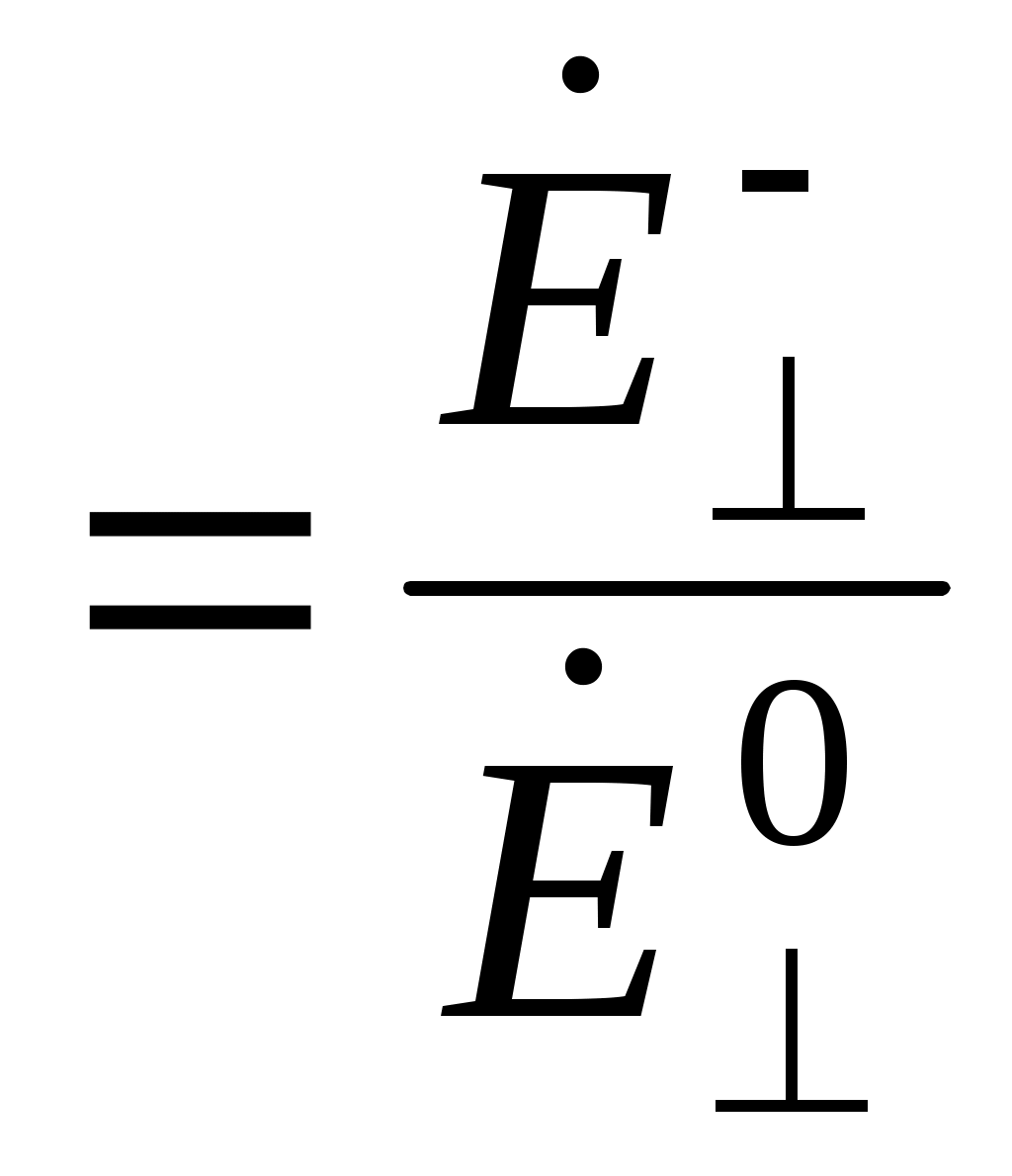 , Т = , Т = 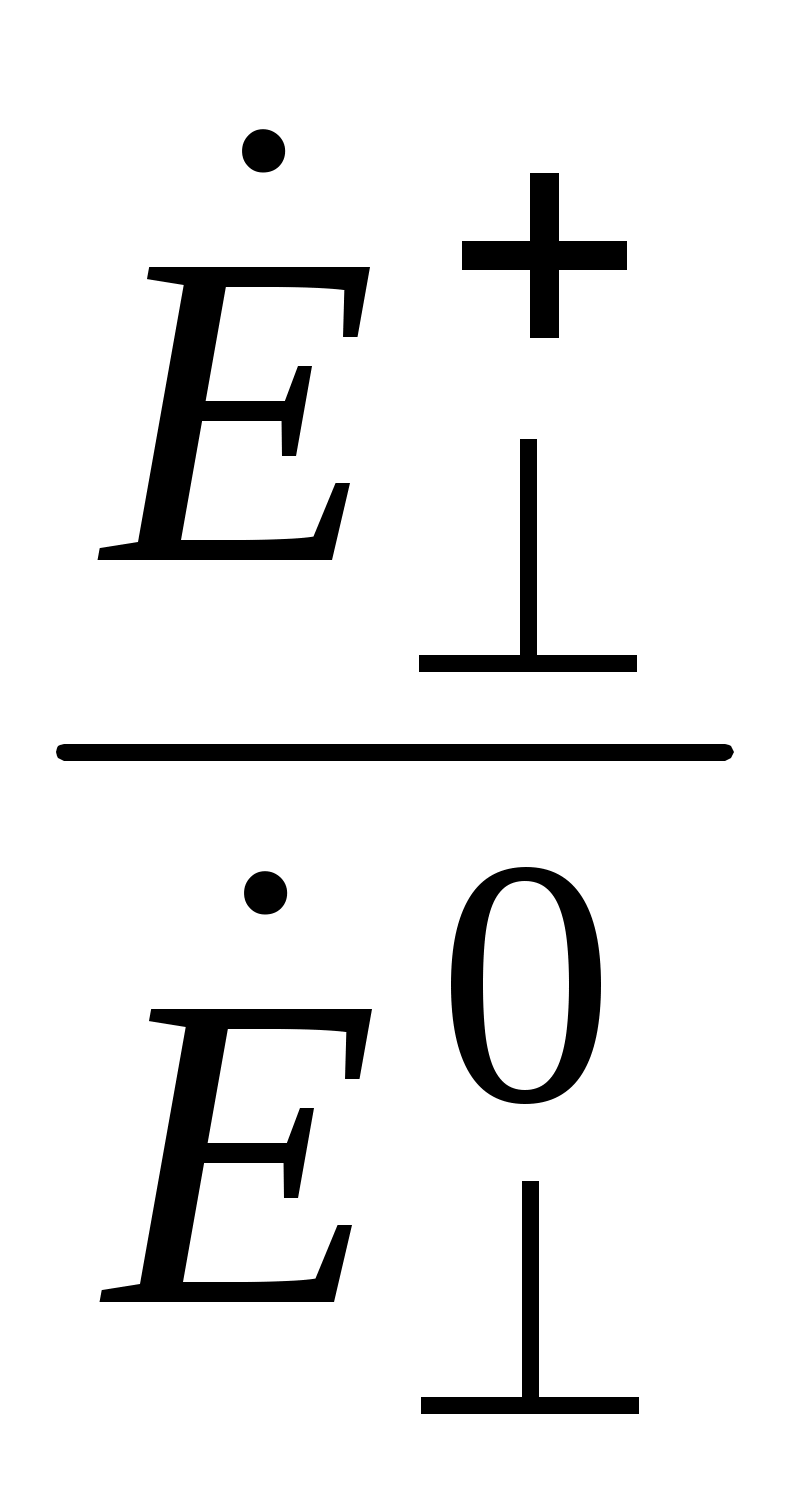
R - коэффициент отражения нормально поляризованной волны (горизонтальная поляризация), Т - коэффициент прохождения нормально поляризованной волны.
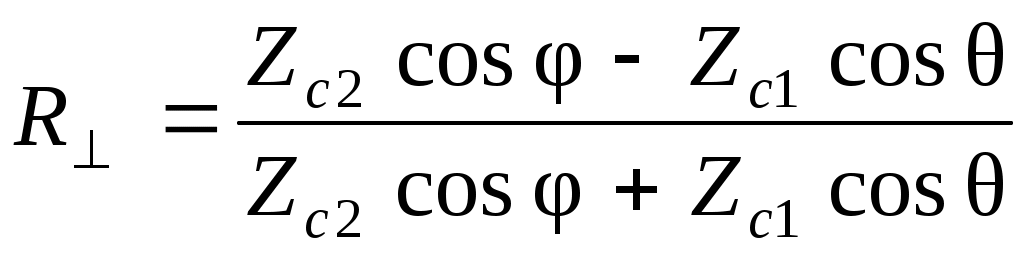 , , 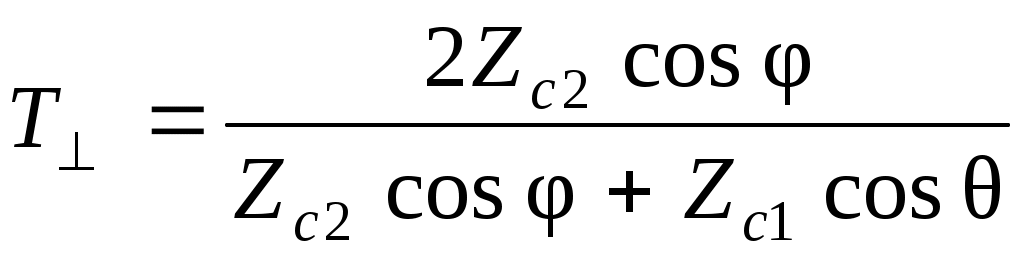 . .
Коэффициенты отражения и прохождения в случае параллельно поляризованной волны (вертикальная поляризация) R=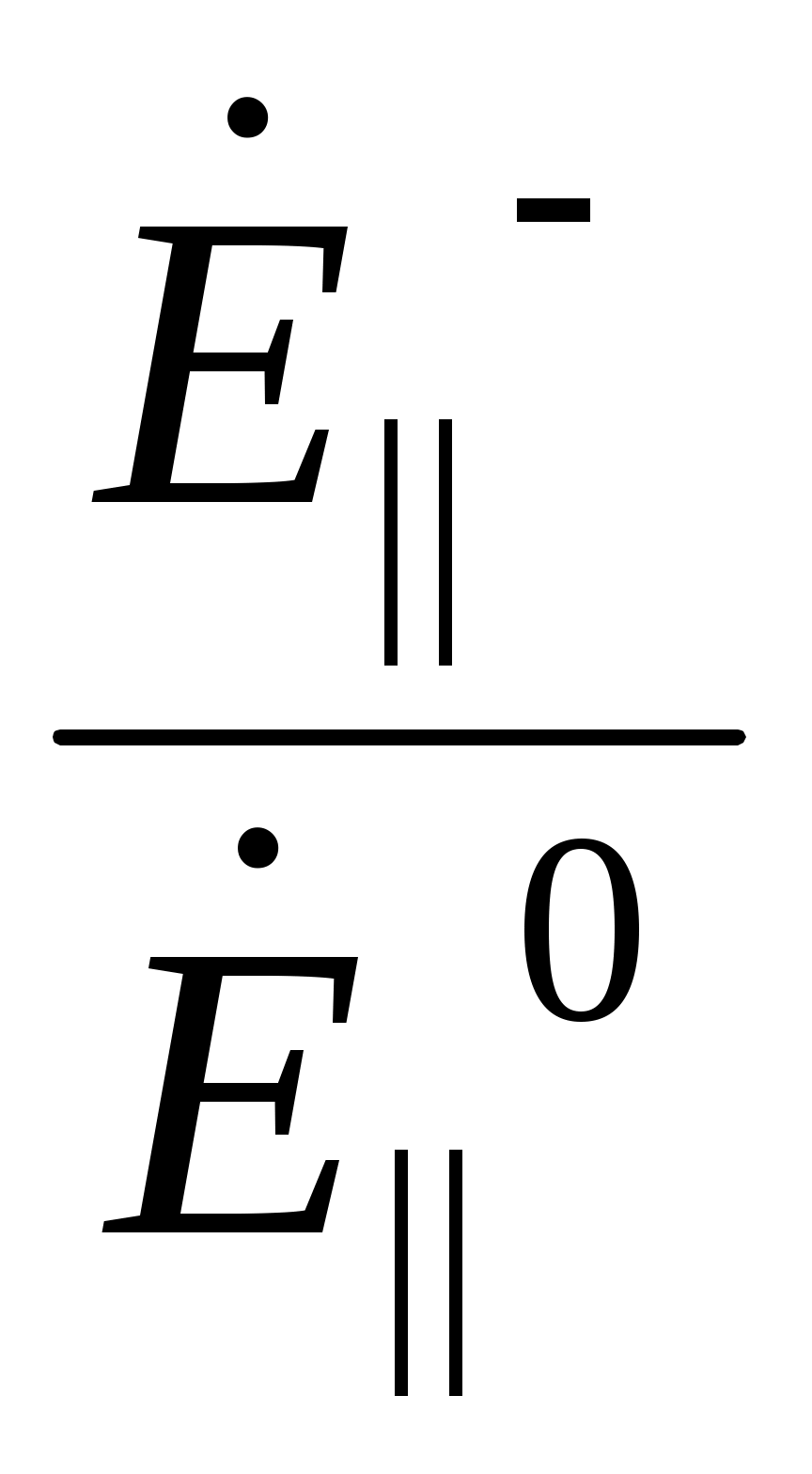 , Т= , Т=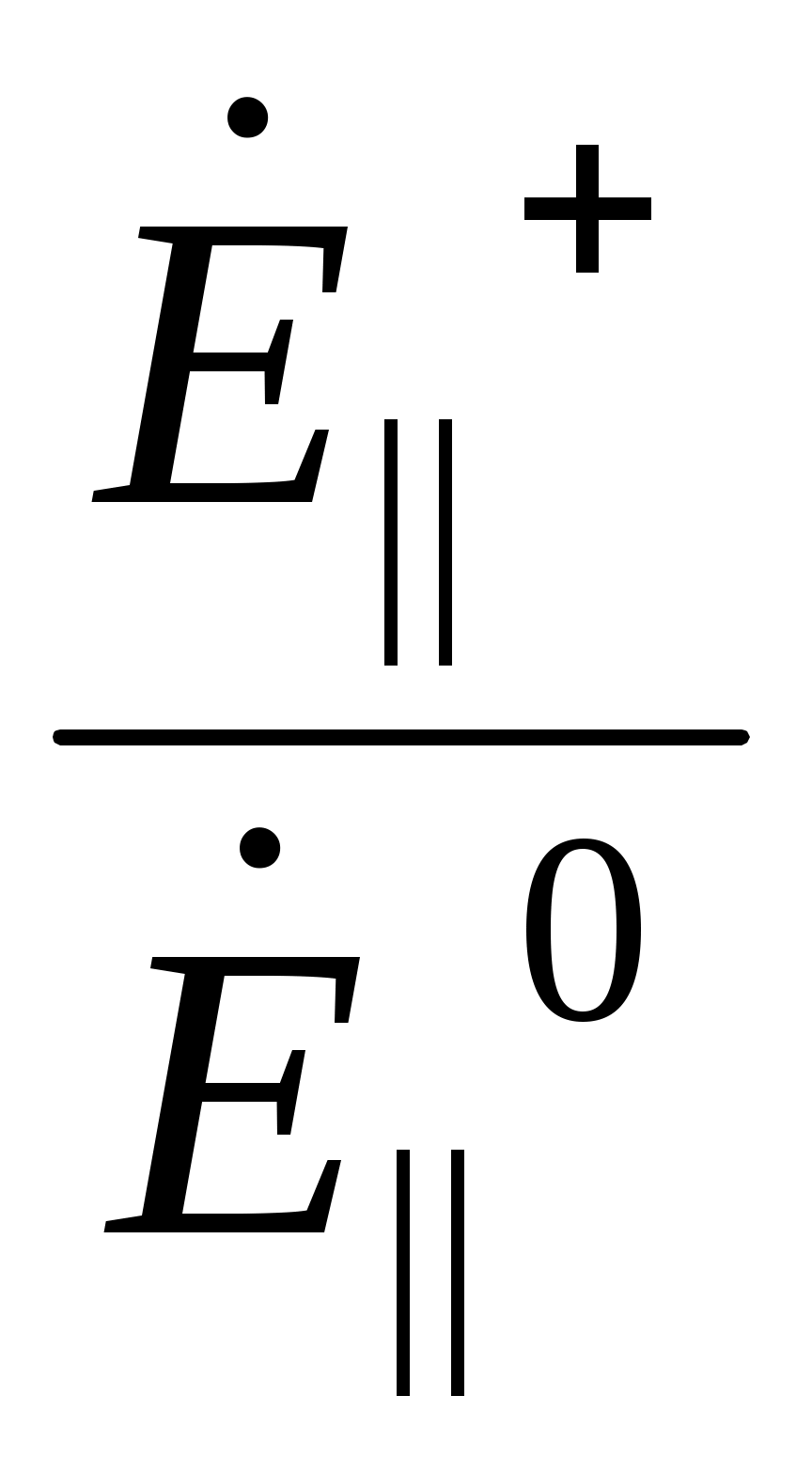
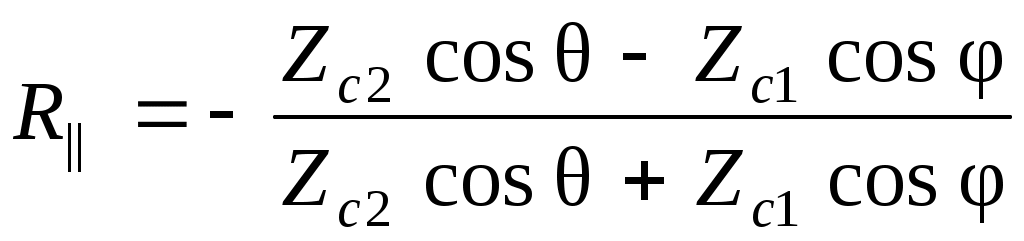 , , 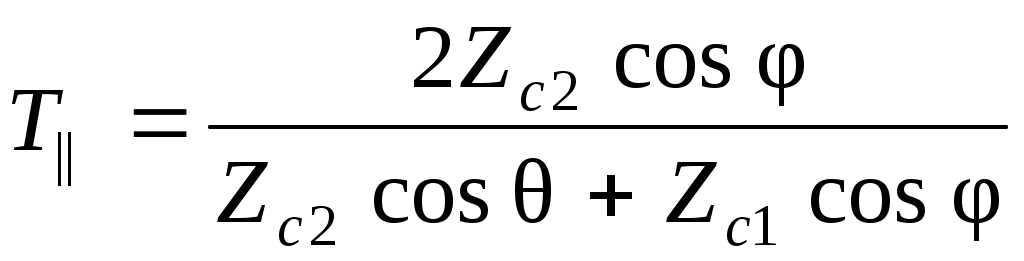
Это формулы Френеля.
Zc1,2 – характеристические сопротивления волны (волновые сопротивления) в среде 1 и 2. 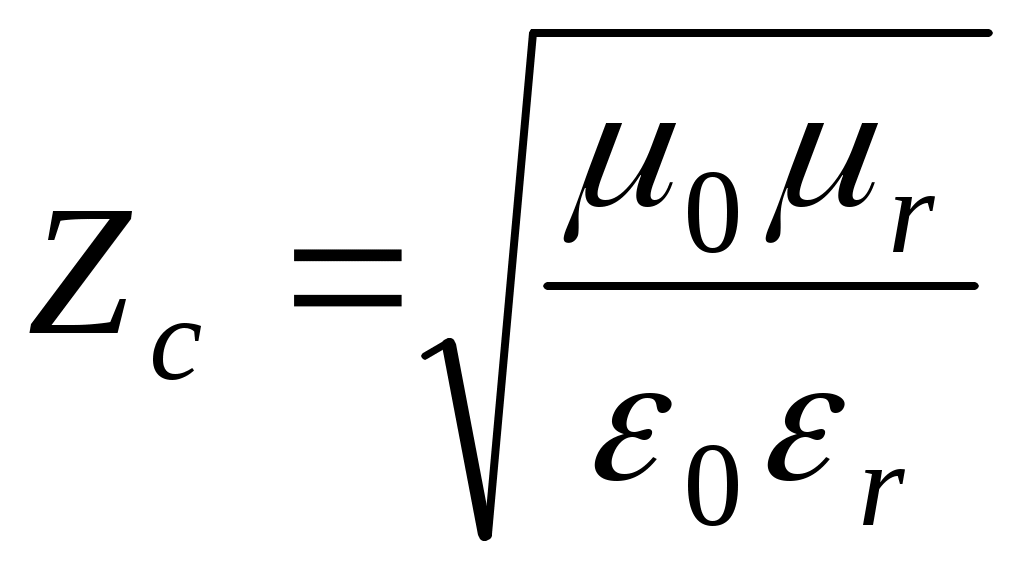
При определенном угле падения Б параллельно поляризованной волны коэффициент отражения R обращается в 0. R = 0 при φ = φБ
Для r2 = r1 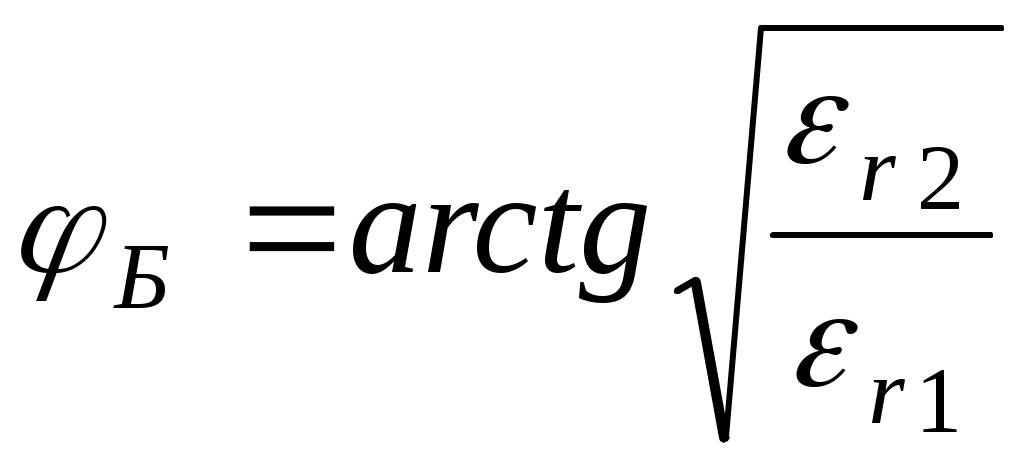 . Б – угол Брюстера – угол полного прохождения параллельно поляризованной волны. . Б – угол Брюстера – угол полного прохождения параллельно поляризованной волны.
Рассмотрим несколько примеров.
а). Предположим, что на границу раздела сред под углом Брюстера падает линейно поляризованная волна. Плоскость поляризации волны составляет угол с плоскостью падения. Какова поляризация отраженной и преломленной волн? В рассматриваемом случае падающая волна имеет составляющие с горизонтальной и вертикальной поляризацией. Следовательно, отраженная волна содержит только составляющую с горизонтальной поляризацией, а составляющая с вертикальной поляризацией проходит через границу раздела сред.
б). Волна круговой поляризации падает на границу раздела сред. Какова поляризация отраженной и преломленной волн?
Плоскую волну круговой поляризации можно представить в виде суперпозиции двух линейно поляризованных волн, в частности волн с горизонтальной и вертикальной поляризациями. Следовательно, волна круговой поляризации будут отражаться при любых углах падения. Соотношение между амплитудами волн с горизонтальной и вертикальной поляризациями в отраженных и преломленных волнах будет иным, чем в падающей волне. Значит, эти волны будут иметь эллиптическую поляризацию. Если плоская волна с круговой поляризацией падает под углом Брюстера, то отраженная волна оказывается линейно поляризованной, а преломленная – эллиптически поляризованной волной. Если верхняя среда оптически более плотная, то при углах падения, превышающих угол полного внутреннего отражения φ*, преломленной волны не будет.
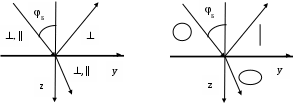
|
|
|
 Скачать 1.51 Mb.
Скачать 1.51 Mb.