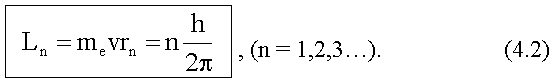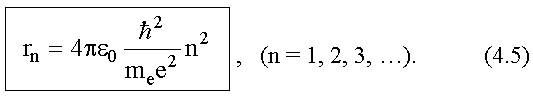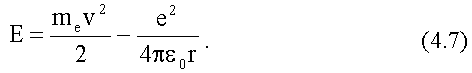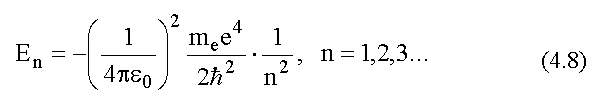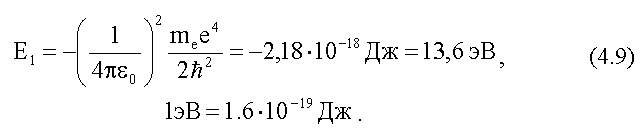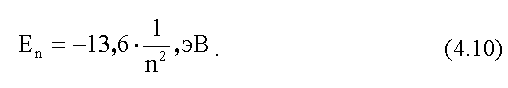ВСЯ ФИЗИКА. Электромагнитная природа света
 Скачать 1.05 Mb.
|
распространяющуюся в том же направлении (например в направлении оси х), в котором движется частица (рис. 3.1). 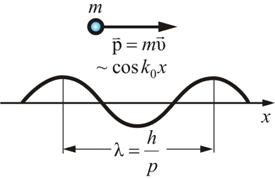 Рис. 3.1 Зависимость волновой функции от координаты х даётся формулой
где – волновое число,аволновой вектор направлен в сторону распространения волны или вдоль движения частицы:
Таким образом, волновой вектор монохроматической волны, связанной со свободно движущейся микрочастицей, пропорционален её импульсу или обратно пропорционален длине волны. Поскольку кинетическая энергия сравнительно медленно движущейся частицы , то длину волны можно выразить и через энергию:
При взаимодействии частицы с некоторым объектом – с кристаллом, молекулой и т.п. – её энергия меняется: к ней добавляется потенциальная энергия этого взаимодействия, что приводит к изменению движения частицы. Соответственно, меняется характер распространения связанной с частицей волны, причём это происходит согласно принципам, общим для всех волновых явлений. Поэтому основные геометрические закономерности дифракции частиц ничем не отличаются от закономерностей дифракции любых волн. Общим условием дифракции волн любой природы является соизмеримость длины падающей волны λ с расстоянием d между рассеивающими центрами: . Длина волны де Бройля — длина волны, которая проявляется у всех частиц в квантовой механике согласно корпускулярно-волновому дуализму, и определяющая плотность вероятности обнаружения объекта в заданной точке конфигурационного пространства. Длина волны де Бройля обратно пропорциональна импульсу частицы. 60) В 1924 г. де Бройль выдвинул гипотезу (предположение), что дуализм (двойственность) не являются особенностью одних только оптических явлений (см. лекцию 8), а имеет универсальное значение, т.е. де Бройль выдвинул гипотезу о всеобщности корпускулярно-волнового дуализма. Согласно де Бройлю каждой частице, независимо от ее природы, следует поставить в соответствии волну, длина которой l связана с импульсом частицы соотношением (формула де Бройля)  , (1)а частота v=E/h или w=2pv=E/  , (2)т.е. определяется энергией Е частицы. Найдем длину волны де Бройля, соответствующую движущемуся электрону. Кинетическая энергия, приобретенная электроном в ускоряющем поле равна  (3)и скорость  (4)Из (1) и (4) следует (учитывая, что е=1.6×10-19 Кл, m=9.1×10-31 кг, напряжение U выражается в вольтах)  . (5)В обычных электронных приборах используют напряжение 1¸104В. Соответствующие длины волн летящих электронов составляют 10¸0.1  , т.е. изменяются в диапазоне длин волн обычных рентгеновских лучей (см. параграф 2.5).По гипотезе де Бройля не только фотоны , но и все «обыкновенные частицы» (электроны, протоны, нейтроны и др.) обладают волновыми свойствами, которые, в частности, должны проявляться в явлениях интерференции, дифракции. | |
. Наряду с частотой, спектральная линия характеризуется волновым числом (с - скорость света) и длиной волны 
. Частоты спектральных линий выражают в с-1, волновые числа - в см-1, длины волн - в нм и мкм, а также в ангстремах ( ). В спектроскопии волновые числа также обозначают буквой .Для данного элемента могут наблюдаться спектральные линии нейтрального атома и спектральные линии ионизованного атома. Линии спектра нейтрального атома принято отмечать цифрой I при символе хим. элемента, линии, принадлежащие положит. ионам,- римскими цифрами II, III, ... соотв. кратности иона (напр., NaI, NaII, NaIII,... для Na, Na+ , Na++, ...), при этом часто говорят о 1-м, 2-м, 3-м ... спектре данного элемента.
Наиболее простыми атомными спектрами обладают атом водорода и водородоподобные ионы (спектры HI, HeII, LiIII, . . .), к-рые состоят из закономерно расположенных спектральных линий, образующих спектральные серии.
Волновые числа для спектральных линий серии атома водорода и водородоподобных атомов определяются ф-лой
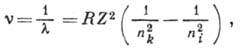
где nk и ni - гл. квантовые числа для нижнего и верхнего уровней энергии (см. рис. 1 в ст. Атом R ),- Ридберга постоянная, Z - ат. номер. При nk= 1, 2, 3, 4, 5,6 и ni=nk+l, nk+2, . . . , h для атома водорода (Z=1)получаются соотв. серии Лаймана, Бальмера, Пашена, Брэкета, Пфунда, Хамфри. Для каждой серии существует предел - граница ионизации, соответствующая
, линии серии сходятся к границе ионизации. В лаб. условиях наблюдения спектра водорода (напр., в электрич. разрядах) серия Лаймана получается как в поглощении, так и в испускании. В спектре Солнца наблюдается в поглощении и серия Бальмера (что связано с возбуждением при высоких темп-pax нач. уровня = 2).Спектральные линии атома водорода имеют дублетную тонкую структуру, обусловленную взаимодействием спина электронов с его орбитальным моментом (см. Спин-орбитальное взаимодействие; )величина расщепления линий - порядка десятых долей см-1. Это расщепление для водородоподобных ионов возрастает пропорционально Z4, т. е. для HeII в 16 раз по сравнению с HI.
Сравнительно простыми спектрами обладают атомы щелочных металлов, имеющие один внеш. электрон (одноэлектронные А. с.), их спектральные линии также группируются в серии, волновые числа к-рых выражаются приближённой ф-лой Ридберга:
серия получается при заданном nk и разл. значениях ni; а и b постоянны для данной серии. Разл. серии (гл. серия, диффузная серия, резкая серия и др.) отличаются значениями а и b, зависящими от азимутального квантового числа l. Спектральные линии имеют дублетную тонкую структуру, причём величина расщепления быстро возрастает с увеличением Z (от Li к Cs).
Более сложными А. с. (двухэлектронными спектрами) обладают атомы с двумя внеш. электронами; ещё сложнее спектры атомов с тремя и более внеш. электронами. Особенно сложны спектры элементов, для к-рых происходит достройка внутр. электронных оболочек (d-оболочек переходных элементов и -оболочек у лантаноидов и актиноидов; см. Периодическая система элементов). В сложных спектрах серии уже не удаётся выделить. Спектральные линии образуют группы - мультиплеты. В наиб. сложных А. с. число спектральных линий доходит до многих тысяч. Интерпретация сложных спектров с установлением схемы уровней энергии и квантовых переходов между ними представляет трудную задачу систематики А. с.
Систематика атомных спектров основана на характеристике уровней атома при помощи квантовых чисел и на отбора правилах ,определяющих, какие из квантовых переходов возможны. При наличии одного внеш. электрона уровни энергии атома характеризуются (помимо гл. квантового числа электрона) его квантовыми числами l, s и j, определяющими величины орбитального момента , спинового момента и полного момента
. Согласно правилам отбора 
, = 0 1. Для атомов с двумя или неск. внеш. электронами характеристика уровней энергии более сложна и может быть произведена исходя из приближённой характеристики одноэлектронных состояний при помощи квантовых чисел пi , li и si (li = 0, 1, 2, ..., ni = 1, 
I и применяя векторную схему сложения орбитальных моментов 
и спиновых моментов
.В случае нормальной связи, когда электростатич. взаимодействия электронов много больше их магн. взаимодействий, что чаще всего имеет место, орбитальные моменты отд. электронов
складываются в полный орбитальный момент 
, а их спиновые моменты 
в полный спиновой момент 
; затем сложение 
и 
даёт полный момент атома: 
. Уровни энергии характеризуются значениями квантовых чисел L, S и J, определяющих величины соответствующих моментов. Квантовое число J сохраняет свой смысл и при др. схемах связи, когда в соответствии с величинами взаимодействий моменты следует складывать в др. последовательности [в частности, в случае -связи
; этот случай имеет место, когда магн. взаимодействия много больше электростатических]. J определяет величину полного момента атома независимо от схемы связи, и для него имеет место правило отбора
.При нормальной связи квантовое число S, определяющее величину полного спинового момента атома S, принимает целые значения S=0, 1, 2, ..., если атом содержит чётное число электронов, и полуцелые значения
если атом содержит нечётное число электронов. Величина =2S+1 определяет мулътиплетностъ уровней энергии атома и играет важную роль в систематике А. с.Уровни энергии атомов принято обозначать (в случае нормальной связи) символами
, где значения L= 0, 1, 2, 3, 4, 5, 6, 7, ... указываются прописными буквами S, P, D, F, G, H, J, L, ... соответственно. Так, 3D2 обозначает уровень с L = 2, S = 1 ( =2S+ 1 = 3) и J =2; 1S0-уровень с L = 0, S = 0 ( =25 + 1 =0) и J = 0. Нечётные уровни (см. Чётность у ровня)обозначают индексом °, напр. 
(нечётный уровень с L = 1, S = 1/2, J = 1/2).Для более подробной характеристики уровня перед символом
указывают электронную конфигурацию (см. Атом ),напр. для атома Не уровень 3S1, возникающий из конфигурации 1s 2s, обозначается как 
(L = 0, S= s1 + s2 =1, J=1). Для одноэлектронного атома полная запись будет 
и сокращённо пишут просто 
, напр. для осн. уровня атома водорода 
(n = 1, L = 0, S = J = 1/2) вместо 
.52. Сериальные формулы. 53. Опыт Резерфорда.
3) Атомные спектры. Сериальные формулы. Опыты по рассеянию альфа-частиц (опыты Резерфорда).
Атомные спектры, спектры оптические, получающиеся при испускании или поглощении света (электромагнитных волн) свободными или слабо связанными атомами; такими спектрами обладают, в частности, одноатомные газы и пары. А. с. являются линейчатыми — они состоят из отдельных спектральных линий. А. с. наблюдаются в виде ярких цветных линий при свечении газов или паров в электрической дуге или разряде (спектры испускания) и в виде тёмных линий (спектров поглощения). Каждая спектральная линия характеризуется определённой частотой колебаний v испускаемого или поглощаемого света и соответствует определённому квантовому переходу между уровнями энергии Ei и Ek атома согласно соотношению: hv = Ei - Ek, где h — Планка постоянная). Наряду с частотой спектральную линию можно характеризовать длиной волны l = c/v, волновым числом 1/l = v/c (c — скорость света) и энергией фотона hv.
А. с. возникают при переходах между уровнями энергии внешних электронов атома и наблюдаются в видимой, ультрафиолетовой и близкой инфракрасной областях. Такими спектрами обладают как нейтральные, так и ионизованные атомы; их часто называют соответственно дуговыми и искровыми спектрами (нейтральные атомы легко возбуждаются и дают спектры испускания в электрических дугах, а положительные ионы возбуждаются труднее и дают спектры испускания преимущественно в искровых электрических разрядах). Спектры ионизованных атомов смещены по отношению к спектрам нейтральных атомов в область больших частот, т. е. в ультрафиолетовую область. Это смещение тем больше, чем выше кратность ионизации атома — чем больше электронов он потерял. Спектры нейтрального атома и его последовательных ионов обозначают в спектроскопии цифрами I, II, III, ... В реально наблюдаемых спектрах часто присутствуют одновременно линии нейтрального и ионизованных атомов; так говорят, например, о линиях FeI, FeII, FeIII в спектре железа, соответствующих Fe, Fe+, Fe2+.
Линии А. с. образуют закономерные группы, называются спектральными сериями. Промежутки между линиями в серии убывают в сторону коротких длин волн, и линии сходятся к границе серии. Наиболее прост спектр атома водорода. Волновые числа линий его спектра с огромной точностью определяются формулой Бальмера:
1/l = R(1/n21 - 1/n22), где n1 и n2 значения главного квантового числа для уровней энергии, между которыми происходит квантовый переход
Резерфорд предложил применить зондирование атома с помощью ?-частиц, которые возникают при радиоактивном распаде радия и некоторых других элементов. Масса ?-частиц приблизительно в 7300 раз больше массы электрона, а положительный заряд равен удвоенному элементарному заряду. В своих опытах Резерфорд использовал ?-частицы с кинетической энергией около 5 МэВ (скорость таких частиц очень велика – порядка 107 м/с, но она все же значительно меньше скорости света). ?-частицы – это полностью ионизированные атомы гелия. Этими частицами Резерфорд бомбардировал атомы тяжелых элементов (золото, серебро, медь и др.). Электроны, входящие в состав атомов, вследствие малой массы не могут заметно изменить траекторию ?-частицы. Рассеяние, то есть изменение направления движения ?-частиц, может вызвать только тяжелая положительно заряженная часть атома. От радиоактивного источника, заключенного в свинцовый контейнер, ?-частицы направлялись на тонкую металлическую фольгу. Рассеянные частицы попадали на экран, покрытый слоем кристаллов сульфида цинка, способных светиться под ударами быстрых заряженных частиц. Вспышки на экране наблюдались глазом с помощью микроскопа. Было обнаружено, что большинство ?-частиц проходит через тонкий слой металла, практически не испытывая отклонения. Однако небольшая часть частиц отклоняется на значительные углы, превышающие 30°. Очень редкие ?-частицы (приблизительно одна на десять тысяч) испытывали отклонение на углы, близкие к 180°. Этот результат был совершенно неожиданным даже для Резерфорда. Он находился в резком противоречии с моделью атома Томсона, согласно которой положительный заряд распределен по всему объему атома. При таком распределении положительный заряд не может создать сильное электрическое поле, способное отбросить ?-частицы назад. Резерфорд сделал вывод, что атом почти пустой, и весь его положительный заряд сосредоточен в малом объеме. Эту часть атома Резерфорд назвал атомным ядром. Так возникла ядерная модель атома. Вскоре опираясь на классические представления о движении микрочастиц, Резерфорд предложил планетарную модель атома. Согласно этой модели, в центре атома располагается положительно заряженное ядро, в котором сосредоточена почти вся масса атома. Атом в целом нейтрален. Вокруг ядра, подобно планетам, вращаются под действием кулоновских сил со стороны ядра электроны Находиться в состоянии покоя электроны не могут, так как они упали бы на ядро.
54. Постулаты Бора.(55_)
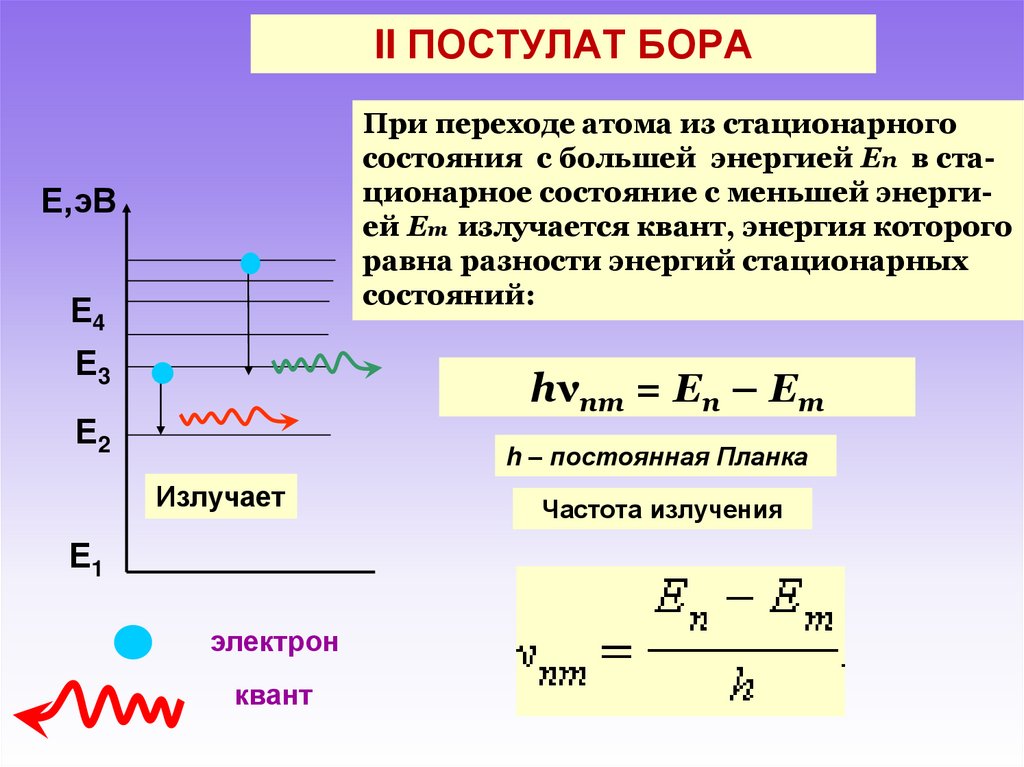
56. Элементарная теория атома водорода.
Боровская теория атома водорода
Атом водорода - простейший из всех атомов. Его ядро - элементарная частица протон. Масса протона в 1836 раз больше массы электрона, вследствие этого ядро в первом приближении можно считать неподвижным и рассматривать только движение электрона (см. рис. 4.1).
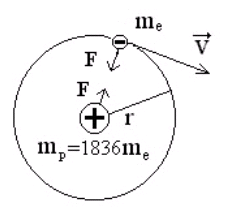
Рис. 4.1.
Заряд протона равен e, онположительный и равен по абсолютной величине заряду электрона, поэтому между ядром и электроном действует кулоновская сила притяжения.
здесь e = 1,6·10-19 Кл - элементарный заряд.
По второму закону Ньютона (см. Ч. 1, (4.4)):
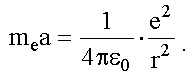
При равномерном движении по окружности радиуса r нормальное ускорение электрона:
После подстановки этого выражения во второй закон Ньютона получим уравнение движения электрона:
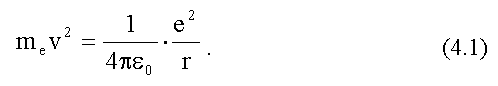
Из этого уравнения не следует никаких ограничений на r - радиус орбиты электрона. Так появилась проблема размера атома: классическая механика позволяла атому иметь любой размер, опыт же показывал, что величина R
