Аррррыфва. Федеральное агентство связи Московский технический университет связи и информатики
 Скачать 290.5 Kb. Скачать 290.5 Kb.
|
|
Федеральное агентство связи Московский технический университет связи и информатики Кафедра теории электрической связи Курсовая работа ПРОЧТИ ПЕРЕД ТЕМ, КАК ПЕЧАТАТЬ!!! Необходимо добавить список литературы, пронумеровать страницы, написать подробное содержание, добавить спектр сигнала на входе дискретизатора. И потом смело сдавай. Студент: Ты прочитал надпись сверху? Вариант: 9 Группа: Факультет: Москва, 2014 г. Исходные данные
Функция корреляции сообщения ВА(τ) = РА(1 + β|τ|)e−β|τ|, β = α·103 РА = β − показатель затухания функции корреляции L − число уровней квантования G0 − постоянная энергетического спектра шума НКС h2 − отношение сигнал-шум по мощности на входе детектора ВА(τ) − функция корреляции сообщения 1. Изобразить структурную схему системы электросвязи и пояснить назначение ее отдельных элементов 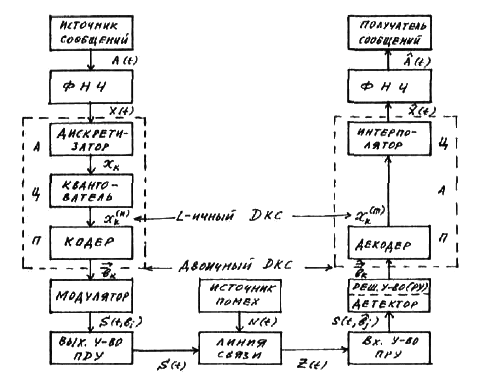 Назначение отдельных элементов схемы: Источник сообщения − это некоторый объект или система, информацию о состоянии которой необходимо передать. ФНЧ − ограничивает спектр сигнала верхней частотой Fв. Дискретизатор − представляет отклик ФНЧ в виде последовательности отсчетов xk. Квантователь − преобразует отсчеты в квантовые уровни Кодер − кодирует квантовые уровни двоичным безызбыточным кодом, т.е. формирует последовательность комбинаций ИКМ Модулятор − формирует сигнал, амплитуда, частота или фаза которого изменяются в соответствии с сигналом Выходное устройство ПДУ − осуществляет фильтрацию и усиление модулированного сигнала для предотвращения внеполосных излучений и обеспечения требуемого соотношения сигнал/шум на входе приемника. Линия связи − среда или технические сооружения по которым сигнал поступает от передатчика к приемнику. В линии связи на сигнал накладывается помеха. Входное устройство ПРУ − осуществляет фильтрацию принятой смеси − сигнала и помехи. Детектор − преобразует принятый сигнал в сигнал ИКМ Декодер − преобразует кодовые комбинации в импульсы. Интерполятор и ФНЧ − восстанавливают непрерывный сигнал из импульсов-отсчетов. Получатель − некоторый объект или система, которому передается информация. 2. По заданной функции корреляции исходного сообщения: а) Рассчитать интервал корреляции, спектр плотности мощности и начальную энергетическую ширину спектра сообщения. Интервал корреляции: 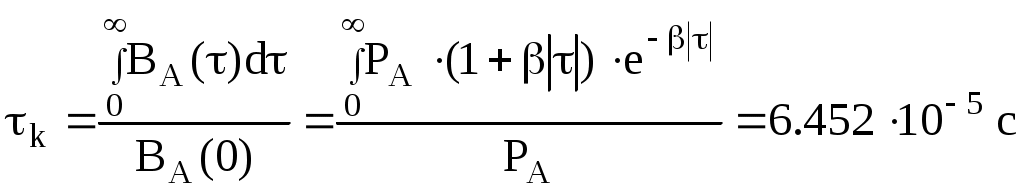 Энергетический спектр (спектр плотности мощности): 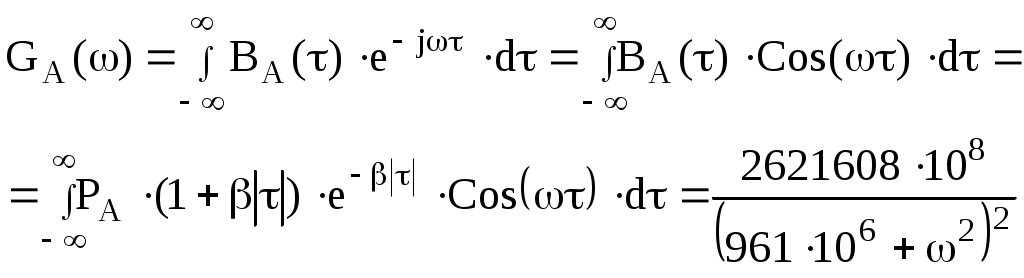 Gmax = GA(0) = 2.839·10−4 В2·с Начальная энергетическая ширина спектра: 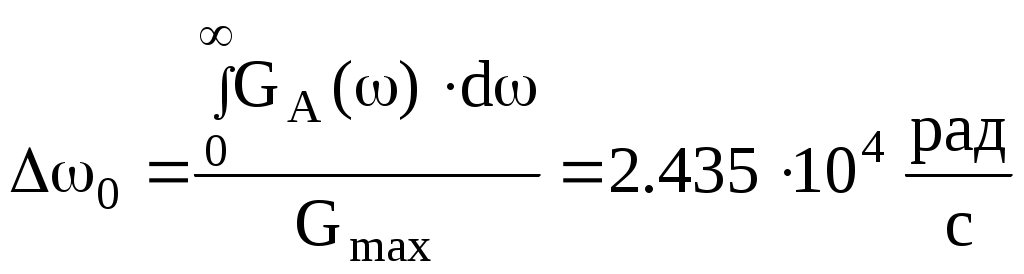 б) Построить в масштабе графики функции корреляции и спектра плотности мощности; отметить на них найденные в п.а) параметры График функции корреляции: 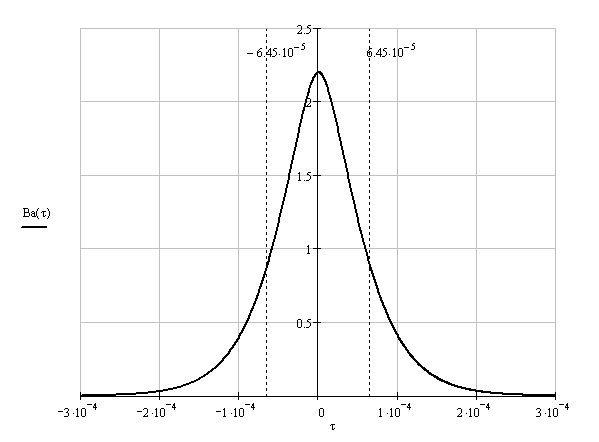 График энергетического спектра: 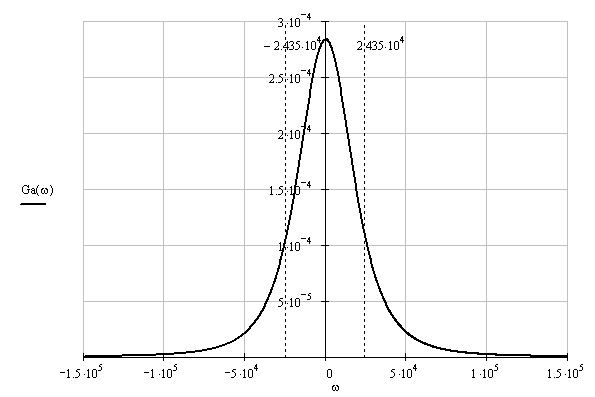 3. Считая, что исходное сообщение воздействует на идеальный фильтр нижних частот (ИФНЧ) с единичным коэффициентом передачи и полосой пропускания, равной начальной энергетической ширине спектра сообщения: а) Рассчитать среднюю квадратическую погрешность фильтрации (СКПФ) сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ. Средняя квадратическая погрешность фильтрации: Мощность отклика ФНЧ: 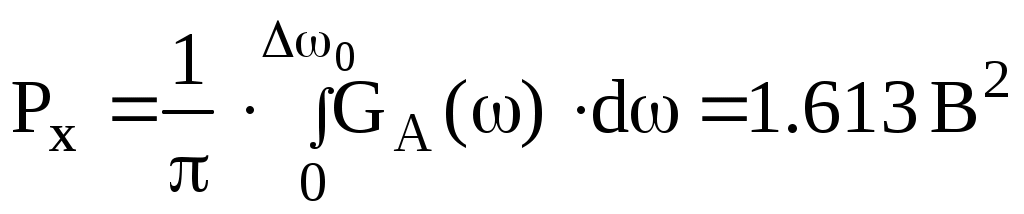 Частота временной дискретизации отклика ИФНЧ: Интервал временной дискретизации отклика ИФНЧ: 4. Полагая, что последовательность дискретных отсчетов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования: а) Рассчитать интервал квантования, пороги и уровни квантования, среднюю квадратическую погрешность квантования (СКПК) Шаг квантования: Пороги квантования:
Уровни квантования: 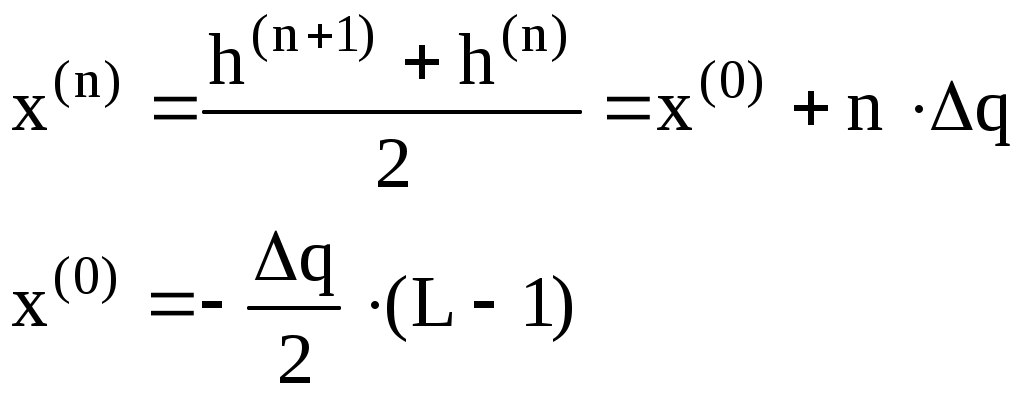
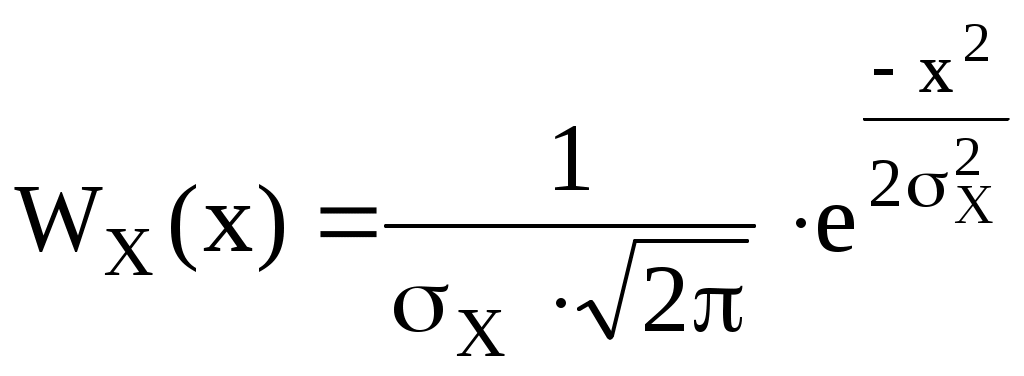 − ФПВ гауссовской случайной величины х − ФПВ гауссовской случайной величины х
KXY = 1 Мощность шума квантования: б) Построить в масштабе характеристику квантования 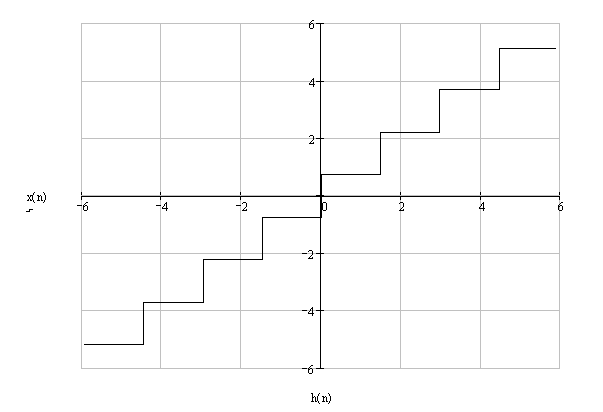 5. Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе L-ичного дискретного канала связи (ДКС): а) Рассчитать закон и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность L-ичного дискретного источника. Распределение вероятностей:
Интегральное распределение вероятностей: Энтропия: Производительность в ДСК: Максимальная энтропия для источника дискретных сообщений: Hmax = log2L = 3 Избыточность последовательности источника: б) Построить в масштабе графики рассчитанных закона и функции распределения вероятностей. График закона распределения вероятности: 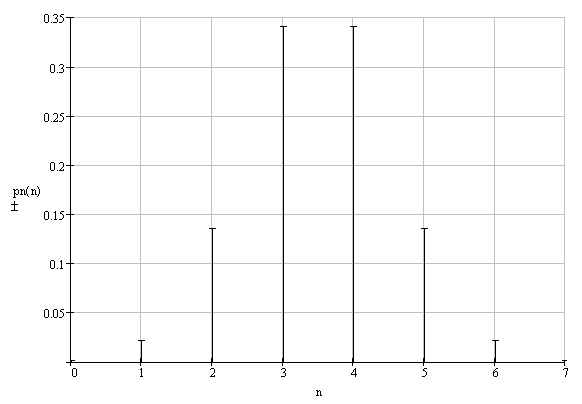 График функции распределения вероятности: 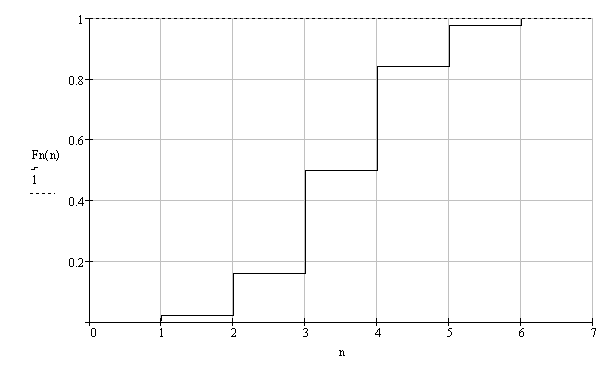 6. Закодировать значения L-ичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации и построить таблицу кодовых расстояний кода. Кодовые комбинации кода: х0 → 0 → 000 x1 → 1 → 001 x2 → 2 → 010 x3 → 3 → 011 x4 → 4 → 100 x5 → 5 → 101 x6 → 6 → 110 x7 → 7 → 111 Таблица кодовых расстояний кода:
а) Рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ. Т.к среднее число нулей Ширина спектра ИКМ сигнала: k1 = 1.667 = const б) Изобразить качественно на одном графике сигналы в четырех сечениях АЦП: вход АЦП, выход дискретизатора, выход квантователя, выход АЦП. Вход АЦП: 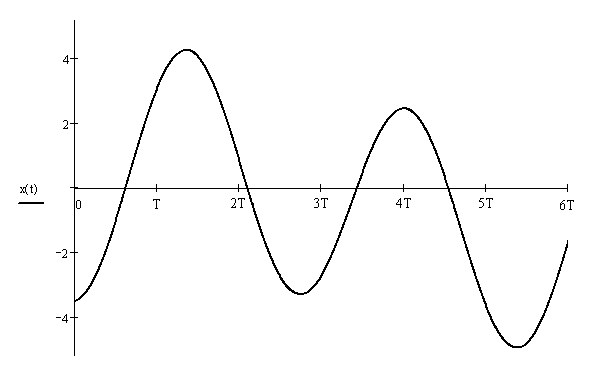 Выход дискретизатора: 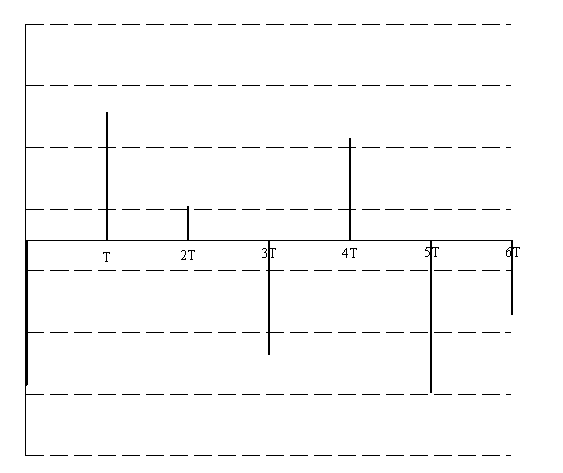 Выход квантователя: 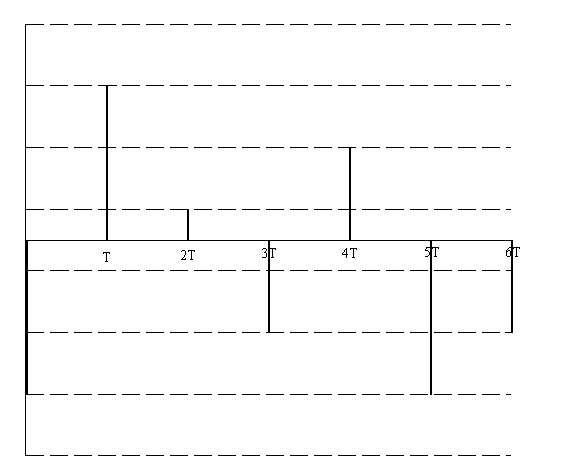 Выход АЦП:  7. Полагая, что для передачи ИКМ сигнала по непрерывному каналу связи (НКС) используется гармонический переносчик: а) Рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра. Спектральное разложение ДОФМ сигнала:
Ширина спектра сигнала ДОФМ: б) Построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нём найденную ширину спектра. 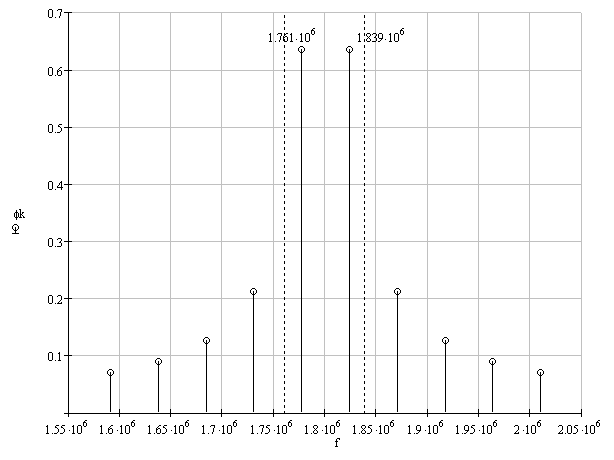 8. Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношением сигнал/шум: а) Рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС. Мощность сигнала ДОФМ: Амплитуда модулированного сигнала: Дисперсия (мощность) аддитивного шума: Пропускная способность НКС: б) Построить в масштабе четыре графика функций плотности вероятностей (ФПВ) мгновенных значений и огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического сигнала с УГП. ФПВ: 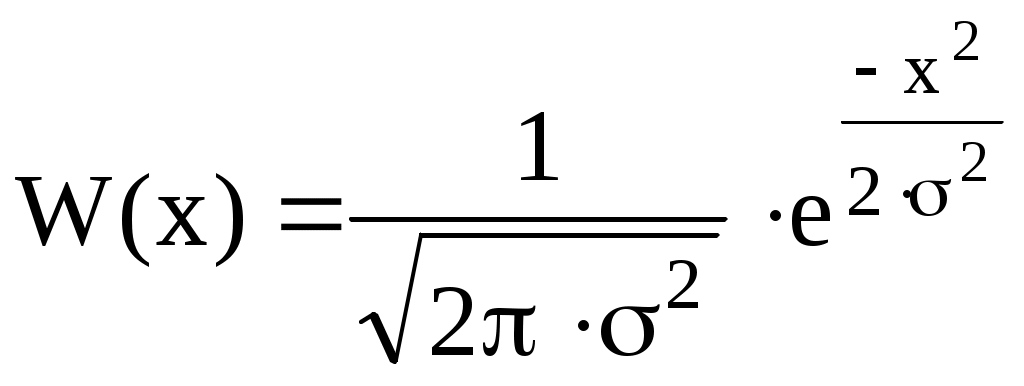 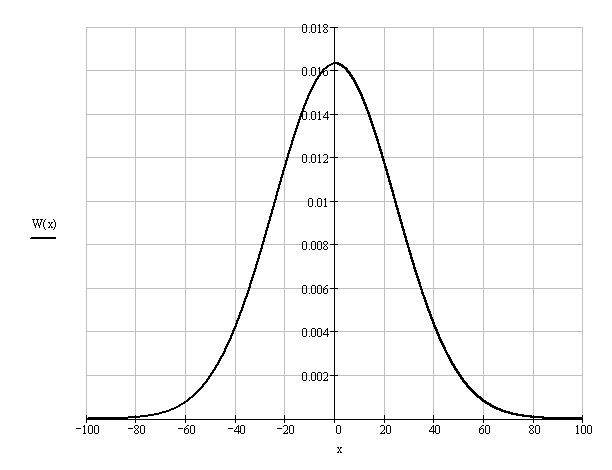 Огибающая гауссовской помехи распределена по закону Релея: 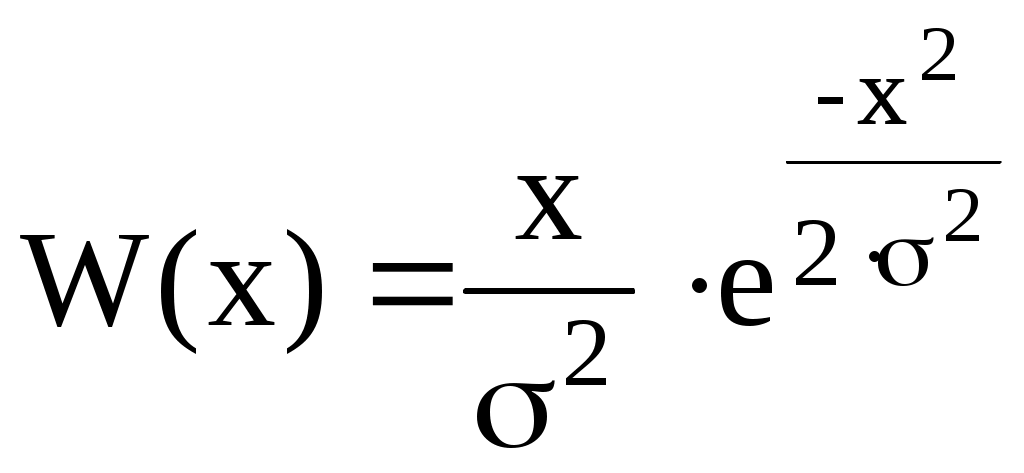 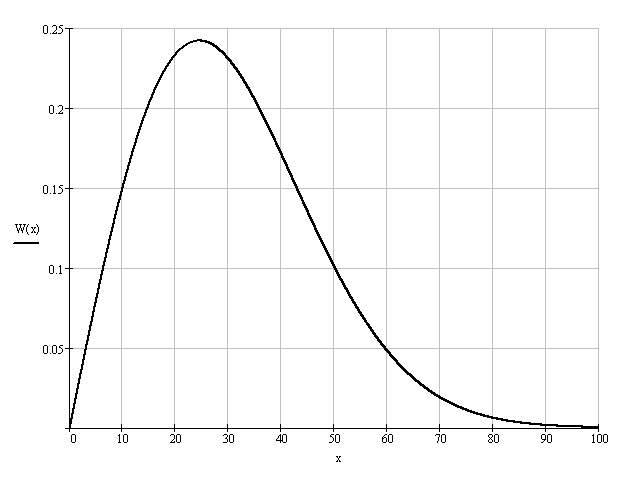 ФПВ аддитивной смеси гармонического сигнала и узкополосной гауссовской помехи: 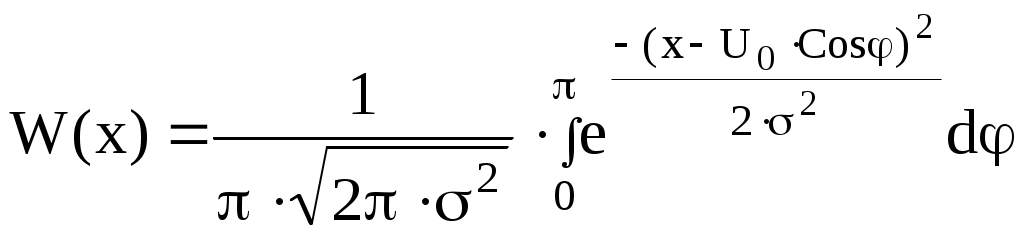 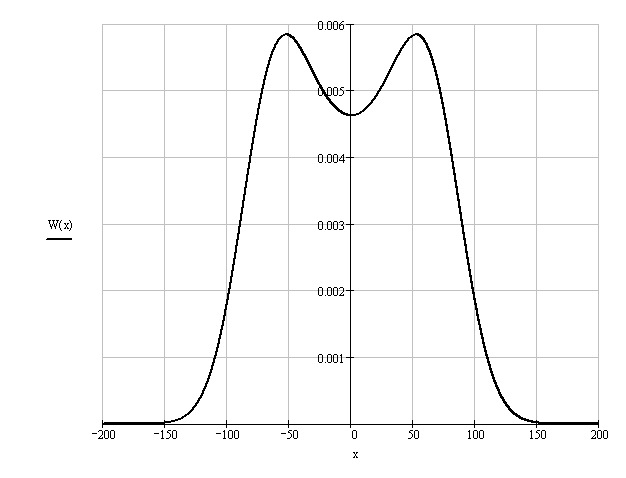 ФПВ огибающей принимаемого сигнала подчиняется обобщенному распределению Рэлея (распределение Райса): 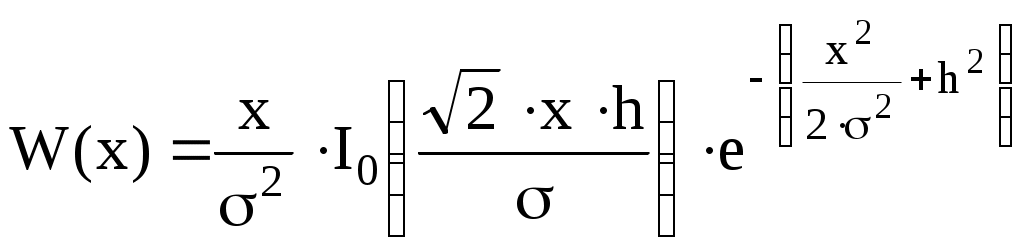 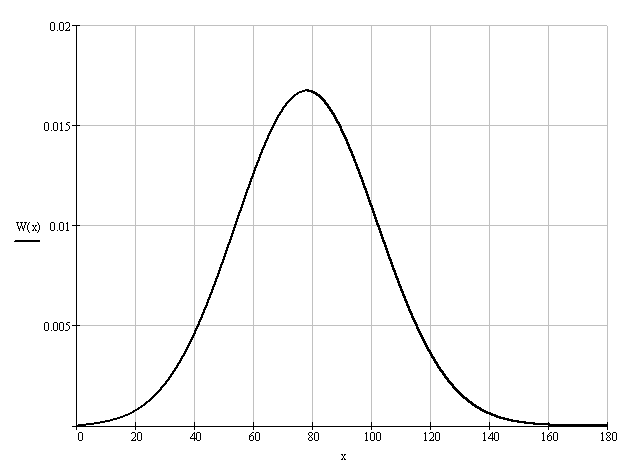 9. С учетом заданного вида приема (детектирования) сигнала дискретной модуляции: а) Рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС. За количественную меру помехоустойчивости в системах электросвязи принимают среднюю на бит вероятность ошибки: Рош.ср = р(0)р(1/0) + р(1)р(0/1) При равенствах априорных вероятностей р(0) = р(1) = 0.5, а также условных вероятностей р(1/0) = р(0/1) = рош (условие симметричности двоичного ДКС), средняя на бит вероятность ошибки равна рош.ср = рош Скорость передачи информации по двоичному симметричному ДКС: 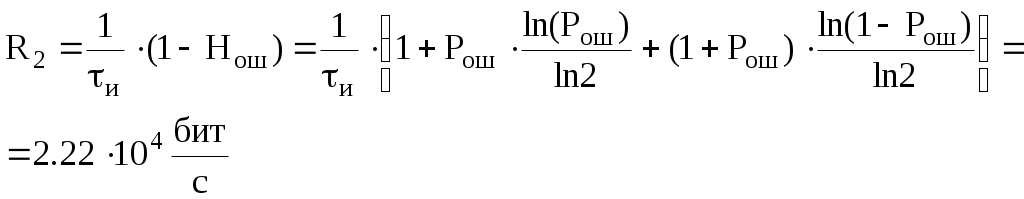 Показатель эффективности: б) Изобразить схему приемника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи, когда он выносит ошибочные решения.   S(t, bi) – сигнал дискретной модуляции S(t, bi) – сигнал дискретной модуляции   + помеха (шум) в НКС + помеха (шум) в НКСПрием сигналов ДОФМ (метод СФ) 1     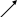       ПФ ПФ f0fS 0 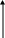 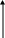 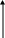  ЛЗ  И И Детектирование сигнала ДОФМ производится двумя методами: методом сравнения фаз и методом сравнения полярностей. При методе сравнения фаз в фазовом детекторе сравниваются фазы текущего и предыдущего, задержанного на время и, колебаний. Под действием помех в канале связи РУ может ошибаться (выносить неправильные решения). Ошибочные решения бывают двух видов: переход 0 в 1 (передавался 0, но РУ выдало решение 1), характеризующийся условной (апостериорной) вероятностью ошибки p(1/0); переход 1 в 0 (передавалась 1, но РУ выдало решение 0), характеризующийся условной вероятностью ошибки p(0/1). 10. Рассматривая отклик декодера ПРУ как случайный дискретный сигнал на выходе L-ичного ДКС: а) Рассчитать распределение вероятностей дискретного сигнала на выходе декодера, скорость передачи информации по L-ичному ДКС, относительные потери в скорости передачи информации по L-ичному ДКС. Распределение вероятностей дискретного сигнала на выходе детектора:
Энтропия ошибочных решений: Энтропия восстановленного L-ичного сигнала: Скорость передачи информации по L-ичному ДКС: Относительные потери в скорости: б) Построить в масштабе график закона распределения вероятностей отклика декодера и сравнить его с законом распределения вероятностей отклика квантователя. 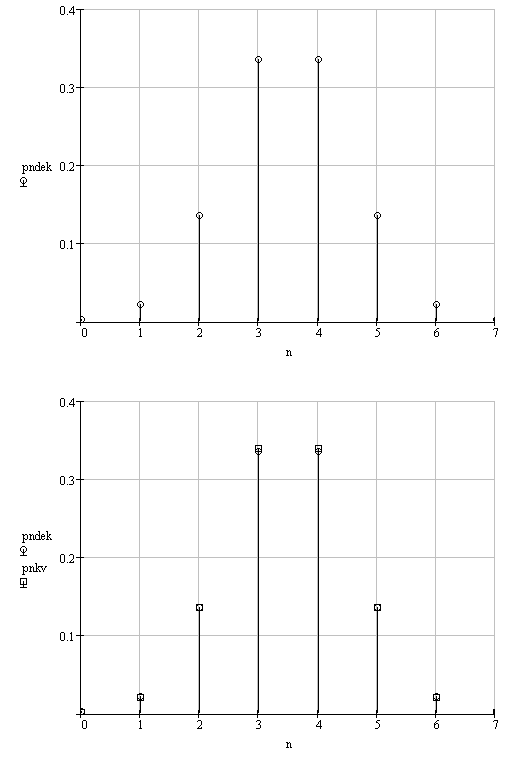 11. Полагая ФНЧ на выходе ЦАП приемника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения: а) Рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, среднюю квадратическую погрешность шума передачи (СКПП), суммарную начальную СКП восстановления непрерывного сообщения (ССКП), относительную СКП (ОСКП). СКПП: 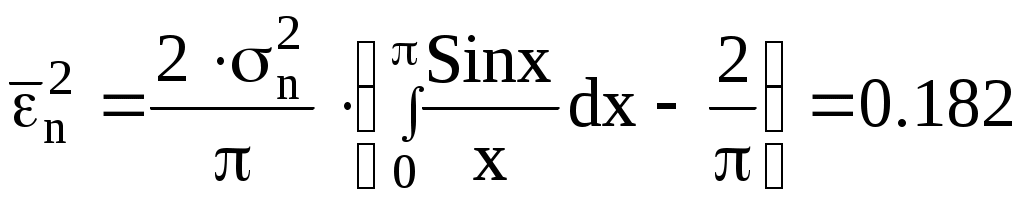 В2 В2ССКП: ОСКП: 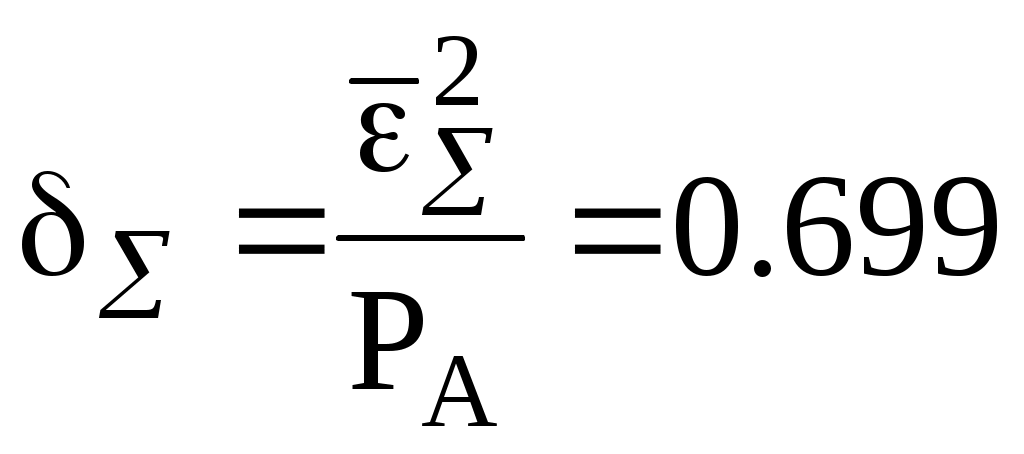 б) Качественно изобразить сигналы на выходе декодера и интерполятора ЦАП, а также восстановленного сообщения на выходе системы электросвязи. 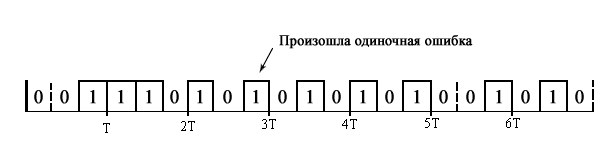 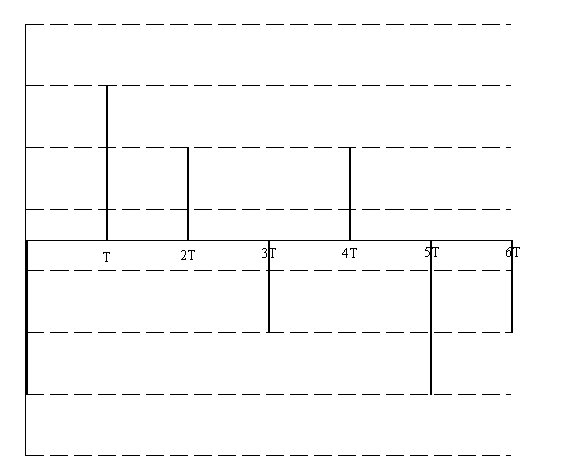 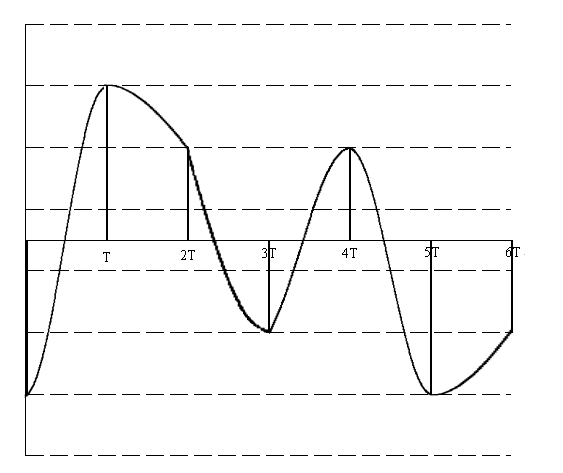 12. В виду того, что выбор начальной энергетической ширины спектра исходного сообщения не приводит к минимуму ОСКП, решить оптимизационную задачу: с помощью ЭВМ определить оптимальную энергетическую ширину спектра сообщения, доставляющую минимум относительной суммарной СКП его восстановления. 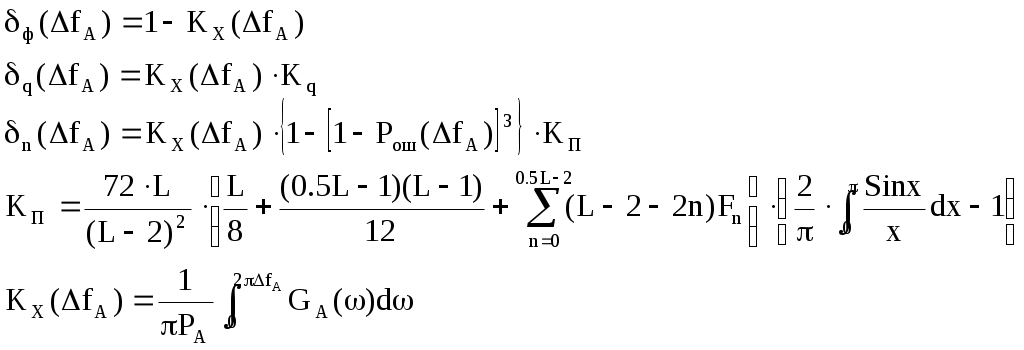 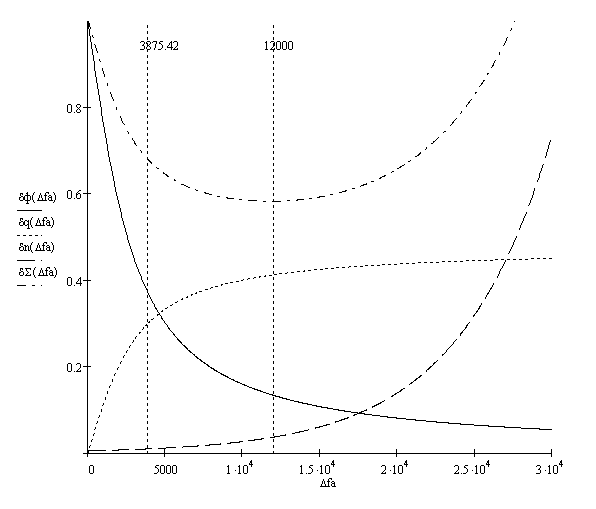 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
