Практическая. УСТс. Задания на контрольную работу по курсу устс
 Скачать 144 Kb.
|
|
| Варианты заданий | А | В | С | D | E | F |
| Вариант 5 | 5 | 5 | 5 | 5 | 5 | 5 |
А.5 Дать определение объекта управления (ОУ)
Объект управления (ОУ) - объект (или система объектов), для которого необходимо достичь желаемые цели управления через выдаваемые на него управляющие воздействия.
В.5 Линеаризуйте уравнение колебания физического маятника длинной L и массой m
Приведите линеаризованное уравнение.
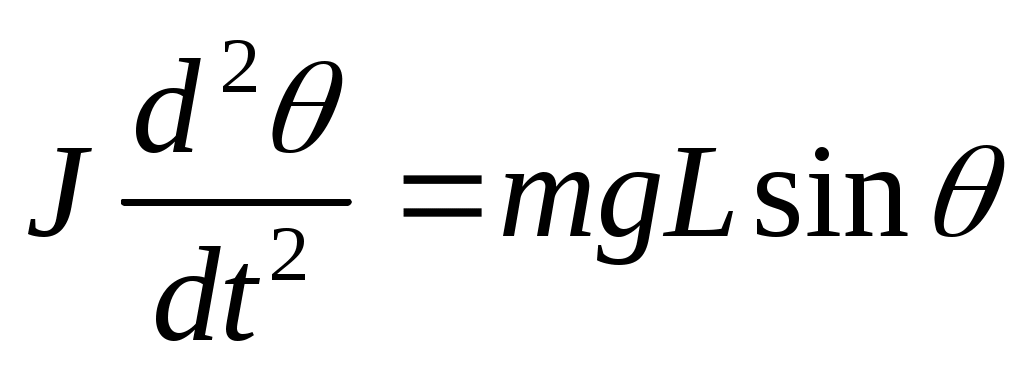
L
Из за относительной простоты получения решения всегда существовала и сейчас существует тенденция свести нелинейное уравнение к линейному операцией, так называемой, линеаризации. Это часто возможно сделать, если принять какое-то опорное состояние и записать уравнения системы в малых отклонениях – вариациях от этого опорного состояния. В предположении малости этих вариаций, поддерживаемых системой, можно получить линеаризованное уравнение системы. Рассмотрим колебания физического маятника.
L
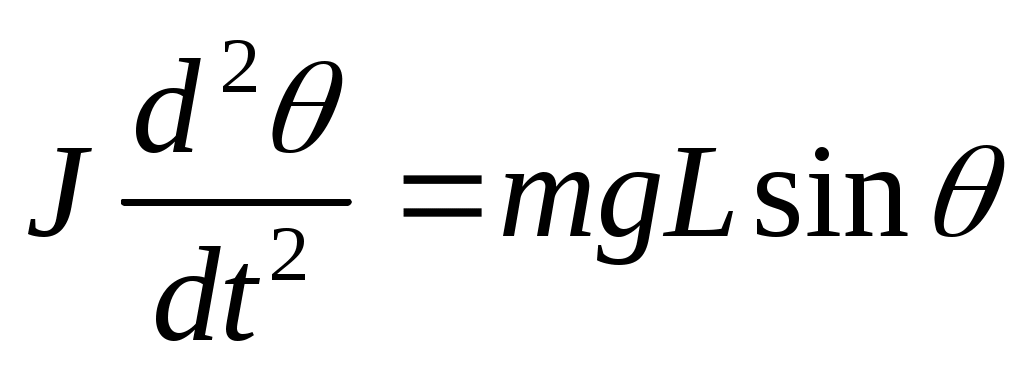
Это нелинейное уравнение относительно рассматриваемой координаты θ , которая является аргументом нелинейной функции sin. Однако, разложим функцию sin(θ) в степенной ряд.
+…..При малых θ – члены θ3 и θ5 гораздо меньше, чем θ и ими можно пренебречь. При
с ошибкой меньше чем 2% можно считать sin(θ)= θ.Итак уравнение колебаний маятника
- это линейное (линеаризованное) уравнение, справедливое для 
.С.5. Найти передаточную функцию замкнутой системы с обратной связью
Wзамк(s)=
= …..b(s)
. Передаточная функция объекта управления H(s)=
. Передаточная функция управляющего устройства в обратной связиH(s)=
G(s)= 
Передаточная функция замкнутой системы с отрицательной обратной связью.
b(s)
Y(s)=E(s)*G(s)
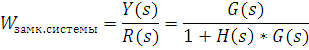
Передаточная функция замкнутой системы с отрицательной обратной связью равна передаточной функции объекта управления, поделенной на произведение передаточных функций объекта управления и управляющего устройства (передаточной функцией разомкнутой системы), сложенного с единицей.
Можно заметить, что система будет хорошо отслеживать входной сигнал R(s), когда
; это означает, что круговой коэффициент усиления системы 
и 
Тогда
Те же соображения позволяют определить как подавить возмущения, действующие на систему. Необходимо сделать передаточную функцию системы по возмущению
, при этом 
и 
.Д.5 Передаточная функция замкнутой системы управления имеет вид
W(s) =
= 
Здесь К1 > 0, К2 > 0, T1 > 0-Записать дифференциальное уравнение, связывающее выходную и входную координаты Z(t) и Y(t)
-Найти и записать характеристическое уравнение.
-Найти корни характеристического уравнения.
-Дать суждение об устойчивости системы
Передаточная функция системы управления имеет вид
W(s) =
= Тогда характеристическое уравнение:
Найдем корни характеристического уравнения:
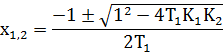
Необходимое, но недостаточное условие устойчивости – все коэффициенты характеристического уравнения должны иметь один знак.
Это условие совпадает.
Достаточное условие устойчивости для характеристического уравнения приводит к соотношению
≥ 0
≥ 0Это условие совпадает с предыдущим.
Дифференциальное уравнение, описывающее изменение по времени управляемой координаты t , полученное из передаточной функции
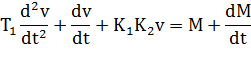
Е.5. В системе управления 2 исполнительных органа имеют встроенные ЦВМ и объединены с системной ЦВМ сетью по MILSTD 1553В. Системная ЦВМ является в данной сети контроллером, а ЦВМ исполнительных органов – оконечными устройствами. Определить через какое время выработанные в ЦВМ контроллера команды управления объемом по два слова данных на каждый исполнительный орган поступит на исполнение в исполнительные органы. При этом время передачи командного слова – 20мксек. Время передачи одного слова данных – 20мксек. Время передачи ответного слова(ОС) от оконечного устройства в контроллер – 20мксек.Пауза между окончанием передачи команды + данных и передачей ОС– 12мксек. Время в контроллере между окончанием приема ОС от первого сообщения и началом передачи командного слова на следующее ОУ – 50мксек.
Все сообщения, передаваемые в сети, имеют длину 20 бит и разделяются на три типа: командное слово, данные, ответное слово. В каждом двадцатибитном слове сообщений первые три бита – синхросигнал для вхождения в связь, а последний двадцатый бит – бит четности, для контроля целостности информации. Оставшиеся 16 бит слова данных это - данные. В ответном слове содержится информация об ОУ – его адресе, состоянии, наличии запроса на обслуживание.
В командном слове закодирован адрес ОУ, к которому обращается контроллер и команда, с которой контроллер обращается к ОУ. Команды могут быть нескольких типов:
-передача информации ОУ,
-получение (запрос)информации с ОУ,
-команда для ОУ без информации(например, дай ответное слово)и т.п.
Длительность передачи любого слова на частоте 1 МГГЦ составляет 20 мксек.
Кратко рассмотрим формат трех типов сообщений. Всего в стандарте их шесть.
Кроме этих форматов существует формат группового сообщения, формат передачи данных от ОУ к ОУ, но только по команде котроллера и т.п.
Пауза t2 формируется ОУ после полученного сообщения и должна быть 4-12 мсек. Отсутствие ответного слова через t2>12 мсек воспринимается контроллером как неполучение ОУ направленного ему сообщения.
Пауза t1 формируется контроллером и определяется временем работы его ПО, но она не может быть менее 4мксек.
Максимально число слов данных в сообщении равно 32.
Максимальное число ОУ на линии – 31 + с учетом адреса контроллера, так как общее число адресов устройств интерфейса в сети = 32. Среди команд управления, число которых в стандарте задано 15 (остальные - резервные), имеется команда к ОУ «дай ответное слово».
Если ОУ хочет по собственной инициативе начать передачу, то он этого сделать не может, но у него есть единственная возможность обратить на себя внимание контроллера и в конце концов передать имеющееся у него сообщение. Для этого ОУ в своем ответном слове на команду «дай ответное слово» или любую другую команду в 11 позиции ответного слова должен установить в 1 – бит флага «запрос на обслуживание».
Получив в ответном слове эту информацию, контроллер по собственной логике, заложенной в его ПО может запросить информацию с ОУ командой запроса данных (формат 2). Только после этого ОУ сможет передать свою информацию. Таким образом, ОУ могут проявлять контролируемую инициативу по передаче данных в линию. Забота о периодическом опросе флагов ОУ «запрос на обслуживание» лежит на контроллере, точнее на его ПО прикладного уровня, реализующем логику управления сетью.
Таким образом, передача из контроллера сообщения на 2 различных ОУ из двух слов данных на каждый займёт время
2(КС+12 мксек.+2СД+ ОС+ t1 )= 192 мксек.
Здесь КС, СД, ОС – времена передачи соответственно командного слова, слова данных, ответного слова, равные по 20 мксек.
Данные времена передачи данных применительно к мехатронной СТС являются достаточно малыми ( период повторения решения задачО,1 сек), т.е. сеть не вносит принципиального запаздывания в систему управления СТС.
F5. Поведение системы описывается дифференциальным уравнением
Необходимо получить решение данного уравнения методом Эйлера. Число шагов интегрирования n = 200 , шаг интегрирования
t= 0,05 сек., значение квадрата собственной частоты колебаний 
= 9[1/сек2] , значение относительного коэффициента демпфирования 
=0,2, значение постоянно действующего внешнего возмущения М=1[1/сек2]. Соотношения метода Эйлера необходимо реализовать либо в Mathcad, либо на любом другом языке программирования.
1.Привести представление данного уравнения в необходимой для решения методом Эйлера форме.
2.Привести график изменения
по времени для полученного решения3.Привести график изменения
по времени для решения с значением =0,7 при тех же остальных исходных данных1)
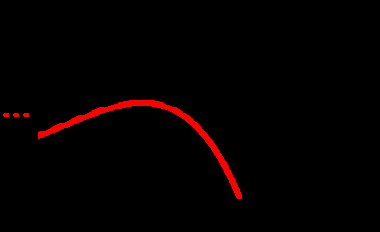2) график 
3) =0,7 Поволжский государственный университет телекоммуникаций и
Информатики
Заочный факультет
РЕГИСТРАЦИОННЫЙ № ______
Контрольная работа № _______ Вариант _______
по _____________________________________________________
Студент _________________________________________________
________________________________________________________
Факультет _________ курс ________ шифр __________ гр.______
Работа выслана «_____»_________________ 201__г.
Оценка _______________ Дата _______________201___г.
Подпись преподавателя ___________________