Курсовая ОЗЗ. Федеральное государственное автономное образовательное учреждение высшего образования Первый Московский государственный медицинский университет имени И.
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
Задание: проанализируйте структуру инвалидности населения города О., укажите на диаграмме приоритетные ранговые места (с 1 по 4), представьте информацию графически, сделайте вывод. Для анализа и построения диаграммы необходимо провести расчет удельного веса каждой причины в совокупности: (Количество инвалидов по данной причине∗100% )/Общее число инвалидов 1) Злокачественные новообразования: (350x100%)/1060=33,1% 2)Болезни системы кровообращения: (320x100%)/1060=30,2% 3)Последствия травм,отравлений и других внешних воздействий: (97x100%)/1060=9,2% 4) Болезни костно-мышечной системы и соединительной ткани: (85x100%)/1060=8,0% 5) Психические расстройства и расстройства поведения: (56x100%)/1060=5,3% 6) Эндокринные заболевания и болезни обмена: (38x100%)/1060=3,6% 7) Прочие: (114x100%)/1060=10,8%. Вывод: в структуре причин, приводящих к инвалидности, первое место занимают злокачественные новообразования (33,1%); второе место – болезни системы кровообращения (30,2%). А меньше всего эндокринные заболевания и болезни обмена (3,6%) приводят к инвалидности в городе О. Рисунок 13 «Основные заболевания, приводящие к первичной инвалидности населения города О. (абс. и в % к итогу)» 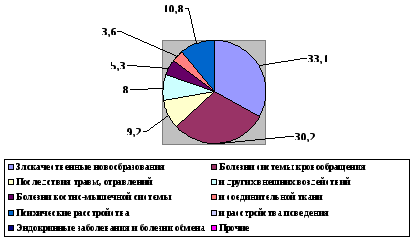 В изучаемом году врачами-стоматологами города О. и города М. соседней области под методическим руководством и при участии Московского ЦНИИ стоматологии было проведено сплошное эпидемиологическое исследование распространённости пародонтоза у жителей этих городов. Частота пародонтоза (на 1 000 жителей) в городе О. оказалась заметно выше. В тоже время было обращено внимание на различия в возрастной структуре населения городов О. и М. (таблица 9). Таблица 9 Распределение жителей городов О. и М. и больных пародонтозом по возрастным группам
Задание: с помощью соответствующего статистического метода оцените влияние возрастной структуры населения на частоту пародонтоза, сделайте вывод. Этапы расчета стандартизированных показателей: I этап Расчет общих и частных интенсивных показателей: (Число больных пародонтозом/Число жителей)х1000 Общие показатели заболеваемости для города О. и М. на 1000 населения: город О.: 10860х1000/100000 = 108,6 на 1000 жителей город М.: 12000х1000/100000 = 120 на 1000 жителей. Показатель заболеваемости пародонтозом для города О. на 1000 населения в зависимости от возраста больных (частные показатели): До 15 лет: 660 * 1000/23000 = 28,7‰ 15-49 лет: 3000 * 1000/50000 = 60,0‰ 50 и старше: 7200 * 1000/27000 = 266,7‰ Показатель заболеваемости пародонтозом для города М. на 1000 населения в зависимости от возраста больных (частные показатели): До 15 лет: 600 * 1000/26000 = 23,1‰ 15-49 лет: 3200 * 1000/50000 = 64‰ 50 и старше: 8200 * 1000/24000 = 341,7‰ II этап Определение стандарта: сумма числа жителей по каждой возрастной группе в обоих городах Стандарт для двух городов Возраст Стандарт до 15 лет 23000 + 26000 = 49000 15-49 50000 + 50000 = 100000 50 и старше 27000 + 24000 = 51000 Всего 100000 + 100000 = 200000 III этап Определение ожидаемого количества больных пародонтозом в стандарте по каждой возрастной группе в городах О. и М. с учетом соответствующих показателей заболеваемости : город О : До 15 лет: 1000 – 28,7 49000 – Х; Х = 28,7х49000/1000 = 1406,3 15-49 лет: 1000 – 60 100000 – Х; Х = 60х100000/1000 = 6000 50 и старше: 1000 –266,7 51000 – Х; Х = 266,7х51000/1000 = 13601,7. город М: До 15 лет: 1000 – 23,1 49000 – Х; Х = 23,1х49000/1000 = 1131,9 15-49 лет: 1000 – 64 100000 – Х; Х = 64х100000/1000 = 6400 50 и старше: 1000 –341,7 51000 – Х; Х = 341,7х51000/1000 = 17426,7. Сумма ожидаемых чисел больных пародонтозом в стандарте: город О.: 1406,3 + 6000 + 13601,7 = 21008,0 город М.: 1131,9 + 6400 + 17426,7 = 24958,6 IV этап Определение общих стандартизированных показателей заболеваемости пародонтозом в городах О. и М. город О.: 21008,0х1000/200000 = 105,4 на 1000 жителей город М.: 24958,6х1000/200000 = 124,8 на 1000 жителей
V этап Сопоставление соотношения интенсивных и стандартных показателей заболеваемости пародонтоза в городах О. и М.
Вывод:1. Уровень заболеваемости пародонтозом в городе М. выше, чем в городе О.; 2. Если бы возрастной состав жителей в этих городах был бы одинаков, то заболеваемость пародонтозом была бы также выше в городе М; 3. Следовательно, на различия в уровнях заболеваемости пародонтозом (в частности, на «завышение» ее в городе М. и «занижение» в городе О.) не оказывает влияние неоднородность возрастного состава жителей. В этом случае можно предположить, что на такую высокую заболеваемость пародонтозом в городе М. влияет такой фактор, как менее развитый город, поэтому происходят нарушения правил гигиены полости рта или эпидемиологические вспышки инфекции, которые влекут за собой снижение иммунитета. В изучаемом году сотрудниками районного родильного дома города О. проведён сравнительный анализ физического развития детей, рождённых женщинами различных возрастных групп (таблица 10). Таблица 10 Результаты измерения массы тела детей, рождённых женщинами в возрасте старше 35 лет
Задание: рассчитайте средний вес детей, рождённых женщинами в возрасте старше 35 лет, оцените разнообразие показателя, сделайте вывод. Мода = 3,5 кг; Медиана = 3,5 кг (26 место); Лимиты: минимум (V min) = 2,3 кг и максимум (V max) = 4,3 кг; Амплитуда(А) = V max - V min = 2 кг; Число наблюдений (n) = Σp= 51; Вариационный ряд: взвешенный; Расчет среднего веса и оценка разнообразия: М = ΣVp/n = (1 * 2,3 + 1 * 2,5 + 2,7 * 2 + 2,9 * 3 + 3,1 * 3 + 3,3 * 9 + 3,5 * 12 + 3,7 * 7 + 3,9 * 6 + 4,1 * 4 + 4,3 * 3)/51 = 3,5 кг. Для оценки разнообразия необходимо посчитать коэффициент вариации: d- разность каждой варианты от среднеарифметической (d = V – M) V- варианта M –средняя величина р – частота ∑d2р – сумма отклонений σ = √(∑ d2р)/n – среднеквадратическое отклонение CV = σ/M × 100% - коэффициент вариации ∑d2р = d12р1 + d22 р2 + d32 р3 + d42 р4 + d52 р5 + d62 р6 + d72 р7 + d82 р8 + d92 р9 + d102 р10 + d112 р11 = 1,44 + 1 + 1,28 + 1,08 + 0,48 + 0,36 + 0,28 + 0,96 + 1,44 + 1,92 = 10,24 σ = √(∑ d2р) / n = √10,24 / 51 = ± 0,45 СV = σ / M * 100% = 0,45 / 3,5 * 100% = 12,86%. Вывод: 1. Среднеарифметическая масса тела детей, рожденных женщинами старше 35 лет, равна 3,5 кг; 2. σ = ± 0,45 кг; 3. Величина коэффициента вариации, равная 12,9% свидетельствует о среднем разнообразии признака (приближающемся к слабому). Таким образом, можно считать, что полученная средняя величина массы тела является достаточно представительной (типичной). Дети, рождённые женщинами в возрасте 20-29 лет, имели среднюю массу тела 3,2 кг ( = 0,3 кг, Сv = 9,1 %, m = 0,03 кг). Задание: сравните разнообразие показателя массы тела детей, рождённых женщинами различных возрастных групп, сделайте вывод. Оцените влияние возраста женщин на массу тела детей при рождении, сделайте вывод. 1. Средняя масса тела детей, рожденных женщинами в возрасте 20-29 лет в городе О. составляет 3,2 кг; 2. s = ±0,3 кг; 3. Величина коэффициента вариации, равная 9,1% свидетельствует о слабом разнообразии признака, приближающегося к среднему. 4. Коэффициент Стьюдента (критерий достоверности) t=,где t=критерий достоверности; m1 и m2 - ошибки репрезентативности; M1 и М2 - средние величины; M1 (для женщин старше 35 лет) = 3,5кг; M2 (для женщин 20-29 лет) = 3,2кг; m1 (для женщин старше 35 лет) = ±0,45/√51= ±0,06 кг; m2 (для женщин 20-29 лет) = ±0,03 кг; t = (3,5-3,2)/ √(0,06^2+ 0,03^2)=4,5 > 2 Если t ≥ 2, что соответствует вероятности безошибочного прогноза Р ≥ 95,5%, то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что будет иметь место и в генеральной совокупности. Вывод: значение критерия t = 4,5 соответствует вероятности безошибочного прогноза Р>99,7%, следовательно, можно утверждать, что различие в средних значениях средней массы новорожденных у женщин старше 35 лет и 20-29 лет не случайно, а достоверно, существенно. Очевидно, что с увеличением возраста роженицы, также увеличивается и масса тела новорожденного. Разнообразие массы тела детей, рожденных женщинами старше 35 лет среднее (величина коэффициента вариации, равная 12,9% свидетельствует о среднем разнообразии признака (приближающемся к слабому)), а разнообразие массы тела детей, рожденных женщинами в возрасте 20-29 лет, является слабым (величина коэффициента вариации, равная 9,1% свидетельствует о слабом разнообразии признака, приближающегося к среднему). Следовательно, величина средней массы тела детей у женщин, родивших в 20-29 лет, является более представительной (типичной) для изучаемой совокупности. А для величины массы тела детей, рожденных женщинами старше 35 лет, отмечается более значительная вариабельность данного значения. Врачи детской поликлиники совместно с медицинскими работниками школ города О. провели выборочное обследование старшеклассников на предмет выявления заболеваний желудочно-кишечного тракта (ЖКТ). Осмотрено 540 учащихся 9, 10 и 11-х классов, заболевания ЖКТ обнаружены у 80. Задание: оцените частоту заболеваний ЖКТ у старшеклассников, с помощью соответствующего статистического метода сделайте прогноз о частоте ЖКТ для генеральной совокупности учащихся 9, 10 и 11-х классов. 1. Оценка частоты заболеваний ЖКТ рассчитывается по формуле: (число больных∗100%)/число осмотренных учащихся Вся совокупность – 540 человек принимается за 100%, составные части определяются как искомые. Частота заболеваний ЖКТ составляет: (80∗100%)/540 =14,8%. 2. Для прогноза о частоте заболеваний ЖКТ для генеральной совокупности учащихся 9, 10 и 11-х классов необходимо применить метод оценки доверительных границ для относительных показателей с предварительным расчетом ошибки репрезентативности относительного показателя. А) Вычисление ошибки репрезентативности относительного показателя: m=√(��∗��)/�� Так как показатель p выражен в %, q = (100 – p) m=√(14,8∗(100−14,8))/540= ±1,53% Б) Вычисление доверительных границ средней величины генеральной совокупности (Рген): Расчет по формуле: Pген = Рвыб ± tm, где Pген – значение относительного показателя генеральной совокупности Рвыб – значение относительного показателя выборочной совокупности; t – критерий достоверности; m – ошибка репрезентативности. Для вычисления необходимо: а) задать степень вероятности безошибочного прогноза (Р = 95,5%); б) определить величину критерия t, при заданной степени вероятности и числе наблюдений больше 30 величина критерия t равна 2 (t = 2). Тогда Pген = Рвыб ± mt = 14,8% ± 1,53 * 2 = от 11,74% до 17,86% Вывод:Частота нарушения ЖКТ для выборочной совокупности учащихся 9, 10, 11 классов соответствует 14,8%. Установлено с вероятностью безошибочного прогноза Р = 95,5%, что частота нарушения ЖКТ для генеральной совокупности учащихся 9, 10, 11 классов будет находиться в пределах от 11,74% до 17,86% случаев, т.е. частота заболеваний ЖКТ ниже 11,74% и выше 17,86% возможна не более чем у 4,5% случаев генеральной совокупности. С целью разработки мероприятий по снижению профессиональной заболеваемости рабочих литейного завода врачами поликлиники было проведено изучение влияния стажа работы на уровень заболеваний органов дыхания у рабочих (таблица 11). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
