математические методы в психологии. мат.методы в психологии Ушакова А.И.. Федеральное государственное бюджетное образовательное учреждение высшего образования башкирский государственный педагогический университет им. М. Акмуллы
 Скачать 414.5 Kb. Скачать 414.5 Kb.
|
|
13.Критерии выявления различий в уровне исследуемого признака: критерии Розенбаума, Манна-Уитни. Ограничения в применении Q – критерий Розенбаума Критерий используется для оценки различий между о. В каждой из выборок должно быть не менее 11 испытуемых (значений) двумя выборками по уровню какого-либо признака, измеренного количественно. Непараметрический критерий, позволяющий оценить различие между двумя выборкам и по уровню какого-либо признака. (Невыявленность достоверных различий с помощью этого критерия, строго говоря, не означает их отсутствия, а указывает на необходимость применения более мощного критерия, например j* Фишера.) Если Q – критерий выявил достоверное различие с уровнем значимости p<= (меньше или равно) 0,01 – можно ограничиться только его применением. Критерий применим в тех случаях, когда данные представлены, по крайней мере, в порядковой шкале. Признак должен варьировать в некотором диапазоне значений – в противном случае применение критерия невозможно. Например, если имеется только 3 значения признака – Х1, Х2, Х3 – установить различия очень трудно. Метод Розенбаума требует, соответственно, достаточно тонко измеренных признаков. Применение критерия начинается с упорядочивания значений признака в обеих выборках по нарастанию (или убыванию). (Для удобства каждое значение можно представить на отдельной карточке с целью их последующей систематизации.) Гипотезы: Но: Уровень признака в выборке 1 не превышает уровня признака в выборке 2. Н1: Уровень признака в выборке 1 превышает уровень признака в выборке 2. Ограничения критерия Q В каждой из выборок должно быть не менее 11 наблюдений. Объемы выборок должны примерно совпадать: Меньше 50 наблюдений – разница не более 10; От 50 до 100 наблюдений – не больше 20; Больше ста наблюдений, то одна из выборок не должна быть больше другой более чем в 1,5 – 2 раза. Диапазоны разброса значений в двух выборках не должны совпадать между собой, иначе применение критерия бессмысленно. Алгоритм ранжирования. 1) Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. (Например, если n = 7, то наибольшее значение получит ранг 7.) 2) В случае если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны. Не следует путать понятие ранга и понятия порядкового номера! При ранжировании мы выбираем в качестве следующего значения не следующее «по списку», а следующее по величине.) 3) Общая сумма рангов должна совпадать с расчетной, которая вычисляется по формуле: S (Ri) = N(N+1) / 2 Где N – общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной суммы рангов свидетельствует о допущенной ошибке при начислении рангов или при их суммировании! U – критерий Манна-Уитни Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n1 и n2 больше или равны 3 (либо n1 = 2, а n2 тогда больше или равно 5.) Метод определяет, достаточно ли мала зона пересекающихся значений между двумя рядами. Чем меньше эта область, тем более вероятно, что различия достоверны. Эмпирическое (фактически полученное) значение критерия U отражает то, насколько велика зона совпадения между рядами. Чем меньше Uэмп., тем более вероятно, что различия достоверны. Гипотезы. Но: Уровень признака в группе 2 не ниже уровня признака в группе 1. Н1: Уровень признака в группе 2 ниже уровня признака в группе 1. Ограничения критерия U. 1. В каждой выборке должно быть не менее 3 наблюдений или, в крайнем случае, допускается соотношение 2 к 5 или более. 2. В каждой выборке должно быть не более 60 наблюдений. Алгоритм подсчета критерия U – Манна-Уитни. 1.Перенести все данные выборок на индивидуальные карточки (на которых цветом или как-то еще будет отражено, к какой из выборок принадлежит значение). 2. Разложить все карточки в общий ряд по мере нарастания признака, не считаясь с тем, к какой выборке они относятся. 3. Проранжировать (согласно алгоритму ранжирования) значения на карточках, приписывая меньшему значению меньший ранг. Всего рангов должно быть n1 + n2 (объем первой выборки + объем второй выборки). 4. Заново разложить карточки в два ряда, по признаку принадлежности к выборке 1 или выборке 2. 5. Подсчитать сумму рангов отдельно на карточках группы 1 и группы 2. Проверить совпадение общей суммы рангов с расчетной. 6. Определить большую из двух ранговых сумм. 7. Определить значение U по формуле: 8. Определить из таблиц критические значения U, в соответствии с этим, принять либо отклонить гипотезу Но. 14.Критерии выявления различий в уровне исследуемого признака: критерии Краскела-Уоллиса, Джонкира. Ограничения в применении. Н – критерий Крускала - Уоллиса Критерий Н применяется для оценки различий по степени выраженности анализируемого признака одновременно между тремя, четырьмя и более выборками. Он позволяет выявить степень изменения признака в выборках, не указывая, однако, на направление этих изменений. Критерий основан на том принципе, что чем меньше взаимопересечение выборок, тем выше уровень значимости Нэмп. Следует подчеркнуть, что в выборках может быть разное количество испытуемых, хотя в приведенных ниже задачах приводится равное число испытуемых в выборках. Работа с данными начинается с того, что все выборки условно объединяются по порядку встречающихся величин в одну выборку и значениям этой объединенной выборки проставляются ранги. Затем полученные ранги проставляются исходным выборочным данным и по каждой выборке отдельно подсчитывается сумма рангов. Критерий построен на следующей идее – если различия между выборками незначимы, то и суммы рангов не будут существенно отличаться одна от другой и наоборот. Величина Нэмп подсчитывается по формуле: Нэмп 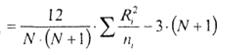 Где N – общее число членов в обобщенной выборке; ni – число членов в каждой отдельной выборке; При определении критических значений критерия применительно к четырем и более выборкам используют таблицу для критерия хи-квадрат, подсчитав предварительно число степеней свободы v для с = 4. Тогда v = с – 1 = 4 – 1=3.. Подчеркнем, что если использовать критерии, позволяющие сравнивать только два ряда значений, то полученный выше результат потребовал бы шести сравнений – первая выборка со второй, третьей и т.д. Для использование критерия Н необходимо соблюдать следующие условия: 1. Измерение должно быть проведено в шкале порядка, интервалов или отношений. 2. Выборки должны быть незагисимыми. 3. Допускается разное число испытуемых в сопоставляемых выборках. 4. При сопоставлении трех выборок допускается, чтобы в одной из них было n = 3, а в двух других n = 2. Однако в таком случае различия могут быть зафиксированы лишь на 5 % уровне значимости. 6. При большем числе выборок и разном количестве испытуемых в каждой выборке следует пользоваться таблицей для критерия хи-квадрат. В этом случае число степеней свободы при этом определяется по формуле: v = с – 1, где с – количество сопоставляемых выборок. S – критерий тенденций Джонкира Этот критерий ориентирован на выявление тенденций изменения измеряемого признака при сопоставлении от трех и до шести выборок. В отличие от предыдущего критерия Я, количество элементов в каждой выборке должно быть одинаковым. Если же число элементов в каждой выборке различно, то необходимо случайным образом уравнять выборки, при этом неизбежно утрачивается часть информации. Если же потеря информации покажется слишком расточительной, то следует воспользоваться вышеприведенным критерием Н – Крускала–Уоллиса, хотя в этом случае нельзя будет выдвигать гипотезу о наличии или отсутствии искомых тенденций. Критерий S основан на следующем принципе: все выборки располагаются слева направо в порядке возрастания значений исследуемого признака. При этом выборка, в которой среднее значение или сумма всех значений меньше, чем в остальных выборках, располагается слева, а выборка, в которой эти же значения выше, располагается правее и так далее. После такого упорядочивания для каждого отдельного элемента, стоящего слева в выборке, подсчитывается число инверсий по отношению ко всем элементам упорядоченных выборок, расположенных правее. Инверсией для данного элемента выборки считается число элементов, которые превышают данный элемент по величине по всем выборкам справа. Инверсии по отношению к собственной выборке, т.е. той, в которой находится данный элемент, не подсчитываются. В соответствии с этим правилом у последнего столбца выборки инверсии также не подсчитываются, т.к. справа больше нет данных. Правило подсчета инверсий позволяет утверждать, что чем выше величина инверсий у крайних правых столбцов, тем выше уровень значимости статистики S. Следующий этап – подсчет общей суммы получившихся инверсий. Это число обозначается как А. В нашем примере оно равно А = 30 + 18 + 10 = 58. Величина S критерия вычисляется по формуле: В формуле символ В также представляет собой выражение:  где n – количество элементов в столбце (группе) с – количество столбцов (групп). Для использования критерия S необходимо соблюдать следующие условия: 1. Измерение может быть проведено в шкале порядка, интервалов и отношений. 2. Выборки должны быть независимыми. 3. Количество элементов в каждой выборке должно быть одинаковым. Если это не так, то необходимо случайным образом уравнять выборки. 4. Нижняя граница применимости критерия: не менее трех выборок и не менее двух элементов в каждом наблюдении. Верхняя граница определяется таблицей 10 Приложения – не более 6 выборок и не более 10 элементов в каждой выборке. Во всех других случаях следует пользоваться критерием Н. 15.Оценка достоверности сдвига в значениях исследуемого признака: критерии знаков, Вилкоксона, Фридмана, Пейджа. Ограничения в применении. В психологических исследованиях часто бывает важно доказать, что в результате действия каких-либо факторов произошли достоверные изменения («сдвиги») в измеряемых показателях. Сдвиг – это разность между вторым и первым замерами показателей измеряемого признака у одного испытуемого. Сдвиги могут быть как отрицательными, так и положительными. Сдвиги, которые кажутся преобладающими, называют типичными, а сдвиги более редкого, противоположного направления – нетипичными. В зависимости от условий измерения различают сдвиги временные, ситуационные, умозрительные, структурные и сдвиги под влиянием экспериментального воздействия. Временной сдвиг – сопоставление показателей, полученных у одних и тех же испытуемых по одним и тем же методикам, но в разное время. Многократные обследования одних и тех же лиц на протяжении достаточно длительного отрезка их жизненного пути называются лонгитюдинальным исследованием. Ситуационный сдвиг – сопоставление показателей, полученных по одним и тем же методикам, но в разных условиях измерения (например, «покоя» и «стресса»). Умозрительный сдвиг – сопоставление показателей, измеренных в обычных и воображаемых условиях. Например, можно попросить испытуемого «представить себе», что он оказался в других условиях измерения: в будущем, в позиции других людей, которые оценивают его как бы со стороны, в состоянии разгневанного отца и т. п. Структурные сдвиги– сопоставление между собой разных показателей одних и тех же испытуемых, если они измерены в одних и тех же единицах, по одной и той же шкале. Назначение Т– критерия Вилкоксона Критерий применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность. С его помощью мы определяем, является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом. Условия применения Т– критерия Вилкоксона 1) Измерение может быть проведено во всех шкалах, кроме шкалы номинальной. 2) Выборка должна быть связной. 3) Число элементов в сравниваемых выборках должно быть равным. 4) Минимальное количество испытуемых, прошедших измерения в двух условиях, – 5 человек. Максимальное количество испытуемых – 50 человек. 5) Нулевые сдвиги из рассмотрения исключаются, и количество наблюдений n уменьшается на количество этих нулевых сдвигов. Критерий Фридмана применяется для сопоставления показателей, измеренных в c условиях (c≥3) на одной и той же выборке из n испытуемых. Критерий Фридмана позволяет установить, что величины показателей от условия к условию изменяются, но при этом не указывает на направление изменений и в этом смысле похож на критерий знаков. Критерий Фридмана является обобщением критерия Вилкоксона на большее, чем два, количество условий измерения, в котором мы ранжируем не абсолютные величины сдвигов, а сами индивидуальные значения измерений. Ограничения критерия: минимальное количество испытуемых лиц п> 2, каждое лицо должно пройти более трех испытаний с> 3. Критерий L Пейджа применяется для сопоставления показателей, измеренных в трех и более условиях на одной и той же выборке испытуемых. Критерий позволяет выявить тенденции в изменении величин признака при переходе от условия к условию. Его можно рассматривать как продолжение теста Фридмана, поскольку он не только констатирует различия, но и указывает на направление изменений. Ограничения критерия Пейджа. 1. Нижний порог - 2 испытуемых, каждый из которых прошел не менее 3-х замеров в разных условиях. Верхний порог - 12 испытуемых и 6 условий (n<12, с<6). 16.t-критерий Стьюдента, использование для оценки различий выборочных средних. Ограничения в применении. Наиболее часто в психологическом исследовании встречается задача выявления различий между двумя или более группами признаков. Выявление таких различий на уровне средних арифметических мы уже рассмотрели выше в процедуре анализа первичных статистик. Однако, возникает вопрос насколько эти различия достоверны и можно ли их распространить (экстраполировать) на всю популяцию. Для решения этой задачи чаще всего используется (при условии нормального или близкого к нормальному распределения) t-критерий (или критерий Стьюдента). Этот критерий предназначен для того, чтобы выяснить, на сколько достоверно различаются показатели одной выборки испытуемых от другой (например, когда испытуемые получают в результате тестирования одной группы более высокие баллы, чем представители другой). Это параметрический критерий, имеющий две основные формы. Первая из них - несвязанный t-критерий (который также называют непарным t-критерием) - предназначен для того, чтобы выяснить, имеются ли различия между оценками, полученными при использовании одного и того же теста для тестирования двух групп, составленных из разных людей. Критерий называется «несвязанным», потому что сравниваемые группы составлены из разных людей. Связанный t-критерий (который иногда называют парным t-критерием) предназначен для сравнения показателей двух групп, между членами которых существует специфическая связь. Это означает, что каждому члену первой группы соответствует какой-либо член второй группы, который похож на него по какому-то параметру, интересующему исследователя. Чаще всего сравниваются параметры одних и тех же людей до и после определенного события или воздействия (например, в процессе проведения лонгитюдного исследования или формирующего эксперимента). Поэтому данный критерий используется для сравнения показателей одних и тех же людей до и после обследования, эксперимента или прошествии некоторого времени. Критерий позволяет найти вероятность того, что оба средних значения в выборке относятся к одной и той же совокупности. Данный критерий наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности». 17.F- критерий Фишера при оценке различий выборочных дисперсий. Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова: 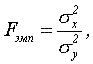 где - дисперсии первой и второй выборки соответственно. Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение Fэмп всегда будет больше или равно единице. Число степеней свободы определяется также просто: k1=nl - 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k2=n2 - 1 для второй выборки. 18.Выявление различий в распределении признака - критерий 2 – Пирсона. Ограничения в применении. Распределения могут различаться по средним, дисперсиям, асимметрии, эксцессу и по сочетаниям этих параметровТрадиционные для отечественной математической статистики критерии определения расхождения или согласия распределений – это метод χ2 – К. Пирсона и λ-критерий Колмогорова- Смирнова. Оба эти метода требуют тщательной группировки данных и довольно сложных вычислений. Кроме того, возможности этих критериев в полной мере проявляются на больших выборках (n>30). Тем не менее, они могут оказаться столь незаменимыми, что исследователю придется пренебречь экономией времени и усилий. Например, они незаменимы в следующих двух случаях: 1) в задачах, требующих доказательства неслучайности предпочтений в выборе из нескольких альтернатив; 2) в задачах, требующих обнаружения точки максимального расхождения между двумя распределениями, которая затем используется для перегруппировки данных с целью применения критерия ϕ* (углового преобразования Фишера). Назначения критерия. Критерий χ2 применяется в двух целях: 1) для сопоставления эмпирического распределения признака с теоретическим – равномерным, нормальным или каким-то иным; 2) для сопоставления двух трех или более эмпирических распределений одного и того же признака На самом деле области применения критерия χ2 многообразны, но мы ограничиваемся только этими двумя, наиболее часто встречающимися на практике, целями). Описание критерия. Критерий χ2 отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях. Преимущество метода состоит в том, что он позволяет сопоставлять распределения признаков, представленных в любой шкале, начиная от шкалы наименований. В самом простом случае альтернативного распределения "да – нет", "допустил брак – не допустил брака", "решил задачу – не решил задачу". При сопоставлении эмпирического распределения с теоретическим мы определяем степень расхождения между эмпирическими и теоретическими частотами. При сопоставлении двух эмпирических распределений мы определяем степень расхождения между эмпирическими частотами и теоретическими частотами, которые наблюдались бы в случае совпадения двух этих эмпирических распределений. Формулы расчета теоретических частот будут специально даны для каждого варианта сопоставлений. Чем больше расхождение между двумя сопоставляемыми распределениями, тем больше эмпирическое значение χ2 . Гипотезы. Возможны несколько вариантов гипотез, в зависимости от задач, которые мы перед собой ставим. Первый вариант: H0: Полученное эмпирическое распределение признака не отличается от теоретического (например, равномерного) распределения. H1: Полученное эмпирическое распределение признака отличается от теоретического распределения. Второй вариант: H0: Эмпирическое распределение 1 не отличается от эмпирического распределения 2. H1: Эмпирическое распределение 1 отличается от эмпирического распределения 2. Третий вариант: H0: Эмпирические распределения 1, 2, 3,... не различаются между собой. Н1: Эмпирические распределения 1, 2, 3, ... различаются между собой. Критерий χ2 позволяет проверить все три варианта гипотез. Ограничения критерия. 1) Объем выборки должен быть достаточно большим: n>.30. 2) Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5: ƒ≥5. Это означает, что если число разрядов задано заранее и не может быть изменено, то мы не можем применять метод, χ2 не накопив определенного минимального числа наблюдений. 3) Выбранные разряды должны "вычерпывать" все распределение, то есть охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопоставляемых распределениях. 4) Необходимо вносить "поправку на непрерывность" при сопоставлении распределений признаков, которые принимают всего 2 значения. При внесении поправки значение χ2 уменьшается 5) Разряды должны быть неперекрещивающимися: если наблюдение отнесено к одному разряду, то оно уже не может быть отнесено ни к какому другому разряду. Сумма наблюдений по разрядам всегда должна быть равна общему количеству наблюдений. |
