математические методы в психологии. мат.методы в психологии Ушакова А.И.. Федеральное государственное бюджетное образовательное учреждение высшего образования башкирский государственный педагогический университет им. М. Акмуллы
 Скачать 414.5 Kb. Скачать 414.5 Kb.
|
|
19.Многофункциональный статистический критерий φ*-угловое преобразование Фишера. Ограничения в применении Многофункциональные критерии позволяют решать задачи сопоставления уровней исследуемого признака, сдвигов в значениях исследуемого признака и сравнения распределений. К числу многофункциональных критериев в полной мере относится критерий φ* Фишера (угловое преобразование Фишера) и, с некоторыми оговорками - биномиальный критерий m. Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта (показателя). Чем он больше, тем достовернее различия. Критерий оценивает достоверность различий между теми процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект (показатель). Образно говоря, мы сравниваем между собой 2 лучших куска, вырезанные из 2-х пирогов, и решаем, какой из них действительно больше. Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла , который измеряется в радианах . Большей процентной доле будет соответствовать больший угол ф, а меньшей доле - меньший угол, но соотношения здесь не линейные: где Р - процентная доля, выраженная в долях единицы (см. Рис. 5.1). 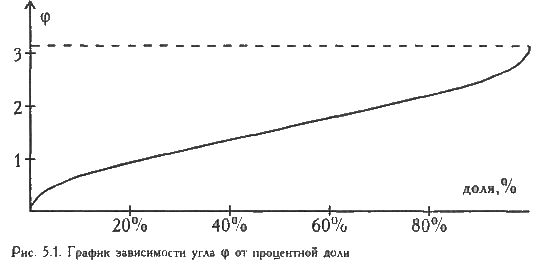 При увеличении расхождения между углами φ1 и φ2 и увеличения численности выборок значение критерия возрастает. Чем больше величина φ* , тем более вероятно, что различия достоверны. Гипотезы H0: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2. H1: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2. Графическое представление критерия φ* Метод углового преобразования несколько более абстрактен, чем остальные критерии. Формула, которой придерживается Е. В. Гублер при подсчете значений φ, предполагает, что 100% составляют угол φ=3,142, то есть округленную величину π=3,14159... Это позволяет нам представить сопоставляемые выборки в виде двух полукругов, каждый из которых символизирует 100% численности своей выборки. Процентные доли испытуемых с "эффектом" будут представлены как секторы, образованные центральными углами φ. Критерий φ* позволяет определить, действительно ли один из углов статистически достоверно превосходит другой при данных объемах выборок. Ограничения критерия φ* 1. Ни одна из сопоставляемых долей не должна быть равной нулю. Формально нет препятствий для применения метода φ в случаях, когда доля наблюдений в одной из выборок равна 0. Однако в этих случаях результат может оказаться неоправданно завышенным (Гублер Е.В., 1978, с. 86). 2. Верхний предел в критерии φ отсутствует - выборки могут быть сколь угодно большими. Нижний предел - 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок: а) если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30: б) если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7: в) если в одной из выборок всего 4 наблюдения, то во второй должно быть не менее 5: г) при n1,n2 ≥ 5 возможны любые сопоставления. В принципе возможно и сопоставление выборок, не отвечающих этому условию, например, с соотношением n1=2, n2=15, но в этих случаях не удастся выявить достоверных различий. Других ограничений у критерия φ* нет. 20.Корреляционный анализ: сущность корреляционного анализа, задачи решаемые в психологии методами корреляционного анализа, диаграмма рассеивания Корреляционный анализ – это проверка гипотез о связях между переменными с использованием коэффициентов корреляции, двумерной описательной статистики, количественной меры взаимосвязи (совместной изменчивости) двух переменных. Таким образом, это совокупность методов обнаружения корреляционной зависимости между случайными величинами или признаками. Корреляционный анализ для двух случайных величин заключает в себе: построение корреляционного поля и составление корреляционной таблицы; вычисление выборочных коэффициентов корреляции и корреляционных отношений; проверку статистической гипотезы значимости связи. Основное назначение корреляционного анализа – выявление связи между двумя или более изучаемыми переменными, которая рассматривается как совместное согласованное изменение двух исследуемых характеристик. Данная изменчивость обладает тремя основными характериcтиками: формой, направлением и силой. задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции. В настоящее время разработано множество различных коэффициентов корреляции. Наиболее применяемыми являются r-Пирсона, r-Спирмена и τ-Кендалла. Современные компьютерные статистические программы в меню «Корреляции» предлагают именно эти три коэффициента, а для решения других исследовательских задач предлагаются методы сравнения групп. Таким образом, условия применения коэффициентов корреляции будут следующими: переменные, измеренные в количественной (ранговой, метрической) шкале на одной и той же выборке объектов; связь между переменными является монотонной. Диаграмма рассеяния – один из инструментов статистического контроля, анализа. С ее помощью выявляется зависимость и характер связи между двумя разными параметрами экономического явления, производственного процесса. Диаграмма разброса показывает вид и тесноту взаимосвязи между парами данных. 21.Коэффициент линейной корреляции rx,y – Пирсона. Ограничения в применении. Примеры использования. Коэффициент корреляции Пирсона (r-Пирсона) применяется для исследования взаимосвязи двух переменных, измеренных в метрических шкалах на одной и той же выборке. Он позволяет определить, насколько пропорциональная изменчивость двух переменных. Данный коэффициент разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х годах XIX века. Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы. Коэффициент корреляции r-Пирсона характеризует существование линейной связи между двумя величинами. Если связь криволинейная то он не будет работать. Чтобы приступать к расчетам коэффициента корреляции r-Пирсона необходимо выполнение следующих условий: Исследуемые переменные X и Y должны быть распределены нормально. Исследуемые переменные X и Y должны быть измерены в интервальной шкале или шкале отношений. Количество значений в исследуемых переменных X и Y должно быть одинаковым. При расчете коэффициент линейной корреляции Пирсона используется специальная формула. Величина коэффициента корреляции варьируется от 0 до 1. Слабыми сторонами линейного коэффициента корреляции Пирсона являются: Неустойчивость к выбросам. С помощью коэффициента корреляции Пирсона можно определить только силу линейной взаимосвязи между переменными, другие виды взаимосвязей выявляются методами регрессионного анализа. 22.Коэффициенты связи для порядковых данных. Ранговый коэффициент корреляции Спирмена. Ограничения в применении. Коэффициент ранговой корреляции Спирмена является непараметрическим аналогом классического коэффициента корреляции Пирсона, но при его расчете учитываются не связанные с распределением показатели сравниваемых переменных (среднее арифметическое и дисперсия), а ранги. Например, необходимо определить связь между ранговыми оценками качеств личности, входящими в представление человека о своем «Я реальном» и «Я идеальном». Коэффициент Спирмена широко используется в психологических исследованиях. Например, в работе Ю. В. Бушова и Н. Н. Несмеловой [1]: для изучения зависимости точности оценки и воспроизведения длительности звуковых сигналов от индивидуальных особенностей человека был использован именно он. Так как этот коэффициент – аналог r-Пирсона, то и применение его для проверки гипотез аналогично применению коэффициента r-Пирсона. То есть проверяемая статистическая гипотеза, порядок принятия статистического решения и формулировка содержательного вывода – те же. В компьютерных программах (SPSS, Statistica) уровни значимости для одинаковых коэффициентов r-Пирсона и r-Спирмена всегда совпадают. Преимущество коэффициента r-Спирмена по сравнению с коэффициентом r-Пирсона – в большей чувствительности к связи. Мы используем его в следующих случаях: наличие существенного отклонения распределения хотя бы одной переменной от нормального вида (асимметрия, выбросы); появление криволинейной (монотонной) связи. Ограничением для применения коэффициента r-Спирмена являются: по каждой переменной не менее 5 наблюдений; коэффициент при большом количестве одинаковых рангов по одной или обеим переменным дает огрубленное значение. 23.Вычисление коэффициентов корреляции: коэффициент ассоциации Пирсона (фи – критерий), бисериальный критерий. Условия применения. Для изучения взаимосвязи двух метрических переменных, измеренных на одной и той же выборке, применяется коэффициент корреляции r-Пирсона. Сам коэффициент характеризует наличие только линейной связи между признаками, обозначаемыми, как правило, символами X и Y. Коэффициент линейной корреляции является параметрическим методом и его корректное применение возможно только в том случае, если результаты измерений представлены в шкале интервалов, а само распределение значений в анализируемых переменных отличается от нормального в незначительной степени. Существует множество ситуаций, в которых его применение целесообразно. Например: установление связи между интеллектом школьника и его успеваемостью; между настроением и успешностью выхода из проблемной ситуации; между уровнем дохода и темпераментом и т. п. Коэффициент Пирсона находит широкое применение в психологии и педагогике. Например, в работах И. Я. Каплуновича [6, с. 115] и П. Д. Рабиновича, М. П. Нуждиной [9, с. 112] для подтверждения выдвинутых гипотез был использован расчет коэффициента линейной корреляции Пирсона. При обработке данных «вручную» необходимо вычислить коэффициент корреляции, а затем определить p-уровень значимости (в целях упрощения проверки данных пользуются таблицами критических значений rxy, которые составлены с помощью этого критерия). Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем –1. Эти два числа +1 и –1 являются границами для коэффициента корреляции. Когда при расчете получается величина, большая +1 или меньшая –1, это свидетельствует, что произошла ошибка в вычислениях. При вычислениях на компьютере статистическая программа (SPSS, Statistica) сопровождает вычисленный коэффициент корреляции более точным значением p-уровня. Для статистического решения о принятии или отклонении H0 обычно устанавливают α = 0,05, а для большого объема наблюдений (100 и более) α = 0,01. Если p ≤ α, H0 отклоняется и делается содержательный вывод, что обнаружена статистически достоверная (значимая) связь между изучаемыми переменными (положительная или отрицательная – в зависимости от знака корреляции). Когда p > α, H0 не отклоняется, содержательный вывод ограничен констатацией, что связь (статистически достоверная) не обнаружена. Если связь не обнаружена, но есть основания полагать, что связь на самом деле есть, следует проверить возможные причины недостоверности связи. 24.Выбор коэффициента корреляции в соответствии с типом измерительных шкал (качественные, порядковые, количественные). Следует обязательно учитывать тип шкалы, с помощью которой измерены включенные в анализ переменные. Если нам необходимо оценить интенсивность связи между двумя признаками, один из которых измерен с помощью интервальной шкалы, а второй — с помощью номинальной шкалы (например, отношение к ценности «реформа» жителей Санкт-Петербурга разного возраста), то оптимальным является использование коэффициента корреляции Пирсона. Традиционным для выполнения корреляционного анализа является обращение к коэффициенту корреляции Пирсона (Pearson) Р (в литературе он обозначается и через гх). Формально для использования этого коэффициента должны выполняться следующие требования: переменные должны быть измерены с помощью, как минимум, интервальной шкалы (очевидно, что в области политологии не так много переменных могут быть измерены с помощью интервальных шкал или абсолютных метрических шкал, среди них возраст, партийный стаж, стаж работы в органах власти); связь между переменными должна быть линейной (если связь является монотонной, но не линейной, используют коэффициенты корреляции Спирмена или Кендалла); включенные в анализ переменные должны иметь нормальное (или хотя бы приближенное к нормальному) распределение. 25.Корреляционный анализ, построение корреляционных графов и плеяд. При построении корреляционной плеяды параметры изображаются при помощи геометрических фигур (например, кругов или прямоугольников), внутри которых записывается название параметра, а связи между параметрами – при помощи соединительных линий. Существует несколько правил построения корреляционных плеяд. 1. Поскольку в корреляционных исследованиях наличие взаимосвязи говорит лишь о сопряженности изучаемых параметров, но никак не о причинно-следственной зависимости, при построении корреляционных плеяд не рекомендуется использовать односторонние стрелочки, показывающие направление взаимосвязи. Используются либо двусторонние стрелки, либо простые соединительные линии. 2. Прямые и обратные взаимосвязи обозначаются (маркируются) посредством разных графических характеристик линий: например, прямые – сплошной линией, обратные – пунктирной. 3. Корреляционный анализ может включать достаточно большое количество параметров, между которыми могут быть получены самые разнообразные взаимосвязи. Чтобы рисунок, отражающий все эти взаимосвязи, был читаемым, важно удачно расположить элементы корреляционной плеяды относительно друг друга. Существующие различные варианты метода корреляционных плеяд являются в действительности несколько упрощенными эвристическими версиями более совершенных в математическом плане алгоритмов исследования структуры связей между компонентами многомерного параметра, использующими графы-деревья. Графы – это совокупность некоторых объектов, соединенных связями. Применительно к психологии корреляционные связи между психологическими показателями – это и есть графы. 26.Корреляционный анализ. Вычисление коэффициента корреляции в зависимости от типа эмпирических данных. Корреляционный анализ – статистический метод, позволяющий с использованием коэффициентов корреляции определить, существует ли зависимость между переменными и насколько она сильна. Коэффициент корреляции – двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных. В эмпирическом корреляционном исследовании контролируется порядок измерения переменных, т.е. план сбора данных зависит от исследователя. Установление корреляционных зависимостей Планы с двумя и более группами испытуемых Три основные формы контроля смешений с побочными переменными: 1. Стабилизация ПП или подбор уровней значений основных переменных таким образом, чтобы побочная переменная выступила в виде учитываемых уровней, задающих по существу факторный план ее взаимосвязей хотя бы с одной из двух измеряемых основных переменных (Подбор однородных групп) Составление однородных групп – это форма контроля различий в уровнях основной вариаты и стабилизации побочных переменных таким образом, чтобы на каждом уровне основной переменной их уровни также были представлены равномерно 2. Подбор пар. Эта стратегия подбора сравниваемых групп применяется в случаях, если исходное число испытуемых невелико. 3. Использование методики подбора контрастных групп приводит к тому, что заданное основной вариатой различие усиливается указанными сопутствующими переменными. · Использование средств статистического контроля, но не в значении замены экспериментального контроля проверкой статистических гипотез, а в значении замены управляющих воздействий – манипулирования переменными: попытками их более или менее полного охвата как уже существующих вариат. Основная цель использования мер связи в экспериментальном исследовании – проверка статистической нуль-гипотезы о том, что переменные Х и Y не связаны, т.е. имеют нулевой коэффициент корреляции в совокупности. При корреляционном подходе равноправными с точки зрения логики последующего содержательного вывода являются статистические решения о равенстве коэффициента корреляции какому-то числу, одинаковой корреляции переменной Х с другими переменными (Y и Z), значимости множественной корреляции. Традиционный подсчет коэффициента корреляции предполагает указание уровня значимости при определенном количестве наблюдений, т.е. числа измерений. Установление факта незначимости корреляции между переменными служит основанием для принятия решения отвергнуть гипотезу о связи между переменными. Интерпретация установленной связи полностью подчинена не следующему из самого эмпирического материала обоснованию ее направленности или опосредования ее тем или иным базисным процессом. |
