математические методы в психологии. мат.методы в психологии Ушакова А.И.. Федеральное государственное бюджетное образовательное учреждение высшего образования башкирский государственный педагогический университет им. М. Акмуллы
 Скачать 414.5 Kb.
|
|
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМ.М.АКМУЛЛЫ» Факультет психологии Кафедра общей и социальной психологии Направление03.03.01 Профиль «Социальная психология» Курс 2 ЗП-СПС-21-18 Ушакова Азалия Ильгизовна КОНТРОЛЬНАЯ РАБОТА по дисциплине «Математические методы в психологии» Проверил: Тулитбаева Галина Фанилевна преподаватель кафедры общей и социальной психологии Номер зачетной книжки: __91820463_______________________ Регистрационный номер ____4______________________ по журналу регистрации контрольных работ Дата представления______________________________ Оценка_________________________________________ подпись проверяющего Уфа – 2020 Вопросы к экзамену по математическим методам в психологии Особенности измерения в психологии. Измерительные шкалы. Измерение – приписывание числовых форм объектам\событиям в соответствии с определенными правилами. Это правило устанавливает соответствие между измеряемым свойством объекта и результатом измерения признака. Виды измерений: 1 Нормативное – результат испытуемого сравнивается с результатом других людей (эталонной группой лиц) 2 Критериальное - результат испытуемого сравнивается с каким-то критерием; определяется не относительный, а абсолютный статус 3 Ипсативное - результат испытуемого сравнивается с его предыдущим уровнем Проблема измерения в психологии связана с: -объектом измерения (человеком) - методами измерения (тест) - исследователем, испытателем, эксперементатором. Измерения в психологии — процедуры определения количественной выраженности психологических феноменов. В них применяются разнообразные шкалы, содержащие некое множество позиций, поставленных в некое соответствие с психологическими элементами. Разнообразные виды измерения в теоретическом плане формализуются с помощью понятий числового представления и шкалы. Числовое представление — это функция, гомоморфно отображающая эмпирическую систему с отношениями в числовую систему с отношениями. Шкалирование. Шкала измерения – форма фиксации результатов измерения с упорядочиванием их в определенную числовую систему. Шкала — это множество чисел, отношения между которыми отражают отношения между объектами эмпирической системы. В частности, шкалой можно назвать результаты измерения, полученные определенной системой вопросов, заданных испытуемому, а также сам инструмент измерения (т. е. систему вопросов, опросник, тест). Шкалы разделяют по типу в соответствии с тем, какие отношения они отражают, и, что эквивалентно, теми допустимыми (математическими) преобразованиями, которые оставляют инвариантными соответствующие отношения. Классификация шкал измерения (С. Стивенс). А)неметрические измерительные шкалы Номинативная шкала (неметрическая), или шкала наименований - это шкала, классифицирующая по названию (лат. nomen - имя, название). В её основе лежит процедура, обычно не ассоциируемая с измерением. Пользуясь определённым правилом, объекты группируются по различным классам так, чтобы внутри класса они были идентичны по измеряемому свойству. Затем каждому объекту присваивается соответствующее обозначение. Простейший случай номинативной шкалы - дихотомическая шкала, состоящая всего лишь из двух ячеек, например: «имеет братьев и сестер - единственный ребенок в семье»; «иностранец – соотечественник»; проголосовал «за» - проголосовал «против» и т.п. Примером шкалы такого рода может служить классификация испытуемых на мужчин и женщин Порядковая шкала, или ранговая шкала - это шкала, классифицирующая по принципу «больше – меньше» (в соответствии с возрастанием или убыванием значений общего для этих объектов признака). Как следует из названия, измерение в этой шкале предполагает приписывание объектам чисел в зависимости от степени выраженности измеряемого свойства. Если в шкале наименований было безразлично, в каком порядке мы расположим классификационные ячейки, то в порядковой шкале они образуют последовательность от ячейки «самое малое значение» к ячейке «самое большое значение» (или наоборот). Б)метрические измерительные шкалы. Интервальная шкала – произвольно выбирается нулевая точка (не значит, что свойство полностью отсутствует) и единица измерения; это шкала, классифицирующая по принципу «больше на определенное количество единиц - меньше на определенное количество единиц». Наиболее распространенный пример использования интервальной шкалы — психологические тесты личности, установок и способностей. Шкала равных отношений или абсолютная шкала – характеризуется тем, что нулевая точка зафиксирована и обозначает полное отсутствие признака; это шкала, классифицирующая объекты или субъектов пропорционально степени выраженности измеряемого свойства. Пример любые признаки, значения которых получается при счете (количество выборов, ошибок) 1. Дихотомическая классификация часто рассматривается как вариант шкалы наименований. Это верно, за исключением одного случая, когда мы измеряем свойство, имеющее всего лишь два уровня выраженности: «есть—нет», так называемое «точечное» свойство. Примеров таких свойств много: наличие или отсутствие у испытуемого какой-либо наследственной болезни (дальтонизм, болезнь Дауна, гемофилия и др.), абсолютного слуха и др. В этом случае исследователь имеет право проводить «оцифровку» данных, присваивая каждому из типов цифру «1» или «0», и работать с ними как со значениями шкалы интервалов. Первичный анализ и представление данных эмпирического исследования. В процессе анализа и обработки эмпирических данных обычно используются такие термины как “признак”, “показатель”, “параметр”, “переменная”. Употребляются они чаще всего как синонимы. Другой смысл имеет термин “значение”. Значение - это определенная числовая величина того или иного показателя, выявленная у конкретного испытуемого (Куликов, 2001). Обработка полученных эмпирических данных начинается обычно с первичного анализа переменных. Для большей наглядности изображения они заносятся в таблицы или изображаются в виде графиков. Проверка точности выполнения этой части работы обеспечивает достоверность дальнейшей обработки и анализа результатов исследования. Использование методов математической статистики при обработке первичных эмпирических данных необходимо для повышения достоверности выводов, как в научном, так и в практическом психологическом исследовании. Начинает исследователь обычно с анализа первичных статистик. Важнейшими среди них являются: 1. средняя арифметическая 2. мода 3. медиана 4. разброс 5. дисперсия 6. среднее квадратичное отклонение. Типичными задачами математической обработки данных являются: 1. оценка достоверности различий, 2. корреляционный анализ, 3. факторный анализ, 4. анализ изменчивости признаков. 1. Во многих исследованиях осуществляется поиск различий в психологических показателях у испытуемых, характеризующихся разными особенностями. Для обработки соответствующих данных могут использоваться критерии на выявлении различий в уровне исследуемого признака или в распределении признака. 2. Во многих исследованиях осуществляется поиск взаимосвязи психологических показателей у одних и тех же испытуемых. Для обработки соответствующих данных могут использоваться коэффициенты корреляции. 3. Для выявления структуры данных (и соответственно структуры изучаемой психологической реальности), а также взаимосвязи данных, используется факторный анализ. 4. Во многих исследованиях интерес представляет анализ изменчивости признака под влиянием каких-либо контролируемых факторов, или другими словами, оценка влияния разных факторов на изучаемый признак. Во психологических исследованиях может выявляться значимость изменений (сдвига) каких-либо психологических, поведенческих параметров и проявлений за определенный промежуток времени, в определенных условиях (например, в условиях коррекционного воздействия). Формирующие эксперименты в практической психологии решают именно эту задачу. Для обработки соответствующих данных могут использоваться коэффициенты для оценки достоверности сдвига в значениях исследуемого признака. Для выбора статистических критериев и знакомства с основами их применения для обработки эмпирических данных можно использовать ряд пособий. Каждый исследователь предпочитает статистические критерии, исходя из типа задачи и вида данных, которые подлежат обработке. При выборе математико-статистического критерия нужно, прежде всего, идентифицировать тип переменных (признаков) и шкалу, которая использовалась при измерении психологических показателей и других переменных – например, возраст, состав семьи, уровень образования. В качестве переменных могут выступать любые показатели, которые можно сравнивать друг с другом (то есть измерять). Это может быть время выполнения задания, количество ошибок, уровень самооценки, количество правильно решенных задач и качественные особенности их выполнения, личностные показатели, получаемые в психологических тестах, и другие. В области практической психологии широко используются номинативные и порядковые шкалы. Речевые высказывания клиента, виды поведенческих реакций, улыбки, взгляды, – все это может рассматриваться в качестве переменных. Главное - иметь четкие и ясные критерии их отнесения к тому или иному типу в зависимости от поставленных гипотез и задач. 3.Наглядное представление данных эмпирического исследования. В наглядной форме Табличный способ позволяет представить качественные и количественные данные с кратким сопроводительным объясняющим текстом. Таким текстом служат название таблицы, раскрывающее связь между числовыми рядами, и внутренние заголовки таблицы (указывающие измеряемые признаки, место, время, единицы измерения и т. п.). Графики более наглядно, чем таблицы, отображают изменение экспериментальных данных. Графики строятся в прямоугольной системе координат, в которой на оси «X» отмечается значение выборки, а по оси «Y» — значение, порядок признака, частота события. Виды графиков 1. Линейный график–передает изменения в некоторых мерных числах, например, изменение средних оценок контрольных работ, проведенных в одном классе в течение учебного года. 2. Гистограмма позволяет наглядно представить распределение первичных данных. Графическое представление распределения различных значений с учетом их частот называют столбиковой диаграммой. Подобную группировку используют лишь для качественных данных, четко разделяющихся на обособленные категории. Количественные данные всегда располагаются на непрерывной шкале и, как правило, весьма многочисленны. Поэтому, такие данные предпочитают группировать по классам, чтобы яснее видна была основная тенденция распределения. Группировка состоит в основном в том, что объединяют данные с одинаковыми или близкими значениями в классы и определяют частоту для каждого класса. Способ разбиения на классы зависит от того, что именно экспериментатор хочет выявить при разделении измерительной шкалы на равные интервалы. Данные, разбитые на классы по непрерывной шкале, нельзя представить графически так, как это сделано выше. Поэтому предпочитают использовать так называемые гистограммы - способ графического представления в виде примыкающих друг к другу прямоугольников. Полигон частот отличается от гистограммы тем, что в полигоне частота интервала сведена к его центру, а при гистограмме частоты изображают равномерно в пределах всего интервала. Для того, чтобы построить полигон частот (распределения) на пересечении градации признака (или середины каждого интервала) и соответствующей частоты ставится точка, затем эти точки соединяются отрезками прямой линии. Рекомендуется использовать не менее 5, но не более 13 градаций. 4. Кумулятивный график частоты (накопляющее распределение частоты) – частота отдельных интервалов совокупности рассматривается кумулятивно, то есть к частоте каждого последующего интервала прибавляются частоты всех предыдущих интервалов. 5. Диаграммы сопоставляют количественную информацию в виде площадей различных фигур (круг, прямоугольник, сектор, цилиндр, и др.). 4.Нормальное теоретическое распределение. Свойства нормального теоретического распределения. Понятие статистической нормы Кривую нормального закона распределения называют нормальной или гауссовой кривой. Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. во Франции, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции.  где u – высота кривой прямо над всяким заданным значением х на графике распределения частот; е– основание системы натуральных логарифмов = 2,718.., а и s- числа, которые определяют положение кривой относительно числовой оси и регулируют ее размах. График нормального распределения представляет собой так называемую колоколообразную симметричную кривую. Меняя значения а и s, можно сдвигать конкретную нормальную кривую по числовой оси вверх и вниз и менять ее размах. Величина a соответствует среднему распределения частот большой выборки (математическому ожиданию); s - стандартному отклонению этого распределения. Таким образом, параметр а (математическое ожидание) характеризует положение, а параметр s2 (дисперсия) – форму нормальной кривой. Нормальный закон распределения случайной величины с параметрами а=0, s2=1, т.е. N(0;1), называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной. Площадь ограниченная такой кривой равна = 1. Для совмещения любой нормальной кривой с единичной достаточно выполнить простое преобразование исходного распределения путем вычитания среднего значения  из каждого индивидуального балла Хi и деления на s. , z = 0, s=1.Нормальное распределение характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения близкие к средней величине - достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречается в естественно - научных исследованиях и казалось «нормой» всякого массового случайного проявления признака. Нормальная кривая всегда будет симметричной относительно а. Площадь между кривой и осью х равна 1. Свойства нормального теоретического распределения 1) мода, медиана и среднее арифметическое равны или имеют близкие по величине значения; 2) показатели асимметрии и эксцесса равны нулю, As=0 и Еs=0. 3) Выполняется правило трех сигм. Правило трех сигм Общее для всех этих кривых: в любом нормальном распределении приблизительно: 1. 68% площади под кривой лежит в пределах одной s от среднего в любом направлении (то есть а ±1s ); 2. 95% площади под кривой лежит в пределах двух s от среднего в любом направлении (то есть а±2s ); 3. 99,7% площади под кривой лежит в пределах трех s от среднего в любом направлении (то есть а ±3s ). Правило трех сигм на языке теории вероятностей: P{÷X-mê P{÷X-mê<2s} = F (2) = 0.9545 P{÷X-mê<3s} = F (3) = 0.9973 Вероятность того, что число Х попадает в интервал |X-mê Статистическая норма – среднестатистический показатель какой-либо величины. Люди отличаются друг от друга рядом свойств и качеств. Большинство показателей тяготеют к среднестатистической норме, но не совпадают с ней. 5.Критерии, используемые при анализе выборок на принадлежность нормальному закону распределения случайной величины. Критериями для сравнения выборок служат: равенство двух выборочных дисперсий, равенство двух выборочных средних и однородность ряда выборочных дисперсий. Критерий однородности ряда дисперсий. Однородность дисперсий ошибок измерений случайной величины в случае равного объема выборок оценивают по критерию Кохрена, расчетное значение которого определяют по формуле  ,где  - дисперсия ошибок измерения СВ - й выборки; - число выборок.Критическое значение критерия определяют по таблице (приложение 1) при заданных значениях уровня значимости  и степенях свободы: ; , где - число измерений (объем выборки).Критерий равенства двух дисперсий. Для сравнения дисперсий двух выборок используют 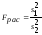 - критерий Фишера. Определяют расчетное значение - критерия в виде отношения большей дисперсии к меньшей .Так как проверяется гипотеза о равенстве генеральных дисперсий, то желательно, чтобы это отношение было как можно ближе к единице. Критическое значение - критерия вычисляем с помощью статистической функции РАСПОБР. Число степеней свободы принимают соответственно , где - объем выборки. Гипотеза о равенстве дисперсий подтверждается, если .Критерий равенства двух средних. Для сравнения двух выборочных средних используют  - статистику. После проверки гипотезы о равенстве двух выборочных дисперсий, вычисляют общую дисперсию двух выборок и расчетное значение - статистики по формулам:  .Критическое значение - статистики определяем с помощью статистической функции СТЬЮДРАСПОБР. Число степеней свободы . Гипотеза о равенстве средних значений подтверждается, если .6.Вычисление и смысл мер центральной тенденции (мода, медиана, среднее арифметическое). Меры центральной тенденции (measures of central tendency) — способы осмысления центральной или средней позиции множества наблюдений, оценок, группы чисел и т.д. На практике существуют большое разнообразие мер центральной тенденции (например, взвешенное, винсоризованное, гармоническое, геометрическое средние, среднее Колмогорова и др), но чаще всего встречаются: мода; среднее арифметическое; медиана. |